大规模时序图中持续性稠密子图搜索算法研究
李 源,刘金生,赵会群,孙 晶
北方工业大学 信息学院,北京 100144
时序图是一个随时间不断变化的图结构,其中边上的时间戳代表该边出现的时间。这一模型具有很多现实应用。例如,社交网络[1-2]、作家协作网络[3]、生物信息网络[4]等。稠密子图挖掘问题(cohesive subgraph mining,CSM)作为图计算的基础研究问题之一,近几年被越来越多的学者在时序图上进行深入研究。一般来讲,CSM分为不考虑查询节点的稠密子图检测问题(cohesive subgraph detection,CSD)和考虑查询节点的稠密子图搜索问题(cohesive subgraph search,CSS)两类。时序图上的CSD问题已经被学者们广泛研究。但是,当时序图规模过大时,发现时序图中所有的稠密子图将变得不切实际。为此,本文将主要研究在时序图中长期被忽视的CSS问题。该问题的描述如下:给定一个特定的查询节点,找到包含该查询节点,且满足一定时间和结构约束条件的子图。由于查询节点的引入,这一问题将具有更强的现实意义。
在真实的时序网络中找到在一段时间内持续出现的稠密子图通常是很有意义的[5]。为此,本研究采用(θ,τ)持续性k-核子图模型。其中,参数θ表示判定持续性的最大间隔。即,将连续出现两次时间间隔小于θ的子图视为不间断的。参数τ用于表示最短持续时间约束,即子图不间断的时间至少应为τ。参数k用于结果子图的结构约束,即子图中所有节点都至少有k个邻居。从后文实验可以看出,参数θ和τ根据实际应用场景而变化。当时序图变化较为频繁时,θ应取值较小;当时序图变化不频繁时,θ取值可以适当增大。τ值可以根据实际需要定义,一般来说,τ值较大时,问题的时间约束更加严格,查询结果个数会更少。本文将研究大规模时序图中,找到一个包含特定查询节点且满足该模型的时序子图。例如,图1中包含两个(2,3)持续性3-核子图,分别是H0={v0,v1,v2,v3}和H1={v0,v4,v5,v6}。
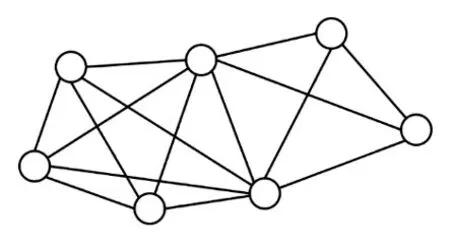
图1 一个时序图的实例Fig.1 Example of temporal graph
本研究首先证明了时序图中查询(θ,τ)持续性k-核子图是NP-难问题。为解决这一问题,本文提出通过全局和局部两种思路设计的算法,分别命名为S-Global和S-Center算法。其中S-Global算法从全局角度出发,不断删除不满足条件的节点,最后得到一个极大的(θ,τ)持续性k-核图。在此过程中,将通过提出的削减规则减少搜索空间。另一个算法S-Center从查询节点出发,以查询节点为中心将其他节点分层,不断地在候选结果的邻接点中找到正确的节点加入子图,直到找到目标结果。这种方式的优点是无需遍历整个时序图。在四个真实世界网络中的大量实验,验证了提出算法的高效性。其中S-Global算法更适用于时序图较为稠密的场景,而S-Center算法则适用于稀疏图场景。
1 相关工作
时序图上的稠密子图检测问题已经被学者们广泛研究。吴欢欢等人提出了一种时序图上的(k,h)-核模型,即子图中每个顶点至少有k个邻接点和h条时序边[6]。马帅等人提出一种算法,在加权时序图中通过时间快照计算权值找到一个时间段内的密集连接子图[7]。瑟莫兹团队的工作是在时序图的所有时间快照上找到一个持久的密集子图[8]。黄欣等人基于k-truss模型,提出了一种基于TCP索引找到包含最大k的查询顶点的k-truss的方法[9]。
在不同类型的图结构中,稠密子图的搜索问题同样已经被深入研究。例如,基于静态属性图中,文献[10]提出了一种基于k-核的方法,以找到包含查询节点的稠密子图。在加权的属性图中,文献[11]提出了一种方法来找到权值较高的内聚子图。在地理社交网络中,文献[12]提出了一种基于位置信息找到图中稠密子图的方法。然而,时序图中稠密子图搜索问题则尚未被充分研究。
2 问题定义及相关概念
本文用G(V,E)表示一个无向时序图。其中,V和E分别代表节点集和边集。用n=|V|和m=|E|分别表示节点数量和边的数量。每一条时序边e∈E是一个三元组(u,v,t)。其中u和v都是V中的节点,并在t时刻上产生联系。这里假设所有时间都是整数。注意,若t i≠t j,(u,v,t i)和(u,v,t j)将会是两条不同的时序边。对于V的一个子集S,用G[S]表示它的诱导子图,且E(S)={(u,v,t)|u,v∈S,(u,v,t)∈E}表示G[]S中的边集。用N G(u)={(v,t)|(u,v,t)∈E}表示u在G中的时序邻居集合。最后,用G′(V′,E′,T C)来表示一个时序图G在一个时间段T C=[t i,t j]的静态投影图。例如图2是图1在时间段[4,6]上的静态投影图。
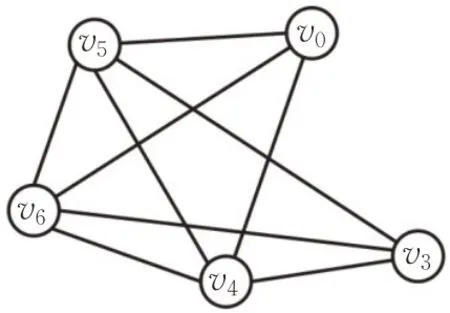
图2 图1在[4,6]上的静态投影图Fig.2 Static projection of Fig.1 in[4,6]
2.1 滑动窗口模型的使用
在静态图中,k-核图通常是结构内聚的。其中,每个节点都至少有k个邻居[13-15]。在时序图中,这种内聚子图通常需要持续存在一段时间才是有意义的。本研究中用(θ,τ)持续性k-核图定义时序图中的一个持续出现的内聚子图,并用滑动窗口模型找到这种内聚子图。其中θ将作为滑动窗口的长度。τ将成为一个时序子图通过滑动窗口计算的最小有效寿命,后文中会有详细定义。接下来将给出在滑动窗口模型的基础上一个节点的有效寿命定义。
定义1(节点有效寿命)给定一个时序图G(V,E),节点u∈V,参数θ,k。节点u的有效寿命被定义为:当u的度数在θ长度的滑动窗口内大于k时,滑动窗口的移动覆盖区间。
例如,当核数k=3,滑动窗口长度θ=2时,v3的在整个时序图中有效寿命有三段,分别是[0,2]、[4,6]和[9,14]。即滑动窗口在这些时间区内滑动时,v3在滑动窗口内的度数都大于3。
由于在实际应用中,相同时间长度的情况下,连续不断的有效寿命比断断续续的有效寿命更加具有实际意义。所以在本研究中重新定义一个节点的有效寿命长度。
定义2(节点有效寿命长度)时序图G中的一个节点u通过θ长度的滑动窗口得到的有效寿命后,其长度δG(u)的计算方式为:
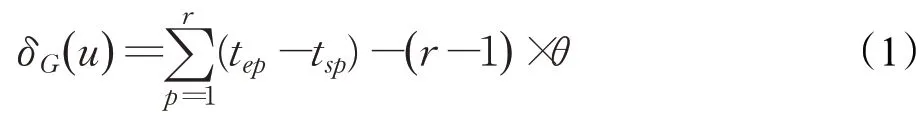
其中,r表示节点u的有效寿命中不连续的极大有效寿命段的数量,t sp、t ep分别表示第p个极大有效寿命段的开始和结束时间。例如图1中,当k=3,θ=2时,v3在整个时序图内的有效寿命δG(v)3=(2-0)+(6-4)+(14-9)-2×2=5。
值得注意的是,当时序图结构发生改变时,一个节点的有效寿命及寿命长度也要随之改变。例如图1中,若只考虑子图H0={v0,v1,v2,v3},则节点v3的寿命将变为两段,分别是[0,2]和[9,14]。其有效寿命δH0(v)3=(2-0)+(14-9)-1×2=5。
2.2 问题定义及分析
接下来基于以上定义,将给出(θ,τ)持续性k-核图模型的定义和本研究的问题定义。
定义3((θ,τ)持续性k-核图)给定一个时序图G(V,E),参数θ、τ、k。在θ长度的滑动窗口模型中,若对于∀v∈V,δG(u)>τ,则G是一个(θ,τ)持续性k-核图。
定义4((θ,τ)持续性k-核子图搜索问题)给定一个时序图G(V,E),参数θ、τ、k和一个查询节点q。找到一个G中的一个诱导子图G[]S满足如下条件:(1)q∈S。(2)G[]S是一个(θ,τ)持续性k-核图。(3)G[S]不会被其他满足条件(1)和(2)的诱导子图完全包含。
接下来,定理1证明了(θ,τ)持续性k-核图搜索问题为NP-难的。
定理1时序图中包含查询节点的(θ,τ)持续性k-核图搜索问题是一个NP-难问题。
证明 此处可将(θ,τ)持续性k-核子图搜索问题转化为包含查询节点的子图检测问题。在得到一个时序图G之后,新建一个虚拟节点q作为查询节点。令q与图G中所有节点在G中出现的每一个时间戳上都有一条时序边相连,将这个新构造的虚拟图(G∪q)记为G*。根据构造条件,G*中的任何(θ,τ)持续性k-核子图都包含q,因此G*上的搜索问题就转化为G中(θ,τ)持续性k-核图检测问题,而这一问题已经被证明是NP-难的[6],所以本研究的问题同样是NP-难的。
3 搜索算法
在搜索算法开始之前,需要对时序图进行预处理以对时序图进行初步削减,随后在削减后的时序图中进行搜索算法找到目标子图。首先通过滑动窗口模型算法构建一个θ长度的窗口,并令其在时序图的时间戳范围内滑动,以窗口右端作为窗口的位置,记录滑动窗口在每一个时间戳上,每一个节点在窗口内的度数,以此构成一个度数时序矩阵J。其中J[i][j]表示节点v i在滑动窗口走到时间戳t=j时的度数。在得到查询节点q,参数k、θ、τ之后,可以通过矩阵J,得出所有节点的有效寿命,删除那些与查询节点的寿命交集小于τ的节点,将剩余节点计入候选节点集Ca,Ca中将可能包含一个(θ,τ)持续性k-核图。接下来,本章中提出两种基于枚举的算法找到这个子图。
3.1 S-Global算法
在预处理部分得到候选节点集Ca之后,本算法从全局的角度出发,即从所有候选节点与查询节点构成的子图开始,在每一次的枚举中找出一个待删除的节点集合,然后判断剩余的节点集合能否构成一个符合要求的结果。
算法1是本算法的详细细节。其中R是最终要找到的极大结果子图集合,De是每次枚举过程中要删除的节点集合,Safe是安全节点集合(第1行)。当得到一个候选节点集之后首先将Ca中的所有节点按其静态投影度数排序(第2行)。在第一次递归中需要判断Ca是否满足(θ,τ)持续性k-核图的条件,若满足,则Ca构成的诱导子图就是图G中的极大结果(第3行)。若不满足,则进入之后的递归操作。每一次按照顺序将一个节点u加入进De准备删除(第5行),对于剩余的子图,先判断其有效寿命是否大于τ(第6行),若大于τ,则这个子图中的极大k-核图就是一个极大结果,将其代入R并停止递归(第12行)。否则,继续向后按顺序对u之后的节点进行递归判断(第17行)。当一个节点完成递归之后,保留这个节点作为安全节点进入节点集Safe(第18行)。注意,每次更新子图时都要对度数时序矩阵J进行更新(第11和19行)所有递归判断完成后,将R内的所有子图输出作为结果(第4行)。

为了减少枚举,也就是递归判断的次数,本算法中使用了三个枚举约简规则:
规则1当枚举到一个节点u时,若剩余子图的有效寿命已经大于τ,则无需枚举u之后的节点。
规则2当枚举到一个节点u时,如果存在某个Safe中的节点不满足k-核条件,则本次枚举失效。
规则3在枚举一个节点u之前,若Safe集合构成的子图寿命小于τ,则u及u之后的节点都无需枚举。
以图1为例,假设q=v0,θ=2,τ=5,k=3,最初Safe={v0},Ca={v2,v3,v6,v1,v4,v5}。显然q与Ca内的节点不能直接构成一个(θ,τ)持续性k-核图。将v2加入De。此时由于G[Ca/De]的有效寿命小于τ,根据枚举约简规则1继续将Ca内v2后面的节点加入De中,直到De={v6,v4,v5},Ca/De={v2,v3,v1}。此时G[Ca/De]的有效寿命为[0,2]∪[9,14],有效寿命长度是6,大于τ,与此同时,G[(Ca/De)∪q]的静态投影是一个k-核图,则将这个子图保存至R中。当所有枚举操作完成后,得到本例的唯一结果子图{v2,v3,v1,v0}。
由于本算法涉及到枚举操作,枚举Ca中节点的所有组合,所以本算法的时间复杂度为O(2nCa),n Ca是Ca中的节点个数。但由于枚举约简规则的存在,算法的实际运行时间将远远小于2n Ca。
3.2 S-Center算法
在S-Global算法中,由于需要遍历整个Ca构成的子图,当Ca内节点数量较多时,这一枚举算法将产生较大的时间开销。本节中提出的S-Center算法将从查询节点出发,每次枚举其邻域中的一个节点进入子图,直到找到一个极大的(θ,τ)持续性k-核图。在进行该算法之前,首先要将Ca中的所有节点进行分层,令查询节点在第0层,其余所有节点的层数是其到查询节点的最短距离。随后在算法中,与S-Global中的枚举方式类似,在对Ca中的节点排序之后,每一次枚举一个节点进入待查子图中,但不同的是,在一个节点进入子图后,随后枚举的节点只有这个节点下一层的节点与同层该节点之后的其他节点。
算法2描述了S-Center算法的详细过程。此处用到的两个集合分别是结果子图集合R和当前的待查子图节点集Sub(第1行)。在得到候选节点集Ca后,为节点分层并排序,同时记录每一层中节点个数(第2~4行),然后开始在q的邻域中进行枚举(第5、6行)。在每一次枚举操作中,如果当前枚举的节点u加入子图后子图的有效寿命仍然大于τ,则这个节点可以加入Sub中(第8、9行)。此时若G[Sub]的静态投影是一个k-核图,则说明G[ ]Sub是一个(θ,τ)持续性k-核图。更新R中的结果以维护极大结果集合(第10~13行)。然后继续进行枚举操作(第14~20行)。


在枚举过程中,同样有3个枚举约简规则来减少枚举操作的次数:
规则4当枚举到一个节点u时,若这个节点进入待查子图后子图的有效寿命小于τ,则节点u无需加入子图。
规则5当一个节点v加入待查子图后,如果子图中存在一个与v隔层的节点度数仍然小于k,则本次枚举失效。
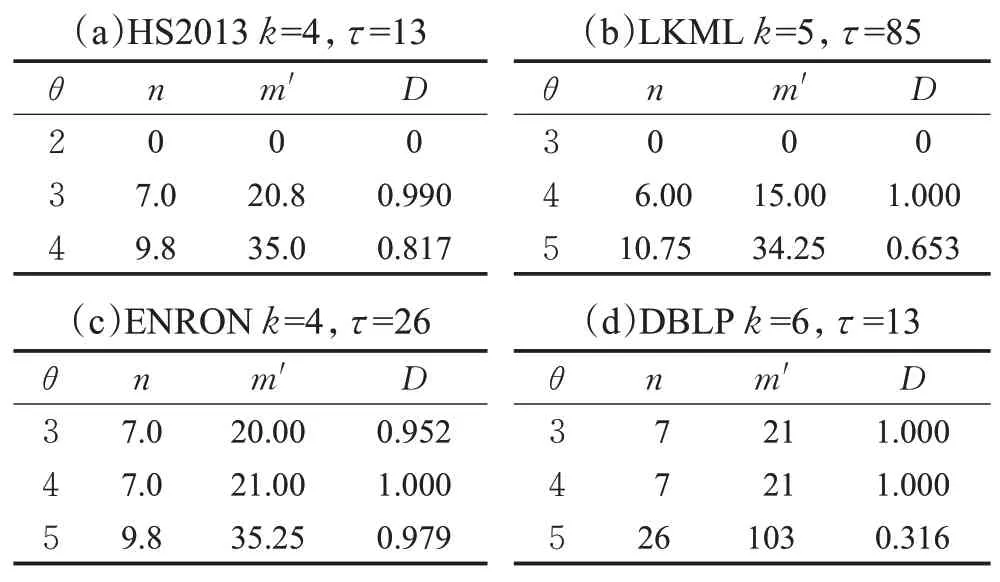
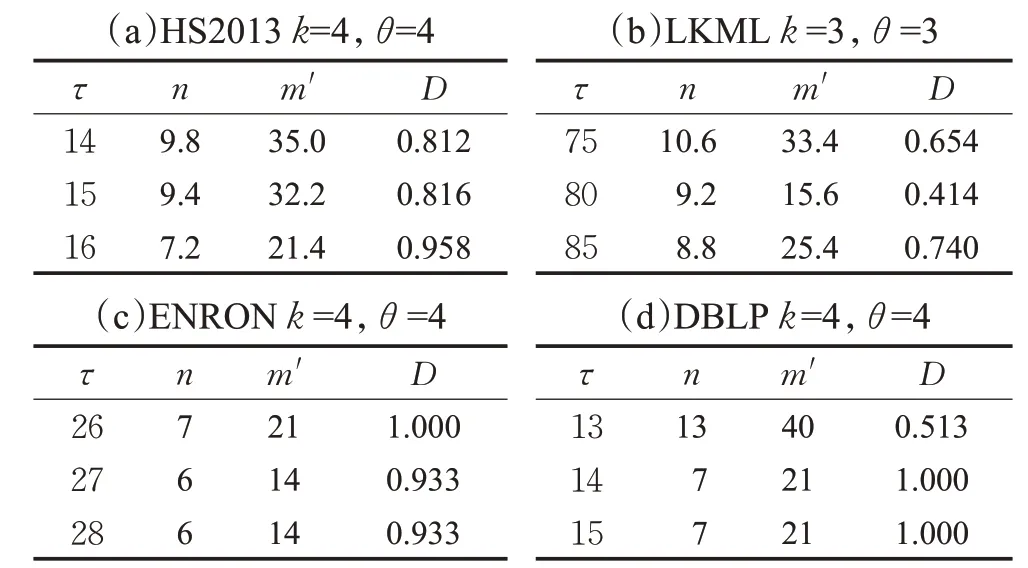
规则6当枚举到一个节点v时,记m′为当前子图中v上一层节点的最小度数,n′为与v同层节点中未进入子图的数量。若m′+n′ 同样,以图1为例,假设q=v0,θ=2,τ=5,k=3,由于图中所有节点都在同一层中,所以Ca={v2,v3,v6,v1,v4,v5}。最初待查子图内只有v0,寿命为[0,7]∪[9,14]。然后将v2加入子图,寿命为[0,3]∪[7,14]。下一次将v3加入子图,此时寿命为[0,3]∪[9,14],下一次枚举的节点v6加入子图之后寿命长度小于5。根据枚举约简规则4,v6节点无需进入子图。然后将下一个节点v1加入子图。此时子图内的节点{v2,v3,v1,v0}。能构成一个(2,5)持续性3-核图,将其记录进入R。当所有枚举操作完成后,得出唯一的极大结果{v2,v3,v1,v0}。 由于S-Center同样是一个基于枚举的算法,所以这个算法的时间复杂度依然是O(2nCa),但由于三个枚举约简规则的存在,这个算法的实际运行时间同样远远小于2nCa。而且S-Center无需全局遍历Ca中的所有节点,这进一步的提高了效率。 在本算法中,每次递归都从待查子图的邻域中枚举一个节点,并且找到一个查询结果后,算法不会停止,而是继续进行递归操作找到一个极大结果。因此在不考虑约简规则的情况下,这一算法始终可以找到一个精确的极大结果。而约简规则只会删除那些一定不在查询结果的枚举集合。所以S-Center算法在查询节点有效时,始终可以找到一个精确的极大结果。 本节中给出两种算法的时间复杂度。两种算法都采用了枚举的思路,对于S-Global算法来说,每次枚举的节点是要删除的节点集合,而候选节点中剩余的节点作为待查子图。那么当待查子图内节点数小于k+1时,这个子图一定不会是查询结果,则这一算法的实际运行时间复杂度为:显然,当候选子图G[ ]Ca与结果子图相差不多时,这一算法将更快地得到结果。该种情况一般在查询节点有效寿命较长,时序图更加稠密时发生。对于S-Center算法来说,算法中枚举的节点集的诱导子图本身就是待查子图。显然,这一算法的时间复杂度与G[Ca]内节点的层数有关。当G[Ca]内所有节点的层数相同时,枚举算法将会遍历候选字图中的所有节点,其最坏时间复杂度为O(2nCa)。当节点分层较多时,由于枚举到某一节点时,隔层以上的节点将不会被枚举。假设候选节点集共分为s层,则此时算法的实际时间复杂度为。其中N i是G[Ca]第i层节点的数量。显然,当G[Ca]分层较多时,这一算法将更快得到结果。该种情况一般出现于查询节点有效寿命较短,时序图较为稀疏的条件下。 本章中通过一些真实的数据源验证算法的有效性及运行效率,并通过一些对比实验说明参数对算法性能的影响。两种算法都由C++编写,运行环境为Windows Server 2012 R2操作系统,Inter®Xeon®Platinum 8163,2.49 GHz CPU和16 GB内存。 本文中取4个不同的真实世界的时序图数据源进行研究。数据源的详细情况见表1。其中,|V|、|E|、|E′|、|T|和dmax分别是时序图中的节点数,时序边数,静态投影边数,时间戳范围和节点的最大静态投影度数。HS2013是从sociopatterns网站上下载的面对面交互网络,时间戳单位为h。LKML和ENRON是从konect网站上下载的时序社交网络,单位是月。DBLP是DBLP计算机科学文献库中的作家协作网络,单位是年。 表1 时序图数据集的参数Table 1 Parameters of temporal graph datasets 本文中的两个算法都涉及到了三个参数θ、τ、k。其中θ、τ作为时序参数用于确定滑动窗口的长度和子图的最短持续时间,k用于确定子图的结构内聚性。本文中的实验部分将每个数据源需要的3个参数各变化3次,且每一组参数都取5个不同的查询节点进行5次实验,并记录其运行结果的平均值作为实验结果。具体的取值情况如表2所示。 表2 不同数据源上的实验参数Table 2 Experimental parameters in different datasets 本节中固定每组数据源的参数k,然后分别固定参数θ和τ并改变另一个参数,以确定这两个参数对算法性能的影响。图3中的4幅图为变化参数θ时两种算法及预处理过程在4个数据源上的运行时间。通过这4幅图可以得出,当θ越大时,算法的运行时间越长。这是因为当θ变大时,同一条时序边会计入更多的滑动窗口中。图4的4幅图为变化参数τ时两种算法在4个数据源上的运行时间。由于当τ变大时,更多的时序边不满足有效寿命的约束条件,所以算法的运行时间会变短。值得一提的是,S-global算法有时会出现运行速度过小的情况,例如图3(d)、图4(b)和图4(d)。这是因为有些时候G[Ca]本身就能构成一个(θ,τ)持续性k-核图,在S-Global算法中无需进行更多的枚举操作,这大大降低了算法的运行时间。 图3 变化参数θ时的运行时间Fig.3 Run time when varyingθ 图4 变化参数τ时的运行时间Fig.4 Run time when varyingτ 本实验中将固定θ、τ,改变参数k并观察其对算法运行时间的影响。图5显示了本实验的结果。实验结果表明,k值变大时,两个算法的运行时间都变短。这是因为,当k值变大时,满足结构约束的节点变得更少,也就是说,候选节点集Ca中的节点边更少。同时实验中发现,算法的运行时间与Ca的规模与结果子图规模的关系密切相关,当Ca规模与结果子图规模相差较大时,S-Center的运行速度较快,反之,S-Global的运行速度较快。 图5 变化参数k时程序的运行时间Fig.5 Run time when varying k 本实验记录了两种算法在运行过程中枚举操作的执行次数,同时记录了不同参数下每组实验的候选节点集Ca的情况,以此可以估算出不考虑枚举削减规则时的预计枚举次数。表3展示了本次实验的详细结果。其中n Ca表示候选节点集Ca的节点个数,l Ca表示候选节点集的分层数,PGlobal、PCenter分别表示S-Global算法和S-Center算法运行时的枚举次数。从表中可以看出,两种算法中的枚举削减规则都能够极大地减少枚举次数。在Ca与查询结果非常接近时,S-Global算法的枚举次数将大幅减少,反之,Ca与查询结果相差较大时,S-Center算法更具优势。 表3 枚举次数统计Table 3 Statistics of enumeration times 本实验考察了两种算法在4个数据集上的内存开销情况。表4记录了本实验中不同数据源在不同参数情况下的平均内存开销。表内的第一列为数据源本身占用的内存大小。从结果中可以看出,两种算法的内存开销几乎相同,原因是两种算法均采用了基于深度优先包含枚举的策略。同时,发现两种算法参数变化对内存开销影响较小,原因是(1)在不同参数下,经过预处理后得到的候选节点集Ca的规模通常很小,该结论能够通过表3中的n Ca数量得到验证。(2)由于两种算法均采用基于深度优先的枚举策略,在搜索过程中只需保存枚举中当前搜索分支的中间结果,而且由于两种算法均采用了削减规则,树中搜索分支不会过深。为此,即使n Ca大小有所不同,内存开销影响也不大。因此从理论上证明两种算法参数变化几乎不影响内存开销。多次不同的实验也验证了该结论。此外,ENORN数据源上的内存开销远远大于其数据源,因为ENORN数据源的时间戳范围跨度很大。 表4 不同数据源上的内存开销Table 4 Memory overhead on different datasets MB 本实验中将固定每组数据源的k值,然后分别固定参数θ和τ并改变另一个参数,以记录时间约束对结果质量的影响。对于每一组实验得到的结果子图,用一个系数表示子图的稠密程度。其中m′表示子图内的静态边数,n表示子图内的节点数。显然D值越大,结果子图越稠密。表5中的4张表展示了参数θ对查询结果的影响。可以看出,θ的大小与结果内子图的节点数量和边数量都呈正相关,因为同一条边会被包含在更多的滑动窗口中,节点的有效寿命会变长。但当子图内节点数量突然增多时,子图的密度会有所降低。因为两种算法都旨在找到数据源中的极大结果,且k值是固定的。表6中的4张子表展示了参数τ对查询结果的影响。显然,τ的大小与结果内子图的节点数量和边数量都呈负相关,且与表4结论类似,子图内节点数量突然减少时,子图的密度会有所增加。 表5 参数θ对查询结果的影响Table 5 Effect of parameterθon query results 表6 参数τ对查询结果的影响Table 6 Effect of parameterτon query results 本文研究了时序图中的稠密子图搜索这一新颖的问题。本研究利用(θ,τ)持续性k-核子图这一模型定义了时序图中的一种稠密子图概念,在去除干扰节点后的候选节点集,也就是削减后的时序图中,设计了两种算法,从两种不同的角度枚举这个时序图中的节点集合,来找出能够组成一个(θ,τ)持续性k-核图的极大节点集作为搜索结果。在枚举过程中,通过一些高效的削减规则来大幅度减少枚举的执行次数增强算法的效率。最后,本文通过实验在四个时序图中验证了提出算法的高效性和有效性,并给出了两种算法应用于不同场景的建议。3.3 两种搜索算法的比较
4 实验
4.1 数据集

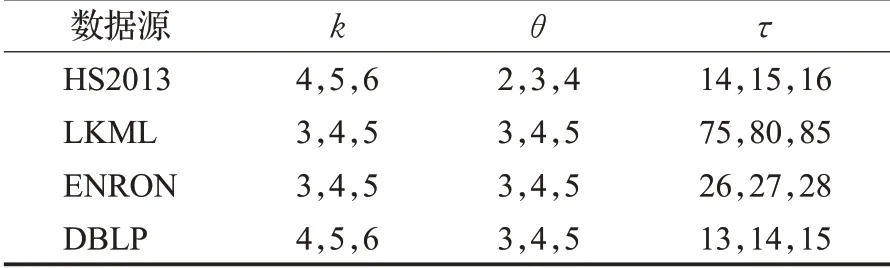
4.2 参数设定
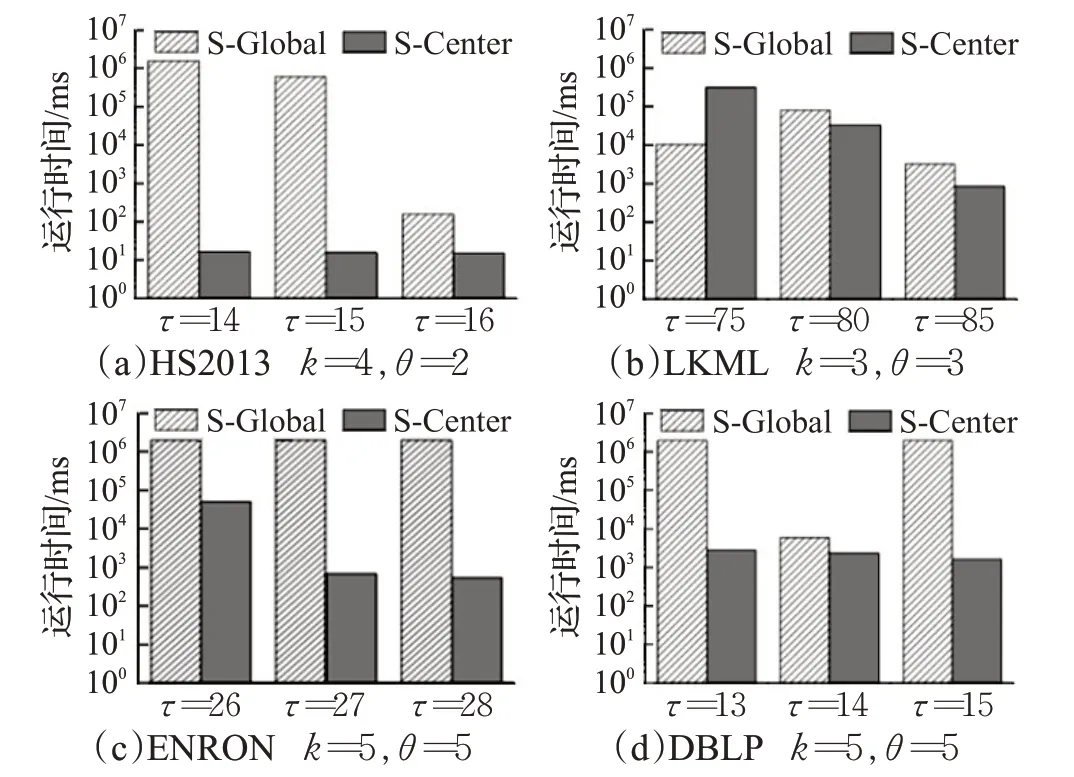
4.3 时间约束对算法性能的影响

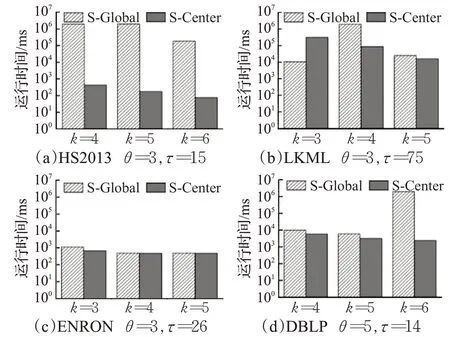
4.4 结构约束对算法性能的影响
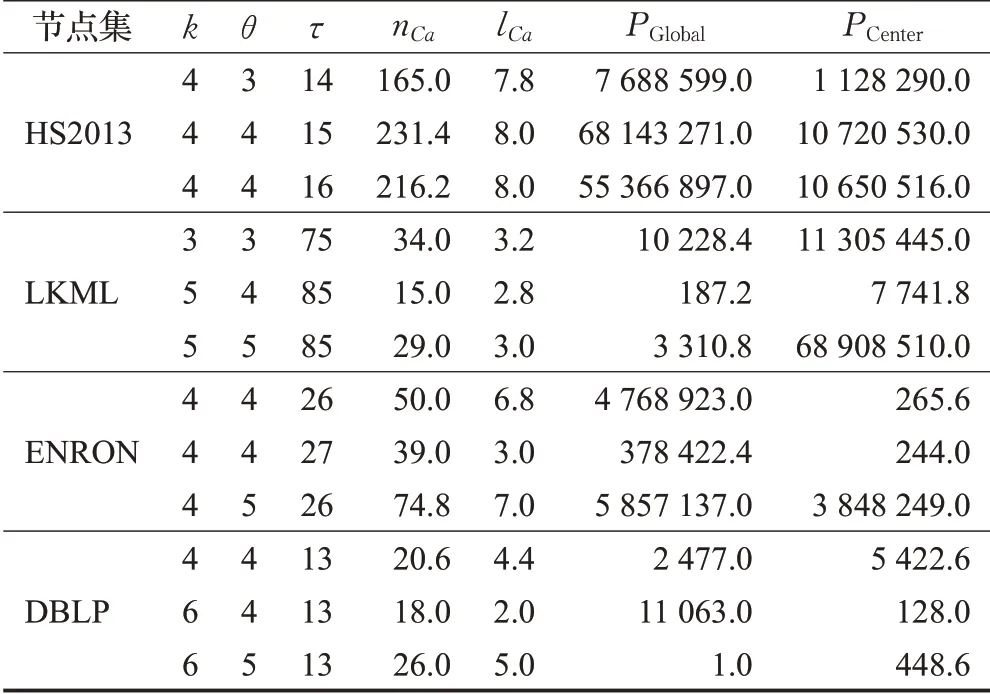
4.5 枚举削减规则对运行效率的影响
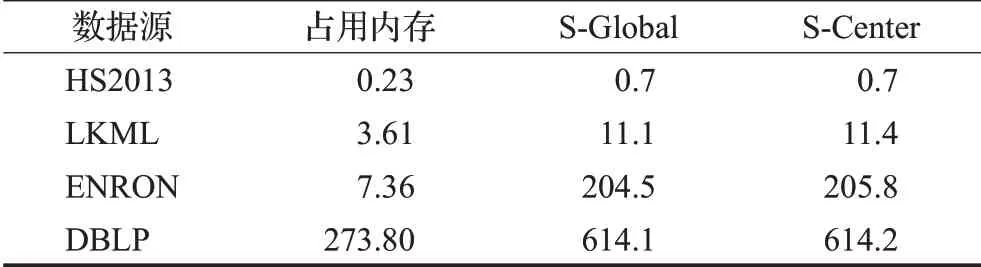
4.6 算法的内存开销
4.7 时间约束对结果质量的影响
5 结语

