一种深度回声状态网络的输入尺度自适应算法
刘 鹏,叶 润,闫 斌,谢 茜,刘 睿
(1.电子科技大学 自动化工程学院,成都 611731;2.国网四川省电力公司电力科学研究院,成都 610041)
0 概述
深度神经网络在图像处理[1]、语音识别[2-3]、数据建模[4]等领域得到广泛应用并取得重要研究成果,显示出层级神经网络结构在特征学习与迁移中的性能优势。在自然语言处理(Natural Language Processing,NLP)、基于视觉的同时定位与地图构建(Vision-based Simultaneous Localization And Mapping,VSLAM)[5]等实际工程应用中,研究的系统一般为与时间相关的动态系统。对于动态系统,典型特征是系统的状态随时间动态变化,输入与输出之间是一个暂态过程。递归神经网络(Recurrent Neural Networks,RNN)[6]由于神经元在时域上递归连接,使其具有丰富的时域行为,因此在动态系统理论研究和实际应用中受到广泛关注。深度卷积神经网络(Deep Convolutional Neural Networks,DCNN)[7]的网络层从低层到高层,所提取的特征由简单到复杂,正是因为这种层级结构,使得网络更容易训练,学习到的特征更容易泛化与迁移。DCNN 主要使用前向连接,如果将其运用到动态系统学习中,可以使用一个滑动窗口输入一个时间段内的信息。一般需要学习的动态系统延时特性是未知的[4],也就难以确定最优滑动窗口的长度,而且不同动态系统的延时特性不同,可能会使神经网络产生振荡、性能下降,甚至失去稳定性[8]。
研究人员通常利用RNN 提高动态系统的学习精度,其中长短期记忆(Long Short Term Memory,LSTM)网 络[9]是应用最 为广泛的RNN之一,由HOCHREITER 等在1997 年提出,目前已经集成在TensorFlow 等AI 开发平台中。LSTM 通常采用梯度下降方法进行学习[10],在一次权值调整过程中需要使用过去时刻的部分或全部数据,学习难度相对于前向网络成倍增加。JAEGER[11]在2005 年提出一种新型RNN,因输入信号在神经元之间来回衰减振荡类似于回声而被称为回声状态网络(Echo State Networks,ESN)。ESN 只需训练输出矩阵,训练过程等价于线性规划问题,相对于LSTM 而言训练难度显著降低,因训练简单,已在时间序列预测[12]、混沌系统学习[13-14]等任务中取得成功应用。SCHRAUWEN 等[15]利用ESN 的内部可塑性(Intrinsic Plasticity,IP)使得在特定输入下每一个神经元的输出都服从指数分布。IP 方法能在很大程度上提升ESN 的表达能力,但要对每一个神经元的输入进行调整,大幅增加了学习过程的计算代价。ESN 应用过程中需要选择内部状态矩阵的谱半径、输入尺度缩放系数等参数。为了最大限度发挥ESN的学习能 力,BIANCHI 等[16]提出均值 递归分析 方法,使用图形定性分析和定量分析判据,将ESN 推向临界稳定状态。
GALLICCHIO 等[17-18]提出一种基于ESN 的深度回声状态网络(Deep ESN,DESN)。文献[17]通过严格的实验分析多种输入方式对DESN 不同层之间的延时特性的影响。实验结果表明,堆栈形式的DESN 表现出更好的多尺度时域特性,而且合理选用不同谱半径的内部状态矩阵和弱积分参数能增强这种特性。文献[18]对如何选用DESN 层数进行了深入研究,提出一种基于频谱分析的层数选用方法。虽然文献[19-20]已将DESN 应用到一些实际工程中,但目前关于DESN 网络结构特性的研究尚少。文献[17-18]因为侧重点是在分析时域特性而不是预测精度,所以并未与传统ESN 进行预测精度对比,而在实际工程应用中,所需学习模型的时域特性本身是未知的,不能有效表明DESN 对不同延时系统预测精度的影响。为更好地利用DESN 的多尺度时域特性,本文将DESN 内部状态和输出矩阵进行可视化分析提出一种输入尺度自适应算法,通过学习两种数学模型完全已知的动态系统,分析改进后DESN 的性能优势,并与ESN 进行预测精度对比。
1 DESN 结构与训练算法
DESN 的基本单元是浅层ESN。本节首先介绍浅层ESN 结构和数学形式,然后介绍DESN 结构和基于广义逆的训练算法。
1.1 浅层回声状态网络
浅层ESN 的基本结构如图1 所示,其中,u表示输入向量,Wi表示输入权重,W表示内部状态矩阵,Wo1表示内部状态到输出的权重,Wo2表示输入直连到输出的权重,Wb表示输出反馈矩阵。ESN 对参数选择的唯一限制就是需要满足回声状态特性[11],等价于状态遗忘或输入遗忘特性,也就是说内部状态的初值以及某个时刻的输入在经历足够长的时间后,对系统输出产生的影响可以忽略不计。
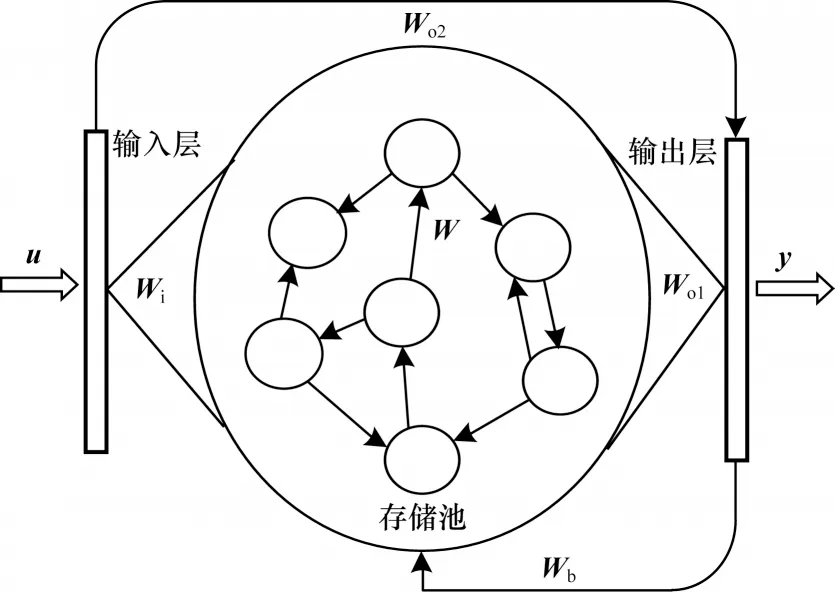
图1 浅层ESN 基本结构Fig.1 Basic structure of shallow ESN
输出反馈的引入能加快ESN 初始化过程,使内部状态初值的影响快速消失,但由于输出反馈会使回声状态特性受输出矩阵的影响,ESN 的鲁棒性会降低。一般在进行理论分析时,不考虑输出反馈的引入,而在实际工程应用中则可以通过引入输出反馈优化学习精度。
ESN 的数学表达形式可以分为内部状态x和输出向量y两部分,如式(1)所示:
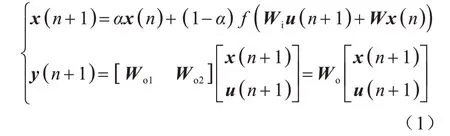
其中:弱积分参数α表示当前状态与上一时刻状态的关联程度,满足0≤α<1,通常而言参数α取决于所需学习的动态系统和采样时间间隔;激活函数f选取tanh 双曲正切函数,单个神经元的输出范围为-1~1。设ρ和σ分别表示W的谱半径和奇异值。若σ<1,则回波状态特性一定能得到保证,若ρ<1,则回波状态特性在大多数情况下能得到保证。
1.2 深度回声状态网络
如图2 所示,DESN 结构是一种堆栈形式,外部输入只作用于第一层神经元,其他每一层都以前一层输出为输入。如果将外部输入引入到每一层,则DESN 的多尺度时域特性会被削弱。
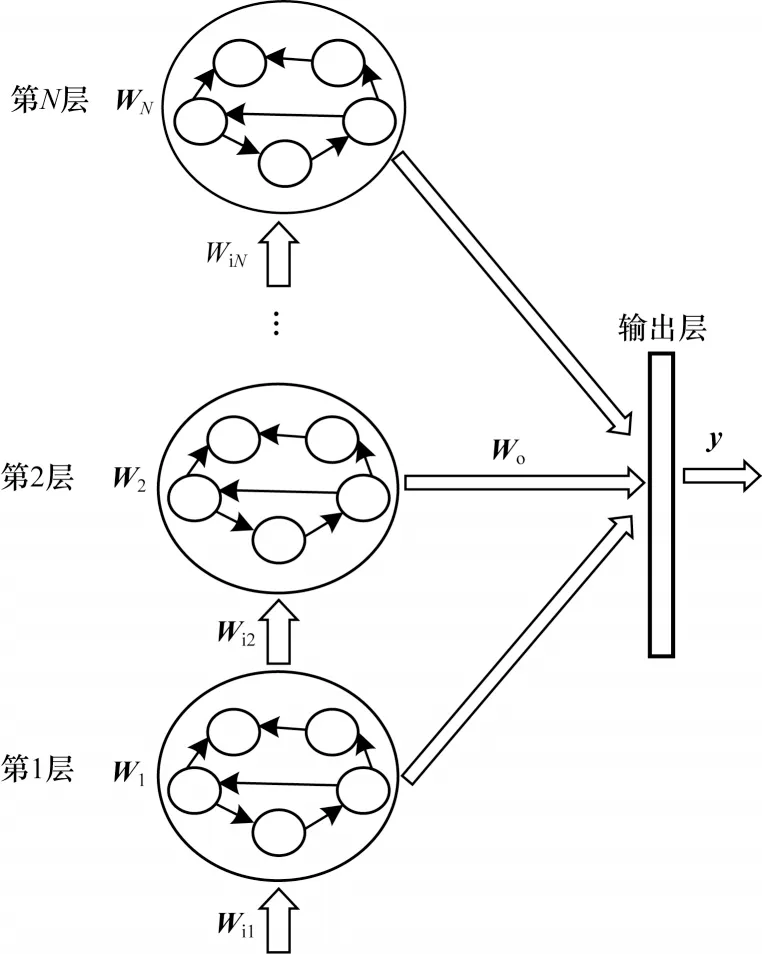
图2 DESN 结构Fig.2 Structure of DESN
每一层的状态如式(2)所示,形式上与式(1)保持一致。在DSEN 中,不同层之间可以选择不同的弱积分参数和不同的谱半径。

其中:k=1,2,…,N;u1表示外部输入,u2~uN表示前一层的输出。
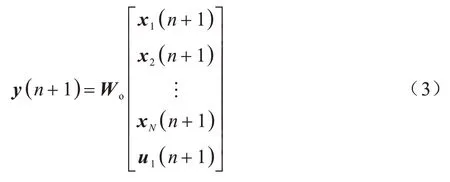
DESN 和ESN 只需训练输出矩阵Wo。输入矩阵Wi选为元素值在-1~1 的随机矩阵,W的选取需保证满足回声状态特性,参数α可以在不同层之间选择不同的值。
算法1基于广义逆算法的输出矩阵训练
步骤1初始化各层输入矩阵Wik为-1~1 的随机矩阵,随机生成各层状态矩阵Wk,计算Wk的奇异值σk,将Wk除以奇异值σk。
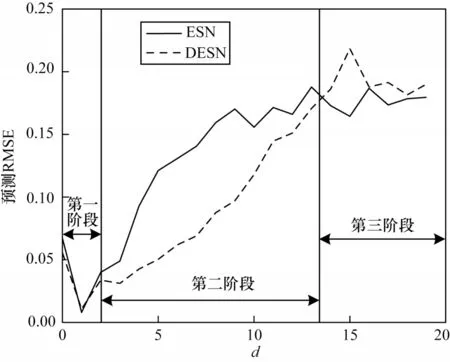
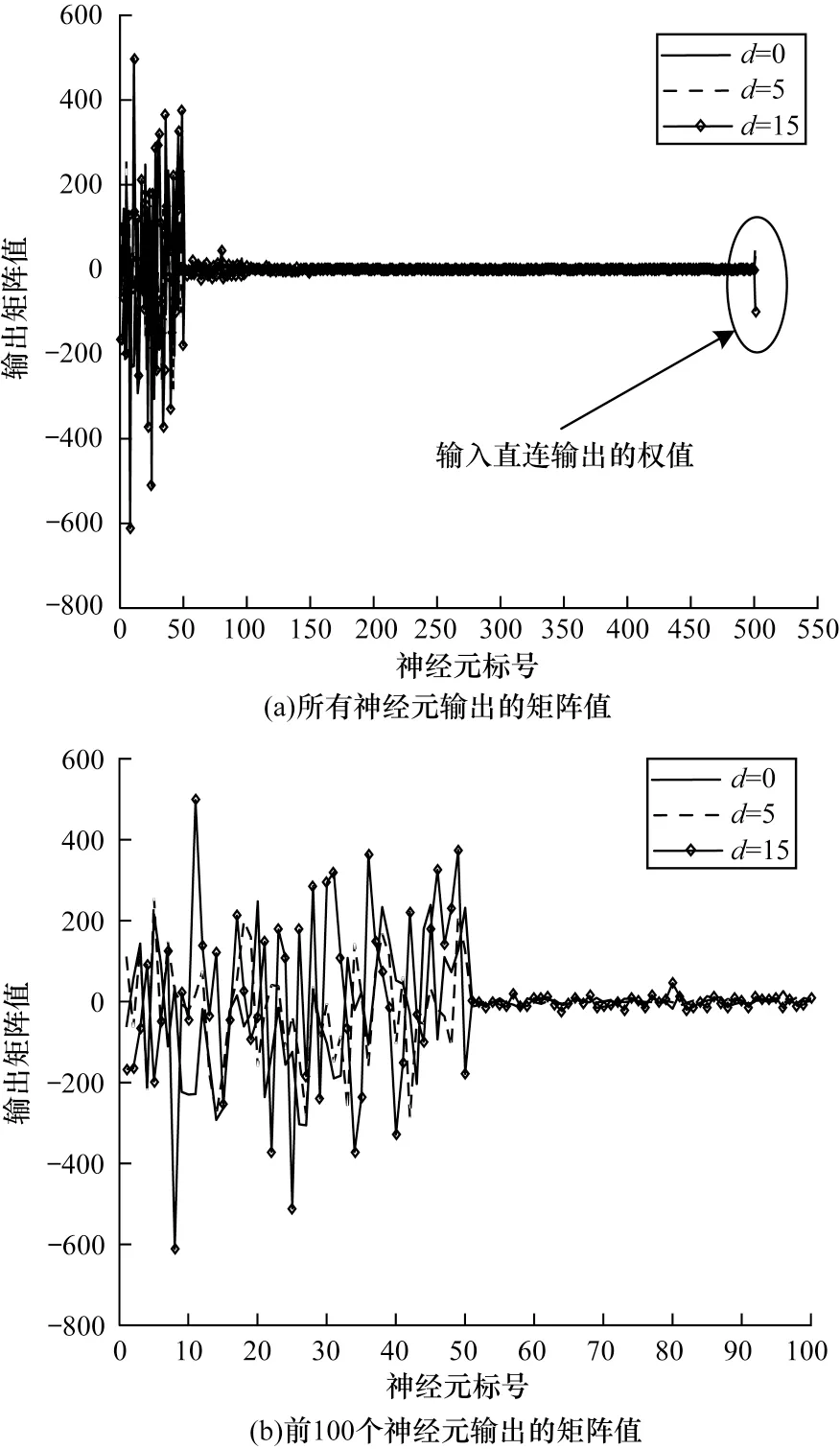
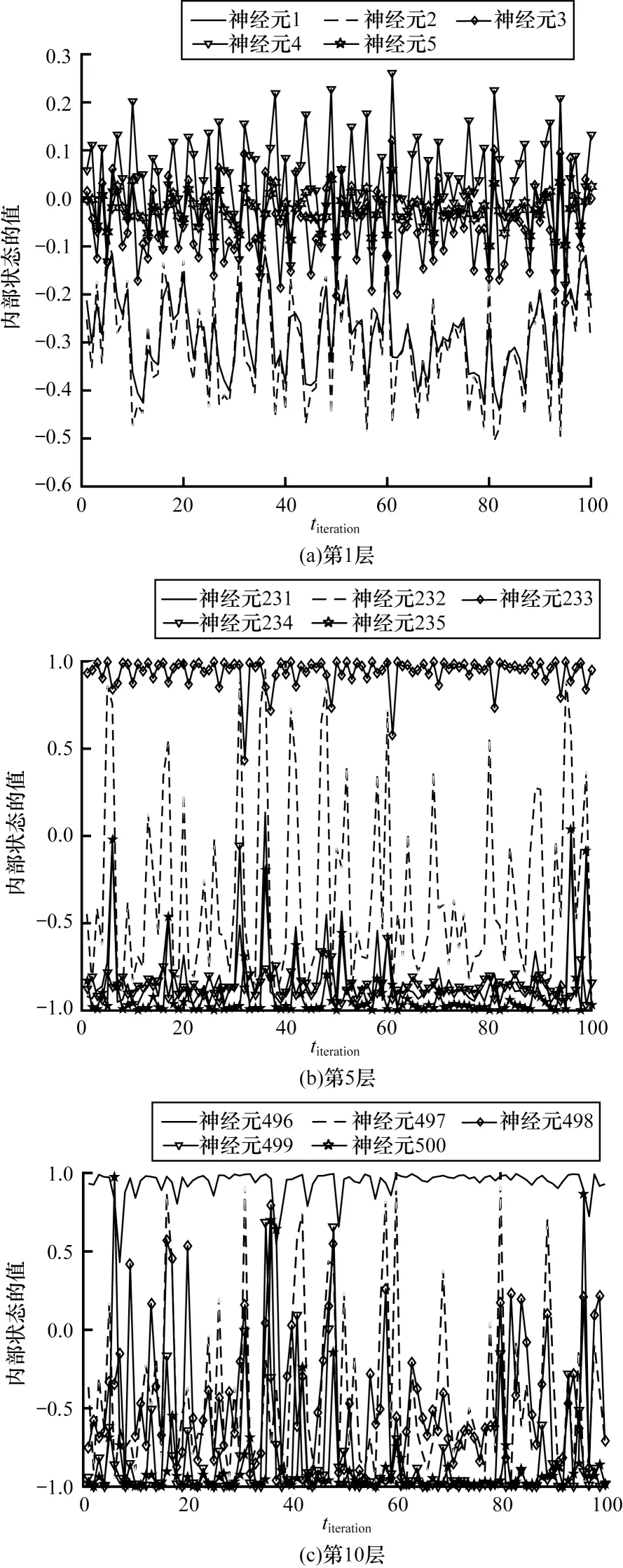
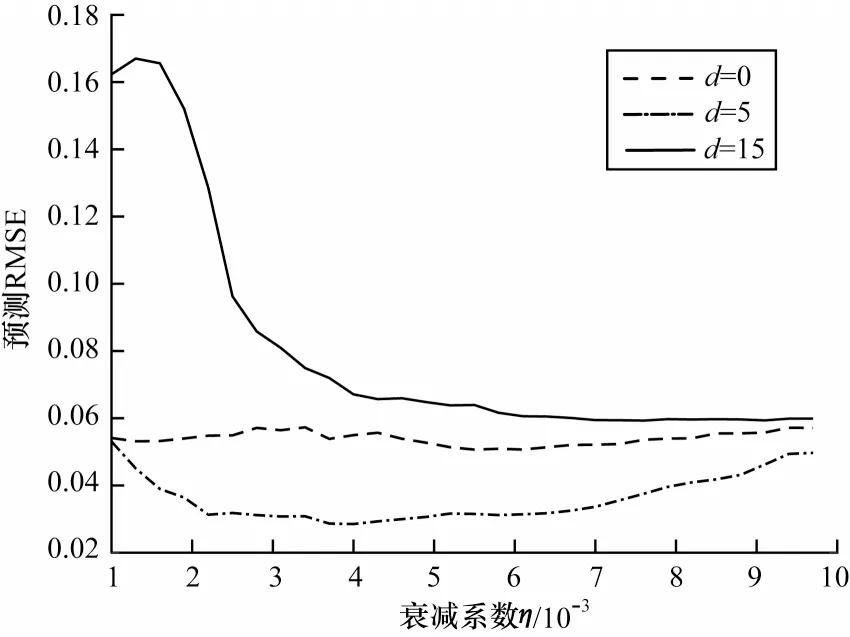
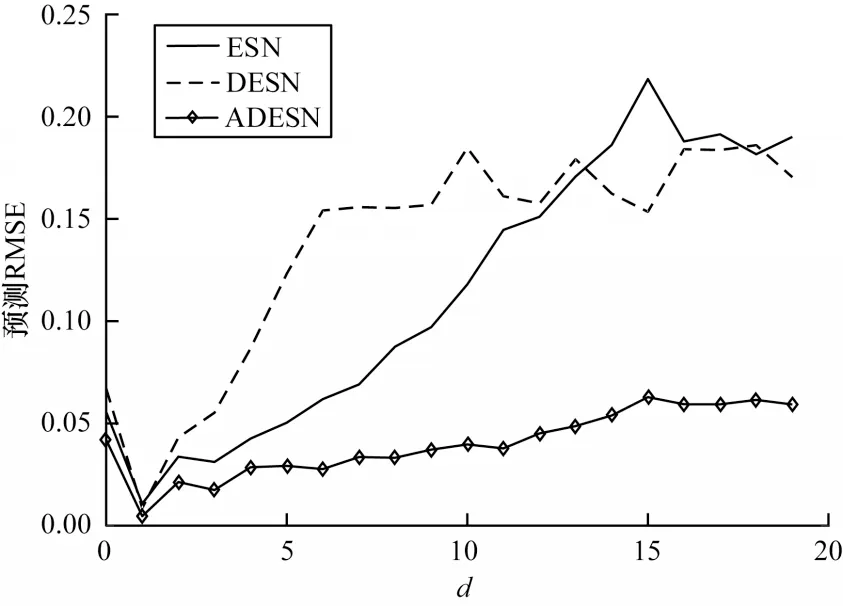
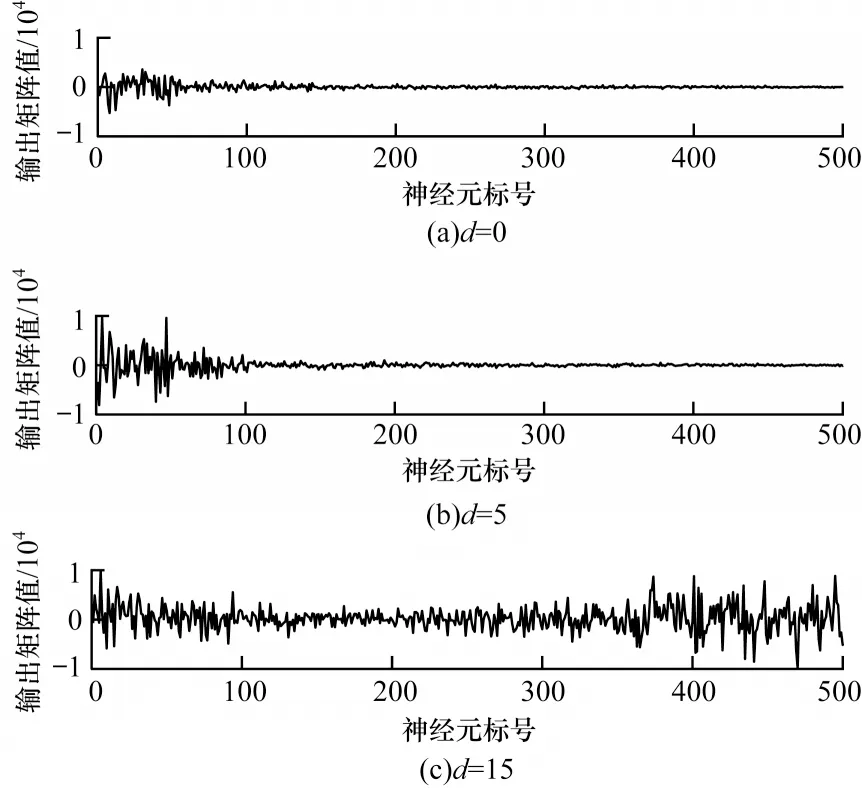
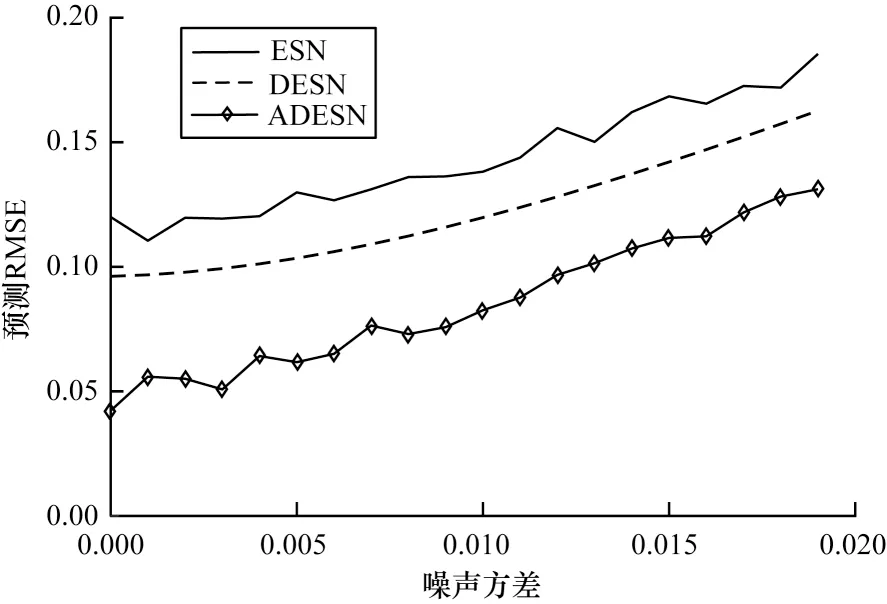
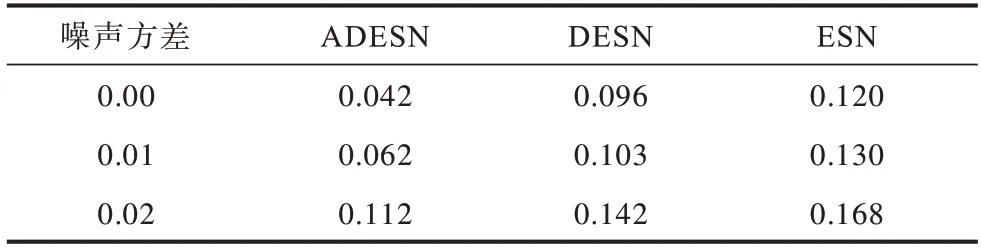
步骤2选取训练集(u(t),Yd(t)),其中0 步骤3使用广义逆算法计算输出矩阵,如式(5)所示: 为研究DESN 多尺度时域特性,选用具有不同延时特性的动态系统作为被学习对象。通过对比DESN 与普通ESN 的预测均方根误差(Root Mean Square Error,RMSE),分析DESN 多尺度时域特性在预测精度上的优势和限制因素。 参考滑动平均模型NARX[21],并添加延时项使动态系统有更加丰富的时域特性,如式(6)所示: 其中:d表示延时,d=0,1,…,19;输入u为0~1 的均匀分布。 ESN 选取弱积分参数为0.7、神经元个数为500,DESN 选取弱积 分参数为0.0,0.1,…,0.9,共 有10 层,每层的神经元个数为50。ESN 和DESN 的激活函数均为tanh,训练算法使用广义逆算法。训练样本和测试样本均取自式(6)所示的动态系统,第1 次实验延时设置为0,第2 次实验延时设置为1,依此类推直至延时为19。在每次数值分析过程中,训练集和测试集都采样1 000 组数据。同时,为了避免初始状态设置对动态系统的影响,前50 步迭代的数据被丢弃。 图3 给出了DESN 与ESN 的预测RMSE 随延迟时间的变化曲线,大致可分为三阶段:第一阶段,延时弱影响阶段,DESN 和ESN 预测RMSE 相近;第二阶段,延时较影响阶段,DESN 预测RMSE 明显小于ESN;第三阶段,延时强影响阶段,DESN 预测RMSE大于ESN 预测RMSE。在第一阶段中,由于延时特性不明显,因此DESN 和ESN 预测性能相近,此时DESN 多尺度时域特性的优势并未显现。在第二阶段 中,当d=5 时,DESN 相对于ESN预测RMSE降低超过50%。由于DESN 更高层的网络记忆输入的时间更长[17-18],如果在第二阶段中连接高层网络的输出矩阵绝对值相对增大,那么就证明DESN 多尺度时域特性提升了其预测能力。在第三阶段中,DESN预测性能劣于ESN,只有进一步分析,才能解释该阶段的反常现象。 图3 DESN与ESN学习不同延时NARX模型的预测RMSE对比Fig.3 Comparison of forecast RMSE between DESN and ESN when learn NARX model with different delays 图4 给出了DESN 的d取0、5、15 时的输出矩阵Wo在各层中的分布情况。从图4(a)可以看出,输出矩阵绝对值大的元素全都分布在第1 层和输入直连输出中。图4(b)为图4(a)的局部放大图,从图4(b)中并未发现输出矩阵值会随着学习系统的延时增加而发生明显移动,由此得出图3 中第二阶段DESN 预测能力的提升不能归结为多尺度时域特性的影响。 图4 不同延时的DESN 输出矩阵对比Fig.4 Comparison of DESN output matrixes with different delays 图5 给出了d=15 时DESN 第1、5、10 层部分神经元的内部状态,其中横坐标titeration表示迭代时间。在第5 和10 层中可以看出,超过一半神经元处于饱和工作状态,即绝对值在大部分时间都维持在一个较高水平。这类神经元不仅自身动态性能差,而且会使得其他具有丰富动态的神经元、输出权值极小。实际上,从第3 层开始,在后续层中大量神经元处于这种饱和工作状态。从内部状态可视化分析可知,在DESN 高层网络中容易出现处于饱和工作状态的神经元,如果能够抑制这种饱和状态,则有可能更好地发挥DESN 多尺度时域特性的优势。 图5 DESN 内部状态Fig.5 Internal state of DESN 由于DESN 每一层的网络都满足回声状态特性,也就是说只要时间足够长,输入信号会被逐渐遗忘。然而,当输入信号足够强时,遗忘的速度小于输入的速度,使得部分神经元处于饱和工作状态。为了保持DESN 多尺度时域特性,需要避免神经元处于饱和工作状态。 判断神经元是否处于饱和工作状态主要包括状态保持恒定及维持较高值两个条件。状态保持恒定意味着方差小。在方差小的情况下维持高值意味着绝对均值相对较大。通过设定合适的方差与均值的阈值,综合判断神经元是否处于饱和状态。如果处于饱和状态,则意味着输入速度要大于遗忘速度,需减弱输入。同一层的神经元通过内部状态矩阵W彼此互联,对一个神经元的输入会立即影响其他神经元。因此,对于具有饱和工作状态的神经元的层,应该整体减小输入才能有效抑制饱和工作状态。另外,每一层处于饱和工作状态的神经元个数不同,处于饱和状态的神经元越多,输入的衰减程度就越大。 算法2饱和状态抑制 步骤1对于内部状态序列x(t),0 步骤2判断当前时刻是否需要进行一次权值调整,判断依据是与上一次权值调整的时间间隔是否达到阈值ΔT。若需要调整,则进入步骤3,否则返回步骤1 继续递推估计均值和方差。 步骤3逐层分析各个神经元的均值和方差,若|m|>mmin且D 步骤4分层统计处于饱和状态的神经元个数n,第k层输入权重按式(9)动态调整: 在算法2 中,衰减系数η是关键参数,若值过大会使内部状态工作在零值附近,若值太小会达不到调整输入权重的效果。使用算法2 改进的DESN 称为输入尺度自适应深度回声状态网络(Adaptive DESN,ADESN)。 算法3ADESN 训练 步骤1选定一个衰减系数η,在训练集上执行算法2,调整输入矩阵Wik,k=1,2,…,N。 步骤2在训练集上训练执行算法1,得到输出矩阵。 步骤3在验证集上测试DESN 预测性能,计算预测RMSE。 步骤4重复进行步骤1~步骤3,选取验证集上预测RMSE 最小的衰减系数η作为最终参数。 通过学习NARX 模型和单输入单输出系统来验证ADESN 的预测精度提升情况,并使用一个多输入多输出(Multiple Input Multiple Output,MIMO)系统[21]测试ADESN 的适用性。 数据集共分为训练集、验证集和测试集,每一个样本采样数量为1 000。DESN 和ESN 参数设置参考2.1 节。ADESN 衰减参数η、方差阈值Dmax和均值阈值mmin需设定,将在4.1 节中进行讨论。 Dmax和mmin的选择会对神经元是否处于饱和状态的判断产生影响。如果Dmax值选择过大,条件D 为了避免参数之间的耦合,设定Dmax=1×10-4、mmin=0.1,分析关键参数η对ADESN 的影响。选取ADESN 衰减系数η区间为0.001~0.01,衰减系数η对不同延时的NARX 模型预测RMSE 的影响如图6所示。从图6 可以看出:当延时d=0 时,RMSE 随η的变化略有波动;当延时d=5 时,RMSE 随η的增大先减小后增大;当延时d=15 时,RMSE 随η的增大逐渐减小并趋于稳定。由此可见,η对系统的影响与系统的时延特性有关,系统时延越大调整η产生的影响越大。因此,参数η需按算法3 中描述针对不同时延的动态系统进行优化处理。 图6 不同延时测试集上衰减系数η 对预测RMSE 的影响Fig.6 Effect of attenuation coefficient η to forecast RMSE on test set with different delays ESN、DESN 和ADESN 在不同延时的NARX 模型上的预测RMSE对比如图7所示,具体数据如表1所示。由图7 和表1 可以看出:ADESN 在全过程中都具有最佳预测精度,当d超过5时预测RMSE约为ESN的30%,极大地提升了高延时系统的预测精度。ADESN和ESN具有的神经元数目相同,但ADESN 对于高延时系统能显著提升预测精度,其原因为充分发挥了多层结构的多尺度时域特性的优势。 图7 不同延时的ESN、DESN、ADESN 预测RMSE 对比曲线Fig.7 Comparison curves of forecast RMSE among ESN,DESN and ADESN under different delays 表1 不同延时的ESN、DESN、ADESN预测RMSE对比数据Table 1 Comparison data of forecast RMSE among ESN,DESN and ADESN under different delays 从图8 可以看出,随着延时的增加,权值逐步向高层网络移动。高层网络记忆输入的时间更长,如果高层网络对应的权值更大,则意味着系统的延时特性更强。这种随着网络层次增加对输入的记忆时间增强的特性就是多层结构的多尺度时域特性。 图8 不同延时下ADESN 输出矩阵在各层神经元之间的分布Fig.8 Distribution of ADESN output matrixes among neurons in each layer under different delays 图9 给出了d=15 时ADESN 第1、5、10 层部分神经元的内部状态。相对于图5中DESN内部状态,ADESN在各层网络中不再有处于饱和工作状态的神经元,各层饱和状态神经元的消除一方面使得网络动态性更强,另一方面也使本来处于正常状态的神经元获得较大的输出权值。综上所述,ADESN 能够消除处于饱和状态的神经元,充分发挥多尺度时域特性的优势。 图9 ADESN 内部状态Fig.9 Internal state of ADESN 应用多输入多输出系统(如式(10)、式(11)所示)进一步测试ADESN 多尺度时域特性优势。 其中:u1和u2表示值 在0~1的均匀分布;v1和v2表示均值为0、方差为0.00~0.02 的高斯噪声。由于方差不同,因此以0.001 为间隔共测试20 种不同工况。 图10 给出了ESN、DESN 和ADESN 在不同噪声条件下对多输入多输出系统的预测RMSE,具体数据如表2 所示。由图10 和表2 可以看出,ADESN 依然具有最佳的预测能力,但是随着噪声的增加,3 种网络都严重劣化,在后期研究工作中需考虑提升网络对噪声的鲁棒性。 图10 不同噪声方差的ESN、DESN、ADESN 预测RMSE对比曲线Fig.10 Comparison curves of forecast RMSE among ESN,DESN and ADESN under different noise variances 表2 不同噪声方差的ESN、DESN、ADESN 预测RMSE对比数据Table 2 Comparison data of forecast RMSE among ESN,DESN and ADESN under different noise variances 针对传统DESN 内部状态容易陷入饱和工作状态,不能重复利用多尺度时域特性的问题,本文通过自适应地调整输入矩阵构建一种深度回声状态网络ADESN,使用网络内部状态的均值和方差判断神经元是否处于饱和状态,加强网络动态预测能力。对两个不同动态系统的学习结果表明,ADESN 相对DESN 和ESN 预测精度成倍提升。在后续研究中将改进ADESN 的抗噪能力,进一步提升其在实际噪声环境中的预测精度。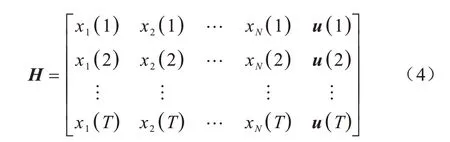

2 DESN 可视化分析
2.1 数值计算模型设定
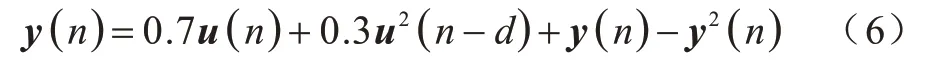
2.2 可视化分析
3 DESN 输入尺度自适应算法
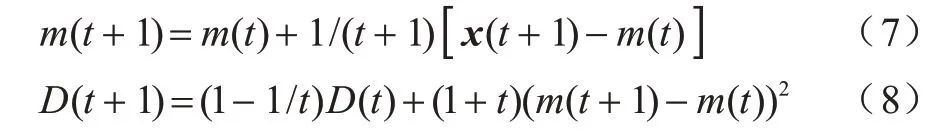
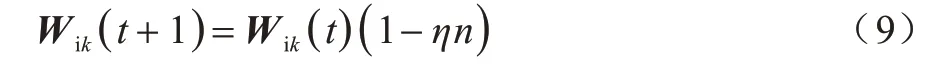
4 数值计算结果与分析
4.1 ADESN 参数选择
4.2 NARX 模型预测


4.3 多输入多输出系统预测
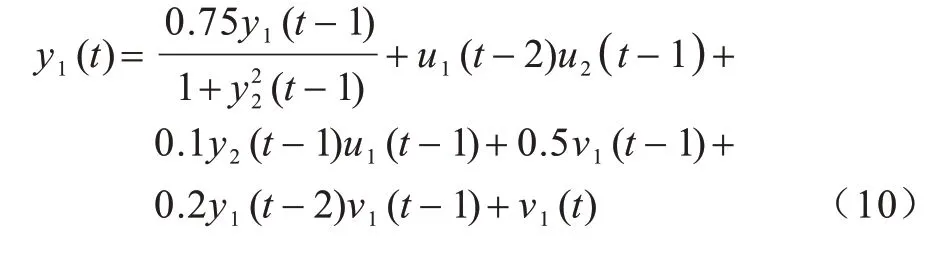
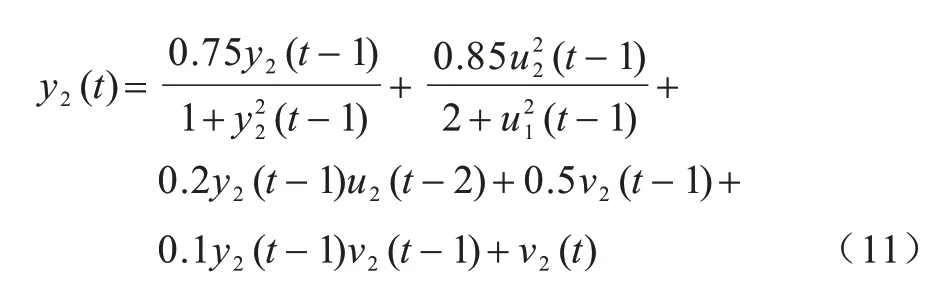
5 结束语

