连续时间区间内的频繁词序列挖掘算法

王 璐，刘晓清，何震瀛

（1.复旦大学 软件学院，上海 200441；2.复旦大学 计算机科学技术学院，上海 200433）

0 概述

互联网和人工智能等信息技术的快速发展，使得新闻报道、博客推文、用户评论等大量文本数据呈指数级增长，这些文本数据中蕴含着时事政治、热点话题等具有重要价值和研究意义的信息。但由于网络中文本数据海量、繁杂等特点，人们难以在大量篇幅文本中直接获取有效信息，因此快速高效地在海量文本数据中提取有效信息成为研究人员关注的重点。以词序列形式挖掘文本中频繁出现的短语成为用户获取关键信息及进行文本集探索的有效方式之一。频繁词序列挖掘是将频繁出现的词序列看作能够反映文档主题内容的短语，挖掘在文本集合中频繁出现的词序列。频繁词序列挖掘工作在短语挖掘［1］、文本聚类［2］、话题检测［3］等任务中发挥重要作用。EL-KISHKY 等［4］在语料库中抽取频繁词序列作为短语候选集，用于短语挖掘。BEIL 等［5］挖掘文本集合中的频繁项集，使用频繁项集作为候选簇进行文本聚类。MA［6］检测滑动时间窗口中的词频统计等信息，并将其应用于新闻流的热点话题提取模型。在这些工作中，频繁词序列挖掘是目标任务中重要且耗时的步骤，因此高效的挖掘方法能够带来整体任务效率的提升。

在很多实际应用中，新闻、博客等文本数据通常会以时间为单位进行组织并存储。近年来，文献［7-9］等诸多研究工作都聚焦在流数据、时空数据等具有时间属性的文本数据中进行文本挖掘。因此，研究时间维度下的文本挖掘工作同样具有重要意义。在一段时间区间内持续频繁出现的短语，更能体现热点话题和文章内容趋势。例如，当使用《纽约时报》新闻作为输入数据时，划定时间区间为“2020 年3 月”、频次阈值为20，在这段连续时间区间内进行频繁词序列挖掘，发现获得的频繁词序列为“冠状病毒实时更新”、“冠状病毒的简报”和“伯尼·桑德斯”等，通过这些频繁词序列，可以看出该阶段的热点话题更多与新冠肺炎和美国大选的候选人选问题相关。然而，在面对海量文本数据并无法完全掌握文本内容的情况下，用户难以在一次查询中准确设置阈值和时间区间，需要多次迭代查询从而完成挖掘任务。用户趋向于以探索性方式逐步进行挖掘，例如通过调整最小频次阈值的大小获取合适的关键短语集合，或通过调整时间区间来探索不同时间段内的热点话题的变化。传统频繁项集挖掘方法在修改最小频次阈值或数据集后需要重新进行挖掘，因此在海量文本数据库上进行频繁词序列挖掘时存在耗时严重的问题，无法达到频繁迭代的查询效率要求。

针对文本挖掘中热点话题检测、关键短语挖掘等实际应用场景，本文提出连续时间区间内的频繁词序列挖掘算法。使用频率树（Frequency Tree，F-Tree）作为基本索引结构支持高效的频繁词序列挖掘，同时设计频率树的序列化构建方式和多棵频率树的连续剪枝挖掘算法，快速寻找在连续时间区间内的热点短语信息。

1 相关工作

1.1 热点话题检测

热点话题检测主要关注在一段时间内持续受到关注和讨论的主题内容，近年来研究人员对于热点话题检测进行大量研究。文献［10］提出PCTF 方法，并将其用于查询一组词汇成为热词的最长持续时间。文献［11-12］在带有时空信息的数据流中，查找一段时间内发布的k个最相关的词汇或文档。文献［13］通过优化TF-IPDF 的计算过程，加快热点词汇查询效率。在上述工作中，热点话题的挖掘结果均以单个词汇为单位呈现。短语相比词汇在语意中更加完整，能够表达更准确的主题含义，在实际应用场景中，人们更倾向于使用短语作为主题表达方式。

1.2 频繁项集挖掘

频繁词序列挖掘问题类似于数据挖掘中的频繁项集挖掘问题［14］。在频繁项集挖掘中，以Apriori 算法［15-16］为代表的层次优先搜索方法通过遍历迭代数据集发现项集，以FP-Growth 算法［17］为代表的一系列算法根据数据信息构建FP-Tree，在此基础上进行频繁项集发现。Apriori 算法能够通过简单修改应用于频繁词序列挖掘问题，但由于算法需要多次扫描整个事务数据库，在大规模文本挖掘中效率低下。凭借良好的扩展性和易编写的特点，仍有一些研究人员［18-19］使用Apriori 类算法进行词序列挖掘。FP-Growth 类算法利用树形结构对原始数据进行索引，在挖掘过程中无需生成候选频繁项集，提高了算法效率。但在FP-Tree 的构建过程中，需要按照项集频繁度进行重新排序，打乱了项集之前的前后顺序和关联关系，对于频繁词序列挖掘任务而言，单词构成的词序列是有序且连续的。因此，上述频繁项集工作对于解决频繁词序列挖掘问题具有一定指导意义，但无法完全适用于频繁词序列的挖掘。

1.3 后缀树

与FP-Tree 类似，后缀树是一种多叉树型的数据结构，能够索引一个字符串的所有后缀。对于由给定字符串S 构成的后缀树T，T 中每个内部节点到叶子节点的路径均能够构成S 的一个后缀。如图1 所示，由字符串S=“I Know You Know I Know”构成的后缀树T 可以看出，S 包含两个以I 为起始点的后缀“I Know You Know I Know”和“I Know”。

图1 后缀树Fig.1 Suffix tree

后缀树的概念由WEINER［20］在1973 年提出，为了降低后缀树的存储代价，MCCREIGHT 等［21］对后缀树采取压缩冗余节点的方法，如图2 所示，每条边不再仅限于包含一个单词而是一个部分叉的字符串，使用$表示字符串结束。每个内部节点都至少具有两个子节点。为提高后缀树的构造效率，UKKONEN［22］在1995 年提出在 线构造字 符串后缀树的算法，能够从左向右对字符串进行处理，当遇到不同后缀时对后缀树的边进行分割，该方法具有线性的时间复杂度。

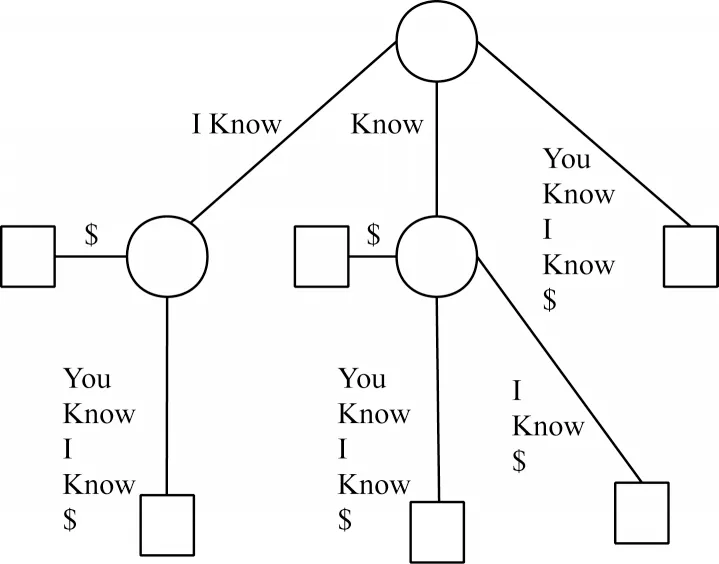
图2 压缩后缀树Fig.2 Compressed suffix tree

2 问题定义

本文研究的主要问题为根据用户给定的查询范围和最小频次阈值，快速找到查询范围内在所有最小时间区间上均满足频次阈值的词序列集合，实现对连续热点话题的检测。

定义1（时间区间T(x，y)）T(x，y)={tx，tx+1，…，ty}，1≤x≤y≤n表示时间区间，其中，t为最小区间间隔单位，ti为数据集的第i个区间间隔。T(1，n)表示包含整个数据集的完整区间，其中n表示包含的全部最小区间的个数。

定义2（带有时间属性的文本数据库D）数据集中的文本根据时间属性值分布在对应区间中，存储分布于时间区间T(1，n)内的文本数据库D={Di|1≤i≤n}，其中Di为时间属性值属于时间区间ti的文本数据。

定义3（词序列s（x，y））根据由有限个单词a组成的词典Σ，文本可表示为d={a1，a2，…，an}。词序列s(x，y)={ax，ax+1，…，ay}，s(x，y)∈D是由文本集合D中依次出现的单词组成的连续序列。

定义4（词序列的频次Freq(s，D)）对于给定的文本数据库D={D1，D2，…，Dn}，词序列s在D中的频繁度可表示为Freq(s，D)=|{d∈D：s⊆d}|，即词序列s在D中完整出现的次数。

定义5（连续时间区间内的频繁词序列查询query(D，θ，T)）对于分布在时间区间T(1，n)内的文本数据集D={D1，D2，…，Dn}，给定时间 区间子集T(x，y)和最小查询阈值θ，查询在所有最小时间子区间tx…ty上的所有 文本子集Dx…Dy均满足Freq(s，Di)≥θ，且不存在s的子串s'满足Freq(s'，Di)≥θ的所有词序列s构成的集合S。

3 算法描述

3.1 频率树

原始后缀树在边上记录子串起始位置等信息，同时后缀树通常作为单个字符串而不是文本集合的索引结构，无法很好地表示多条文本数据信息。本文对后缀树结构进行改进，提出频率树，使其可用于词序列频次的计算，实现词序列挖掘算法。F-Tree对于原始后缀树结构修改如下：

1）给定一个包含n条文本数据的文本集合D={s1，s2，…，sn}，F-Tree 是一个包含n条文本数据的所有后缀的后缀树。在构造F-Tree 时，在插入第i条文本数据s={a1，a2，…，an}时，在s后填充唯一的终止标记符$i，得到s={a1，a2，…，an，$i}。

例1频率树与仅索引单条字符串的后缀树不同，能够包含多条文本串的所有后缀。使用不同终止符保证了文本数据的所有后缀为唯一存在，每个后缀均由唯一的叶节点表示，避免了后缀数据被隐藏在内部节点中或频次计算被忽略的问题。例如，根据UKKONEN算法在图2 的后缀树中插入新的句子“I Know”时，原始后缀树在读取到与边“I Know”完全匹配后，判断完成本次插入而无须进行任何操作，导致对于完全相同的后缀错误的频次计算。如图3 所示，对于由“I Know You Know I Know”和“I Know”构成的F-Tree，当修改为插入“I Know $2”时，能够与“I Know You Know I Know$1”中“I Know”后缀在终止符位置进行区分，从而保证频率统计的正确性。

图3 频率树Fig.3 Frequency tree

2）F-Tree 的每个节点由节点标号i与频次属性值freq 组成node(i：freq)，用freq 来表示由根节点0到当前节点i的路径拼接得到的词序列s[0，1，…，i]的频次，即对于由数据集D构成的具有n个节点的F-Tree，树中的任意节点i∈(1，n)，freqi=Freq(s[0，1，…，i]，D)。

例2以图3 中节点2 为例，节点9 存储的freq=1，即由根节点0 到节点9 的路径与路径拼接成的词序列“Know I Know $1”在数据集中的出现频次为1。同理，节点1 的freq=3 表示“I Know”词序列出现频次为3。

引理1在F-Tree 中，叶子节点的freq 为1。

证明如图3 所示，F-Tree 中由根节点到叶子节点的路径表示文本数据后缀，由于每条插入数据采用不同终止符进行标记，因此数据集中所有后缀均是唯一的，即叶子节点的freq 为1。

引理2每个内部节点的freq 等于其直接连接子节点的freq 之和。

证明数据集中词序列s出现频次Freq(s，D)等于数据集中以s为前缀的所有后缀个数，由于每个后缀能够由叶节点唯一表示，根据引理1，对于根节点到i的路径构成的词序列s[root，i]，Freq(s，D)等于i的所有孩子节点中叶节点freq 之和，即等于与节点i直接连接的孩子节点的freq 之和。

引理3如果由根节点到节点i的路径组成的词序列s[0，i]的频次为n，那么对于i的所有孩子节点，根节点到孩子节点的路径组成的词序列频次一定小于等于n，即∀j∈child(i)，Freq(s[0，j]，D)＜Freq(s[0，i]，D)。

证明由于每个节点的freq 等于其直接孩子节点的freq 之和，如果该节点的频次小于设定阈值，那么它的孩子节点freq 一定小于设定阈值，即如果一个词序列s的出现频次为n，那么所有以s为前缀的更长词序列出现频次一定小于等于n。

3.2 基于频率树的频繁词序列挖掘算法

由F-Tree 节点的freq 特点可知，通过对比节点freq 值与频次阈值的大小，可以判断词序列是否符合查询要求。当使用F-Tree 进行最小频次为θ的频繁词序列挖掘时，可以通过对F-Tree 进行深度遍历实现。根据引理3，F-Tree 能够通过节点freq 值与阈值θ的对比对F-Tree 进行剪枝，从而减少遍历范围，提高查询效率。遍历F-Tree 到达某个节点时，如果它的freq 大于最小阈值，记录边中的词序列并继续向下遍历；直到节点freq 不再满足阈值要求，那么对应后缀不再满足频繁词序列要求，向上回溯到父节点；如果节点满足阈值且它的所有孩子节点均不满足阈值要求，那么由根节点到该节点的记录的路径边词序列即为满足要求的一个最长频繁词序列。基于频率树的频繁词序列挖掘算法（TS_Mining）描述如算法1 所示。

算法1基于频率树的频繁词序列挖掘算法

使用F-Tree 的频繁词序列挖掘算法能够获得每个单位时间区间内的频繁词序列结果。为了进行连续时间区间范围内的频繁词序列挖掘，需要对每个单位时间区间内的挖掘结果进行合并，得到在所有单位时间区间内均满足查询条件的词序列。在对单个F-Tree 挖掘结果进行合并时，一个基础的取交集方法是对所有的结果集合逐个合并取交集，从而获取满足要求的最终结果集合。对第i个时间区间的词序列集合Si中的词序列s逐个进行遍历，获取s与前i-1 个区间合并的结果集合S′i-1的最长交集，将不为空的词序列加入S′i，从而得到前i个区间的词序列结果集合S′i。连续区间查询的取交集算法（Intersection）描述如算法2 所示。

算法2连续区间查询的取交集算法

3.3 改进的剪枝挖掘算法

算法1 与算法2 在对每个F-Tree 都进行阈值为θ的挖掘的同时，需要对每个单位时间区间内的结果集合进行重复取交集操作，从而找到在所有F-Tree中均满足查询条件的词序列。从结果来看，此类算法需要扫描经过更多的路径并进行额外的取交集计算，造成了效率损失。因此，本文在此基础上进行改进，充分利用F-Tree 的数据结构，在F-Tree 扫描过程中完成取交集操作，将频率树的频繁词序列挖掘算法改进为剪枝挖掘算法（TS_Pruning），具体描述如算法3 所示。

算法3改进的剪枝挖掘算法

使用前i-1 个单位时间区间内的结果作为输入，对第i棵F-Tree 进行扫描剪枝，获得在前i个单位区间内均满足查询条件的结果集合。在剪枝查询算法中，对于输入集合的每个词序列s，在区间i中的F-Tree 中以根节点为起点，自上而下在F-Tree 中查找词序列s所经节点是否满足查询阈值，从而找到满足查询条件的最长前缀。该算法充分利用了第i-1 个区间的挖掘结果，能够减少F-Tree 需要扫描的范围，同时无须对结果集合进行合并，减少了多次遍历的时间代价。后缀树的词序列匹配算法（find_prefix）描述如算法4 所示。

算法4基于频率树的词序列匹配算法

3.4 外存频率树加载

当使用大规模文本数据集进行查询时，常规主机的内存往往无法容纳全部频率树索引结构。根据F-Tree 结构可以看出，树中边信息与节点信息仅与文本数据集相关，而与每次查询的设定阈值无关。因此，当面临内存中无法容纳所有F-Tree 索引结构的情况下，通过序列化方法构建每个最小区间内的后缀树并存储在本地文件中，当进行查询时，只需通过反序列化将时间区间范围内的后缀树进行结构恢复，而无须对时间区间内的全部文档重新遍历来构建后缀树。当进行连续时间区间内挖掘时，不再需要多次根据不同时间区间内的文本集合构造F-Tree。相对于读取原数据并重新构建F-Tree 的方法，序列化方法能快速还原F-Tree 结构，从而提升整体挖掘效率。

3.5 时间复杂度分析

假设文本数据集中文本长度为m，查询时间区间长度为T，在单位时间区间下挖掘的频繁词序列的总长度平均为L1，最终频繁词序列结果集合总长度为L2。

F-Tree 构造具有与压缩后缀树相同的时间复杂度，根据文献［9］可知，F-Tree 构造的时间复杂度为O（m）。对于朴素F-Tree 的频繁词序列挖掘算法，需要对F-Tree 进行深度遍历找到满足查询要求的所有路径，查找长度为L1，对于所有区间下的F-Tree 挖掘的时间复杂度为O(T×L1)。同时，取交集的结果集合的合并方式共需要进行t次合并操作，每次合并操作对两个集合进行遍历，时间复杂度为因此，总的时间复杂度为改进的剪枝挖掘算法将第i-1 个区间挖掘结果集合作为新的时间区间挖掘的输入，避免结果合并带来的时间代价。同时，在F-Tree 的挖掘过程中，只需对上一个区间的结果集合路径进行遍历剪枝，利用剪枝算法避免无效路径的搜索，从而降低时间复杂度。在每次挖掘过程中，遍历路径长度L'满足L1＜L'＜L2，因此时间复杂度将趋近于O(T×L2)，进一步降低了挖掘时间复杂度。

4 实验结果与分析

4.1 实验设置

4.1.1 实验数据集

实验使用2 个开放数据集进行测试：twitter 数据集采用2009 年4月至2009年6月的16万条twitter 文本；blogs 数据集采用来自blogger.com 的2004 年1 月至2004 年12 月的博客文章［23］，该语料库共包 含681 288 篇文章。在实验中设置单位时间区间长度为1 周。为了更加符合现实应用场景，使用NLTK 自然语言处理库对文本集合进行预处理，包括按照标点和停用词对文章进行断句、词形还原等。表1 给出了数据集的详细信息。

表1 数据集详细信息Table 1 Dataset details

4.1.2 实验环境和对比算法

实验算法均由C++11 语言编写，gcc 编译，运行环境为2 GHz Intel Core i5 四核处理器，16 GB 内存，macOS Catalina 10.15.7 操作系统。

实验将Apriori 频繁项集挖掘算法作为对比算法，并分别修改频繁词序列查询的各项参数，以验证本文提出的基于频率树的频繁词序列挖掘算法TS_Mining 和改进的剪枝挖掘算法TS_Pruning 的有效性。

4.2 性能分析

对于twitter 数据集，设置查询的起始时间为2009 年4 月1 日，查询时间区间T为1、3、6、9、12 周；对于blogs 数据集，设置查询的起始时间为2004 年1 月1 日，查询时间区间T为5、10、20、50 周。

图4 给出了在内存存储数据情况下改变查询时间区间后的查询耗时对比。由图4 可以看出，当数据全部存在于内存时，TS_Pruning 算法运行时间开销最低，这是由于在查询条件相同的情况下TS_Pruning 算法扫描路径更少，TS_Mining 算法不需要多次迭代扫描数据集，因此相比Apriori 算法查询耗时约减少了2 个数量级，具有明显的效率提升。

图4 改变查询时间区间后的查询耗时对比Fig.4 Comparison of query time consumption after changing the query time interval

图5给出了在磁盘加载数据情况下改变查询时间区间后的加载与查询总耗时对比。由图5可以看出，查询所需数据需要从磁盘中加载到内存，基于F-Tree的算法相对于Apriori算法具有大幅的效率提升，但由于查询任务的耗时主要在数据加载到内存的过程中，因此TS_Mining与TS_Pruning算法的总耗时差别并不明显。对于twitter 数据集和blogs 数据集，设置查询阈值θ为10、20、50、100、200。图6给出了在twitter数据集和blogs数据集下的查询耗时对比，由两个数据集中的运行结果显示，TS_Pruning算法的查询效率高于Apriori算法。

图5 改变查询时间区间后的加载与查询总耗时对比Fig.5 Comparison of loading and total query time consumption after changing the query time interval

图6 改变查询阈值后的查询耗时对比Fig.6 Comparison of query time consumption after changing the query threshold

通过以上实验结果可以看出，本文提出的TS_Mining 算法和TS_Pruning 算法能够较好地适应不同需求的查询问题，在不同查询阈值和查询时间区间的应用场景下均能保持更好的查询效率。

为验证本文算法在实际应用场景中的可用性，除了算法查询时间外，还统计了基于Apriori 和F-Tree 算法的内存和磁盘存储开销。在所有数据及索引全部存储于内存的应用场景下，基于F-Tree 的算法的内存存储开销约为Apriori 算法的3 倍，如表2 所示。

表2 Apriori 与F-Tree 的内存存储开销Table 2 Memory storage overhead of Apriori and F-Tree

如表3 所示，当数据量较大需要在磁盘中进行存储时，F-Tree 索引的存储方式在磁盘存储开销上相对原始文本大小约有5 至6 倍的增长，但随着磁盘存储价格的不断降低，在外存存储的方式还是能够被接受的。对两类算法实时加载的最大内存消耗进行统计，如图7 所示，在实时加载数据的应用场景下，基于F-Tree 的算法内存消耗约为Apriori 算法的4 倍。然而，由于对于连续时间区间查询而言，只需逐次加载一个单位时间区间内的数据并进行挖掘，内存消耗仅与单位时间区间内数据量有关，与总数据集大小和查询条件的设置无关。

表3 F-Tree 磁盘存储开销Table 3 Disk storage overhead of F-Tree

图7 实时加载的最大内存消耗Fig.7 Maximum memory consumption for real-time loading

5 结束语

本文研究连续时间区间内的频繁词序列挖掘问题，通过改进后缀树结构提出基于频率树的快速频繁词序列挖掘算法。针对连续时间区间内的频繁词序列查询问题，设计改进的剪枝挖掘算法进一步提升频繁词序列挖掘效率。实验结果表明，本文提出的基于频率树的快速频繁词序列挖掘算法和改进的剪枝挖掘算法在不同的应用场景下的查询效率均明显优于传统Apriori 挖掘算法。后续将针对频率树的外存存储代价问题进行优化，通过压缩频率树索引和改进后缀树加载效率，进一步提高整体查询和加载效率。