深沟球轴承回转误差建模与分析
李 聪,王德伦
(大连理工大学机械工程学院,辽宁大连 116024)
0 引言
轴承目前被广泛应用于各类机械产品,例如高端精密加工机床等各种高端重大设备中[1-2]。轴承已经成为了机械设备的基础与核心部件,其可靠性和回转运动的精度与主机的可靠性和工作精度息息相关[3-4]。而轴承的回转精度又受到多种因素的影响。因此,建立轴承回转误差模型,研究各种因素对轴承回转精度的影响,对提高轴承回转精度,指导轴承设计制造与装配具有重要理论意义。
杨小高等[5]研究了加工误差因素对油膜轴承的影响。涂文兵[6]从表面波纹度的角度分析了对轴承振动的影响。张魁[7]以圆柱滚子轴承为研究对象,研究了元件波纹度对圆柱滚子轴承振动特性的影响。河南科技大学石文祥[8]研究了轴承旋转的精度,分析了滚道几何误差与轴承回转精度二者之间的关系。王宝坤,陈观慈等[9]建立了圆柱滚子轴承二自由度静力学模型,研究了轴承元件几何误差对轴承回转精度以及载荷分布的影响。吴柏华等[10]分析了工况条件对于轴承回转精度的影响。上述研究分析了多种影响因素对于轴承静态与动态精度的影响,但是大多是从三自由度轴承模型的角度对轴承回转精度进行分析,且对轴承的角摆误差分析较少,对于轴承各元件几何误差对于轴承回转精度影响研究较少。在建立轴承回转精度模型时大都对于轴承元件几何误差进行简化处理,或者直接将零件进行理想化建模,缺少对于真实几何误差对于轴承回转精度的研究。
综上,本文以深沟球轴承为例,基于轴承零件几何运动方程与力平衡方程,将轴承零件的物理属性、几何误差与工况载荷因素考虑在内,建立深沟球轴承六自由度回转误差模型。
1 轴承回转精度模型建立
1.1 轴承沟道几何形状描述
深沟球轴承的沟道曲面可以看作是滚道截面绕轴承轴线旋转得到的圆弧轮廓[11]。因此滚道的曲面轮廓上任一点Pij都可以通过3 个参数进行描述:圆弧点处的轴向截面角θ、圆弧点夹角φ与圆弧点处的曲率半径。因此,可以通过拟合实际误差滚道各截面的采样点来描述深沟球轴承滚道的几何形状。
设点Pij(xij,yij,zij)是轴承轴向截面滚道上的一点,如图1 所示。用测量仪对轴承滚道轮廓进行采样,得到其坐标值。设该截面的沟道曲率中心坐标为(a,b,c),则有:
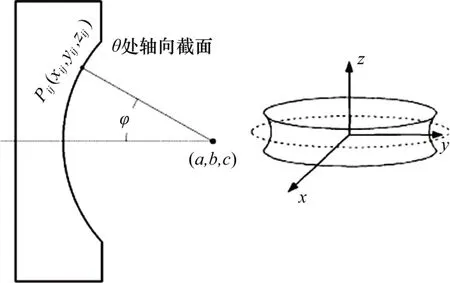
图1 轴承沟道拟合原理

式中:L为沟道曲率中心到外圈轴线的距离;θ为轴向截面的夹角;Z为沟道曲率中心在固定坐标系下的轴向坐标。
令Pij(xij,yij,zij)为在轴承(φ,θ)处截面沟道曲面处坐标,r为在该点处测得的曲率半径。再由上面求得的在轴承θ处截面的曲率中心坐标,便可得到误道曲面G的函数如下:
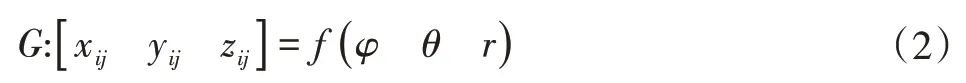
1.2 空间运动坐标系的建立
以外滚道建立全局固定坐标系Of Xf Yf Zf和内滚道建立局部坐标系On Xn Yn Zn,以滚动体圆心建立滚动体坐标系Og Xg Yg Zg,坐标系原点分别为Of, On, Og,如图2 所示。
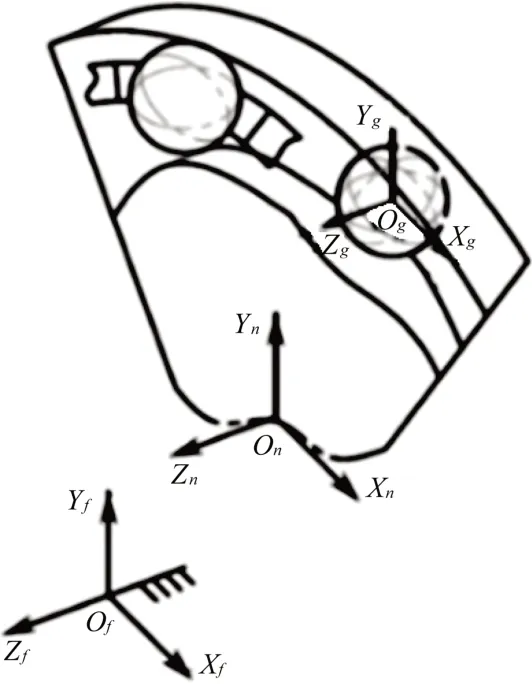
图2 轴承空间坐标系建立
1.3 滚道曲面建立
通过圆度仪测量得到滚道几何误差数据,对测量得到的数据点(θ,φ,r)进行数据处理,转化为参数平面与(x,y,z)对应关系,然后进行曲面拟合,如图4所示。

图3 内滚道几何误差检测
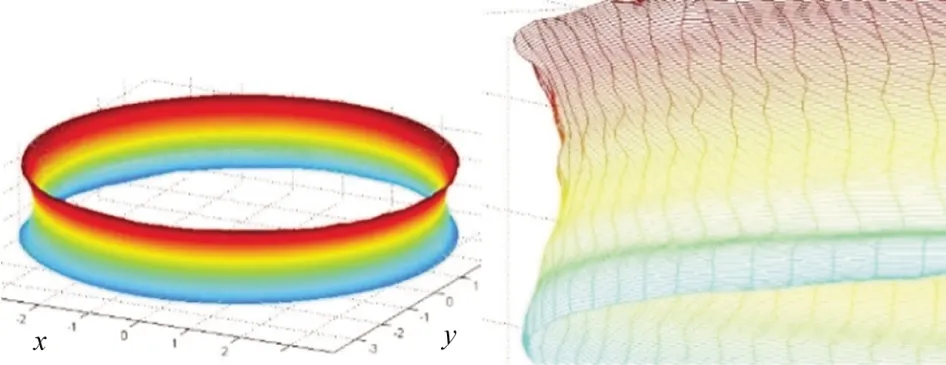
图4 内滚道误差放大1 000倍后滚道曲面

式中:Pij为各个网格点;Bi,3(φ)、Bj,3(θ)分别为节点向量φ、θ的3阶样条基函数。
滚道曲面及其法线如图5 所示。内滚道局部坐标系的坐标原点在固定坐标系下的方向矢量为ROn,在固定坐标系下点P的坐标可用下式表示:
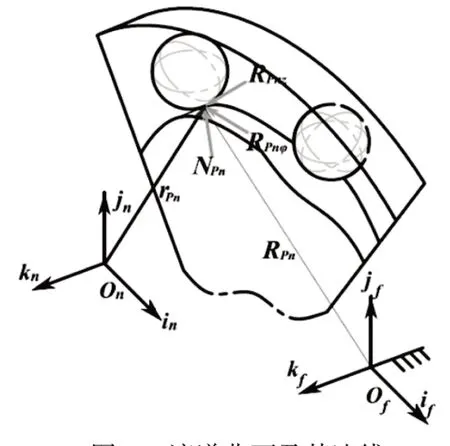
图5 滚道曲面及其法线
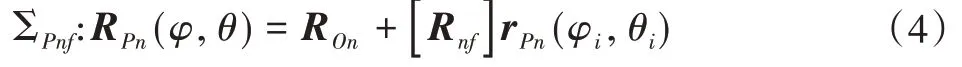
对上式求偏导,便可求得点P在两个方向上的切向量为:
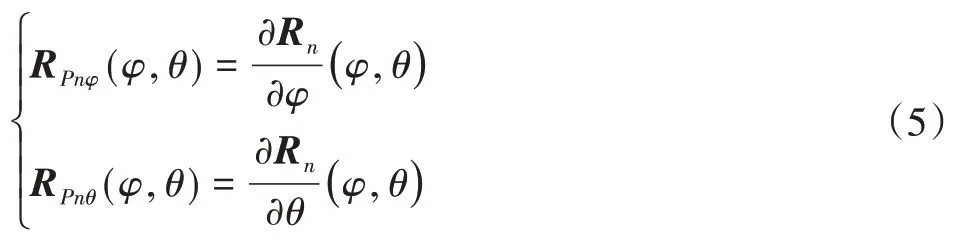
通过对两个切向量进行叉乘然后单位化,便可求得点P处的法向量如下:
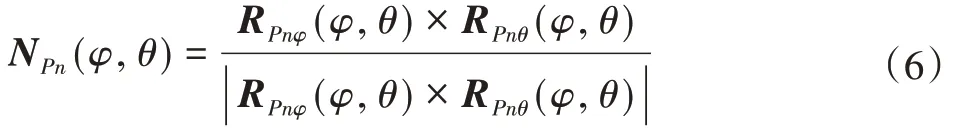
同样的方法对外沟道曲面进行曲面拟合。外沟道曲面在固定坐标系Of Xf Yf Zf下的误差曲面方程和以及任一点的法向量如下:
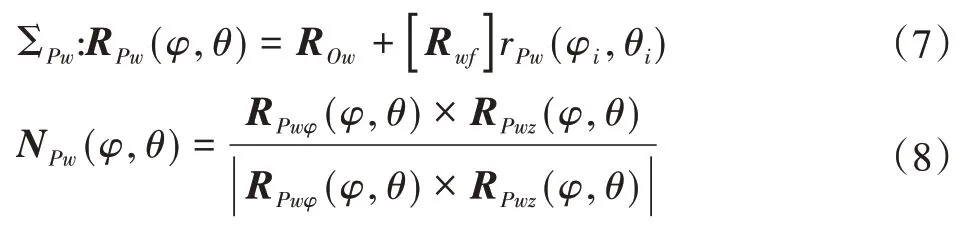
1.4 几何位移方程
(1)滚动体与外滚道位移方程建立
滚动体与外滚道位姿关系如图6 所示。基础坐标系Of Xf Yf Zf固定于轴承外滚道,外滚道曲面由前面的曲面拟合已知为ΣPnf,已知滚动体在基础坐标系下的初始位置为Rg(xg,yg,zg),由公式可求得滚动体与外滚道的近似接触角φ:
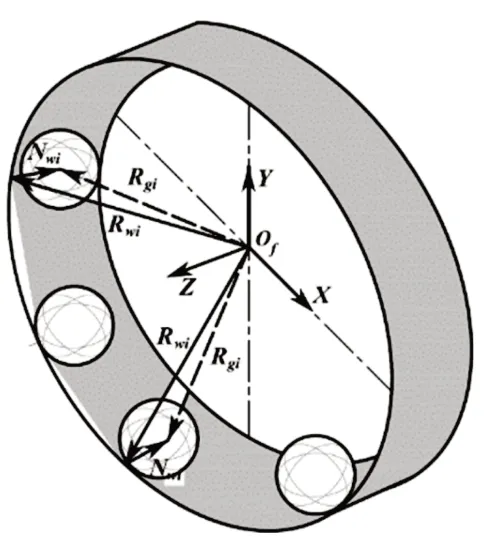
图6 滚动体与外滚道位姿关系
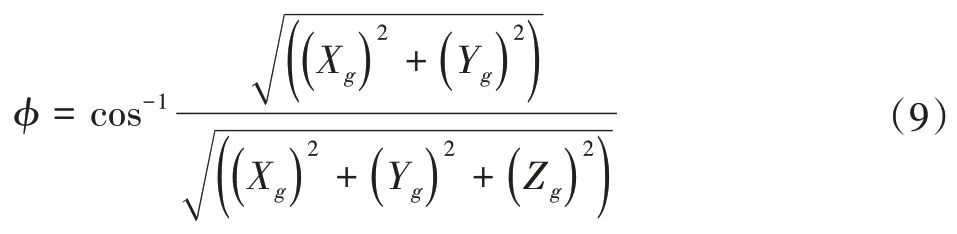
位置角θ:
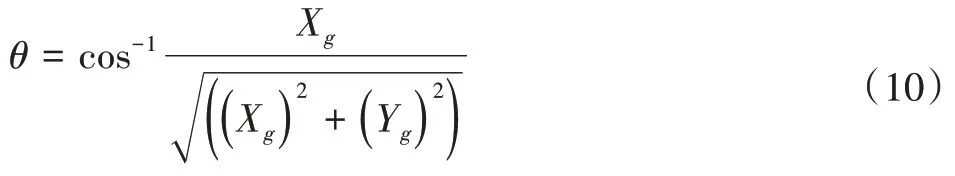
由近似接触角φ与近似位置角θ可在外滚道拟合曲面P搜索确定最大接触点Rw,定义接触位置变形量为δw,接触点的单位方向矢量为Nw,则滚动体与外滚道的位移方程为:
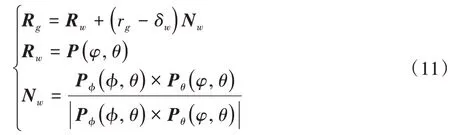
由方程可以求得δw,若δw<0,则滚动体与外滚道未接触,若δw>0,则滚动体与外滚道接触,且变形量为δw。
(2)滚动体与内滚道位移方程建立
滚动体与内滚道位姿关系如图7所示。
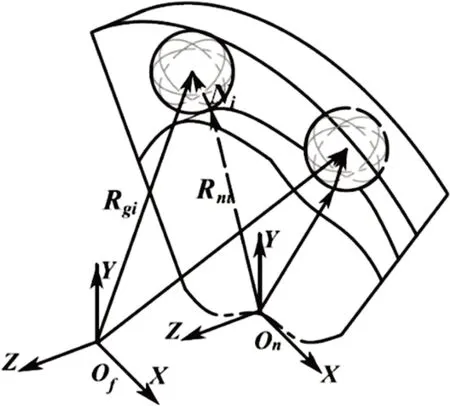
图7 滚动体与内滚道位姿关系
坐标系On Xn Yn Zn固定于轴承内滚道,内滚道曲面已知为ΣPnf。已知滚动体在基础坐标系下的位置为Rgf:(xg,yg,zg),根据坐标变换矩阵可求得滚动体在运动坐标系下坐标:

式中:Bfn为由基础坐标系向内圈运动坐标系的坐标变换矩阵;ROn为内滚道局部坐标系的坐标原点在固定坐标系下的方向矢量。
由下式可求得滚动体与内滚道的位置角θ:
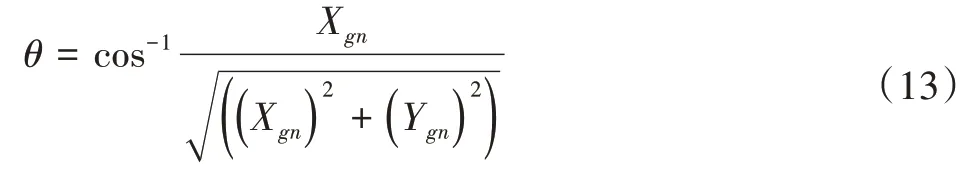
并可以求得内滚道在该位置角下在运动坐标系的曲率中心坐标(Xin,Yin,Zin),进而求得初始接触角φ:
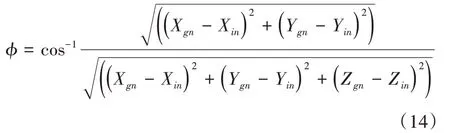
由初始接触角φ与初始位置角θ可在内滚道拟合曲面ΣPnf搜索确定最大接触点Rnn,定义接触位置变形量为δn,接触点的单位方向矢量为Nnn,则滚动体与内滚道的位移方程为:
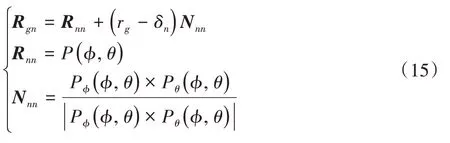
由方程可以求得δn,若δn>0,则滚动体与内滚道接触,且变形量为δn。
滚动体与接触点在运动坐标系On Xn Yn Zn下的单位方向矢量为Nnn,通过坐标变换方程转化为固定坐标系Of Xf Yf Zf下的单位方向矢量为Nn:

式中:Bnf为由内圈运动坐标系向基础坐标系的坐标变换矩阵。
(3)保持架与滚动体位移方程
本部分只考虑保持架兜孔与滚动体间的法向力与摩擦力,并且假设保持架始终保持着理想转动,保兜孔与滚动体的位置关系如图8所示。
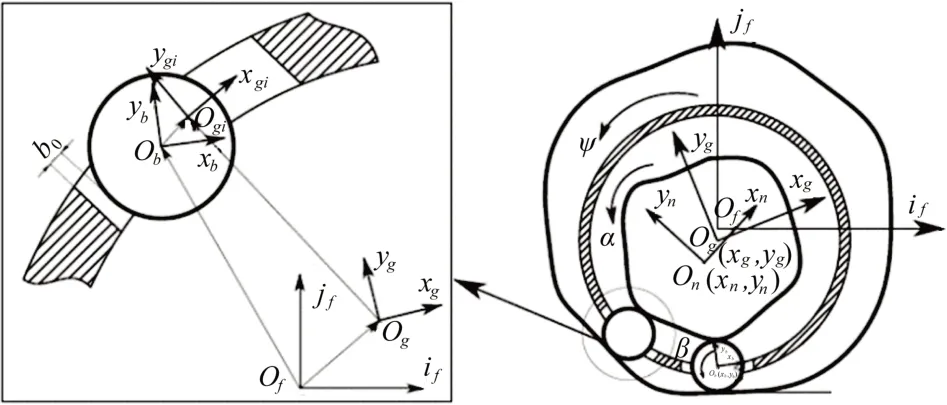
图8 保持架兜孔与滚动体的位置关系系
保持架质心Rb、滚动体质心Rgi和兜孔质心Rhi三者的几何位移方程如下:

兜孔与滚动体i在接触点的法矢为两者质心的矢量差Nb,变形量δbi等于兜孔半径与滚动体半径差减去滚动体质心与兜孔质心的距离的差值,且变形量δbi等于结果的绝对值,如下所示:

式中:Rb为保持架质心位置;rb为保持架兜孔半径;rg为滚动体半径;Rp为兜孔半径与滚动体半径差值减去滚动体质心和兜孔质心的距离的值;δbi为接触点处的弹性变形量。
1.5 受力平衡方程
内滚道与滚动体受力如图9 所示。基于前文的几何位移方程,建立内滚道和滚动体的力平衡方程组。
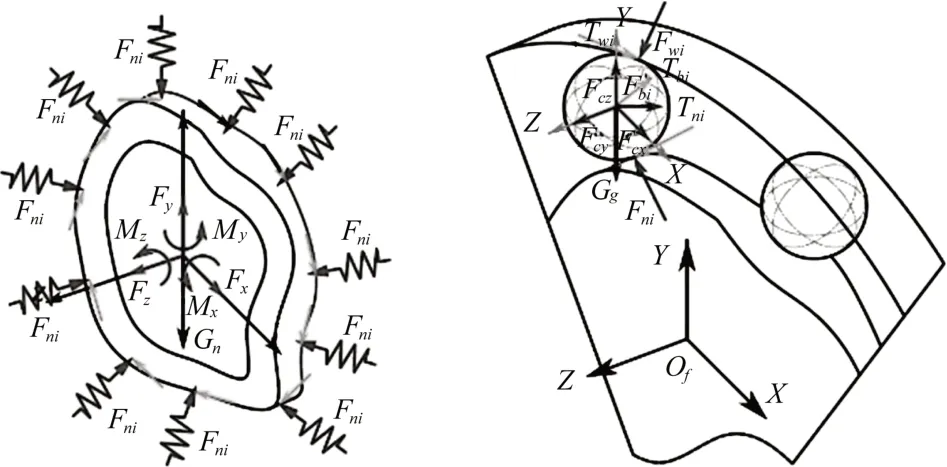
图9 内滚道与滚动体受力示意图
滚动体与内外滚道之间的接触刚度Kn可由下式求得:
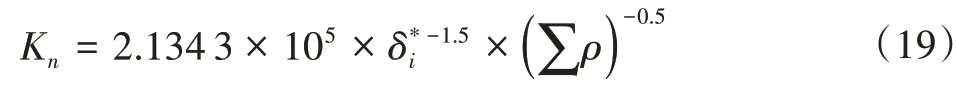
式中:为根据曲率差函数值通过查表得到的参数;Σρ为曲率和函数值。
由几何位移方程可求得各滚动体与轴承内外圈的接触情况与变形量δw、δn,则可求得各滚动体与内外滚道的法向接触力与摩擦力:

根据位移方程求得各接触位置的变形量,便可分别列出滚动体与内滚道的力平衡方程组。某一滚动体i受内外滚道和保持架的作用力,建立该滚动体的力平衡方程如下:
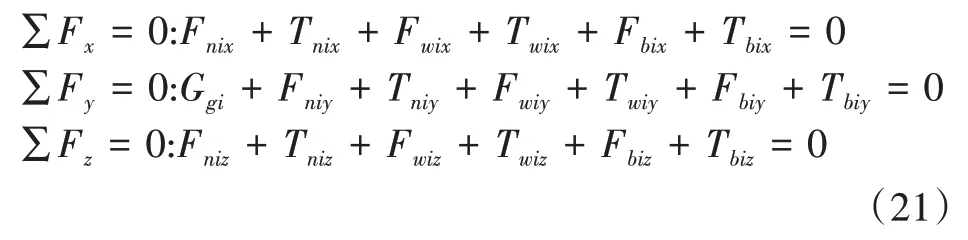
同理,在固定坐标系下,内滚道的力平衡方程如下:
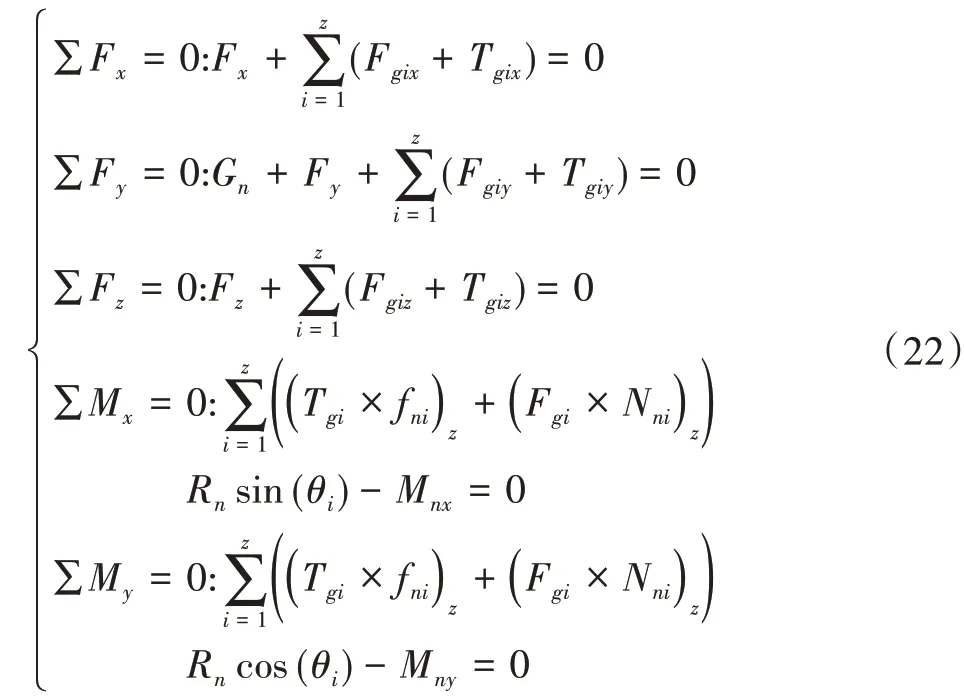
式中:(Fnx,Fny,Fnz)(Fwx,Fwy,Fwz)分别为滚子与内外滚道接触力在固定坐标系下X、Y、Z方向的分力;(Tnx,Tny,Tnz)(Twx,Twy,Twz)分别为滚子与内外滚道摩擦力在固定坐标系下X、Y、Z方向的分力;(Fx,Fy,Fz,Mx,My)为内圈的载荷;Fg为滚子对内滚道的反作用力;Tg为滚子对内滚道的反向摩擦力;Rn为滚子与内滚道接触点的矢量在XY平面投影的长度;θi为各滚子的位置角。
2 模型求解
上述方程组中的滚动体的位置Rgi与内外沟道的误差曲面ΣP以及滚道在固定坐标系下的位姿有关,而且载荷接触刚度Kn为非线性,因此无法求解精确数值解,需要通过优化求解,过程如下。
(1)首先拟合得到滚道误差曲面的拟合方程Σpw和ΣPnf,并给定滚动体初始值(xgi,ygi,zgi)与内滚道的初始位姿( xn,yn,zn,αn,βn)。
(2)通过轴承各元件间的位移方程,求解出滚动体质心位置Rgi以及内滚道的质心位置Rn,各滚动体与内外圈滚道和保持架的接触情况,发生接触位置处的变形量与法矢(δni,Nni,δwi,Nwi)。
(3) 根 据 (2) 求 得 的 接 触 变 形 量 与 方 向(δni,Nni,δwi,Nwi),求得接触力与摩擦力,代入滚动体受力平衡方程,计算力不平衡量,根据平衡量修正滚动体位姿参数(xgi,ygi,zgi),返回第(2)步。当不平衡量满足精度要求时停止迭代。
(4)第(3)步的所有滚动体不平衡量精度均满足要求后,根据位移方程,确定滚动体与内滚道的接触变形量与接触点法矢(δni,Nni)。
(5)根据(4)求得的变形量与方向(δni,Nni)求得各滚子对内圈的接触力与摩擦力,代入内圈受力平衡方程,根据力不平衡量修正内圈位姿参数( xn,yn,zn,αn,βn),返回第(2)步。直至内圈不平衡量达到求解精度,最终计算求得的内圈位姿即为该角度下的求解结果。
3 算例分析
以6312 深沟球轴承为例,其参数如表1 所示。通过改变滚动体直径误差与径向游隙研究对回转精度的影响,评价指标为基于不变量的评价方法[12]。使用Matlab 编写模型程序,计算得到轴承回转精度情况。
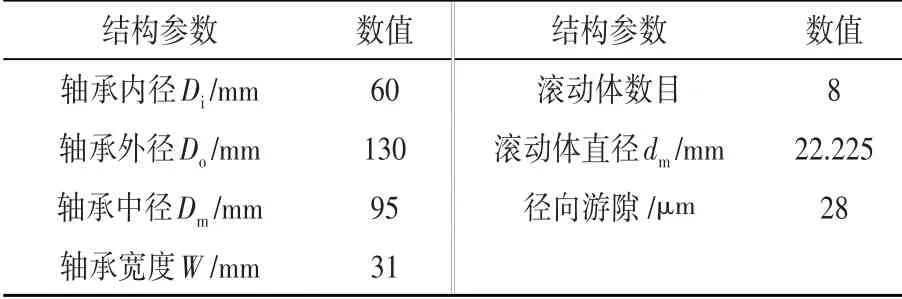
表1 6312轴承参数
(1)不考虑元件误差纯径向载荷回转精度
不考虑元件误差纯径向载荷回转精度如图10 所示。再由作图法得到轴承在承受纯径向载荷下的轨迹图,得到理论值,与程序计算结果进行对比,如表2所示。
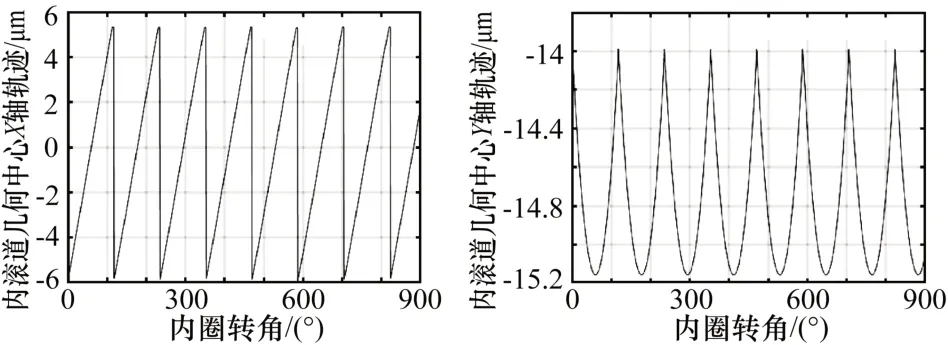
图10 不考虑元件误差纯径向载荷回转精度

表2 轴承回转精度计算值与理论值比较
(2)轴承滚动体直径误差对回转精度的影响
本节主要讨论多个滚动体存在直径误差时,滚动体的不同排布方式对于轴承回转精度的影响。该部分将8个滚动体半径误差分为4 组,分别为-2 μm、-1 μm、1 μm、2 μm,滚动体进行不同的排布如表3所示。
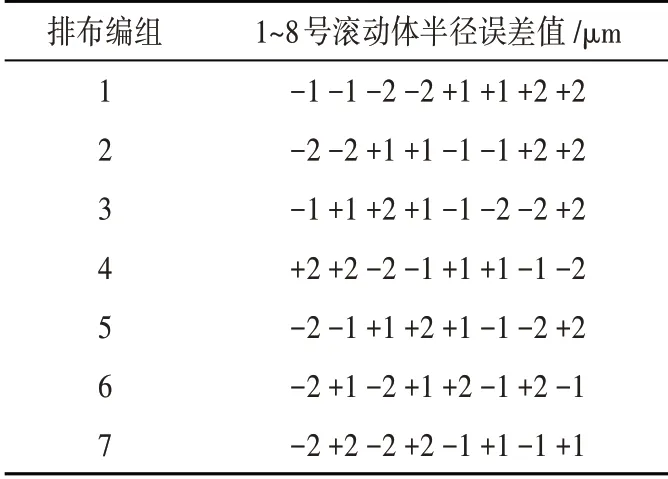
表3 滚动体误差值及其排布方式
计算得到不同排布方式下轴承的回转精度,如图11所示。图中,δR0为最小球面像圆与拟合轴线的半锥顶角,来表示角摆误差的大小;rRc表示径向平移误差的大小;ΔRu表示轴向平移误差的大小。由图可知,排布7的排布形式的回转精度远大于其他排布形式,当滚动体存在误差时,滚动体排布对轴承回转精度存在显著影响,合理的滚动体排布方式可使轴承角摆误差相较于最大角摆误差减小83.3%,可使轴向平移误差相较于最大轴向平移误差减小23.5%,径向平移误差相较于最大径向平移误差减小71.4%。
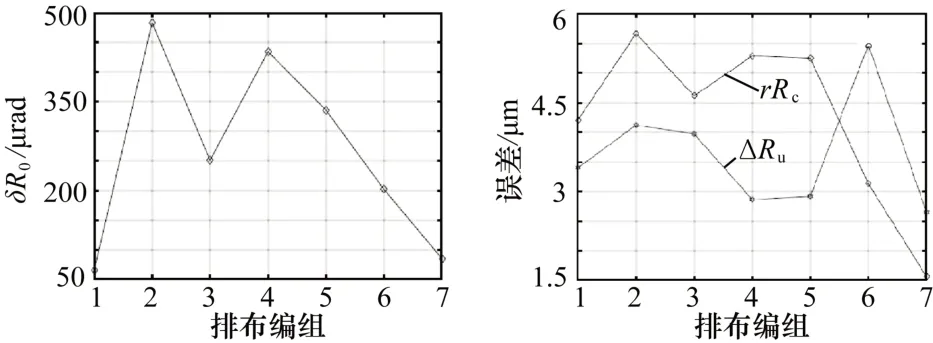
图11 滚动体排布方式对不变量精度的影响
(3)轴承径向游隙对回转精度的影响
本节主要讨论径向游隙对于轴承回转精度的影响,以6312轴承为研究对象,在准静态情况下,轴承同时承受轴向预紧载荷100 N,径向载荷300 N,通过将径向游隙由4 μm 增加到28 μm,研究径向游隙对回转精度的影响。得到的结果如图12所示。整体来看,随着径向游隙的增大,轴承回转精度变差,径向游隙为20 μm 时的角摆误差比10 μm 时增大了890%,径向平移误差增大了926%,轴向平移误差增大了434.4%,且随着游隙的等比例增加,轴承回转精度的降低越来越明显,轴承回转精度迅速变差。
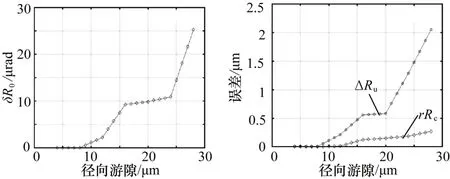
图12 径向游隙对不变量精度的影响
4 结束语
本文以深沟球轴承为研究对象,基于轴承零件几何位移方程与力平衡方程,综合考虑了零件物理属性、几何误差与工况载荷的耦合效应,建立了深沟球轴承六自由度回转误差模型。本文通过算例分析滚动体直径误差和轴承径向游隙对轴承回转精度的影响得到以下结论:多个滚动体存在误差时,滚动体排布对轴承回转精度存在显著影响,合理的滚动体排布方式可使轴承角摆误差相较于最大角摆误差减小83.3%,可使轴向平移误差相较于最大轴向平移误差减小23.5%,径向平移误差相较于最大径向平移误差减小71.4%;随着径向游隙的增大,轴承回转精度变差,径向游隙为20 μm 时的角摆误差比10 μm 时增大了890%,径向平移误差增大了926%,轴向平移误差增大了434.4%,且随着游隙的等比例增加,轴承回转精度的降低越来越明显,轴承回转精度迅速变差。

