基于二维码和图像处理的新型加密算法研究*

乔婉妮

（兰州交通大学电子与信息工程学院，兰州 730070）

0 引言

二维码又称二维条码，最常见的形式是QR Code，QR 全称Quick Response，是一个近几年来移动设备上十分流行的一种编码方式，它能比传统的Bar Code 条形码储存更多的信息，也能表示更多的数据类型。

二维码（2-dimensional bar code）是在一维码的基础上，使用某种特定的几何图形按照一定的规律在水平和垂直方向存储数据符号信息的黑白相间图形[1-2]，二维码具有可表示汉字图像等多种文字信息、存储信息容量大、可靠性强等优点。使用构成计算机内部逻辑的“0”和“1”位流的概念，对应于二进制系统的各个集合对象来表示文本数字信息[3-4]。通过图像输入装置或光电扫描装置实现自动信息处理。由于其具有高密度、大容量等特点，因此可以用来表示发送内容[5-7]。它还具有条码技术的一些共性，如每种码制有其特定的字符集、每个字符占有一定的宽度、具有一定的校验功能等。同时还具有对不同行的信息自动识别功能及处理图形旋转变化点。QR 码已在社交生活的许多领域中得到广泛使用，并已成为连接现实和虚拟的最强大工具之一。

截止到目前，有关QR 码信息隐藏技术的研究很多。但是，在国内外，大多数方法都是通过加密算法或比较和识别大量私钥来编码和修改基础数据的[8]。前者具有低便捷性，后者由于解析速度慢、识别时间长和成本高而难以使用。基于以上问题，本文设计了一种高度可移植、快速、可靠的二维码信息加密系统和解密系统。

国内市场上功能类似的商业设计主要是通过数据库检索的方式隐藏信息，即通过QR 码携带一段字符串，用户端识别QR 码的时候只能识别字符串。企业端通过地址字符串搜索预先建立的信息数据库。通过使用用户的个人信息来实现加密用户信息的目的。这种方法本质上不会加密任何信息。这意味着，只要访问数据库，所有用户的个人信息实际上就是完全公开的。这种方式存在巨大的安全缺陷。

本文介绍了一种新的加密算法。该算法使用双方都必须同意的私钥，首先将要发送的数据编码为QR 码，然后使用简单但非常有效的过程对QR 码进行加密。将私钥（KeyQR）和接收方数据（DataQR）进行异或运算以生成伪装QR 码，并建立数据读取设备。私钥匹配后以恢复有效信息。在确定了固定点之后，根据私钥设置将QR 码的非定位区域划分为m块等面积四边形，并确定分割区域的等效点，即相对中心点。根据等价类原理，分段的m块等距四边形是根据其位置到等效点的弧之间的距离进行校准，每组分配相同值的四边形都有4个块。通过选择左手或右手模式，等效的四边形位置被交换以形成新的图像。

1 处理

1.1 QR码的基本结构

QR码是一种黑白图形，它在具有特定几何图案的平面（二维方向）上被巧妙的编码以记录数据符号信息。构成计算机内部逻辑的“0”和“1”为流的概念通过使用对应于二进制的多个几何形状来表示文字和数字信息，这些形状由图像自动读取设备或光电扫描设备输入。自动信息处理具有条形码技术的一些共性，每个代码系统都有自己特定的字符集。每个字符占据一定的宽度，其具有一定的检查功能，同时还具有针对不同行信息的自动识别功能，并处理图形的旋转变化点。QR码基本结构如图1所示。

图1 QR码基本结构

1.2 密码分组链接模式（Chipher Block Chaining）

密码分组链接模式（CBC）是将前一个密文分组与当前明文分组的内容混合起来进行加密，这样就可以避免明文被主动攻击。当加密第一个明文分组时，由于不存在“第一个密文分组”，因此需要事先准备一个长度为一个分组的比特序列来代替“前一个密文分组”，这个比特序列称作初始化向量（Initialization Vector），每次加密时都会随机产生一个不同的比特序列来作为初始化向量。在CBC 模式中，首先将明文分组与前一个密文分组进行异或操作，然后再进行加密，如图2所示。

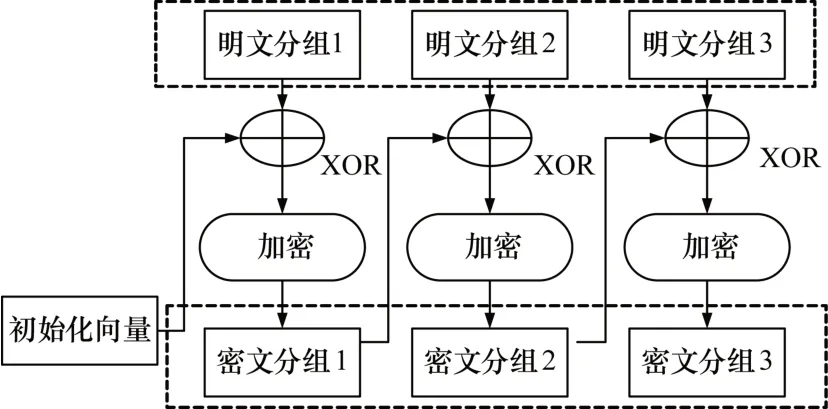
图2 CBC模式加密流程

1.3 算法流程

预传播信息用于生成QR 码图像，将QR 码放置在识别帧中，然后获得图像帧。进行包括灰度和中值滤波器的图像预处理，并且通过识别位置点来获得正方形图像。通过按位进行异或计算以生成加密图像TransmissionQR。最后伪装后的图像由识别编码算法相对应的解码算法处理。QR解码过程完成后，获得预传播信息。算法流程如图3所示。

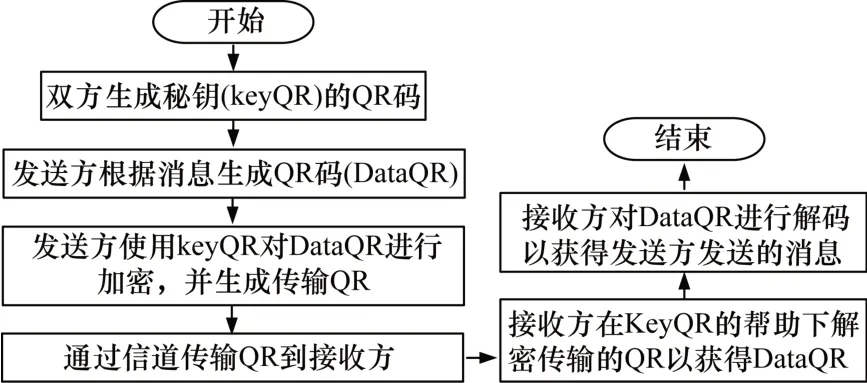
图3 算法流程

1.4 加密数学模型

异或操作具有可逆性的独特属性。由于异或算法是按位执行的，因此运算速度非常快，加密和解密耗费的时间也很短。这使得异或算法在加密和解密算法当中十分受欢迎。

1.4.1 证明1

下面证明系统可以从TransmissionQR 和KeyQR 中生成DataQR。用“D”代表DataQR，“K”代表KeyQR，“T”代表TransmissionQR。

第一步：传送方。TransmissionQR 由DataQR 和Key-QR二者按位异或生成，因此，T=D⊕K。

第二步：接收方。DataQR 由TransmissionQR 和Key-QR 通过异或产生。令G代表接收端产生的QR。则G=T⊕K，并且T=D⊕K，因此G=G(D⊕K)⊕K，由于异或运算是相关的，有G=D⊕(K⊕K)。由于元素自身异或等于0，化简为G=D⊕(0)。元素与0 进行异或值不变，最终化简为G=D。

这证明了上面的假设，即DataQR 可以从TransmissionQR和KeyQR生成，反之亦然。

1.4.2 证明2

下面利用矛盾法证明只能有一个私钥可以解密TransmissionQR 以重新生成DataQR。

令K1为第一个对QR 进行解密以生成DataQR 的私钥KeyQR。因此，T⊕K1=D，在等式两边取T的异或：

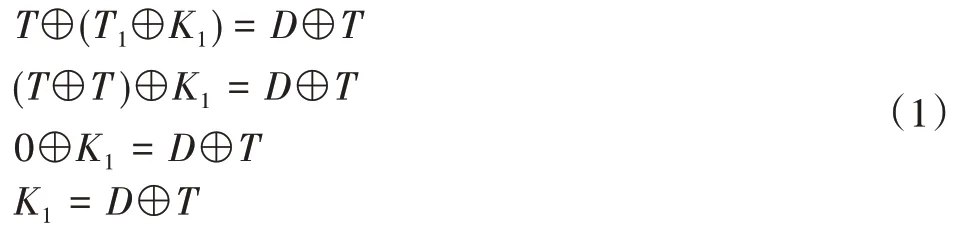
令K2作为第二个KeyQR，它对TransmissionQR 进行解密以生成DataQR。因此，T⊕K2=D，同样在两侧取T的异或：

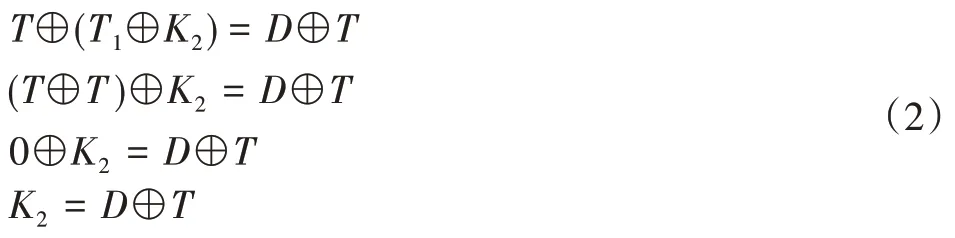
然而式（1）和（2）与假设的K1和K2是不同的值相矛盾。因此通过矛盾，证明K1和K2是相同的密钥，因此只有一个密钥可以解密TransmissionQR 来生成DataQR。

1.5 算法与QR码结合

由于QR 码是一幅图像，而图像是像素的集合，因此可以分别对每个像素进行操作以分别生成TransmissionQR 和DataQR。QR 码是黑白像素的集合，可以使用此图像的二进制形式将黑色表示0，将白色表示为1。这将会确保按位异或的时候可以应用于每个像素，以此分别生成TransmissionQR 和DataQR。像素级异或的图形表示如图4所示。

2 非对称加密算法

2.1 RSA概述

RSA 是一种传统的非对称密钥加密算法，它是由RIRivest、AShamir 和M Adleman 在1978 年在MIT 上提出的。RSA 是基于大素数证书分解的指数函数，被认为是陷阱门单向函数。之所以将其称为“活板门”，是因为一旦系统知道某个“活板门”信息，其逆函数就很容易被计算。之所以称它是单向的，是因为其在一个方向上易于计算，而在另一个方向上却难以计算。在RSA 中，纯文本和密文被视为从0～n-1 的整数（通常n的大小为1 024 ）。

2.1.1 生成Pri-Pub密钥对

（1）选择两个素数整数p和q（每个1 024位），其中p≠q；

（2）计算模量n=q·p；

（3）计算n′=(p- 1)·(q- 1)并找出私有指数，使其gcd(d,n′) = 1；

（4）计算公共指数e：e·d= 1(mod(p- 1)·(q- 1))，它是乘法的逆运算；

（5）因此，公钥为（n，e），私钥为（n，d）。

2.1.2 加密和解密

为了加密密文，首先将明文表示为正整数M。然后使用公钥（n，e）进行计算，E(M) =Me(modn)，然后发送方将E（M）发送给接收方。解密密文类似于加密。接收方使用自己的私钥（n，d） 进行计算，D(E(M)) =E(M)d(modn) =M。然后可以从整数M中获取到明文。

2.2 RSA算法的实施

2.2.1 密钥生成

（1）生成512位的随机素数

生成一个512 位长的奇数随机数后使用RabinMiller算法[80]检验测试素数。ACK=1 表示这个数字是素数，生成出一对512位的素数p和q。

（2）生成公钥（n，e）和私钥（d，e）

计算n，n=p·q，Φ(n) =(p- 1)·(q- 1)。计算e时，使用欧几里得算法找到GCD，为了计算公钥，状态Inc_PubKey 将 变 量PubKey+1，状 态Cherck_Large 查 找Phi 和PubKey 中较大的一个。为此，利用欧几里得算法通过重复减法，通过状态GCD_CAL_MOD 和GCD_CAL_MOD2 计算出GCD。当较小的数（除Phi 和PubKey 之外）减少到0 时，就会找到GCD。状态GCD 会检查tgcd 是否等于1，如果等于1，则当前状态返回到Inc_pubKey状态。

状态Prv_cond 检查余数是否为0。如果不是，则k+1，当前状态返回到Prv_Mul 状态。这种情况一直持续到(1+(k·φ(n)))对于k的某个值完全能被e整除。计算出的d对应的值是私钥指数d。一旦计算出公钥指数e和私钥指数e就可以分别进行加密和解密。

2.2.2 加密

计算公式为：c=me(modn)

式中：m为待加密的明文或消息；e和n分别时密钥生成模块生成的公钥指数和模。

因为n的值非常大，所以不能计算这么大的值，在下文中将解决这一问题。

（1）模块化的乘法

模乘意味着计算(A·B)modn。实现模乘有各种技术。32 位乘法运算采用移位加技术。使用32 位乘法是因为灰度图像的像素值不能大于255。当k=32 时，被乘数和乘数都是k位二进制数。模块化乘法算法如下：

P=0

For i=0 to k-1

P = 2P + A*Bk-1-i

P=P mod n

Return P

（2）模幂运算

密码c=me(modn)只是重复的模积。模块化产品（A·B）modn被部署在重复模乘技术中以执行模求幂。用一个例子来解释重复模乘技术：

令m=85，e=5，n=497。

对于e′= 1,c′=(1× 85)mod497= 85mod497= 85；

对于

e′= 2,c′=(85× 85)mod497=7 225mod497= 267；

对于

e′= 3,c′=(267× 85)mod497= 22 695mod497= 330；

对于

e′= 4,c′=(330 × 85)mod497= 28 050mod497= 218；

对于

e′= 5,c′=(218× 85)mod497= 18 530mod497= 141。

（3）解密

与加密不同，这里的私钥本身值很大。因此，采用左向右二值法，假设d为k位长，解密算法如下：

输入：c，d，n

输出：Decmg:= cd(modn)

if dk-1= 1，then Decmsg=c else Decmsg=1

for i=k-2

Decmsg =(Decmsg*Decmsg)mod n

if di= 1,then Decmsg =(Decmsg*c)mod n

Return Decmsg

2.3 RSA算法的改进

利用文献[80]中提到的方法来对3 个素数因子进行加密，并消除密钥中的n。通过加入3 个素数因子的方案，其优点是减少了素数因子的长度，但是却增加了算法中素数因子的总个数，通过本文的消除密钥中n的设计后，可以让破坏者不轻易的破解密码，因此提高了系统的安全性。本文设计的算法共包含3 个部分，分别是：产生内部密钥、加密信息以及解密信息。

（1）步骤1：生成密钥

选择3个素数a1、a2、a3，a1≠a2≠a3。计算三者的乘积n=a1×a2×a3，得到欧拉函数：

φ(n) =(a1- 1) ×(a2- 1) ×(a3- 1)

随机选择一个整数k1，使得：

GCD(k1,φ(n)) = 1且n≤k1≤φ(n)

根据a1、a2、a3的大小关系，计算出X来替代n。

如果a1＞a2＞a3或者a1＞a3＞a2，解X得：

GCD(X,n) = 1,n-a1＜X＜n

如果a2＞a1＞a3或者a2＞a3＞a1，解X得：

GCD(X,n) = 1,n-a2＜X＜n

如果a3＞a1＞a2或者a3＞a2＞a1，解X得：

GCD(X,n) = 1,n-a3＜X＜n

将求得的X代入下式中，求解k2：

k2=k-11Mod(X)

此时，私钥是(k2，X)，公钥是(k1，X)。

（2）步骤2：加密消息

发送方通过私钥(k2，X)来加密消息M，其公式为：

C=Mk1Mod(X)

式中：C为加密后产生的密文。

（3）步骤3：解密消息

接收方通过私钥(k2，X)来解密密文C：

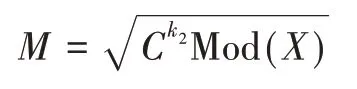
式中：M为加密前的消息。

改进RSA算法的加密步骤如图5所示。

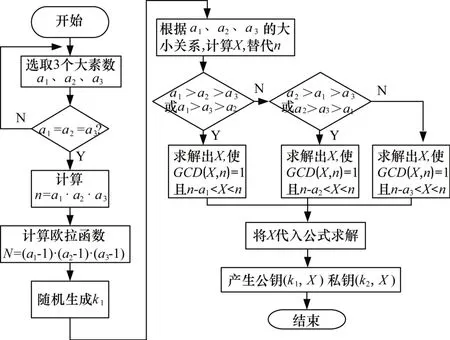
图5 改进RSA算法的加密步骤

通过用X替换n成功消除掉了n。由于攻击方无法通过X分解得到a1、a2、a3，这使得算法变得更加难以被破解。在加强安全性的另一方面，本文通过添加一种新的加密手段来加密RSA 算法，但是这种方法具有局限性，即只能用于只有二因子的RSA 算法中，其他类型的RSA算法无法使用，这也是后续需要改进的方面。

下面进行复杂度的分析。密钥生成算法根据a1、a2、a3的大小和复杂度o(2φ(n))以及加密算法的时间复杂度o(k1)，添加替换n的X的计算。 解密算法将平方根函数添加到模块化扩展函数的输出中。这是因为二次运算的时间复杂度是固定的序列所以解密算法的时间复杂度是o(k2)。

3 算法功能演示

让双方都接受私钥KeyQR，如图6 所示。扫描二维码后将不会得到正确信息，并弹出如图7所示的界面。

图6 私钥KeyQR

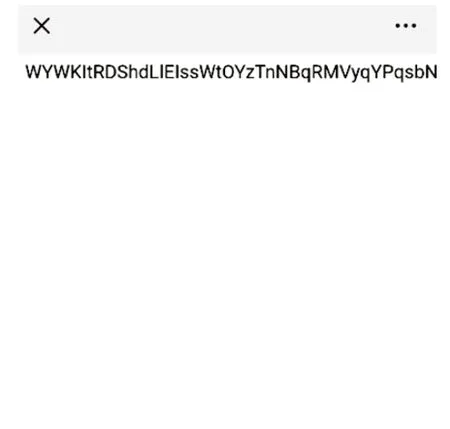
图7 通过扫描演示二维码获得的信息

将“username:aaa@aaa.com password：qweasdzxc”作为传递信息写入DataQR 中，如图8 所示。通过加密后传输的QR如图9所示。

图8 发送的数据DataQR

图9 TransmissionQR

最终接收方解密后的QR 如图10 所示。对TransmissionQR 码进行图像处理，并读取正确的信息“username:aaa@aaa.com password：qweasdzxc”，如图11所示。

图10 RetrievedQR

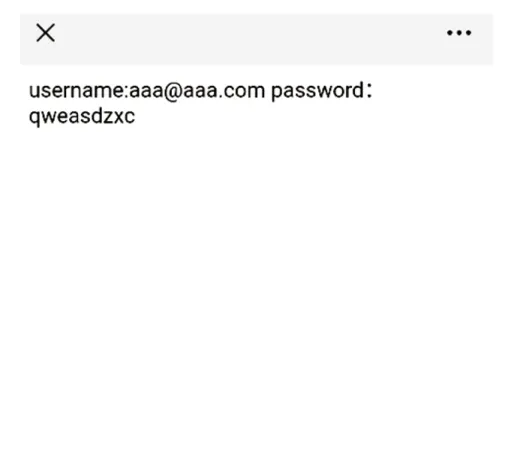
图11 QR码信息还原示例

4 结束语

本文提供并实现了一种基于国家标准代码系统的特殊QR 码加密算法。提出了一种将图像几何处理与QR 码信息加密相结合的新思路。该算法的加密级别可以根据用户自己的要求灵活更改。基本功能是只有特定的扫描读取系统才能读取加密的二维码中有效信息，而传统的读取系统只能获取加密的加密信息。本文算法考虑生成大小为128×128 像素的QR 码。加密的KeyQR 中的每个像素都有两个选择：黑色和白色。因此对于128×128 像素，有2（128×128）个选择。任何现代计算机都需要花费比Universe 更长的时间来生成和检查所有的组合，以找出正确的KeyQR。因此算法的安全性受到时间的限制。未来的工作中，尝试添加一些本地物理信息。为了使识别端通过物理信息匹配而不是内置密钥获得密钥，以此方法降低生产成本和技术门槛。