基于振动信号分析的水工金属闸门状态识别方法

杨 军，刘鹏鹏，漆玉龙，胡仲明

（1.国能大渡河大岗山发电有限公司，四川 雅安 625400；2.成都大汇物联科技有限公司，四川 成都 610000）

1 引言

水工金属闸门是水利工程中的关键设备，是完成水利泄洪功能、保障水工建筑物使用效果的重要组成，其运行状态优劣直接影响到整个水利工程，甚至引起安全事故，对流域内人民和生命财产安全造成巨大影响[1]。因此开展水工金属闸门状态监测及状态识别研究对于提高水工金属闸门的安全性、可靠性及可维护性具有重要意义。

针对水工金属闸门的状态监测目前多采用应变传感器、压力传感器、振动传感器、倾角传感器、声发射传感器等[2]，其中振动监测能够直观反应闸门状态，具有快速性和状态变化的灵敏性等优点，是未来水工金属闸门状态监测的主要发展方向。水工金属闸门在流激作用下产生的振动信号比较复杂，传统方法进行振动信号分析具有一定难度，机电装备振动信号分析方法给水工金属闸门状态识别提供思路。针对水工金属闸门振动信号复杂多变、且耦合性较强的特点，一般基于振动信号的状态识别需经信号分解、特征提取、状态识别等过程。信号分解是将水工金属闸门耦合性较强的振动信号分解为一系列易于分析的信号分量，常见的信号分解方法包括经验模态分解、局部均值分解、变分模态分解、集合经验模态分解等[3]，各种方法各有优势。其中经验模态分解方法容易造成信号混叠，变分模态分解方法必须提前确定信号中心频率，预估信号分量个数，分解过程无法自适应。EEMD充分利用了高斯白噪声的均匀辅助作用，通过在信号中加入高斯白噪声，改善信号极值点分布，能够有效避免信号模态混叠，同时分解过程完全自适应具有显著优势。

在特征提取方面，信息熵理论被越来越多地应用于振动信号的状态特征量化提取，其能够表征非线性信号的复杂性和平稳性，相比于具有统计意义的时域特征、频域特征等，具有更精细的特征刻画能力[4]。

在状态识别方面，以神经网络为代表的智能分类算法在传统机电装备故障诊断中得到了广泛应用和验证，可以为水工金属状态识别提供借鉴。传统的识别算法包括BP神经网络、支持向量机、极限学习机等[5]；同时随着技术的发展，例如卷积神经网络、堆栈自动自动编码机等深度学习算法也获得应用；同时，模糊逻辑、模糊推理也被证明具有较好的识别效果。但是以上方法各具优势，同时具有各自缺点，充分利用神经网络的数据学习能力和模糊逻辑的推理能力，可形成自适应神经模糊推理系统（ANFIS），能够兼具神经网络和模拟推理的优势，形成一种有效的状态识别方法[6]。

2 算法模型

2.1 集合经验模态分解

EEMD充分利用了高斯白噪声的均匀辅助作用，通过在水工金属闸门原始振动信号加入高斯白噪声，改善信号极值点分布，有效避免信号模态混叠问题，算法具体步骤如下[3,7]：

（1）进行参数初始化，初始化白噪声添加次数M。

（2）设水工金属闸门原始振动信号为x(t)，加入第m次白噪声后获得的振动信号为xm(t)=x(t)+βwm(t)，其中wm(t)为加入的白噪声，β为幅值系数，并初始化m=1。

（3）对于信号xm(t)，进行EMD过程，即针对xm(t)利用样条曲线求取其上包络线和下包络线的均值曲线，并以此计算信号xm(t)和均值曲线的差值，记为

（6）则针对在原始振动信号中每次加入白噪声后的信号，重复以上过程（2）~（5）；即如果m没有达到设定次数M，则m=m+1，重复过程（2）~（5），直到达到设定的白噪声添加次数，则可以获得M组IMF分量，即，i=1，2，...，I；m=1，2，...，M。

（7）针对每次加入高斯白噪声获得的IMF分量进行总体平均，就可获得最终的EEMD分解结果，则最终获得的EEMD分解结果为：

其中Ci(t)，i=1，2，...，I为EEMD分解所获得的最终IMF分量。

2.2 功率谱熵提取

针对水工金属闸门振动信号经过EEMD获得的一系列IMF分量Ci(t)进行功率谱熵特征提取，从功率谱分布角度对各IMF分量的信号特征进行量化。假设某一分量为Ci(t)=（x1，x2，...，xN），对其进行傅里叶变换获得F（ω）=FFT（Ci(t)），进一步获得其功率谱为：

进一步功率谱熵可表示为：

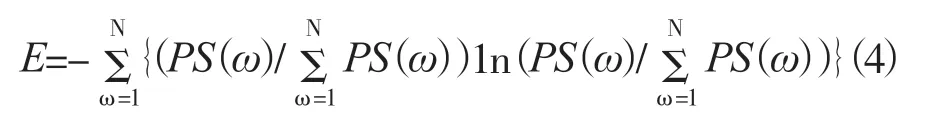
2.3 自适应神经模糊推理系统

ANFIS充分利用神经网络的数据学习能力和模糊逻辑的推理能力，其具有模糊化层、推理层、归一化层、逆模糊化层和输出层，ANFIS基本结构如图1所示[6]。

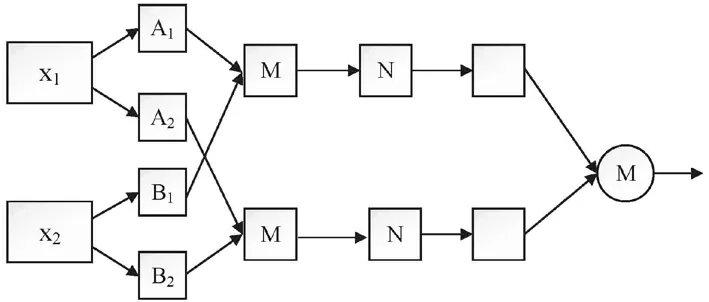
图1 ANFIS基本结构

模糊化层：实现将输入层的输入根据隶属度函数进行模糊化，该层节点的输出为：

其中x1、x2为输入，μAi、μBj为隶属度函数。

推理层：该层实现计算模糊规则的强度，该层的输出是相对应输入的隶属度的乘积：

归一化层：在该层根据以下公式计算节点的输出，具体公式为：

逆模糊化层：在该层产生模糊推理规则，该层的输出为：

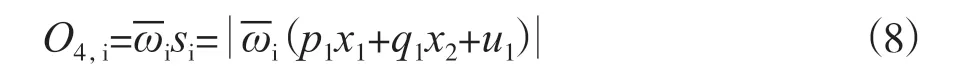
其中｛p1，q1，u1｝为该层的参数集，被称为后续参数。

输出层：该层实现整体系统输出，计算如下：

3 实验数据获取

本实验数据在国电大渡河流域大岗山水电站泄洪洞弧形工作闸门上获取，在某一特定工况下，采用成都众柴有限公司自主研发的三向加速度传感器，传感器安装在上、下支臂前端，监测闸门刚性支承的振动响应，采用16位24通道同步采集卡进行振动数据采集，采样频率为2 000 Hz。传感器测点布置图、现场安装图如图2、图3所示。

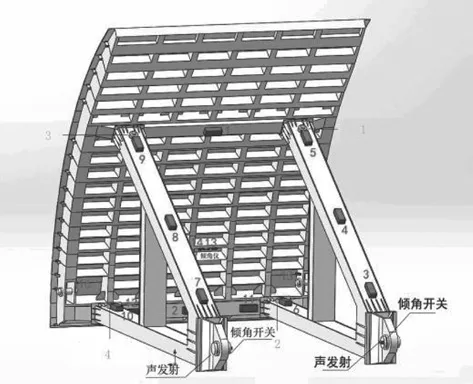
图2 传感器测点布置图

图3 现场安装图

4 算法验证及分析

在以上实验数据获取过程中，设置采集卡采样频率为2 000 Hz，每个数据样本为2 560点，所获得的水工金属闸门正常状态和异常状态的振动信号如图4所示，及其对应的频谱图如图5所示。

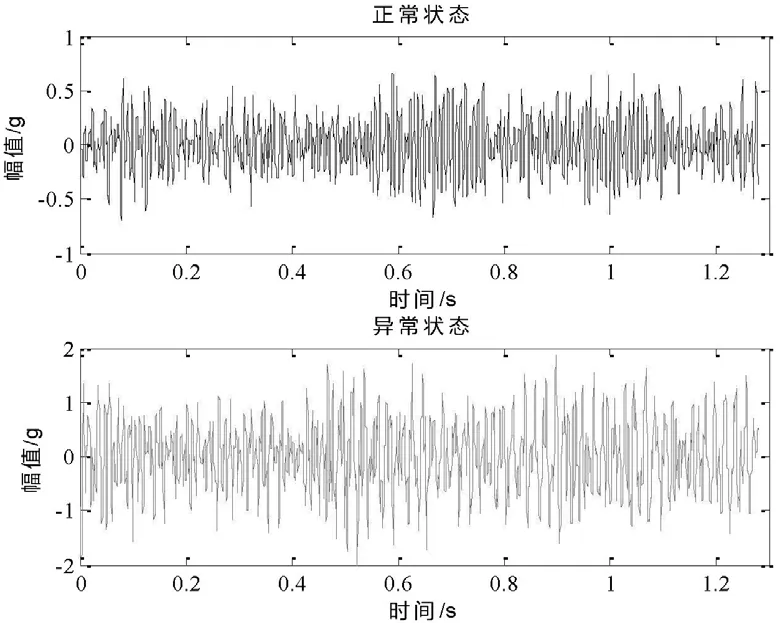
图4 正常状态和异常状态的振动信号

图5 正常状态和异常状态的频谱

从图4时域波形可知，异常状态发生时，信号时域波形幅值具有一定增大，信号频谱额外信号成分增多，但是仅属于定性分析，无法从定量角度进行异常状态判断。采用EEMD对以上振动信号进行分解，设定EEMD添加噪声次数为50，每次增加噪声幅值系数为0.15倍的信号标准差。所获得的EEMD分解结果分别如图6和图7所示。

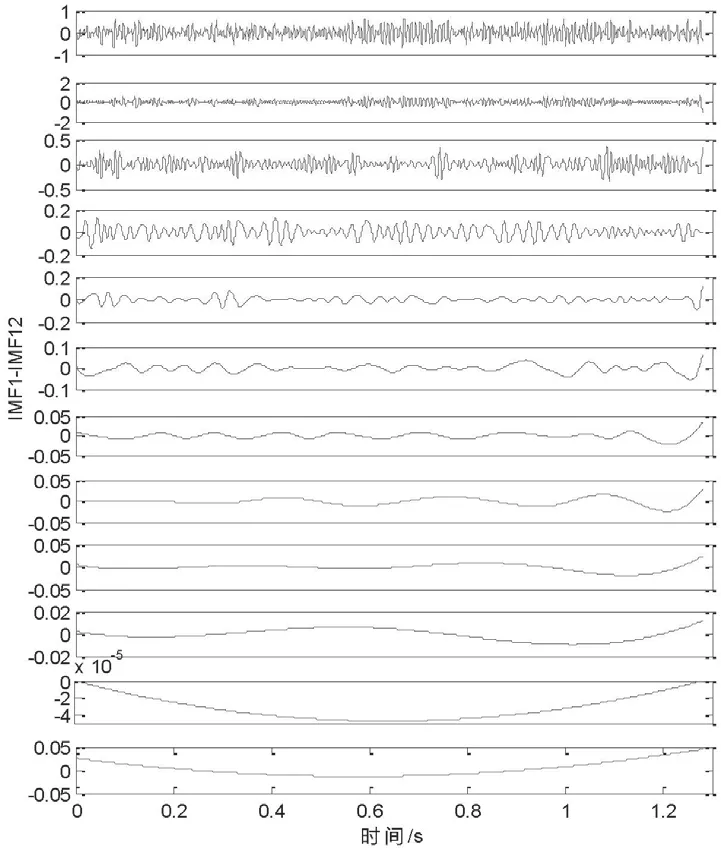
图6 正常状态EEMD分解结果

图7 异常状态EEMD分解结果

通过EEMD分解，获得12个IMF分量，将水工金属闸门振动信号中包含的状态信息按照信号特性分解到各IMF分量中，从图7、图8中可看出IMF7~IMF12主要包含趋势信息，因此选择IMF1~IMF6进行深入分析，采用功率谱熵对IMF1~IMF6进行特征量化提取。对水工金属闸门正常状态和异常状态的一系列样本提取功率谱熵特征，所获得的各IMF分量功率谱熵分布如图8所示。

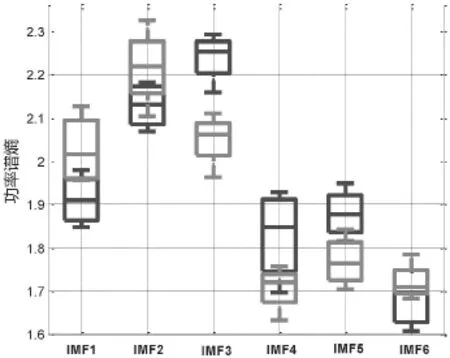
图8 正常状态和异常状态功率谱熵分布

从图8中可以看出，观察一定数量样本IMF1~IMF6的功率谱熵，可以发现，在IMF1~IMF2，异常状态的功率谱熵大于正常状态；在IMF3~IMF5，正常状态的功率谱熵大于异常状态。在IMF1~IMF2，以及IMF4~IMF6，正常状态和异常状态的功率谱熵存在一定混叠。

结合ANFIS进行状态识别。根据所提取的IMF1~IMF6的功率谱熵，ANFIS的输入为6，每个输入设定对应3个隶属度函数，分别为高、中、低；实验中区分水工金属闸门正常状态和异常状态，ANFIS输出为2，正常状态样本标记为1，异常状态样本标记为2。随机建立训练样本和测试样本，其中每种状态训练样本50个，测试样本50个。利用训练样本对ANFIS进行训练，设定均方根误差对训练过程进行控制，训练次数设置100，初始训练步长为0.01，训练完毕后，每个ANFIS输入的隶属度函数调整为最优质，所获得的每个ANFIS输入的隶属度函数如图9所示。

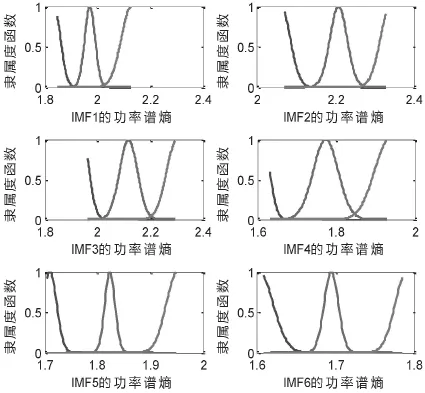
图9 训练完毕后ANFIS的隶属度函数

训练完成后，采用测试样本进行状态识别能力验证，每种状态50个测试样本，所获得的测试结果如表1所示。

表1 ANFIS状态识别结果

从表1中可以看出，正常状态识别率达到98%，平均识别率达到95%，从实验数据处理结果可看出所提出方法是一种有效的水工金属闸门状态识别方法。

5 结论

提出一种基于振动信号分析的水工金属闸门状态识别方法。利用EEMD将水工金属闸门振动信号进行分解，振动信号中包含的状态特征信息根据信号特性被分解到一系列IMFs中。结合信息熵理论，利用功率谱熵进行特征提取，证明功率谱熵能够量化水工金属闸门状态特征；最后利用ANFIS的数据学习能力和推理能力实现水工金属闸门状态识别。在某种工况的条件下进行了实验验证，证明所采用的基于振动信号分析的水工金属闸门状态识别方法具有较好效果，下一步可在更多工况条件下开展实验研究。