MRD优化布置对水电机组轴系振动控制的影响
张 宁
(中核第四研究设计工程有限公司,河北 石家庄 050021)
前言
随着越来越多的大型水电机组投入运行,由于其尺寸大、相对刚度较弱等引起的机组轴系振动问题,已成为影响大型水电机组平稳运行的关键技术问题[1,2]。目前,关于水轮发电机组振动的研究,主要以有限单元法和构建动力学模型法为主[3]。在研究机组轴系振动方面前人已取得了很多研究成果,如ZENG等、SAEEED等通过理论推导或利用数值模拟软件建立水电机组轴系振动模型[4,5]。MA等为研究水电机组自振特性和系统稳定性,提出了利用轴的摆度确定导向轴承动态特性系数的方法[6]。
近年来,人们利用磁流变阻尼装置(Magnetorheological Fluid Damper,MRD)进行结构减震,且已研制应用于多场景的减振阻尼控制器。得益于其刚度和阻尼可控性好的特点,其已应用于建筑、海洋石油平台、桥梁等结构的振动控制[7]。在实际工程中,许多半主动控制系统都采用磁流变阻尼材料,有学者提出同时考虑整体阻尼和刚度变化的结构,并进一步讨论了参数对结构刚度和阻尼变化的影响[8]。
文中基于磁流变液的水轮发电机组轴系非线性模型[9],利用最优化的方法,定义了MRD的位置函数,通过以MRD速度响应函数为中间变量,推导得出带有位置参数的MRD阻尼力模型,将其引入到水轮发电机组轴系模型中,进而建立了含有位置参数的MRD机组轴系非线性动力学模型。通过位置参数的调整实现对阻尼器的优化布置,结合MRD阻尼器不同布置位置时系统的振型特征和振幅变化,实现对机组轴系振动最优的控制效果。
1 带位置参数的MRD水电机组轴系非线性动力学模型
1.1 MRD力学模型
MRD是一种新型的减振装置,为了描述磁流变阻尼器的动态力学特性,SAKAI等在LuGre力学模型的基础上,通过推导将MRD非线性阻尼力方程写为以下形式[10]:

其中,f是阻尼力,x·是活塞速度,σ1是β(t)的阻尼系数(Ns/m),V是输入电压,β(t)是内部状态变量,σb是受V影响的粘性阻尼系数(Ns/mV),σ0是受V影响的β(t)的刚度(N/mV),σ2是粘性阻尼系数(Ns/m),σa是β(t)的刚度(N/m),a0是常数值。
1.2 水电机组轴系振动影响因素
水电机组轴系简化模型由发电机转子、上下导轴承、水轮机转轮、水导轴承以及转轴组成。磁流变阻尼器可施加于转轴上,分别布置于x、y两个方向上。简化模型如图1所示。水电机组振动实际上是作用于机组各种力之间的相互作用,因此机组轴系模型可简化为作用于机组力的模型。
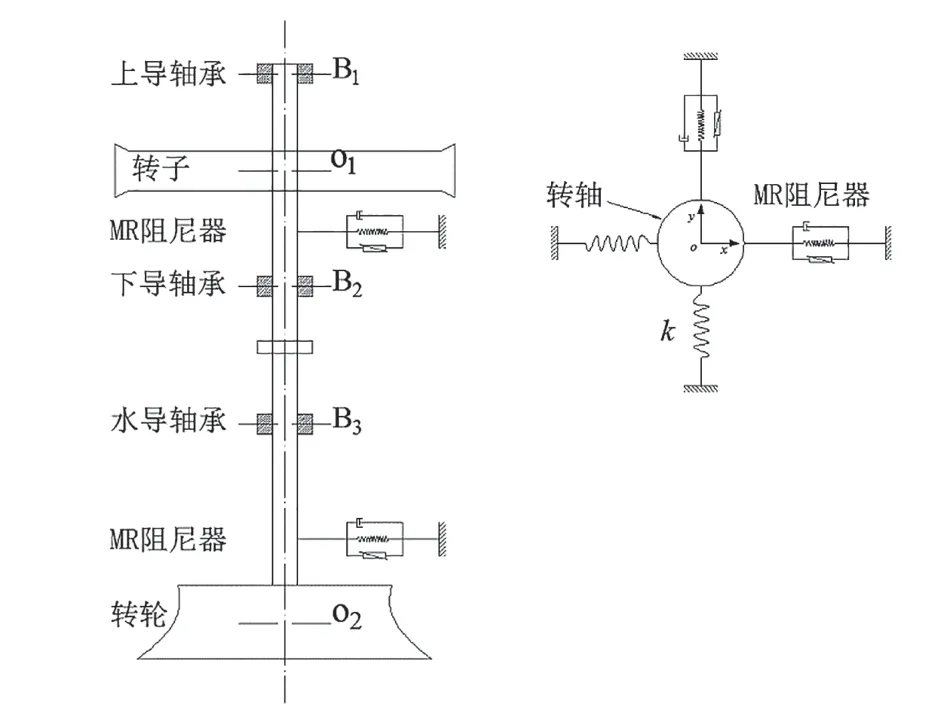
图1 水电机组轴系简化模型
1.2.1 阻尼力
水电机组稳定运行时,机组阻尼力有多种来源,如构件之间摩擦,内摩擦以及和外部介质的相互作用引起的阻尼,运行中以上因素同时存在,难以单独分离开进行分析。因此在动力学分析中采用等效粘性阻尼来将以上因素统一考虑,其阻尼力可写为以下形式[11]:
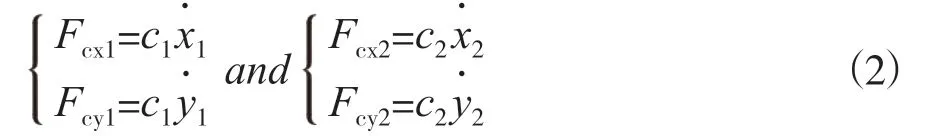
式中,c1为转子阻尼系数,c2为转轮阻尼系数。
1.2.2 不平衡磁拉力
机组运行时由于转子偏心会使转子和定子之间产生不均匀气隙,导致转子和转轮之间磁场的不均匀,进而使机组产生不平衡磁拉力。不平衡磁拉力与机组磁极对数有关,磁极对数大于3时,表达式[12]写为:
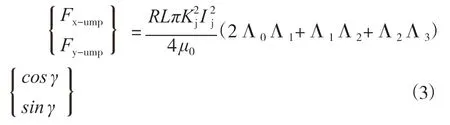
式中,Λn为气隙磁导Fourier系数;R、L分别为发电机转子半径和长度;Ij为励磁电流;Kj为气隙基波磁动势系数;γ为发电机转角。
1.2.3 非线性密封力
水轮机有多种水封形式,但不管什么形式都会使随转轮转动的水体对转轮产生激振,这时密封力呈现非线性特征,其流体动力学方程比较复杂。文献中将密封力描述为如下形式[2]:
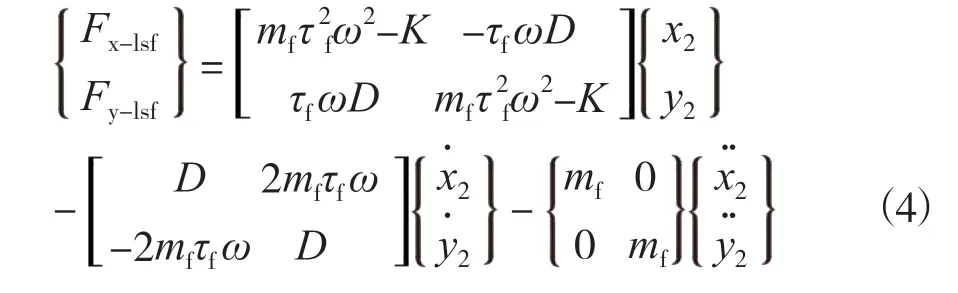
式中,mf为当量质量;D为当量阻尼;K为当量刚度;并且K、D、τf都是转轮形心扰动位移x2、y2的非线性函数。
1.2.4 非线性油膜力
通过前人的研究,我们知道Reynolds偏微分方程一般不能给出解析的积分表达式,因此要获得非线性油膜力,需要针对轴承长度边界条件,简化受力情况。Capone模型在计算时收敛性和准确性较高,采用Capone模型来计算水电机组轴系非线性油膜力[2]。其表达式为:

式中,σ为Sommerfeld修正系数,σfx-ym、σfy-ym分别为油膜力的无量纲分量。
1.3 基于MRD的水电机组轴系非线性动力学模型
文中只考虑机组轴系横向振动,忽略推力轴承的影响,机组大轴和轴承均假设为刚性。根据转子系统动能公式可推导出机组轴系总动能。
在 图1中 令|B1B2|=a、|B2B3|=b、2|B3O2|=c、|B1O1|=|O1B2|,则可以得出转子、转轮横向位移r1、r2,可设r3、r4和r5分别为转轴在上导、下导和水导轴承处的横向位移。为使计算简便可令a=b=2c,进而可得到机组系统势能。
通过将MRD非线性阻尼力引入系统广义力中,可得到系统广义力模型。综合上述式(1)、(2)、(3)、(4)、(5)得到系统广义力模型为:

通过对机组系统动能、位能计算,结合系统广义力,由拉格朗日方程推导得出水电机组轴系运动微分方程为:
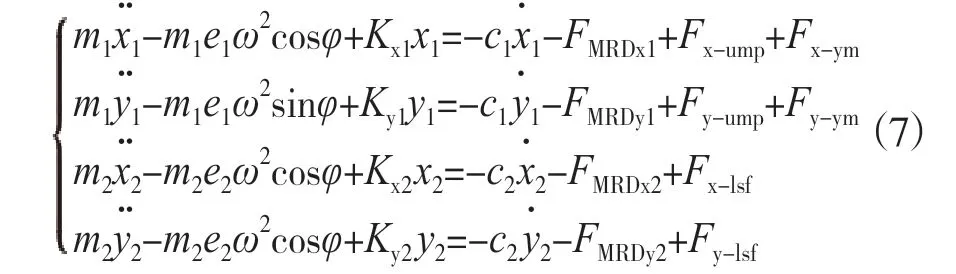
式中,Kx1、Ky1、Kx2、Ky2表达式为:
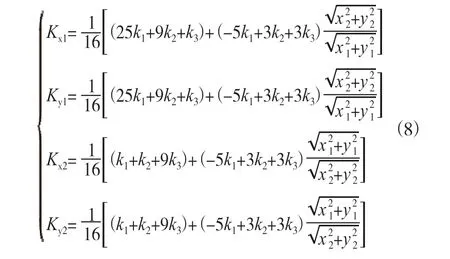
其中,k1、k2和k3分别为上导、下导以及水导轴承处的支撑刚度。
1.4 带位置参数的MRD水电机组轴系非线性动力学模型
利用最优化的方法,将位置参数引入到MRD阻尼力模型中,可通过位置参数进一步确定阻尼器的最优布置位置。最优化问题描述为[13]:
求解出变量x1,x2,…,xn的值,使评价函数f(x1,x2,…,xn)达到最大值或最小值,这就是最优化问题。针对MRD阻尼器布置位置问题,显然决策变量为布置位置,评价函数为机组动力学微分方程。
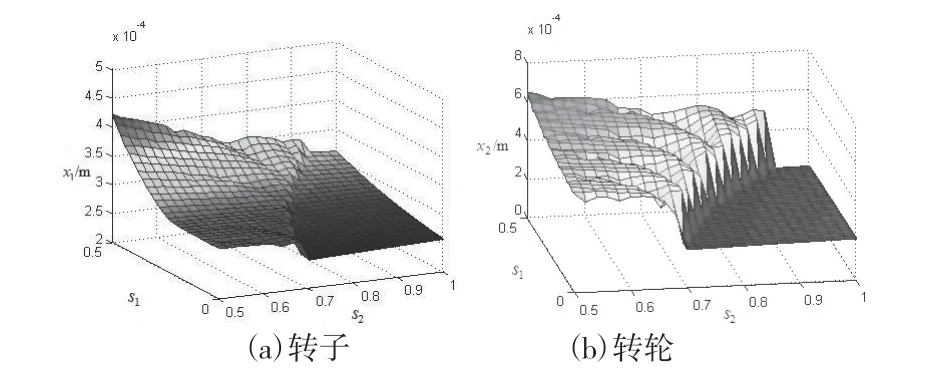
因此为表示MRD阻尼器在水轮发电机组轴系中的具体布置位置,我们定义s1、s2(0 其中L=|B1B2|+|B2B3|+|B3O2|为机组大轴总长度,s1、s2在(0,1)之间取值可保证MRD阻尼器取到大轴上任意位置。 由前文可知转轴假设为刚性,将阻尼器位置函数引入转子、转轮径向位移函数公式,得到阻尼器径向振动位移函数,对其求导可得到MRD阻尼器径向振动速度与转子、转轮轴系振动速度的函数关系为: 基于已知的MRD阻尼器阻尼力模型,将推导的含有位置参数的阻尼器振动位移函数和速度函数带入阻尼力模型中,可得到含有位置参数的MRD阻尼力模型: 为简化方程减小运算量,仍采用1.3中的假设,即a=b=2c。则得到带位置参数系统状态方程为: 算例采用南方某水电站机组物理参数,算例数值计算时所采的MRD阻尼器无量纲参数值如表1所示,该MRD模型参数相对于输入电压具有双线性形式,由于摩擦模型的特性,所有参数均取为正值,粘性阻尼系数与输入电压成正比。 表1 MRD所采用参数值 在引入位置参数后,以位置参数为自变量,通过位置参数的变化探究阻尼器布置位置对水电机组减振效果的影响,由于位置参数s1位于取值处于上导轴承和下导轴承之间,轴承对大轴约束强,参数变化对机组振型影响较小。因此着重对位置参数s2的变化时的机组振型进行分析,将位置参数s1设为定值,分析位置参数s2与机组振动的关系。如图2所示为机组振动状态关于位置参数s2的分岔图。从图2中可以看出,在s2变化时机组存在明显的周期和拟周期运动,并且机组振幅在10-4量级,说明拟周期性较强。当s2>0.76时,机组振动为稳定的周期态,且明显抑制了机组额外谐波分量。 图2 以s2为控制参数转子、转轮分岔图 通过上述分析根据机组运动形式大致确定了s1、s2的取值范围,以下结合机组振动幅值的变化进一步确定阻尼器的最优布置位置。如图3所示为转子、转轮振动最大幅值关于位置参数s1、s2的曲面图。从图3中曲面上可以明显看出不论转子还是转轮,曲面上都有一个类似“断崖式”的振幅突降,这些振幅突降坐标在位置参数s1、s2平面上构成了一条曲线,暂且称该曲线为“振形线”,这条曲线两侧位置参数分别对应系统不同运动形式。由于位置参数越过该曲线之后,转轮响应由拟周期运动变为周期运动,因此振动幅值趋于平稳。这也是转轮在该曲线附近出现明显“断崖式”位移突降的原因,并且从图3(b)中可以看出位移突降后转轮位移稳定在0.215 mm左右,位置参数变化对转轮振幅影响也响应减小。 图3(a)中转子振幅变化情况则与转轮不同,从图3(a)中看出在位置参数越过“振形线”后,系统参数变化对其振幅仍有影响。其振幅随着s1的减小、s2的增加而减小,即在上阻尼器向转子靠近,下阻尼器向转轮靠近这个过程中,转子振幅是在不断减小的。 图3 转子、转轮不同位置参数下三维振幅曲面图 文章通过将位置参数引入到MRD水电机组轴系非线性模型中,建立了含有位置参数的MRD机组轴系非线性动力学模型,研究了不同阻尼器布置位置对机组的减振控制效果。研究结果表明,不同阻尼器布置位置对机组振动形式和振幅控制有明显的影响,整体来说,阻尼器布置位置对转子的影响要小于对转轮的影响,通过调整位置参数使其位于机组系统“振形线”右侧,可以使转子、转轮都保持周期运动稳定状态,有效抑制机组系统振动的额外谐波分量、减小机组振动幅值。
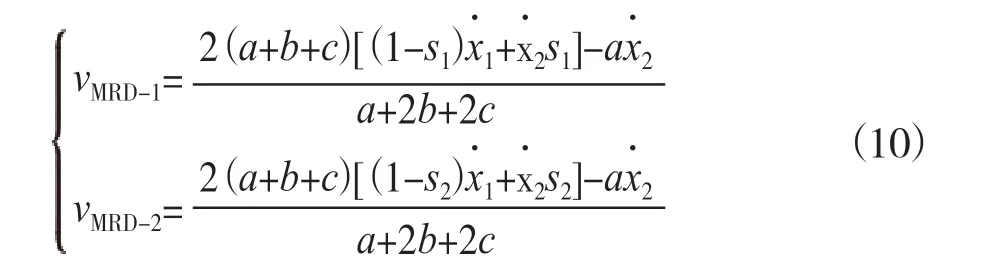
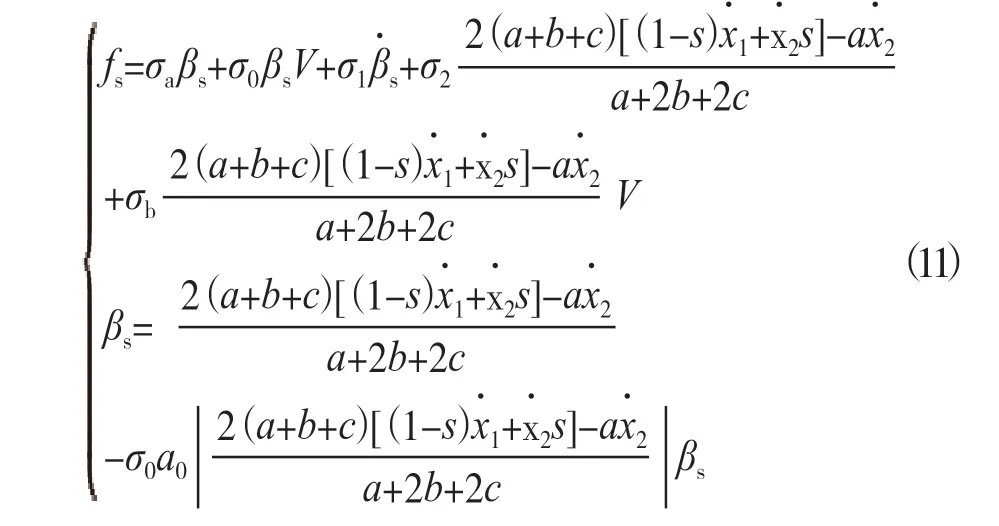


2 不同MRD阻尼器布置位置情况下水电机组减振效果分析
2.1 基于振型分析

2.2 基于振幅分析
3 结论
——“AABC”和“无X无X”式词语

