混流式水轮机轴向水推力随工况和含沙水参数的变化

赵 炜，邹晓阳，闵占奎，王文欢，王颢钧

（1.国网甘肃省电力公司电力科学研究院，甘肃 兰州 730070；2.上海电力大学能源与机械工程学院，上海 201306；3.国网甘肃综合能源服务有限公司，甘肃 兰州 730070）

0 引言

水电是可再生清洁能源，生产成本大幅低于煤电，因此发展水电不仅有助于环保、减少碳排放，而且能够减少对煤炭等不可再生资源的消耗。我国水力资源丰富，主要位于西部地区，如黄河、长江、金沙江等，水电开发潜力巨大。然而部分河流泥沙含量大，容易导致推力轴瓦烧损和事故停机，造成很大经济损失。2018年7月，刘家峡水电厂新投运的7、8号机组——两台位于“穿黄排沙”洞出口处的水轮发电机组带额定负荷运行，短时间内推力轴承温度迅速上升超过报警和停机温度，造成推力轴承烧损事故[1]。推力轴承烧损的主要原因之一是轴向水推力大，导致弹性塑料推力瓦面油膜减少或消失，推力瓦面发生干摩擦，温度急剧升高，超出推力瓦温度上限[1]。此外，白岩水电站、龙羊峡水电站和尼泊尔崔树里水电站的推力轴承烧瓦事故，也均由轴向水推力过大引起[2]。

近几年，王伟 等通过模型试验和现场测试的方法研究了水推力，分析了水推力过大的原因[3]。CFD仿真技术具有工作量小、时间短、成本低、参数化分析方便等优点，已经广泛应用于流体流动模拟与分析。唐聪 等基于ANSYS CFX仿真分析了古里水电站混流式水轮机真机和模型上冠流域在不同泄水减压结构下的流动状况、相对泄漏量和轴向水推力[4]。李浩亮 等利用CFD计算了混流式蓄能机组的轴向水推力，并与现场测试的结果进行比较，得到了轴向水推力随出力和水头的变化规律[5]。JI 等人提出水轮机主流道CFD仿真结合上冠和下环理论计算的方法来计算水轮机轴向水推力，分析了轴向水推力随水头和流量的变化，与实验测试结果相符[6]。基于CFD多相流对混流式水轮机含沙水流动进行仿真的研究工作也开展了不少。黄剑峰 等、廖姣 等和孙毅 等利用ANSYS FLUENT模拟了泥沙密度、泥沙直径、泥沙浓度3个参数中的1个或几个变化时含沙水在水轮机主流道内的稳态流动状况，分析了泥沙对水轮机的磨损情况[7-9]。然而，水轮机全流道轴向水推力随工况参数和含沙水参数的变化还有待进一步研究。

文中针对刘家峡水电厂的新投机组[1]，分别建立水轮机主流道、上冠流道和下环流道的CFD仿真模型，采用MIXTURE多相流模型和RNG k-ε两方程模型模拟含沙水固液两相流，基于FLUENT求取各流道的稳态流场，通过流道合成计算获得水轮机全流道的轴向水推力，分析其随工况参数和含沙水参数的变化。

1 混流式水轮机含沙水流动仿真模型

1.1 混流式水轮机全流道模型及边界条件

根据混流式水轮机轴向水推力的研究文献[2],轴向水推力F包含3个主要分力，分别为流体作用在转轮内表面的轴向分力F1、作用在上冠外表面的轴向分力F2和作用在下环外表面的轴向分力F3，即：

其中，转轮内表面包括叶片外表面、上冠内表面和下环内表面。通过建立混流式水轮机的主流道、上冠流道和下环流道的模型进行仿真计算，合成为水轮机全流道的轴向水推力。

参考刘家峡水电厂的新投机组[1]，建立水轮机主流道、上冠流道和下环流道的三维几何模型，如图1所示。主流道比较复杂，沿流动方向依次为蜗壳、固定导叶、活动导叶、转轮和尾水管，轮廓尺寸约为长33 m、宽17 m、高17 m，转轮最大外径约为5 m，流道入口直径约为6 m，出口为尾水管出口。上冠流道的入口为宽度很窄的圆环面，无减压泄水口，不考虑微小泄漏，上冠流道无出口。下环流道的入口为宽度很窄的圆环面，出口为高度很小的圆柱面。

利用ICEM CFD对水轮机流道进行网格划分，流道内部划分为六面体网格，流道表面划分为四边形网格，对近壁面网格进行加密。通过interface将蜗壳、固定导叶、活动导叶、转轮、尾水管的网格组装起来，获得主流道网格，如图2所示。主流道网格总数约为710.3万，其中转轮网格数约为204万。转轮的叶片数为15，根据转轮的旋转周期结构，上冠流道和下环流道均在周向上取整体的1/15进行网格划分，以减小网格模型。上冠流道网格数约为17.4万，下环流道网格数约为31.5万。

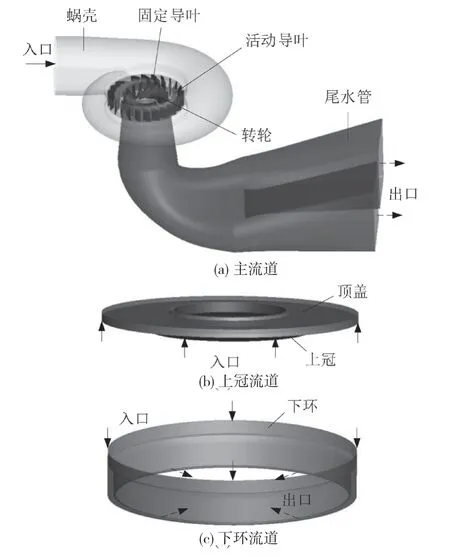
图1 水轮机全流道三维模型

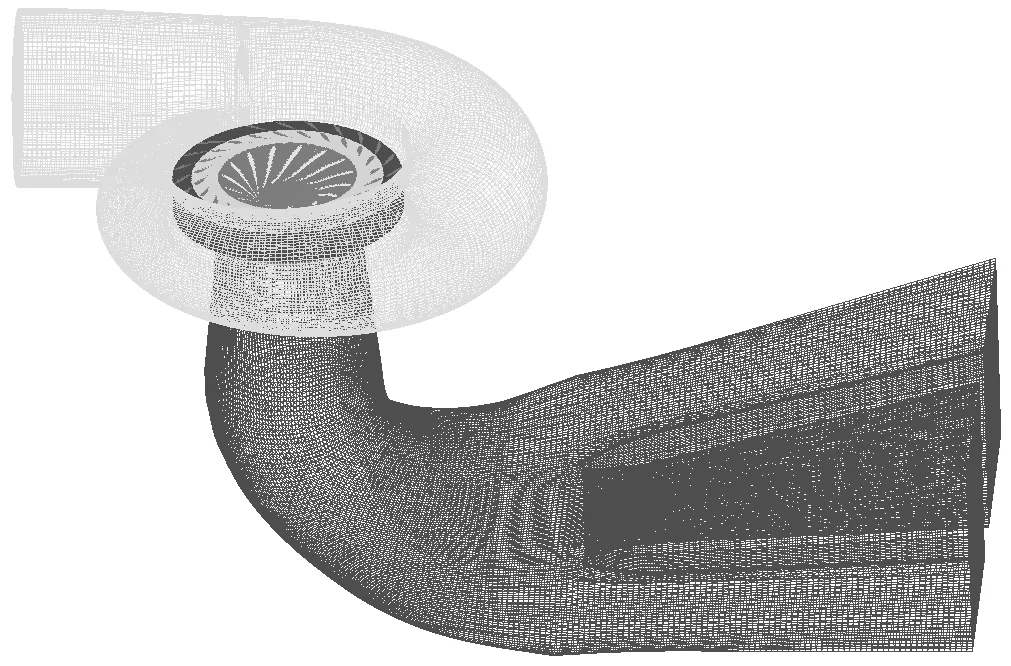
图2 主流道网格

主流道入口采用速度入口边界条件，在湍流流动下，速度分布采用纯经验幂律公式描述，入口压力将水头和平均流速代入伯努利方程计算得出。主流道出口为压力出口，出口压力设为0。采用冻结转子方法来模拟转轮流域与其前后的静止流域的界面作用，转轮壁面跟随转轮流域一起转动，其余壁面静止，壁面与流域之间无滑移。上冠流道和下环流道入口均为压力入口，入口压力设置为主流道稳态流动时相应位置的平均压力。下环出口为压力出口，出口压力设为0。

1.2 含沙水流动控制方程和求解

含沙水属于固液两相流，主相为水，次相为泥沙。文中主要关注含沙水对水轮机轴向水推力的影响，基于ANSYS FLUENT 2019平台对含沙水流动进行仿真时，选择MIXTURE多相流模型。MIXTURE多相流模型属于欧拉-欧拉方法，将固体颗粒视为与连续相相互渗透的拟流体进行处理，计算量适中，计算稳定性好，工程应用广泛。

MIXTURE模型的连续性方程、动量方程、次相的体积分数方程分别为

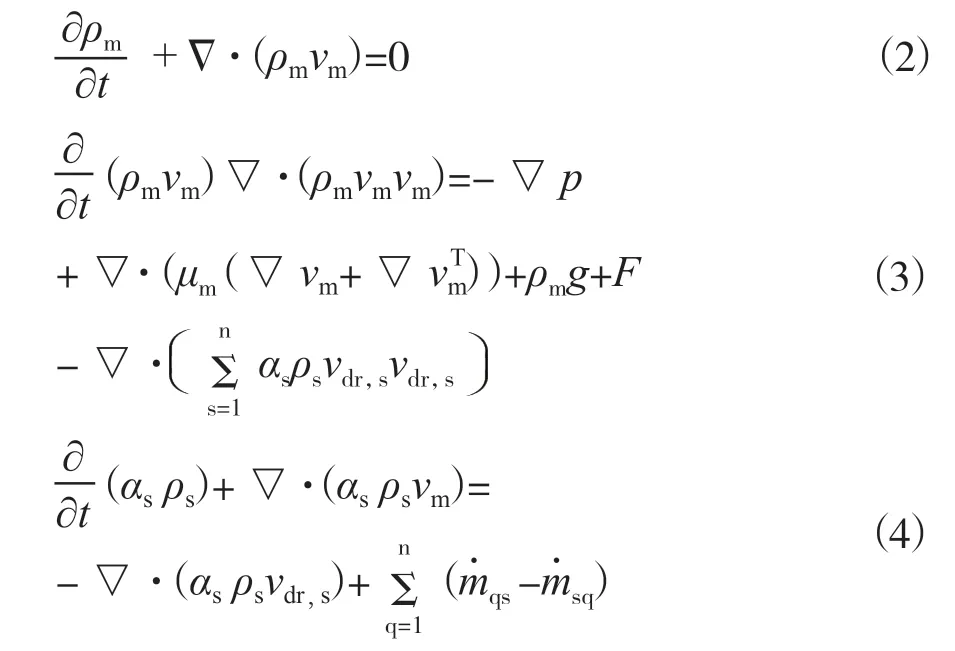
其中t为时间，ρm是含沙水的平均密度，vm是质量平均的速度矢量，p为压强，g为重力加速度向量，F为体积力向量，μm为体积平均的动力粘度，n为多相流的相数，αs为第s相的体积分数，vdr,s为次相s的漂移速度向量，次相体积分数方程等号右边第二项求和项为相间质量转化速率[10]，▽为向量微分算子。MIXTURE模型利用代数滑移方程计算次相相对于主相的滑移速度，进而由滑移速度计算次相的漂移速度[10]。在ANSYS FLUENT平台上仿真时泥沙的动力粘度设置为微小量，相间的拖曳力采用Schiller-Naumann模型，相间滑移速度采用Manninen-et-al模型。

利用雷诺时均方法（Reynolds-averaged Navier-Stokes, RANS）求解含沙水固液两相流的控制方程。雷诺时均方法将瞬时速度和瞬时压力等效为短时间内的平均值与脉动值之和，代入到湍流流动控制方程中，因湍流脉动出现的新应力项，称为雷诺应力。目前工程上应用最广泛的湍流模型为两方程模型，即将雷诺应力表示为湍动粘度的函数，湍动粘度通过湍动能k和湍动耗散率ε的方程求解。标准k-ε模型适用于计算充分发展的湍流，计算稳定性好，对计算资源要求不高，适合于较大雷诺数、低旋和弱浮力的湍流模拟。RNG k-ε模型与标准k-ε模型相似，对标准k-ε模型进行了修正，除了适合于较大雷诺数、低旋和弱浮力的湍流模拟，也能够模拟高应变率、大曲率和低雷诺数湍流[10]。在FLUENT 2019平台上采用RNG k-ε两方程模型和标准壁面函数对含沙水流动进行模拟，模型参数值采用FLUENT中的默认值。

求解含沙水两相流的控制方程时，采用压力-速度耦合算法。压力离散采用体积力加权法，动量离散采用二阶迎风格式，体积分数、湍动能和耗散率离散均采用QUICK法。松弛因子采用比FLUENT的默认值小的值，以保证数值求解时具有良好的收敛性。

2 轴向水推力的仿真结果

2.1 额定工况下转轮内外流道的壁面压力

对额定工况下水轮机全流道含沙水流动进行稳态仿真。额定工况参数为：水头93.6 m，流量175.4 m3/s，转速136.4 r/min。含沙水参数为：水密度1 000 kg/m3，泥沙密度2 710 kg/m3，泥沙颗粒Φ 0.1 mm[11，12]。

图3和图4分别为额定工况下清水（泥沙含量0）和泥沙含量30 kg/m3的含沙水流动时转轮、上冠和下环流道壁面压力。可以看到，转轮壁面压力呈圆周对称分布，高压区位于叶片的入流区域，低压区位于叶片的出流区域及靠近出流边的背压面。叶片的工作面和背压面有一定的压力差，叶片表面的静压大体上顺着流线方向递减。上冠流域的压力较大，压力随着半径增大而增大，压力梯度也增大。下环流域最大压力位于入口处，且沿着间隙流道，压力呈均匀下降趋势。进入下环空腔，流通截面大，压力由正变负。下环底部外侧直角处出现了漩涡，流动较为复杂。泥沙含量30 kg/m3的含沙水流动时的压力分布状况与清水流动时的基本相同，转轮壁面和上冠壁面的压力略微增加，而下环壁面压力略微下降。额定工况下，清水稳态流动时的水轮机轴向水推力为9 425.8 kN，方向向下。而30 kg/m3的含沙水流动时的轴向水推力清水时的轴向水推力之比约为1.006。

2.2 轴向水推力随工况参数的变化

以额定工况下清水稳态流动时的水轮机轴向水推力为比较基准，定义轴向力比，分析轴向水推力随转速、流量、水头等工况参数的变化。仿真时含沙水参数保持不变。

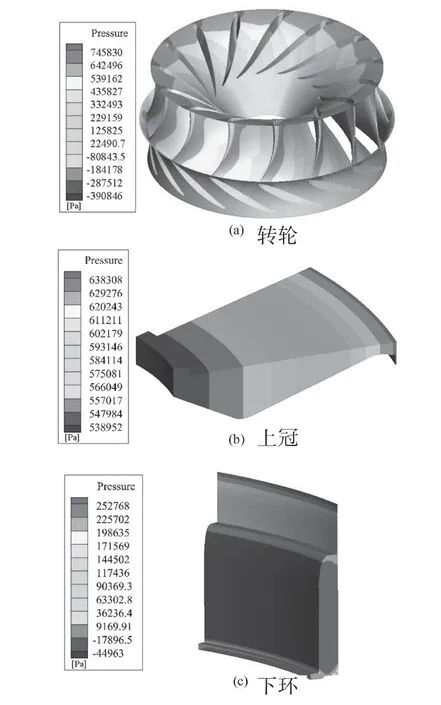
图3 额定工况清水流动水轮机流道壁面压力

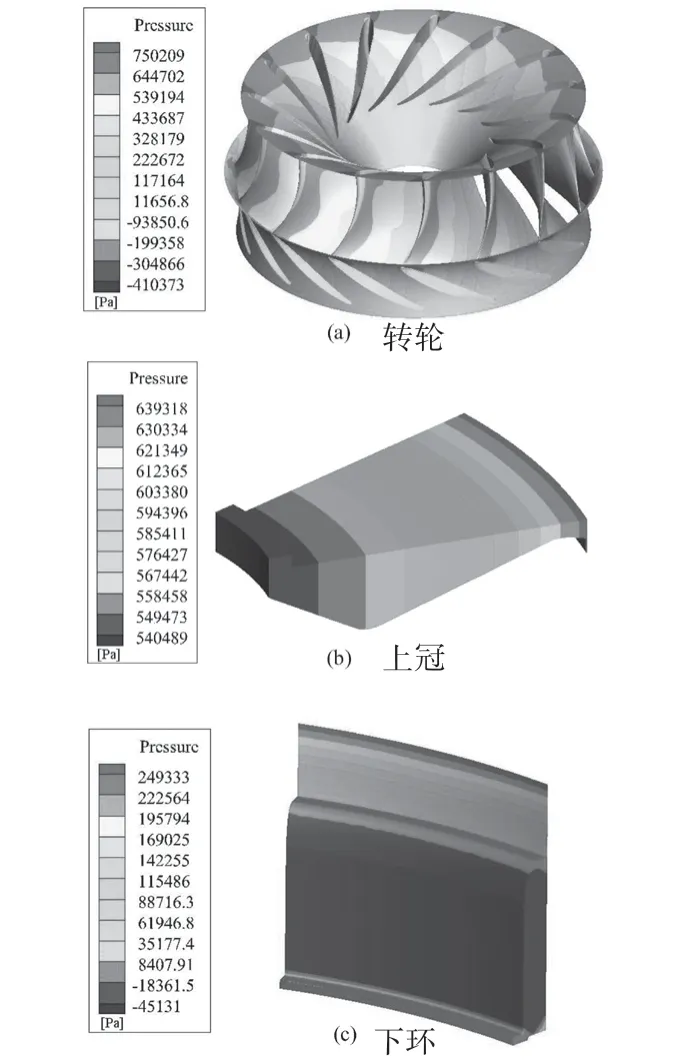
图4 额定工况泥沙含量30 kg/m3的含沙水流动水轮机流道壁面压力

图5 为水头为93.6 m时不同转速下水轮机轴向水推力比随流量的变化曲线，图6为流量175.4 m3/s时不同转速下水轮机轴向水推力比随水头的变化曲线。可以看到，含沙水参数不变时，在0.85~1.15倍的额定转速范围内，转速对水轮机轴向水推力的影响不大，除了流量95.4 m3/s处轴向力比值的最大差值约为10%之外，其他流量下轴向力比值的最大差值在5%以内，图6很清楚地表明了这一点。水头对轴向水推力的影响更小，图6所示流量175.4 m3/s时相同转速不同水头下轴向力比值之差在1%以内。流量对轴向水推力的影响最大，如图5所示，流量从95.4 m3/s增加到175.4 m3/s时，轴向力比值从约0.3近似线性增加到1.0左右。

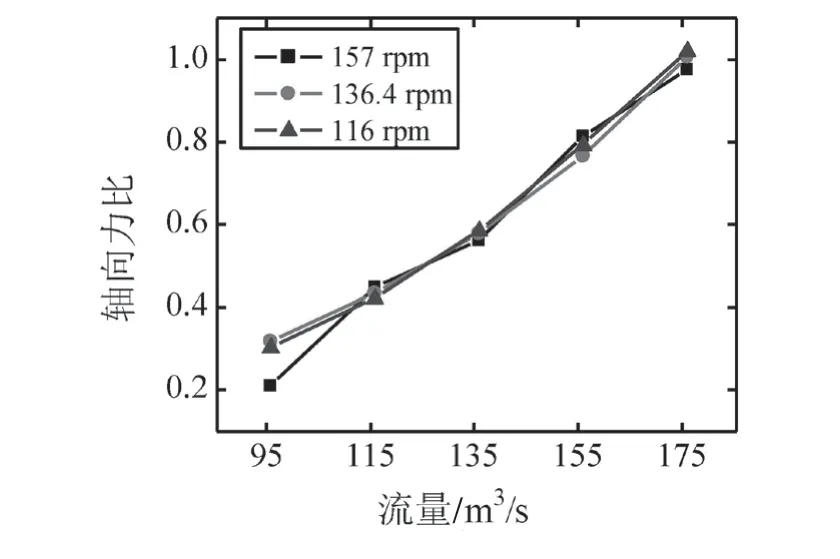
图5 不同转速下水轮机轴向水推力比随流量的变化

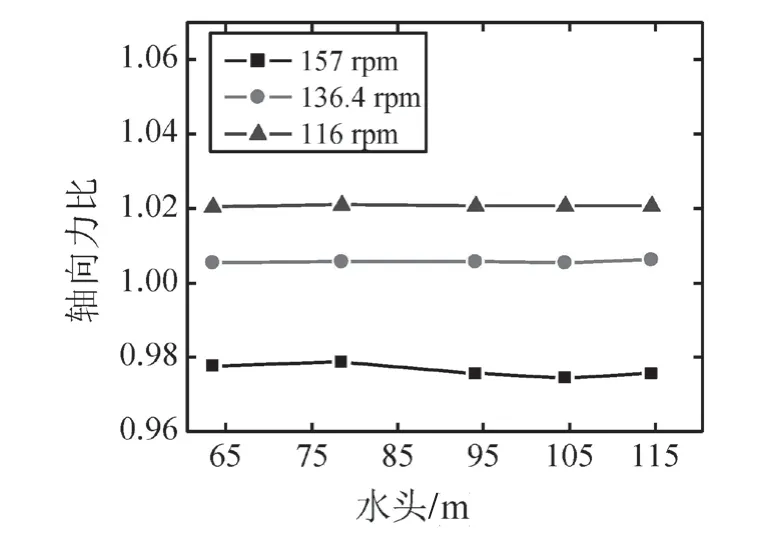
图6 不同转速下水轮机轴向水推力比随水头的变化

2.3 轴向水推力随含沙水参数的变化

保持工况参数与额定工况参数相同，仿真分析轴向水推力随泥沙密度、泥沙直径、泥沙含量等含沙水参数的变化。

图7为泥沙含量30 kg/m3时不同泥沙密度下水轮机轴向水推力比随泥沙颗粒直径的变化曲线，图8为泥沙颗粒直径0.1 mm时不同泥沙密度下水轮机轴向水推力比随泥沙含量的变化曲线。可以看到，泥沙含量很小（如30 kg/m3）时，泥沙密度在1 710~2 710 kg/m3的范围内变化时，对水轮机轴向水推力的影响较小。泥沙颗粒直径对轴向水推力的影响也很小，图7所示泥沙含量30 kg/m3时相同泥沙密度不同颗粒直径的轴向力比之差在1%以内。其他参数保持不变时，轴向水推力增大随泥沙密度的增大而增大。泥沙含量越大，不同泥沙密度下的水推力比值相差越大，如图8中泥沙含量为210 kg/m3时，2 710 kg/m3密度下的轴向水推力比与1 710 kg/m3密度下的增大5%。泥沙含量对轴向水推力的影响很大。泥沙含量从30 kg/m3增加到210 kg/m3时，轴向力比值近似线性增加，且密度越大，增加的幅度越大，密度为1 710 kg/m3时增加约7%，密度为2 710 kg/m3时增加约12%。

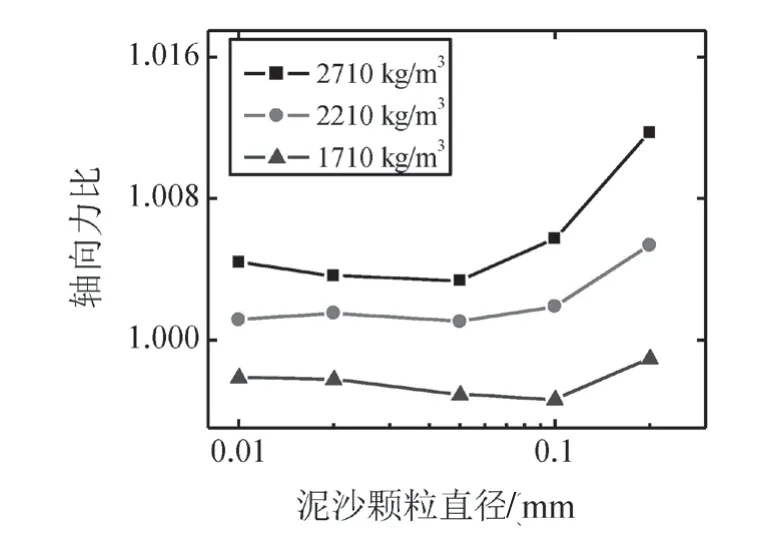
图7 不同泥沙密度下水轮机轴向水推力比随泥沙颗粒直径的变化

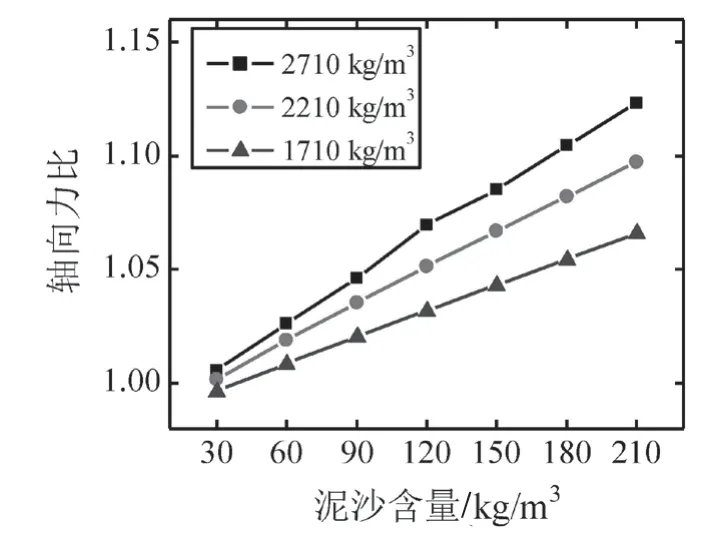
图8 不同泥沙密度下水轮机轴向水推力比随泥沙含量的变化

根据上述的仿真结果和分析，可以看到含沙水在水轮机中流动时，对水轮机的轴向水推力会产生较为复杂的影响。与清水相比，含沙水增大了水轮机轴向水推力，尤其在泥沙含量很大时，将会大幅度地增加轴向水推力，这是造成过流泥沙含量大的水轮发电机组推力轴瓦烧损的原因。在工况参数中，流量对轴向水推力的影响最为显著，减小流量可以明显地减小水推力。文中的研究对于减小混流式水轮机轴向水推力以避免推力轴瓦烧损具有重要的指导意义。含沙水在水轮机中的流动及其引起推力轴瓦烧损是非常复杂的，今后将考虑CFD瞬态仿真分析和试验测试等深入研究水轮机的轴向水推力。

3 结论

文中建立水轮机主流道、上冠流道和下环流道的CFD仿真模型，在ANSYS FLUNET中采用MIXTURE多相流模型和RNG k-ε两方程模型对水轮机含沙水的湍流流动进行稳态计算，获得了水轮机全流道的稳态流场，分析了水轮机全流道水推力随工况参数和含沙水参数的变化，获得的主要结果如下：

（1）额定工况下，清水流动和小泥沙含量（如30 kg/m3）的含沙水流动下的水轮机转轮内外流道壁面的压力大小和分布接近，含沙水造成水轮机轴向水推力增大。

（2）含沙水参数不变时，转速在额定转速附近变化或水头在上下限范围内变化时，水轮机轴向水推力的变化很小。流量从95.4~175.4 m3/s时，轴向水推力比值从约0.3近似线性增加到1.0左右。

（3）工况参数不变时，泥沙颗粒直径在0.01~0.2 mm范围内变化时，轴向水推力变化很小。泥沙密度增大时，轴向水推力增大，且泥沙含量越大，增大幅度越大。泥沙含量从30~210 kg/m3时，轴向水推力近似线性增加，泥沙密度为1 710 kg/m3时增加约7%，泥沙密度为2 710 kg/m3时增加约12%。