可变速抽水蓄能电机振动和噪声优化分析

王 博，张金仙，胡金明，王业庭，冯东磊

（1.河北丰宁抽水蓄能有限公司，河北 丰宁068350；2.国网新源控股有限公司，北京 100052；3.哈尔滨电机厂有限责任公司大电机研究所，黑龙江 哈尔滨 150000；4.国网新源建设有限公司，北京 100053）

0 引言

目前，我国可再生能源发电并网容量不断增加，间歇性、随机性的特点对电网的调峰和调频的能力提出了更为严格的要求[1，2]。抽水蓄能电站可以有效调整电网的峰值、谷值、频率、相序等，解决新能源对电网的影响。传统的抽水蓄能电站多采用同步电机，运行于同步转速，水泵水轮机处于偏离水轮机工况和水泵工况的最优效率点运行，造成水泵水轮机的振动、空蚀、泥沙磨损、以及运行效率等问题[3~5]。

电机的振动噪声不仅会对人产生干扰，同时长时间运行也会对机组造成损坏。噪声已经作为衡量电机性能的一项重要指标，涉及多学科交叉研究，主要包括电磁学、电机学、机械、声学等。电机的谐波会产生麦克斯韦径向力波，即气隙圆周以某种空间波形分布并旋转的一系列行波，在运行时径向力波随时间和空间都是交变的，从而引起电磁振动噪声。径向力波是振动噪声的主要激振源，也是研究电磁振动噪声分析的关键。苏联舒波夫最早推导出了计算电机电磁力的解析式，20世纪80年代，英国的S.J.Yang博士通过分析电动机的定子径向力频率，对振动形式进行了数学描述，对电磁力进行了进一步的理论推导和验证[6]。国内陈永校等在电机径向力波和槽配合等方面进行了深入研究。其中，磁势乘磁导法被广泛采用，但是这种方法无法计算得出准确的气隙磁密值[7]。法国Y.Lefevre提出用有限差分法计算永磁同步电机定子的电磁力[8]。芬兰A.Belahhcen用有限元法对永磁同步发电机电磁力进行了计算[9]。韩国Tac-Jong Kim应用能量的方法研究了电磁力、电磁场和机械振动的产生机理[10]。日本Takashi Kobayashi利用A-Φ法作为理论基础，先利用有限元计算气隙磁密，再代入麦克斯韦应力方程[11]。文献[12]以1台额定功率35 kW的新能源车用PMSM为研究对象，提出一种转子外缘开辅助槽的优化方案以降低电机的振动噪声，通过对辅助槽的多个参数进行多变量寻优确定最优的参数值。文献[13]对高速永磁同步电机的电磁力波和结构模态进行了分析，并分别分析电机的气隙长度、极弧系数及槽口宽度对电机振动噪声的影响。文献[14]采用粒子群算法对永磁同步电机的结构参数进行多目标优化设计，降低了气隙电磁力谐波对转矩脉动幅值影响较大的次谐波,从而实现抑制电机齿槽转矩的目标。文献[15]对低频振动的机理进行分析，低频电磁力的大小随气隙偏差、不圆度、气隙磁密增加而增大,随气隙长度增加而减小。文献[16]应用Maxwell应力方程推导出电动汽车用永磁同步电机径向电磁力的解析表达式，并在此基础上分析总结了永磁同步电机各径向电磁力的来源及阶次和频率，进一步优化了转子结构。文献[17]提出一种基于多物理场耦合的感应电机噪声分析和研究方法。将感应电机的电磁力通过谐响应分析与振动和噪声耦合起来进行计算。

1 径向电磁力分析

发电机定子铁心的振动主要是由交变的径向电磁力所引起。如图8所示,若定子上有N极、转子上为S极,气隙磁密为Bδ。根据麦克斯韦应力张量法，则得出气隙单位面积的径向电磁力Fr为

式中：μ0为真空磁导率。

若图1中N、S极在空间固定不动，Bδ不变，则Fr为一常值，不会产生振动。若气隙磁场为一旋转磁场或脉动磁场，则定子表面所受到的径向电磁力Fr将随时间而变化，导致定子铁心振动。

设电机的气隙内只有1个行波磁场bm，则气隙内1个行波磁场所产生的径向力波如下式所示。

式中：τ1为二极波的极距，τ1=pτ，ωm为从定子上观测时行波磁场的交变角频率，x为行波的位置。

根据(2)式可知,由bm所产生的径向电磁力应为：

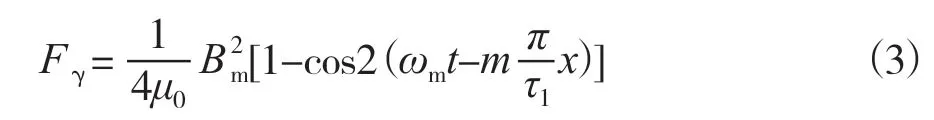
上式中第1项为常值项，不会引起振动，第2项是随时间（t）和空间（x）变化的电磁力，会引起振动，其力波的空间次数为2 m次，交变频率为2ωm。

在电机中，气隙中通常有2个行波磁场，导致径向力波的产生，其中1个为转子边的磁场，即主级磁场bm，另1个为定子边的磁场，即电枢反应磁场bn。m、n既可以是正值，也可以是负值，正值代表正向旋转行波，负值代表反应旋转行波，进一步可以推导出，电机中径向电磁力为：

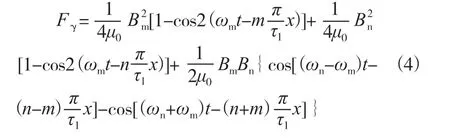
上式由3个分量组成，前2个分量是行波磁场bm、bn自身作用产生的力波，第3个分量式bm、bn相互作用产生的力波。分析第3个分量可知，其中第1项产生的空间力波的频率为fn-fm，空间次数为p′=n-m，另1个力波的频率为fn+fm，空间次数为n+m。

力波的空间次数p′不同时，会导致不同的振型，如图2所示。由于定子铁心径向电磁振动的幅值如下式所示，从式中可知，随着力波空间次数的增加，振动的幅值会大幅下降，因此，在分析定子铁心振动时，应着重考虑电枢反应磁场中反转且次数与主极磁场接近的磁势谐波。

式中：λ为振动幅值，A为振动系数，与电机结构尺寸相关。

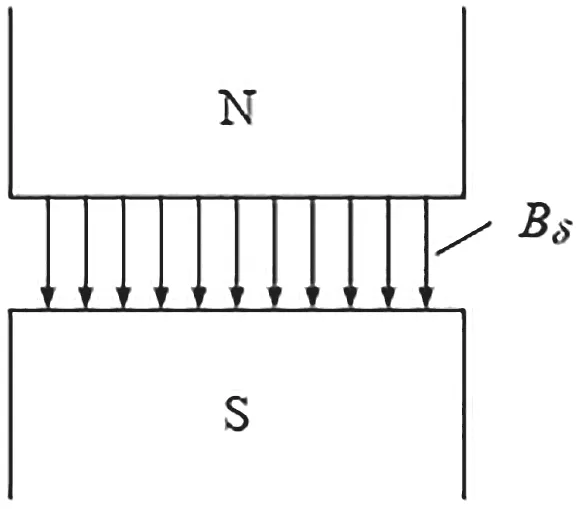
图1 定转子N、S极示意图

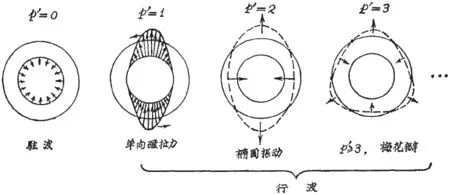
图2 定子振型

2 径向电磁力有限元分析

样机主要参数如表1所示。

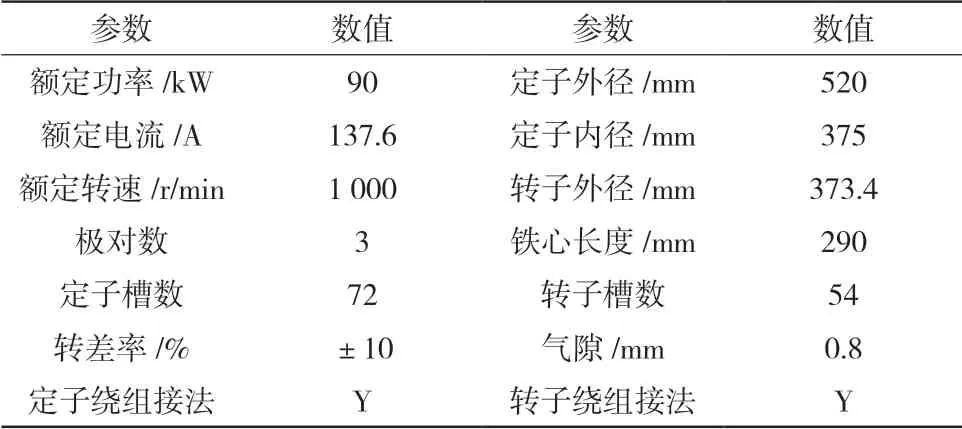
表1 样机主要参数

2.1 径向电磁力计算

可变速发电电动机的主极磁场中除基波外，还含有高次谐波。同样地，电枢磁势会产生基波和高次谐波磁场。主极磁场的基波及其谐波与电枢磁势相应的基波和谐波磁场相互作用，将产生不同频率和力波数的激振电磁力。根据上述理论分析，由式（5）可知，其振动的大小大致与激振力力波数的4次方成反比，故此处只考虑力波数较低的情况，可以计算本台可变速电机定子铁心所受的径向电磁力如表2所列，其主极磁场分布和电枢反应磁场分布如图3所示，主极磁场和电枢反应磁场气隙磁密分布如图4所示。

图3 磁场分布

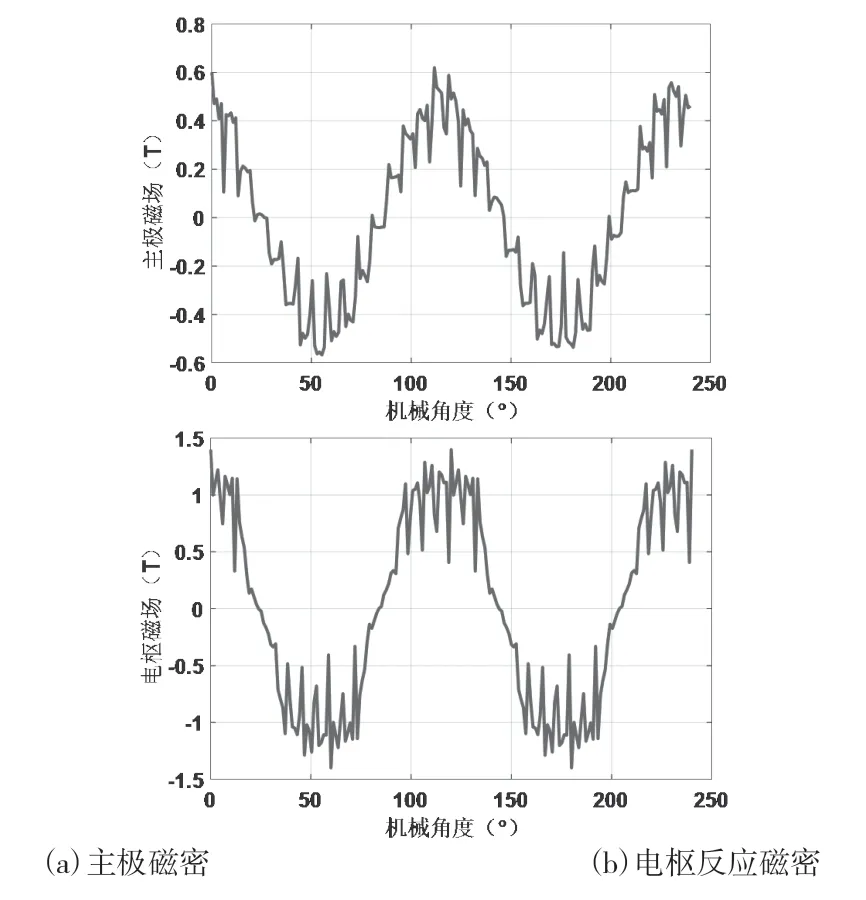
图4 气隙磁密分布

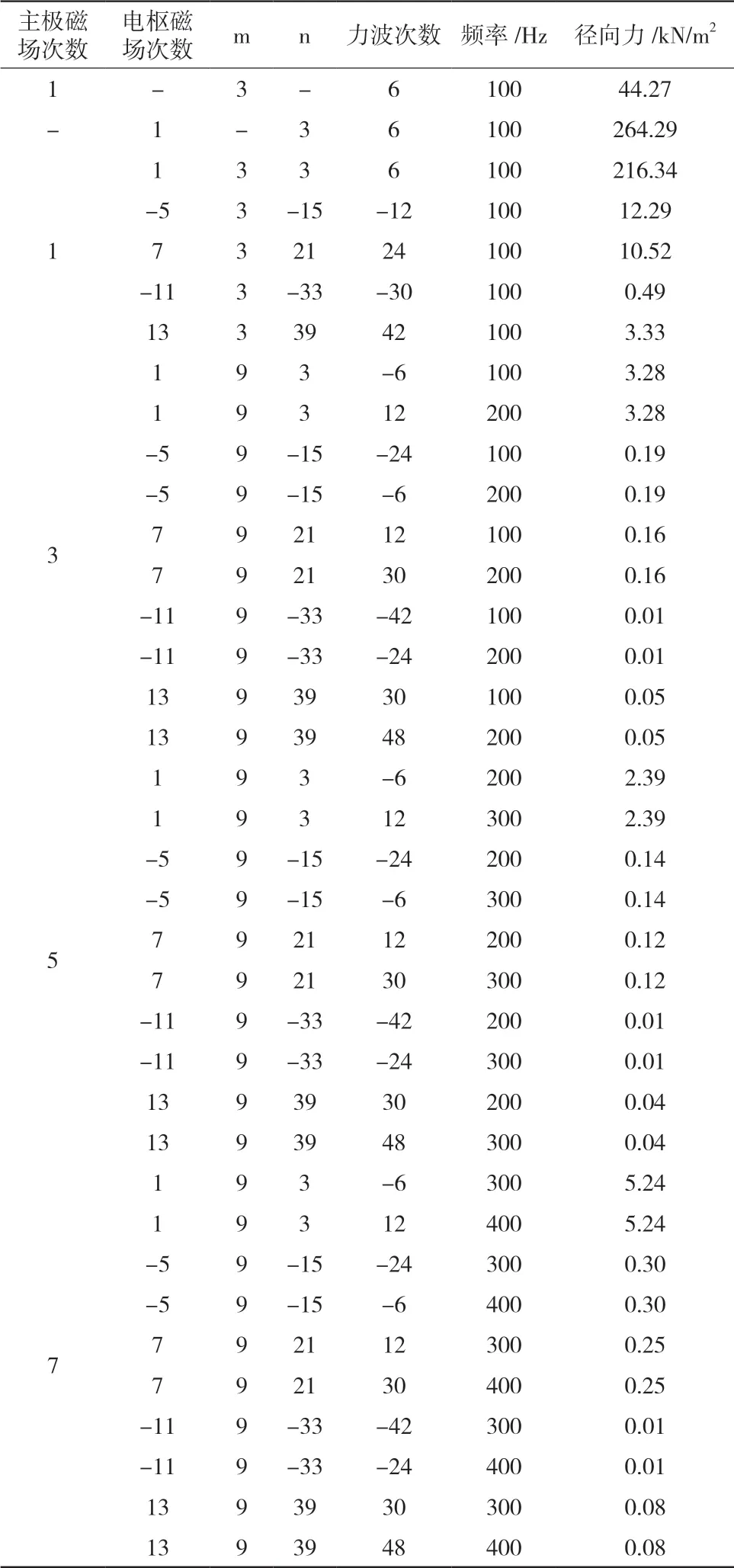
表2 定子铁心径向电磁力计算结果

2.2 固有频率计算

产生的电磁力的振动大小除了与激振力的力波数有关外，还与激振力频率与定子的固有频率接近程度密切相关，如果激振力频率远离固有频率，即使激振力较大、力波数较低亦不会产生大的振动。模态分析是振动分析的特例，也是振动分析的基础，模态分析在振动不受外力的情况，振动分析公式见式（7）所示，模态分析公式如下：

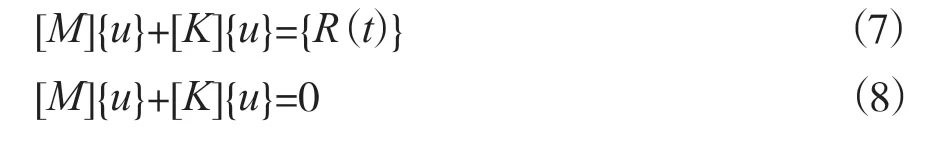
模态分析方程特征值方程为：

式中，[M]为结构的总质量矩阵；[K]为结构的总刚度矩阵；{u}为结构的位移向量；{R（t）}为强迫力列阵。

由上可知，模态方程是振动方程的常系数形态，因此模态方程的解是振动方程的通解。通过对样机进行固有模态分析可初步判断有无共振危险。利用有限元法对样机进行二阶到五阶固有模态分析，得到电机整体的固有模态，如图5所示，二~五阶固有频率如表3所列。

图5 振动模态和固有频率

表3 二~五阶固有频率

从结果可以看出，由于机壳的存在，样机的模态固有频率较高，远离表3中产生振动的电磁力频率，不会造成共振。

2.3 噪声有限元分析

对定子铁心和机壳的形变和等效应力进行仿真分析如图6和图7所示。同时提取机壳外表面速度边界，以声域模型的外表面为噪声表面，在半径为1 m的空气包分析了样机的电磁噪声，如图8所示，标准要求噪声测试在机壳外部1 m处测量，A计权下所产生的噪声值限值为92 dB。

2.4 样机试验结果对比

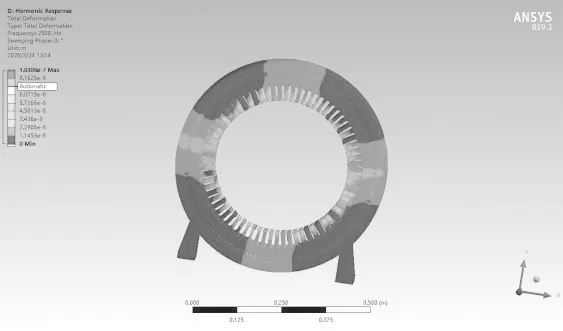
图6 原方案电机定子铁心和机壳形变（1e-7 m）

图7 原方案电机定子铁心和机壳受力（1e5 Pa）

图8 原方案机壳外空气包噪声值（75.97 dB）

可变速抽水蓄能机组由交流励磁电动发电机、三电平变流器、水泵水轮机组成，如图9所示。针对交流励磁电机和三电平变流器的工厂测试实验机组如图10，利用此仿真平台进行了样机的噪声试验。试验条件为电机带载运行，测试人员距离电机1 m处，适用声级计测试电机噪声，环绕一周共测试5个点，测试结果如表4所示。

图9 测试平台示意图

图10 可变速电机和拖动机组

表4 噪声测试数据

由表4中样机试验噪声值和有限元仿真结果可知，仿真较为准确，适用于在电机设计初期进行大量的设计方案对比。

3 样机结构优化

3.1 优化方案径向电磁力计算

本文基于小电机研究，从大电机设计角度出发，仅采用斜槽和在定子齿上开辅助槽（辅助槽局部放大如图11所示）来优化样机的噪声，经过多个优化方案的有限元分析发现，在定子斜槽5°（一个齿距）和定子开半径为1.4 mm辅助槽时优化效果最好。

图11 辅助槽局部放大

计算优化方案的电机定子铁心所受的径向电磁力和优化前的计算结果对比如表5所示。观察表5中定子铁心电磁力的时间和空间分布可以知道，优化方案的定子铁心电磁力有较大的降低，为方便对比分析，绘制不同频率下不同力波的定子铁心电磁力分布如图12所示。由图12可以看出，优化前后定子铁心电磁力的分布基本相同，且各频率和各力波振型下电磁力均有明显降低，说明优化后的方案可以明显降低铁心振动。

表5 定子铁心径向电磁力计算结果

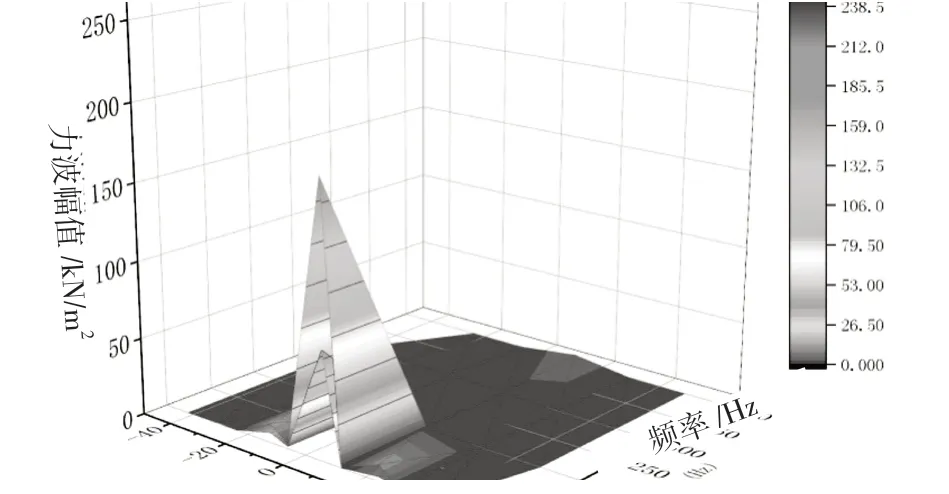
图12 优化前后定子铁心电磁力对比

3.2 优化方案噪声有限元分析

对优化前后定子铁心和机壳的形变和等效应力进行仿真分析如图13和图14所示。同样方法仿真电磁噪声结果如图15所示。

图13 优化后电机定子铁心和机壳形变（6.2 e-8 m）

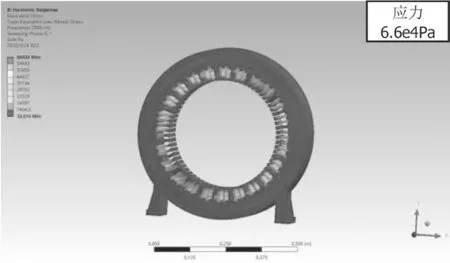
图14 优化后电机定子铁心和机壳受力（6.6 e4 Pa）

图15 优化后机壳外空气包噪声值（66.73 dB）

从上面结果对比可以发现，优化后定子铁心和机壳受力和变形均明显变小，且机壳外空气包噪声也明显较小，由此可见方案优化后电机性能明显提升。样机结构优化前后主要指标对比如表6所列。

表6 结构优化前后主要指标对比

4 结论

本文应用理论结合有限元分析的方法，以1台90 kW可变速发电电动机为研究对象，详细推导了影响电机振动和噪声的径向电磁力计算公式，利用有限元仿真方法计算了样机所受的低频电磁力以及固有频率，分析了其对振动和噪声的影响。并在声学场中有限元仿真了样机的电磁噪声，通过与试验结果对比验证了理论分析方法的正确性。

通过对结构优化发现，多物理场有限元分析计算的方法可以建立电机噪声分析数据库，通过对已有电站的结构形式和噪声试验结果对比分析，可以进一步互联验证所采用分析方法的正确性，本文所采用的结构优化方法有一定的局限性，后续还有很多结构上可以改进的地方，需要进一步在数据库中优化分析。