基于田口方法的抽水蓄能电机空载电压波形影响因素优化分析

尹 熙，朱南龙，朱一枫，张金仙，王 博

（1.国网新源控股有限公司，北京 100052；2.河北丰宁抽水蓄能有限公司，河北 丰宁 068350；3.哈尔滨电机厂有限责任公司大电机研究所，黑龙江 哈尔滨 150000）

0 引言

随着“碳中和”与“碳达峰”重大政策的提出，人们愈发关注能源问题，为加快实现中国能源互联，以较低成本、更快速度达到减排目标，我国在能源改革方面投入不断加大，智能电网便是其中的重要改革方向之一，其依托数据库的支持，实时记录分析电网状态，从而更好地服务于电网，而抽水蓄能电站以其储能、调峰填谷等优势，在大力发展智能电网的今天重要性日益提高[1,2]。作为抽水蓄能电机而言，波形质量是其重要指标之一，该指标直接反映出电压波形的正弦性和谐波情况，谐波不但会在电机内产生损耗、影响效率，还会在用电设备上产生附加损耗，对临近的通信设备产生干扰，而在这一方面的研究，国内外的成果有很多[3,9]，但是往往文献中只研究单一的因素优化，如阻尼条直径对电压波形的影响研究，缺少多个影响因素对波形质量的优化， 因此有必要对此进行研究。

本文采用田口方法，以阻尼槽口宽、阻尼条节距、阻尼绕组对向旋转的距离、极弧半径作为优化因素，以全谐波畸变因数(THD)、电话谐波因数(THF)、磁极极靴处的磁密最大值Bmax作为优化目标，通过建立正交矩阵，并对优化目标进行数值分析， 最终确定最佳方案。

1 发电机的空载电压波形分析方法

发电机空载线电压波形质量可以通过全谐波畸变因数(THD)和电话谐波因数(THF)的数字大小所体现，数字越小其谐波含量越小，表1所示为某台抽水蓄能电机的电机方案设计参数，基于电磁场仿真软件，采用场路耦合时变电磁场有限元方法，对电机空载运行工况进行仿真，获得空载电压波形并对波形进行傅里叶分解，计算得到THD、THF指标大小。

1.1 数学模型及有限元建模

采用二维瞬态电磁场建模，假设位移电流及定子铁心中的涡流忽略不计，定、转子绕组端部电抗通过电路方程和电磁场方程耦合计入，则电机内二维瞬态电磁场方程的边值形式可由式(1)表示。

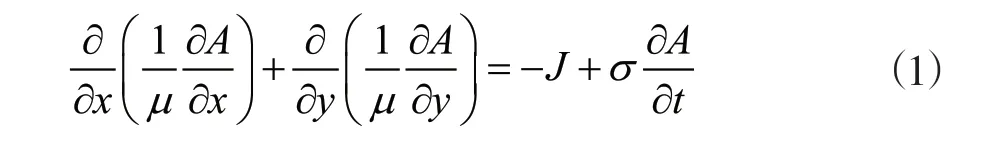
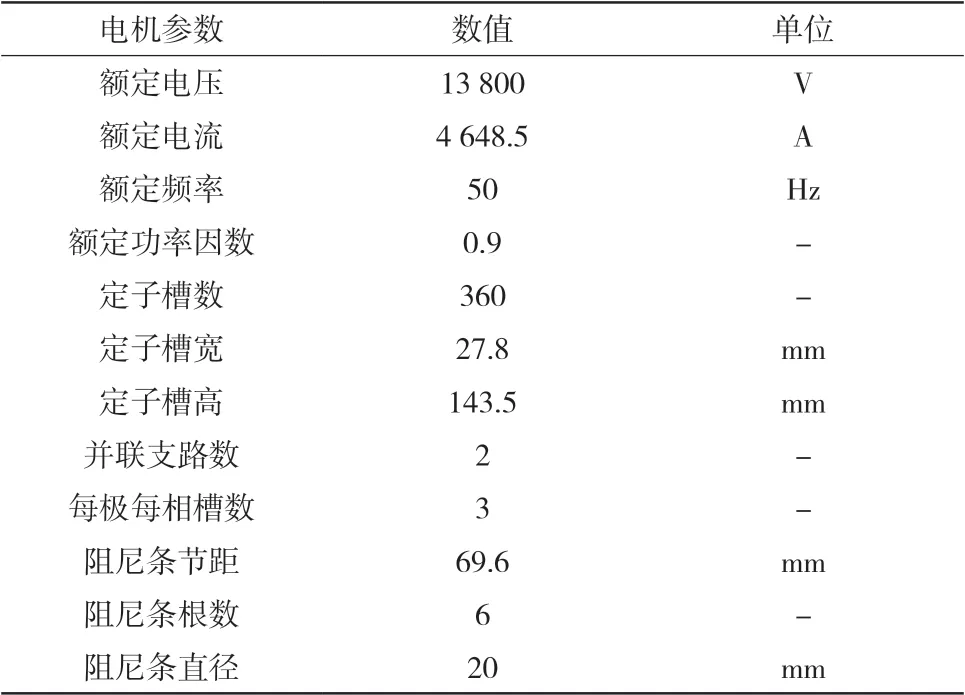
表1 样机主要参数

有限元模型如图1所示。

图1 有限元模型

1.2 THD与THF计算方法

由线电压全谐波畸变因数定义可知，其计算如下：

根据国家标准电话谐波因数计算如下：

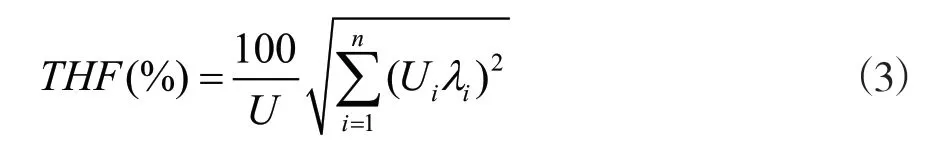
式（2）和式（3）中：U为基波电压有效值；Ui为i次谐波电压有效值；λi为i次谐波的加权系数，不同频率谐波的加权系数可从加权系数表或加权曲线中查出，另外，THF计算应包括额定频率至5 000 Hz频率的全部谐波，且应采用3个线电压中THF最大值者。

1.3 THD与THF结果分析

通过仿真获得了空载磁场分布和线电压波形，分别如图2和图3所示，由图2可以看出电机磁力线由转子磁极进入气隙中，沿着定子齿部进入定子轭部，再分开分别进入临近磁极中，磁力线分布正常，由图3可以看出三相电压也是对称的，因此仿真模型是正确的。

图2 空载磁场分布图

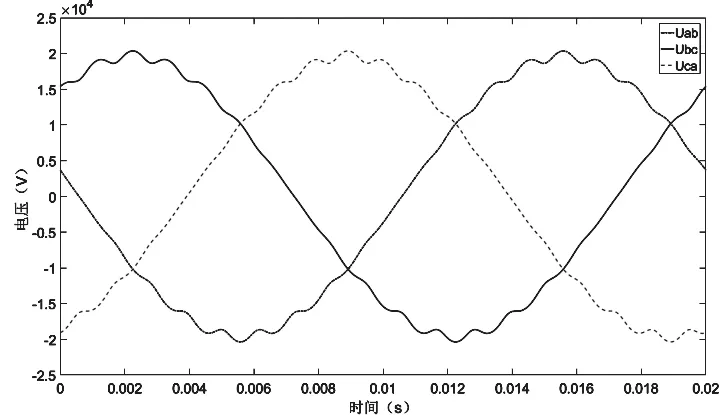
图3 空载线电压波形

对线电压进行傅里叶分析，谐波次数到100次，受文章篇幅所限，本文仅给出了1~32次谐波电压有效值占基波电压有效值的百分比数据如表2所示。

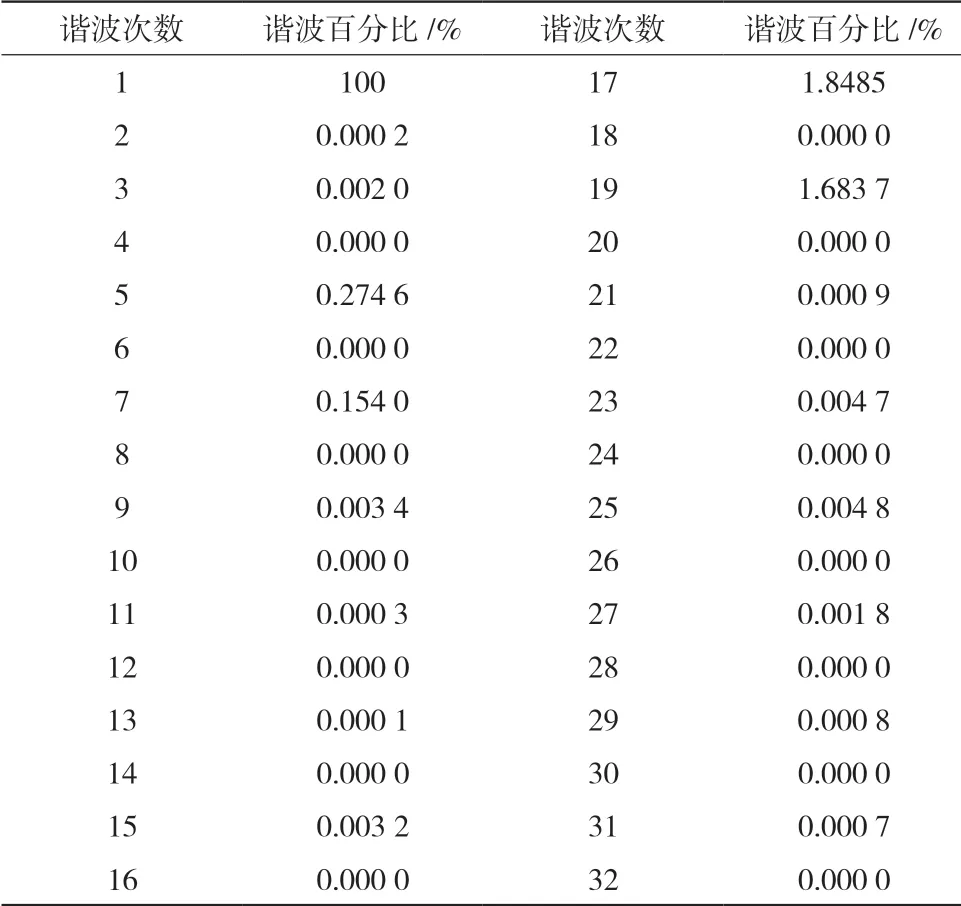
表2 空载谐波电压百分比

由表2可知，谐波次数17次与19次谐波含量相对最高，其次为5次与7次谐波含量较大，根据谐波分析结果以及式（2）和（3）可进一步计算出空载线电压全谐波畸变因数和电话谐波因数，分别为2.527 1%和4.281 2%。从计算结果可见，波形正弦度并不是很好，存在较大的谐波，因此需要对原设计方案进行优化，以获得正弦性更好的波形。

2 田口方法的优化分析

2.1 优化因子、目标及水平值的确定

田口方法是一种可以实现多目标优化的局部优化设计方法，其利用建立的正交表安排试验方法，能够在最少的试验次数中搜索到多目标优化设计时的最佳组合[10]。根据以往文献研究的内容，本文将阻尼槽口宽bs0、阻尼条节距t2bar、阻尼绕组对向旋转的距离L、极弧半径Rps作为优化因子，由于阻尼尺寸的修改可能会引起转子磁极中阻尼条圆心所在弧线的磁密过大，因此将磁极极靴处的磁密最大值Bmax也作为优化目标，提取位置如图4所示，最终以THD、THF、Bmax为优化目标。

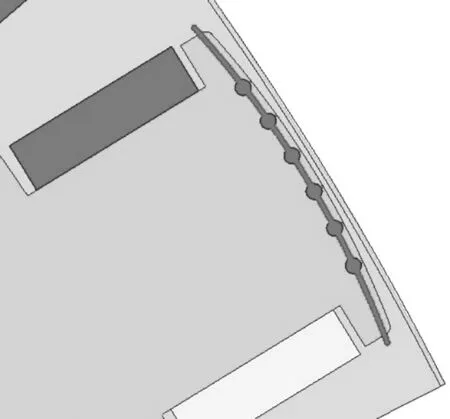
图4 Bmax选取位置图

根据《水轮发电机设计与计算》以及原方案数据，确定优化因子的优选范围，并且在优化范围内等距选取4个优化因子水平值，并按照从小到大的顺序分别取名水平1、2、3、4。每一个优化因子水平数如表3所示。

表3 优化因子水平数

2.2 正交表的确定

正交表是田口方法的关键。正交表的构建有专门的算法，不同因子的排列组合出现的概率都相同。建立正交表时，根据建立的方法不同， 试验次数也不一样， 如果选择方法不当， 会使试验次数增加， 从而增加试验成本。因此合理选择正交表是至关重要的。

正交表一般可以表示为Ln(Ak)，其中:n表示试验次数；A表示水平值数；k表示优化因子个数。例如L16(44)表示有4个优化因子， 每个优化因子选取4 个水平值，共计16次试验。远小于全面试验（44=256）的次数。根据表3以及正交表的构建方法，建立了如表4的L16(44)正交表，并且对每一种方案均进行有限元的仿真。仿真结果也在表4中体现。

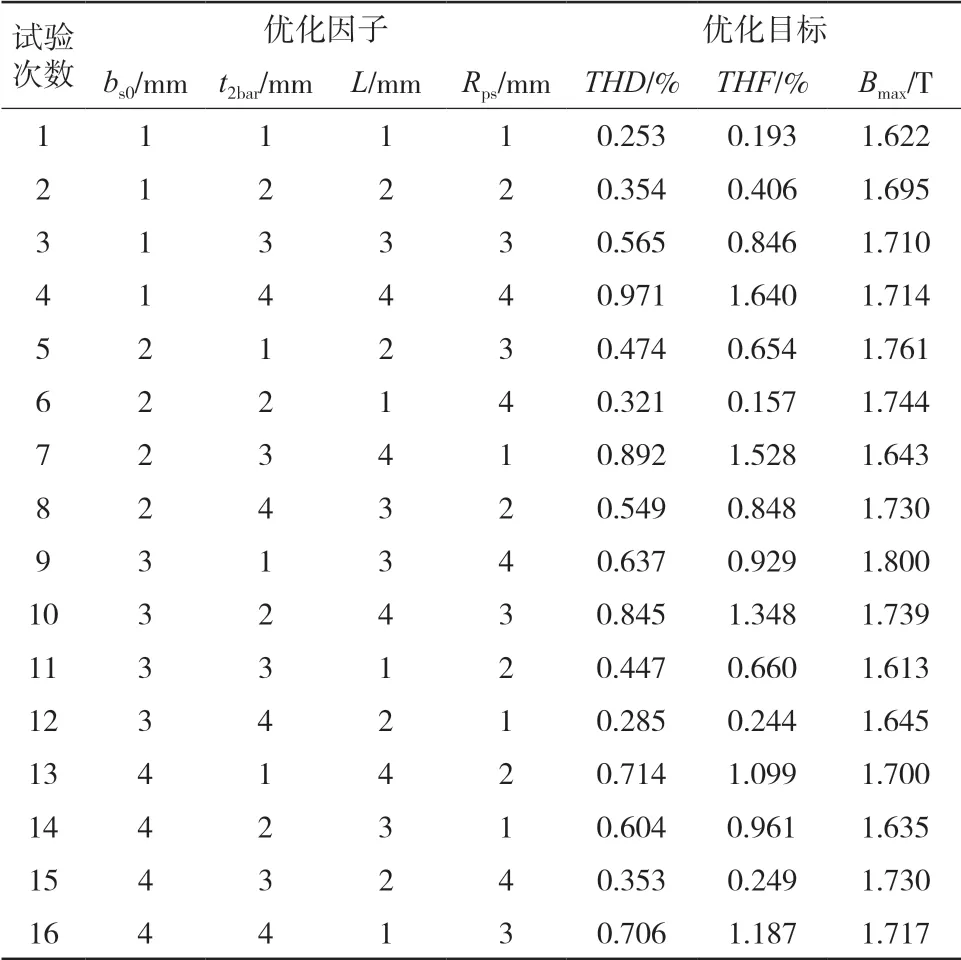
表4 正交表及有限元结果

2.3 数值分析

数值分析包括平均值分析和方差分析。为了分析优化因子的改变对电机优化目标的影响，以及影响所占比重，首先要进行优化因子在不同水平值下的平均值分析。例如THD在阻尼槽口宽bs0在水平2时的平均值为：

式中：THD（bs02）为优化因子bs0在水平2下的数值，THD（1）、THD（2）、THD（3）、THD（4）分为第1、2、3、4次的THD数值。其它优化因子在不同水平值下电机性能指标的平均值也是如此。

其次要进行方差分析，通过方差分析可以分析出优化因子对性能指标的影响比重。计算公式如式（5）、（6）所示。

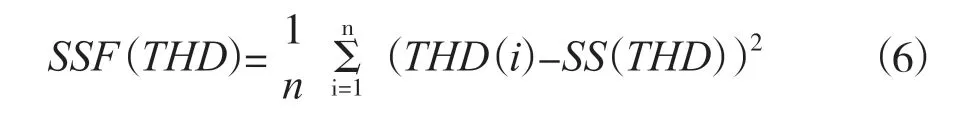
式中：SSF（THD）表示电机THD的平均值；THD（i）表示第i次实验中的THD数值；SSF（THD）为电机THD的方差值；n为各参数水平数。其余优化因子用同样的方法可以得到相应的方差及比重，根据方差分析即可确定出优化因子。

结合表4与公式（4），优化因子在不同水平值下平均值如表5所示，结合表5与公式（5）、（6）可得优化因子在性能指标下的方差及其所占比重，如表6所示。

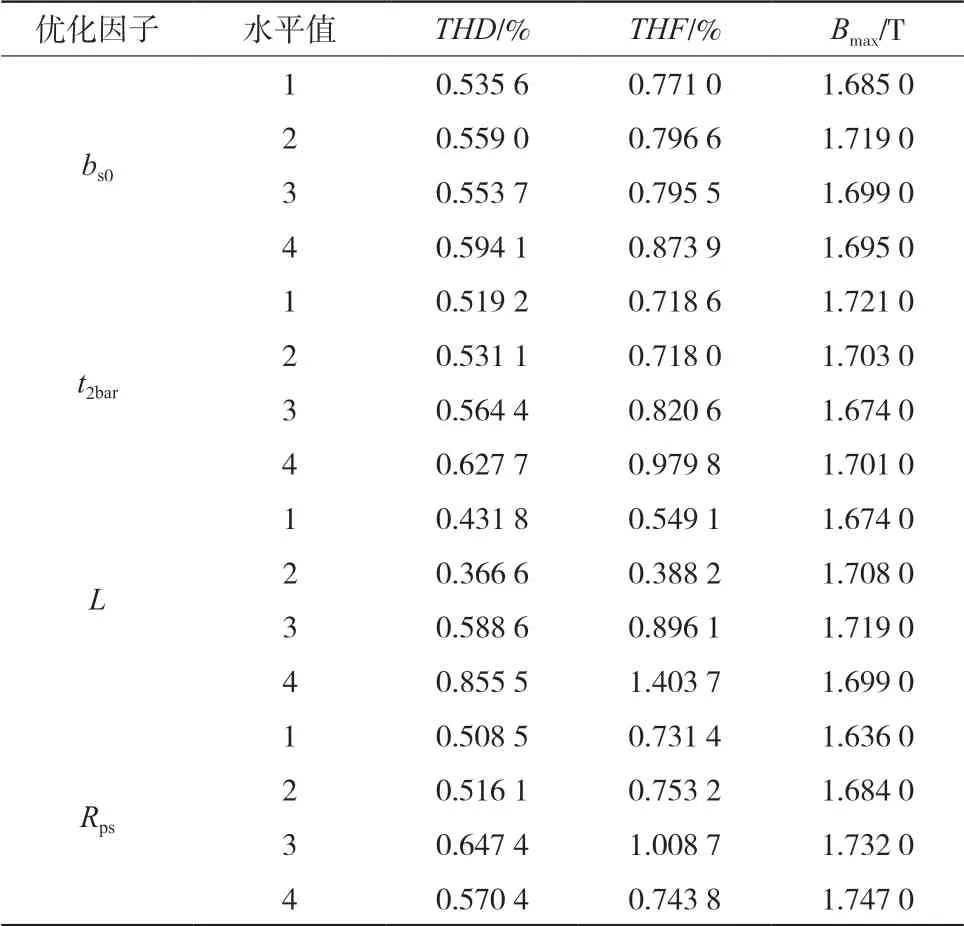
表5 不同水平下的优化目标平均值

表6 各优化因子的方差及比重

由表6可知，L对THD影响最为明显，其次为Rps，L对THF影响也最为明显，Rps与t2bar对THF影响较大，Rps对Bmax影响最大，L与t2bar对Bmax影响较大，根据表5所示，分别使THD最小、THF最小、Bmax最小的组合为bs0（1）t2bar（1）L(2)Rps(1)，bs0（1）t2bar（2）L(2)Rps(1)，bs0（1）t2bar（3）L(1)Rps(1)，通过方差可得，t2bar以Bmax最小为标准，L以THD为标准，最终确定bs0（1）t2bar（3）L(2)Rps(1)为最佳组合方案。

2.4 优化结果对比

根据上节所得的最终优化方案， 建立电机仿真模型，优化方案的电压波形如图5所示，波形正弦性明显提高，对优化后的线电压进行傅里叶分析，同样仅给出了1~32次谐波电压有效值占基波电压有效值的百分比数据如表7所示。也可以明显发现17次、19次谐波大幅降低，5次谐波降低较小，7次谐波基本不变。电机优化前后性能指标对比如表8所示。

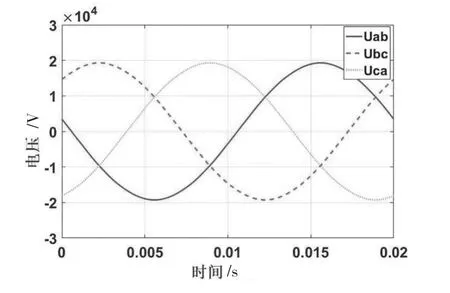
图5 优化后的电压波形

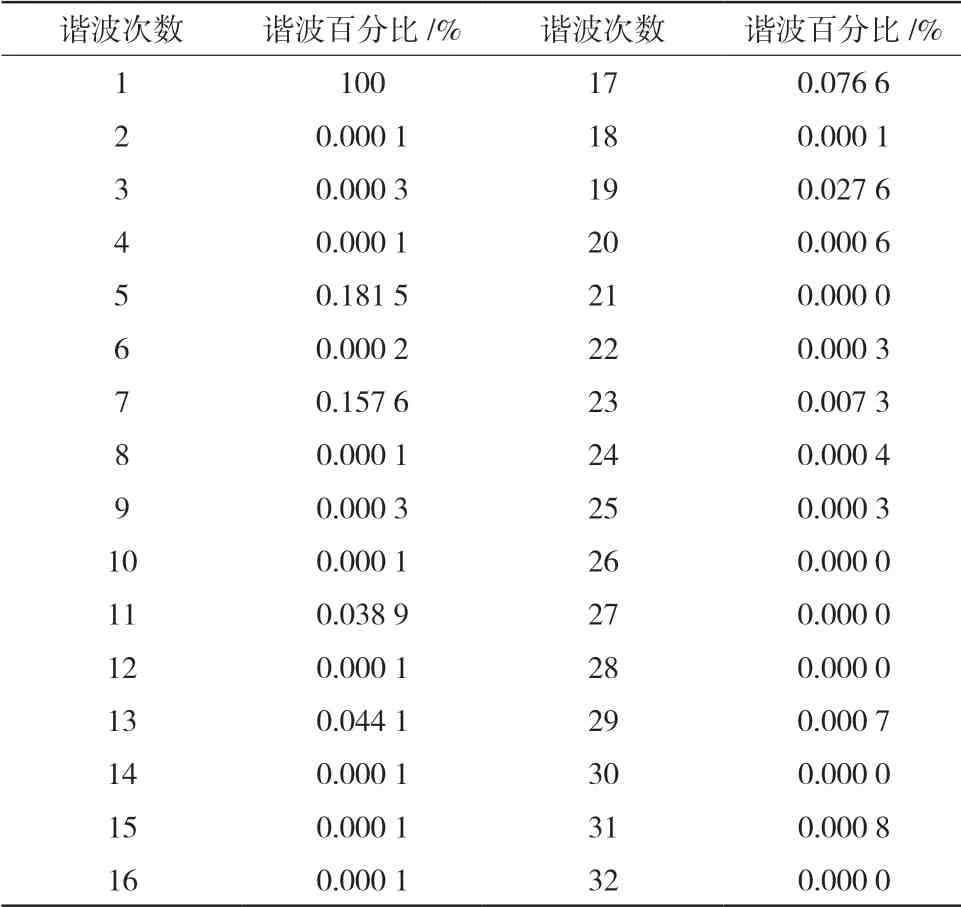
表7 优化后的空载谐波电压百分比

根据表7可知， 优化前后，THD降低了89.6%，THF降低了96.5%，优化效果较明显，Bmax降低了0.03 T,也同样有所降低，达到了优化的目的。

表8 正交表及有限元结果

3 结论

本文采用田口方法，以阻尼槽口宽、阻尼条节距、阻尼绕组对向旋转的距离、极弧半径作为优化因素，以全谐波畸变因数(THD)、电话谐波因数(THF)、磁极极靴处的磁密最大值Bmax作为优化目标对该抽水蓄能电机进行优化。借助有限元方法， 对优化后的电机方案进行二维瞬态电磁场分析，可得如下结论：

（1）原方案中谐波次数17次与19次谐波含量相对最高，其次为5次与7次谐波含量较大。

（2）根据方差分析可知， 阻尼绕组对向旋转的距离L对THD影响最为明显，其次为极弧半径Rps，阻尼绕组对向旋转的距离L对THF影响也最为明显，极弧半径Rps与阻尼条节距t2bar对THF影响较大，极弧半径Rps对Bmax影响最大，阻尼绕组对向旋转的距离L与阻尼条节距t2bar对Bmax影响较大。

（3）利用田口方法对电机进行优化后，THD降低了89.6%，THF降低了96.5% ，优化效果较明显，Bmax降低了0.03 T,也同样有所降低，达到了优化的目的。