传统多高层楼阁式木塔摇摆侧剪行为分析

吴亚杰，宋晓滨

(1.西安建筑科技大学 土木工程学院，西安 710055；2.同济大学 建筑工程系，上海200092)

中国传统木结构具有深厚的历史底蕴，是传统木结构营造技艺的载体，更是中华优秀传统文化的具象表现。随着人们对优秀传统文化日益增长的精神需求，中国传统木结构得到了切实的保护、传承和发扬，各地陆续新建了许多传统风格木结构建筑。作为传统木结构营造技艺的最高成就，多高层楼阁式木塔受到了人们的关注，由于中国是一个地震多发且震害严重的国家，此类结构的设计及其抗震性能有待进一步探讨和研究。

笔者以7层传统楼阁式木塔[14]为对象，基于开源计算软件OpenSees提出了传统楼阁式木塔建模方法，并使用振动台模型试验结果[13]验证其有效性；基于有效的建模方法，考虑不同的摇摆与侧剪切分量组合，建立3种传统楼阁式木塔典型结构数值模型并开展动力时程分析，揭示摇摆与侧剪分量的变化对木塔动力响应的影响。

1 7层传统楼阁式木塔概况

木塔为仿唐楼阁式纯木结构塔，结构平面为正方形，共有7层，每层3开间3进深，底层增设副阶周匝(回廊)，如图1所示。木塔结构高度为40.3 m，其中，底层层高7.35 m，2～6层层高5.25 m，7层楼板至屋顶6.7 m。木塔顶层屋面上设塔刹，高13.4 m，重约10 t，质量主要集中于底部。木塔底层正方形平面宽度17.6 m，2层宽度15 m，2层以上楼层平面宽度每层递减0.6 m。2层及以上楼层外侧走廊宽度为1.2 m。

图1 7层传统楼阁式木塔Fig.1 A traditional seven-story pavilion-style timber

结构中心设有4根贯通塔高的斜柱(亦称金柱，中间有按古法制作的接柱节点，接柱节点见图2，可近似考虑为连续)。斜柱倾斜度为0.37%，通过两道主梁和木支撑组成的桁架和各楼层拉结，形成类似核心框架筒体。外围檐柱底部支承于楼面梁上，上部和斗栱节点通过暗榫相连，每层檐柱内移300 mm，因此，上下楼层檐柱竖向不连续且偏置。斗栱节点与框架筒体形成加强层。木塔底层木柱与下部混凝土柱础相连，并采用木榫头嵌入混凝土卯口的方式限制木柱水平滑移。木塔构件营造方法、节点连接及施工方法详见文献[14]。

图2 接柱节点

结构主要构件均采用非洲花梨木制作，次要局部构件采用柚木，主要构件的几何尺寸信息列于表1。非洲花梨木材性测试结果列于表2。木塔结构总质量约为1 030 t。

表1 木塔主要构件几何尺寸Table 1 The geometric dimensions of main components of timber pagoda

表2 非洲花梨木材性测试结果[15]Table 2 Material property test results of African padauk

2 传统楼阁式木塔建模方法及验证

2.1 梁柱构件的模拟

木梁(核心筒主梁、阑额和楼板梁等)和木柱(金柱和檐柱)截面尺寸较大，这些构件主体在地震作用下未发现破损，保持在基本的弹性状态[13]，因此，在OpenSees数值建模中使用弹性梁柱单元(Elastic Beam Column Element)进行模拟，弹性模型取木材顺纹弹性模量E//。

2.2.1 金柱与相邻木梁的连接 金柱与相邻楼板梁和核心框架主梁均采用半榫连接，如图3所示。使用两节点连接单元(Two Node Link Element)模拟半榫连接。该连接单元设置为零长度，共有6个自由度，分别为沿x、z和y轴(由x轴和z轴根据右手定则确定)的平动自由度和绕x、y和z轴的转动自由度。

图3 半榫节点连接模拟Fig.3 Connection simulation of half tenon

根据Luo等[15]完成的半榫节点试验结果，考量半榫节点转动刚度对木梁内力的影响，如图4所示。试验木梁截面尺寸为100 mm × 150 mm，节点初始转动刚度试验值k为71.64 kN·m/rad，对于跨度相同(按照缩尺比例计算约为1.4 m)的两端刚接木梁、半刚性连接(半榫连接)木梁和两端铰接木梁，在

图4 半榫节点弹性转动刚度对木梁内力的影响Fig.4 Influence of elastic rotational stiffness of half tenon joint on the internal force of wood

跨中单位集中力的作用下，半榫连接木梁跨中弯矩为两端铰接木梁的94.8%，可见，半榫连接转动刚度对梁内力影响较小，属于“柔性”连接，故节点平面内(绕y轴)和平面外(绕z轴)的转动刚度取一较小值(即铰接处理)；其余自由度因受到相对较强的约束，其刚度假设为无穷大(通过设置一个显著大的值实现)。

2.2.2 楼板梁之间的连接 结构各层楼板梁一端相交于4根芯柱，另一端和楼板边梁相交后延伸至结构外部作为挑台梁，楼板梁与楼板边梁在交汇点处搭接。由于楼板梁的作用主要是承担楼面荷载并将其传递到相邻金柱或斗栱节点上部的叉柱上，对整体结构的抗侧刚度影响较小，且试验中楼板梁没有破坏。因此，在对楼板梁进行建模时，将楼板梁和楼板边梁的搭接节点假设为刚接节点，而楼板梁和芯柱的连接设为铰接，如图5所示。挑台部分及其荷载简化为集中力作用在刚接节点上。

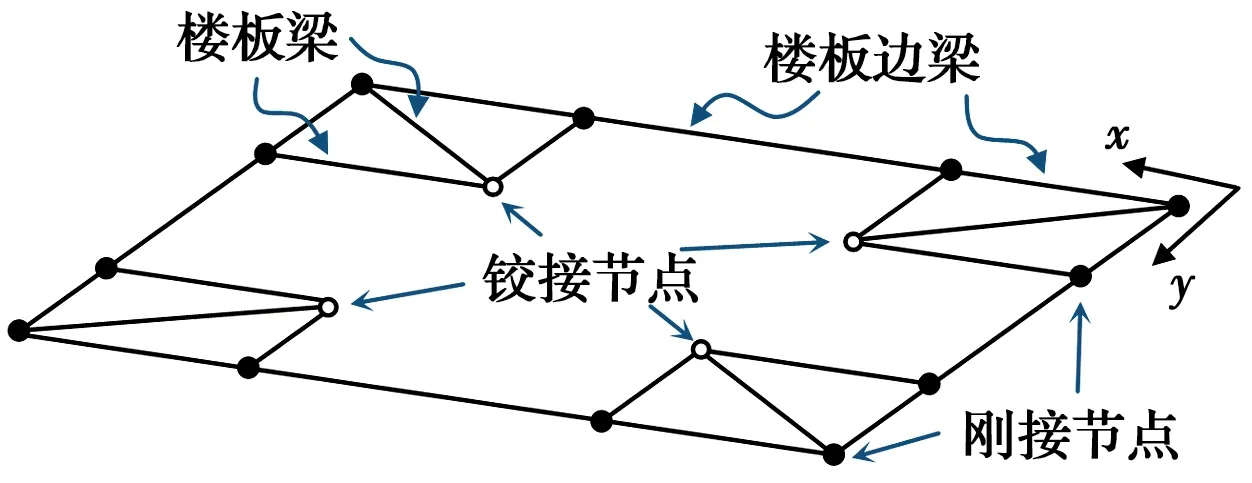
图5 楼板梁连接的处理Fig.5 Modelling of floor beam

2.2.3 檐柱顶部和底部与木梁的连接 檐柱柱脚叉放在楼板梁上，其顶部与阑额通过燕尾榫相连。檐柱的摇摆抗侧和梁柱连接的抗弯性能均为榫卯连接木框架抗侧性能的重要组成。然而，对以上两部分连接独立模拟会显著增加结构模型的复杂度，因此，将这两部分提供的抗侧性能使用宏观剪切弹簧模拟，则檐柱顶部和底部与木梁的连接设为铰接。因此，檐柱在数值模型中只传递竖向荷载。

2.2.4 斗栱节点的抗压性能模拟 斗栱节点既承担竖向荷载又具备抵抗侧向荷载的能力，其中，在模拟斗栱节点竖向抗压性能时，考虑到其弹性抗压承载力[10]远大于其在木塔结构中承担的竖向荷载，因此使用两端弯矩释放的弹性梁柱单元模拟。斗栱节点主要为横纹受压，故该弹性梁柱单元的弹性模量取木材横纹弹性模量E⊥(取表2中径向和切向弹性模量的均值)。斗栱节点竖向抗压刚度与木枋在枦斗底面积范围内交错的面积有关，因此，根据斗栱节点抗压试验结果[10]，弹性梁柱单元的面积近似取为栌斗有效受压面积0.3Ab0，Ab0如图6阴影部分所示，其中，Wb为木枋截面宽度，lct为栌斗顶面宽度，单元高度取斗栱节点高度。

图6 栌斗有效受压面积Ab0Fig.6 Effective compression area of

2.3 柱架层和加强层抗侧性能模拟

将一榀榫卯连接木框架或双斗栱节点作为一个整体考虑，使用单个剪切弹簧模拟其抗侧性能，如图7所示。剪切弹簧基于两节点连接单元(Two Node Link Element)定义。考虑到中间跨和边跨构件所承担的竖向荷载差异以及结构的对称性，除底层外，第i层柱架层或斗栱加强层分别可定义中间跨弹簧km,i和边跨弹簧ke,i两类弹簧。

图7 柱架层或加强层抗侧性能模拟Fig.7 Modelling of the lateral performance of beam-column

图8 滞回模型[16]

表3 缩尺结构各层榫卯连接木框架抗侧骨架曲线参数取值Table 3 Parameter values of backbone curve of timber frames in each story of scaled model

表4 榫卯连接木框架抗侧滞回规则系数取值Table 4 Values of coefficients in defining hysteretic rules of timber frames

表5 缩尺结构各层斗栱节点抗侧骨架曲线参数取值Table 5 Parameter values of backbone curve of dou-gong connections in each story of scaled model

表6 斗栱抗侧滞回规则系数取值Table 6 Values of coefficients in defining hysteretic rules of dou-gong connections

2.4 木支撑刚度计算方法及模拟

木支撑的连接形式如图9所示。由于木材横纹方向材性显著弱于顺纹方向材性，木支撑变形主要源自榫头的斜纹受压变形、木柱和木梁表面的横纹受压变形。

因支撑竖向抗压刚度对结构整体抗侧刚度影响较小，故侧重于木支撑水平抗侧刚度kb，可通过式(1)计算。

(1)

式中：kt为榫头斜纹抗压刚度,kN/mm；kc为木柱柱体横纹抗压刚度,kN/mm。

参考Chang等[18]的研究，榫头斜纹抗压刚度kt可根据榫头接触面积、榫头长度和力与顺纹反向的角度计算。

(2)

(3)

A1=btht

(4)

式中：E(θ)为斜纹弹性模量，MPa；θ为力与顺纹方向的夹角,rad；系数n可取2；bt为榫头截面宽度,mm；ht为榫头截面高度,mm；lt为榫头长度,mm。

木柱横纹抗压刚度kc可根据支撑底部接触面积和木柱直径近似计算。

(5)

A2=hclb

(6)

式中：hc为接触高度,mm；lb为支撑截面宽度,mm。

由于结构在地震激励下会产生往复位移，结构一侧木支撑在结构动力响应中会出现与木柱和主梁脱离接触的情况，此时支撑抗侧刚度为零。为简化计算，使用剪切弹簧对每个支撑进行建模，但弹簧刚度折减50%。

在1/5缩尺木塔结构中，图9中lt=62 mm、bt=11 mm、lb=34 mm、ht=hc=10 mm、θ=45°、D=130 mm。原型结构支撑相关尺寸可根据缩尺比例换算得到。

图9 木支撑的连接方式Fig.9 Jointing details of the

2.5 建模方法验证

基于以上提出的建模方法，建立7层传统楼阁式木塔模型结构的有限元数值模型，如图10所示。结构数值模型采用集中质量，集中质量来源于3部分：第1部分为结构构件的自重，可在OpenSees中通过设置单元密度自动计算，质量平均分配在单元的两个节点上；第2部分来源于楼面荷载，按照各节点承担的荷载面积计算总荷载并且转化为质量，均匀分布在楼板四角点；第3部分是来源于简化建模省略的构件重量及荷载，如楼板外挑部分和斗栱支承的挑檐及其所承担的荷载，均转化为相应外部节点上的质量。

数值模型和缩尺结构的自振频率对比列于表7。由表7可见，数值模拟得到的各阶自振频率均低于试验结果。一方面，模型结构构件众多、连接关系复杂，白噪声激励下结构侧移较小，相关节点(例如榫卯节点)仍处于紧密连接状态或摩擦力作用，因而刚度和自振频率较高；另一方面，数值模型采用了简化建模方法，没有考虑摩擦力影响，对构件和节点的初始段刚度模拟精度较差，因此，自振频率模拟结果较低。

表7 木塔缩尺结构与数值模型自振频率对比Table 7 Comparison of natural frequencies of scaled pagoda and numerical model

考虑不同地震强度作用，开展木塔缩尺结构非线性动力时程分析，获取各层加速度和位移时程反应，并与振动台模型试验结果[13]进行对比。以上海人工波(SHW2)工况(振动台试验加速度相似系数为2.0)为例，图11和图12分别对比了七度多遇(0.07g)、七度基本(0.2g)和七度罕遇(0.44g)SHW2激励下数值模型和缩尺结构的加速度放大系数和层间位移角分布(最大值组合)。

图11表明数值模型各楼面加速度放大系数与试验结果均吻合较好，但塔刹加速度放大系数比试验结果小，说明结构顶部楼层或塔刹与主体结构连接区刚度较数值模型小。图12中数值模型上部楼层层间位移角较试验结果小，且其差异随着地震激励强度增加而增大，说明数值模型上部楼层刚度较试验结构大，地震作用下非线性响应较弱，但数值模拟结果能够较为真实地反映结构底层的最大位移角，其原因在于数值模型的加速度和位移时程的最大值与试验值较为接近(以图13为例)。因此，提出的建模方法可用于计算楼阁式木塔的动力响应。

图11 SHW2激励下加速度放大系数分布对比Fig.11 Comparison of acceleration amplification coefficient distribution under

图12 SHW2激励下层间位移角分布Fig.12 Maximum inter-story drift distribution along model height under

图13 七度罕遇(0.44g)SHW2木塔4层楼板动力响应对比Fig.13 Comparison of dynamic responses of the fourth floor under SHW2 with rarely-met

3 摇摆与侧剪行为分析

为定性地研究结构摇摆与侧剪分量对结构整体抗震性能的影响，在图1所示结构方案的基础上，通过改变结构布置方式或相关构件连接参数，变化得到不同摇摆与侧剪分量构成的典型木塔结构。典型木塔结构特征列于表8。

表8 不同摇摆与侧剪分量构成的典型木塔结构Table 8 Typical timber pagoda structures with different rocking and racking components

木塔结构Ⅰ为图1所示原型结构，结构中外围榫卯连接木框架和斗栱节点表现为摇摆与剪切协同抗侧，核心筒框架为剪切抗侧机制。以木塔结构Ⅰ作为基准结构。

木塔结构Ⅱ在保持木塔结构I几何特征不变的基础上，将核心筒框架还原为榫卯连接木框架和斗栱节点，使整个结构变化为更具宋辽特色的“柱架层+铺作层”的结构布置方式(类似应县木塔的结构特点，即木塔结构Ⅱ中心与结构I外围布置相似)。相对木塔结构I，木塔结构Ⅱ增加了木柱和斗栱的摇摆抗侧分量，从整体上削弱了剪切抗侧分量。

木塔结构Ⅲ将核心筒框架梁与框架柱节点的连接刚度增大，由柔性连接改为刚性连接，其他结构构件和布置方式均保持不变。刚性梁柱节点增加了核心筒框架的抗侧刚度，从而增加了结构的侧剪分量。

木塔结构Ⅰ～Ⅲ的数值模型根据前述木塔建模方法建立。除结构自重外，数值模型的重力荷载代表值及模型质量分布主要取决于挑檐、楼面的恒载和活载，其设计面荷载列于表9。

表9 典型木塔结构设计面荷载Table 9 Design surface load of typical timber pagoda structures

3种典型结构外围榫卯连接木框架和斗栱节点抗侧性能参数分别列于表10和表11。因木塔结构Ⅱ改为传统“柱架层+铺作层”的结构布置方式，结构中心榫卯连接木框架和斗栱节点性能参数列于表12和表13。

表10 典型结构外围榫卯连接木框架抗侧骨架曲线参数取值Table 10 Parameter values of backbone curve of external timber frames in each story of typical structures

表11 典型结构外围斗栱节点抗侧骨架曲线参数取值Table 11 Parameter values of backbone curve of external timber frames in each story of typical structures

表12 木塔结构Ⅱ中心榫卯连接木框架抗侧骨架曲线参数取值Table 12 Parameter values of backbone curve of central timber frames of structure Ⅱ

表13 木塔结构Ⅱ中心斗栱节点抗侧骨架曲线参数取值Table 13 Parameter values of backbone curve of central timber frames of structure Ⅱ

仅讨论分析摇摆与剪切抗侧分量配比对结构抗震性能的影响，因此根据木塔结构所在场地(Ⅳ类场地)，选取上海人工波作为地震输入，地震强度主要考虑七度多遇、七度基本和七度罕遇地震强度，开展动力时程分析。

续表10

3.1 结构自振频率

各典型木塔结构的自振频率列于表14。由于增加了核心筒框架梁柱节点的刚度，木塔结构Ⅲ的自振频率大于木塔结构I。木塔结构Ⅱ的一阶自振频率与木塔结构I大致相当，二阶自振频率比木塔结构I稍高(约提高13%)，这是因为木塔结构I中核心筒框架各层梁柱节点均设为铰接，且芯柱与地面连接也设为铰接，在此边界约束下的通长核心筒柱(金柱)抗侧刚度较小，而将其还原为传统的“柱架层+铺作层”的结构布置方式后，各层木柱和斗栱在竖向荷载作用下的摇摆抗侧刚度增加，结构整体刚度有略微增加。

表14 典型木塔结构自振频率对比Table 14 Comparison of natural frequencies of typical timber pagoda structures

3.2 结构加速度放大系数分布

各典型结构的加速度放大系数分布如图14所示。在七度多遇地震作用下，由于结构非线性发展不明显，木塔结构Ⅰ和Ⅱ的加速度放大系数分布相近；木塔结构Ⅲ因刚度较大，各层的加速度放大系数大于其他结构。在七度基本地震作用下，木塔结构Ⅱ的4层以上的加速度放大系数明显大于木塔结构Ⅰ，但与木塔结构Ⅲ相近(除塔刹外)；在七度罕遇地震作用下，木塔结构Ⅱ的2～6层的加速度放大系数大于木塔结构Ⅰ；以上加速度放大系数增大的原因为底层在中震和强震作用下进入非线性(图15(c)木塔结构Ⅱ层间位移大于木塔结构Ⅰ)。可见，摇摆分量的增加会影响结构在不同强度地震作用下的加速度响应；侧剪分量的增加使得结构刚度增加，从而会放大结构的加速度放大系数。

图14 各典型木塔结构加速度放大系数对比Fig.14 Comparison of acceleration amplification coefficient of the typical timber pagoda

3.3 结构层间位移角分布

图15为各典型木塔层间位移角分布对比。虽然木塔结构Ⅲ核心框架节点采用了刚接节点，但总体变形为剪切变形。各典型木塔结构的层间位移角沿结构高度方向变化规律相似，均在结构底层出现最大层间位移角。此外，由于木塔结构Ⅲ刚度较大，其各层(除第3层)层间位移角比结构Ⅰ和结构Ⅱ小。木塔结构Ⅱ相比木塔I增加了斗栱铺作层和木柱的摇摆分量，因而在小震下的层间位移角小于模型结构Ⅰ。随着地震强度的增加，木塔结构Ⅱ底层榫卯连接木框架和斗栱铺作层进入非线性，底层总抗侧刚度降低，导致底层位移角逐渐超过木塔结构Ⅰ，而上部楼层的框架层和铺作层刚度退化较不明显，因而层间位移角比木塔结构Ⅰ小。

图15 各典型木塔结构层间位移角分布对比Fig.15 Comparison of inter-story drift distribution of the typical timber pagoda

值得注意的是，木塔结构Ⅱ在第3层的层间位移角在3种地震烈度下均小于木塔结构I和Ⅲ，尤其在大震(七度罕遇)下的差异最为明显。可能的原因是增加的铺作层在第3层达到刚度和耗能的平衡，即木柱和斗栱摇摆对于刚度的贡献和斗栱耗能对于降低非线性侧移贡献的最优体现。

3.4 结构层间剪力分布

各典型木塔结构的层间剪力分布对比示于图16。木塔结构Ⅲ的层间剪力大于其他结构，说明结构侧剪分量的增加会增大结构的层间剪力。木塔结构Ⅱ的2～6层的层间剪力大于木塔Ⅰ，但随着地震强度的增加，层间剪力的差值增大。七度罕遇地震作用下，木塔结构Ⅱ7层层间剪力小于木塔结构Ⅰ。

图16 各典型木塔结构层间剪力分布对比Fig.16 Comparison of inter-story shear force distribution of the typical timber pagoda

由此可见，增加侧剪分量能够增加结构的层间剪力；而摇摆分量的增加使得结构上部楼层层间剪力减小，下部楼层层间剪力增大。

4 结论

通过改变结构相关布置方式或构件连接性能参数，揭示了摇摆分量和侧剪分量对木塔结构抗震性能的影响，主要结论如下：

1)木塔结构中摇摆分量与侧剪分量耦合抵抗地震荷载作用，且摇摆与侧剪分量比影响木塔结构的抗震性能。

2)增加结构的侧剪分量能增强结构的刚度，从而减小结构在不同地震强度下的位移反应，但同时会增大结构的加速度放大系数和层间剪力。

3)增加结构的摇摆分量会增加结构底层的非线性反应，从而引起结构层间位移角和加速度放大系数分布规律的改变：随着地震强度的增加，结构下部楼层层间位移角增大，上部楼层层间位移角减小；结构上部楼层加速度放大系数呈先增大后减小趋势；顶部楼层层间剪力减小，其他楼层层间剪力增大。