汽轮机侧机网耦合系统低频振荡特性与抑制策略研究

冯鼎元，康英伟

(上海电力大学 自动化工程学院，上海 200090)

0 引言

现阶段，新能源大规模并网是电力系统响应“碳达峰、碳中和”政策的必然需求，低频振荡是新能源高渗透背景下影响电网稳定运行的关键因素[1]，因其涉及转子转速和功率的波动，也被称为机电振荡[2]。励磁侧电力系统稳定器(power system stabalizer，PSS)是现代电厂抑制低频振荡的必要配置，但风电、光伏等新能源的接入导致传统同步发电机的励磁侧PSS阻尼抑制效果下降[3]，给传统火电机组动态稳定运行带来了全新挑战[4]。

为提升系统稳定性，在进一步提升PSS性能[5-6]的同时，研究人员基于灵活交流输电系统技术[7]和附加阻尼控制[8]等方法展开研究。随着原动机调节系统响应特性快速提升，为从原动机侧提升系统阻尼，文献[9]基于负阻尼理论设计出调速侧电力系统稳定器(governing side power system stabalizer，GPSS)，为提升系统稳定性提供了全新的手段。

相较于PSS，GPSS因安装于调速侧而不参与多机间的阻尼交互，在多工况下的鲁棒性更强，并具有优异的多机解耦性[10]。GPSS优化设计时，PSS的设计方法具有借鉴意义，文献[11]对原动机调速系统阻尼特性进行机理分析，并参照PSS的相位补偿方法设计GPSS，在多机系统验证了GPSS的低频振荡抑制性能。但基于传统相位补偿方法的GPSS配置存在全局状态方程难以获取[12]、其他运行状态下的鲁棒性难以保证[13]等问题。群智能算法的全局优化能力为GPSS参数整定提供了新思路，针对传统控制理论难以有效解决的控制器参数非线性多维优化问题，文献[14-17]采用了粒子群算法、禁忌搜索算法和帝国竞争算法等人工智能算法，对阻尼控制器的超前滞后环节进行了优化整定，使得系统阻尼特性得到改善。

蚁狮算法(ant lion optimizer，ALO)于2015年被提出，作为一种新型群智能寻优算法，在电力行业的风电储能容量配置[18]、光伏设备管控[19]等领域已有应用先例，但在以特征值作为中间函数的多维非线性GPSS优化中，ALO还尚未应用。为从汽轮机侧对负阻尼型低频振荡进行抑制，本文使用机网耦合Phillips-Heffron模型进行机械阻尼机理分析。为补偿汽轮机给系统带来的负阻尼，区别于传统设计中的相位补偿法，对制约ALO算法寻优性能的适应因子分段线性特性和蚁狮移动步长恒定两个问题进行改进，使用改进型ALO算法优化设计GPSS，通过蚁狮的全局搜索能力提升系统的阻尼性及鲁棒性。

1 机网耦合系统机理分析

1.1 汽轮机及其调速系统模型

机网耦合分析时，汽轮机传递函数Gst(s)中不考虑中间再热环节及低压联通管的影响，用高压蒸汽室容积时间常数TCH代替。调速系统侧忽略油动机开启关闭的不同时间常数，用时间常数Tg代替，Ka为调速系统增益。汽轮机侧模型如图1所示。

图1 汽轮机侧模型

1.2 机网耦合Phillips-Heffron模型

建立含有汽轮机侧模块的机网耦合模型，在传统Phillips-Heffron模型[20]中考虑转子受到的机械转矩Tm的动态变化，加入机组机械转矩动态变化方程，并将其在稳态运行点线性化，得到将状态变量以增量Δ表示的机网耦合小扰动分析模型：

(1)

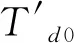
将系统稳态运行点的具体参数值代入，常量部分用K1～K6表示，K1～K6反映电力系统的网络结构、负荷特性等性质，推导过程参见文献[20]。式(1)对应的机网耦合Phillips-Heffron模型如图2所示。

图2 机网耦合Phillips-Heffron模型

将图2的传递函数模型写成状态空间表达式：

(2)

其中：

1.3 机械阻尼转矩分析

机械阻尼转矩是对励磁系统阻尼转矩理论的拓展，旨在参照电磁功率分析方法对机械功率进行机理分析，文中统称为阻尼转矩理论。

由式(1)的前2个微分方程得：

(3)

电磁转矩增量ΔPt表达式为：

(4)

同步转速下，转子受到的机械转矩Tm与发电机输入机械功率Pm相等，将式(4)代入式(3)中：

(5)

(6)

根据阻尼转矩理论，将ΔTm与ΔTe分解为：

ΔTe=TdeΔω+TseΔδ

;

(7)

ΔTm=TdmΔω+TsmΔδ

，

(8)

其中：Tde和Tdm分别为机械阻尼转矩系数和电磁阻尼转矩系数；Tse和Tsm分别为机械同步转矩系数和电磁同步转矩系数。将ΔTm与ΔTe按阻尼转矩法分解后代入式(6)，求得系统的特征方程：

Ms2+(D+Tde-Tdm)s+ω0K1+ω0(Tse-Tsm)=0

。

(9)

方程解(9)中的共轭特征值称为系统的机电振荡模式，记为λs=ζs+jωs，s=1，2，3，…，n。s为各振荡模式序号。λs的实部解：

(10)

ζs对应系统微分方程时域解中的指数部分，决定了系统阻尼特性。若汽轮机侧期望为系统提供正阻尼，-Tdm整体须为正值。

1.4 阻尼转矩与同步转矩数值求解

记ΔTe=Fe(s)Δδ，ΔTm=Fm(s)Δδ，Fe(s)与Fm(s)是Δδ到ΔTe、ΔTm的传递函数。式(6)变为：

(11)

系统的特征方程为：

Ms2+Ds+ω0K1+ω0Fe(s)-ω0Fm(s)=0

。

(12)

当Fe(s)与Fm(s)已知，由式(13)可求得阻尼转矩与同步转矩分量具体数值[21]：

(13)

1.5 实例模型数值分析

某汽轮机模型的单机无穷大系统中，设发电机阻尼系数D=0，其稳态运行参数见表1，系统模型如图3所示。

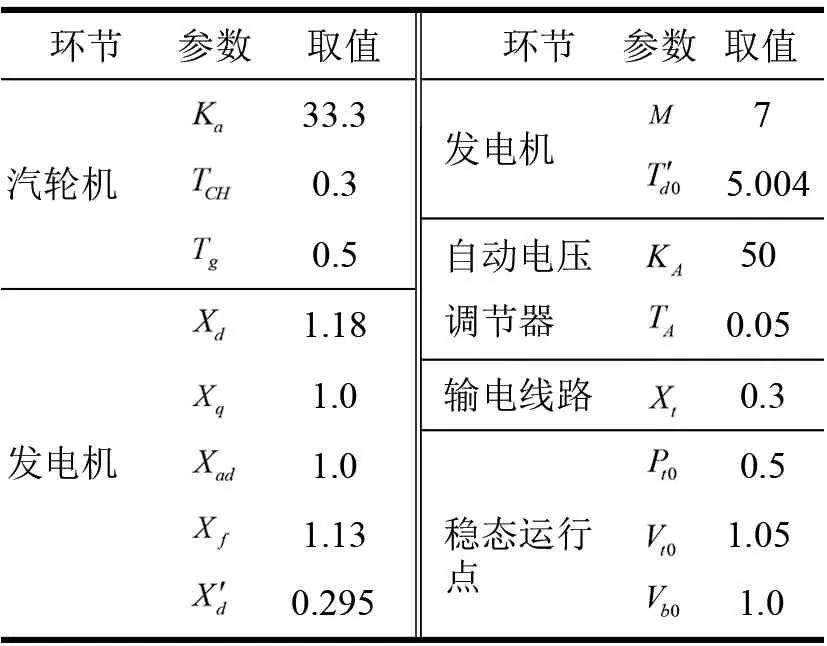
表1 系统运行参数(标幺值)

图3 单机无穷大系统模型

整定计算求得：

K1=1.111 7,K2=0.809 4,K3=2.466 7,K4=0.712 3,K5=0.012 3,K6=0.467 3。

此时，电力系统状态方程为：

状态矩阵的特征值为：

λ1,2=0.125 8± j7.198 1，λ3=-12.03，λ4=-8.28，λ5=-1.488 6，λ6=-4.217 9。

低频振荡对应状态矩阵特征值中的共轭解，λ1,2=0.125 8± j7.198 1为该系统的机电振荡模式。系统的Fe(s)与Fm(s)由传递函数框图求得，利用式(13)计算Tde、Tdm、Tse和Tsm：

该运行方式下，电磁功率为系统提供的阻尼转矩Tde=1.217 5，机械功率提供机械阻尼转矩-Tdm=-3.22，汽轮机侧削弱了系统的阻尼。若不考虑原动机侧影响，忽略表1中汽轮机参数，系统小扰动分析模型由6阶降为4阶，系统特征值为：

λ1,2=-0.078 5± j7.017 6，λ3=-12.031 5，λ4=-8.300 5。

此时λ1，λ2解的实部为接近零的负值，物理表现为系统受到扰动时Δδ的振荡收敛较慢。而机网耦合系统中，由于汽轮机为系统带来了负阻尼，机电振荡模式由复平面的左半平面转移至右半平面，受到扰动时，Δδ的发散波动将导致发电机输出有功功率呈现发散振荡。

上述分析表明，系统稳定裕度不足的情况下，汽轮机侧实际运行参数设置不合理，将对系统稳定性产生决定性影响。

2 基于改进ALO算法的GPSS设计

2.1 GPSS模型

GPSS是加装于原动机调速侧的稳定器，通过选取调速系统的一个或多个信号作为输入，对系统进行相位补偿，附加给系统正阻尼力矩，将系统的机电振荡模式在复平面上向左迁移。取-Δω为GPSS的输入信号，传递函数框图如图4所示。

图4中，KGPSS为增益系数，Tf为滤波器时间常数，Tnum.k与Tden.m为超前滞后校正环节时间常数，m、n、k在具体设计中均为常数。

图4 GPSS控制框图

调速系统由控制系统模块和执行机构模块组成，其传递函数用Gcon(s)、Gact(s)表示，配置GPSS的汽轮机侧模型如图5所示。

图5 配置GPSS的汽轮机侧模型

2.2 改进型ALO算法

蚁狮算法由文献[22]提出：蚁狮通过挖掘陷阱捕食蚂蚁，并根据已猎食数量动态调整陷阱位置。ALO运行原理参见图6，其中，RB为适应度取值最优的蚁狮，RA为轮盘赌方式下蚂蚁选择的蚁狮，RE为距蚂蚁最近的蚁狮位置。本节针对ALO遍历多样性较差、迭代后期蚁狮移动步长较大等问题，对适应因子I及蚁狮开发方式进行改进。

(Ⅰ)适应因子I改进

当蚂蚁走进蚁狮的陷阱中，其随机行走的超球面半径在适应因子I的影响下逐渐变小。ct和dt是第t次迭代中所有变量的最小和最大取值，约束为：

(14)

其中：I=10w·(t/T)，其中T为最大迭代次数，w为收缩因子，w取值为

(15)

该约束下的I呈分段线性特性，且在第t次迭代中，蚁群游走的超球面半径相同，将I改进为：

(16)

其中：Rrand是在区间[0,1]产生的均匀分布随机数，式(16)中引入三角函数项，随着迭代进行，该项在(0,1)随机非线性递增，适应因子I值呈现具有随机性的非线性自适应递增，蚁群游走的多样性增强，全局搜索能力得到提升。

(Ⅱ)蚁狮开发方式改进

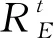
(17)

2.3 目标函数设计

机电振荡模式λs=ζs±jωs中，实部ζs与虚部ωs对系统动态表现均有影响。机电模式阻尼比定义为：

(18)

阻尼比ξs作为基于系统机电振荡特征值的二次性能变量，是低频振荡发生时表征系统振荡衰减速度和振荡角频率的综合指标。在模态识别得到的系统特征根中包含不同的振荡模式，频率为0.1～2.5 Hz的模式属于低频振荡模态[23]。设计目标函数时，为使系统阻尼保持在一定水平之上，对低频振荡模态最小阻尼比加以约束，定义最小阻尼比ξmin=min{ξ1,ξ2,…,ξs}。以ξmin的最大化作为GPSS参数优化的目标函数。

GPSS的结构如图2所示，令n=2，此时GPSS传递函数为：

(19)

结合GPSS参数取值范围约束，优化条件表示为：

(20)

根据GPSS控制器各环节典型参数取值范围，取Tf=5，T1=0.05，T3=0.05。约束KGPSS的取值为[0.01,50.00]，约束T2和T4的取值为[0.01,1.00]。

2.4 改进型ALO优化GPSS参数流程

本文将改进ALO应用于GPSS的参数优化设计中，对含有汽轮机侧附加阻尼控制的发电机组进行仿真，安装于调速侧的GPSS对应3个待求变量，即增益KGPSS、时间常数T2和T4。在此三维寻优的迭代过程中，设优化变量向量为：Xk={KGPSS.k,T2.k,T4.k}，每一个蚁狮个体对应一个优化变量向量解，在系统的低频振荡曲线中运用模态辨识方法提取振荡模式特征值，以基于特征值的二次性能阻尼比目标函数J的取值指导蚁狮种群寻优方向，通过不断的迭代更新搜索最优的GPSS配置参数，基于改进ALO的GPSS优化配置过程的基本步骤如下：

(Ⅰ)初始化改进ALO参数，根据蚂蚁和蚁狮种群设定规模，随机产生1组GPSS种群初始解：X={X1,X2,…,Xs}。

(Ⅱ)对汽轮机组及发电机组参数进行配置，并将其接入无穷大系统，在仿真模型中，对励磁系统额定电压输入端施加5%阶跃扰动，系统产生低频振荡响应。

(Ⅲ)选取与低频振荡密切相关的状态变量Δω，采集其低频振荡响应曲线数据，针对每一个蚁狮搜索个体，采用Prony算法[24]对各机电模式进行模态识别，求取系统各机电振荡模式特征值，进而求取各机电振荡模式阻尼比。

(Ⅳ)评估基于特征值的最小阻尼比性能函数J，该值为系统各机电振荡模式间相互比较寻求所得的最劣阻尼比中的最大值。

(Ⅴ)利用改进ALO的随机游走、构造陷阱和捕食猎物等操作算子进行寻优操作，更新获得下一代候选解X。

(Ⅵ)回到步骤(Ⅱ)进入下一循环，直至达到最大迭代次数，循环终止。

(Ⅶ)输出最优GPSS配置参数及相应的目标函数J。

基于改进ALO的GPSS配置方案如图6所示。GPSS参数寻优的最终目的是获得满足系统动态稳定性要求的配置方案，使得系统发生低频振荡时，可从汽轮机调速侧对振荡进行快速抑制。

图6 基于改进ALO的GPSS优化配置策略

3 算例分析

3.1 优化结果

本节通过对某火电厂汽轮机组构成的单机无穷大系统搭建仿真模型，并通过改进型ALO对GPSS进行优化设计。

励磁系统PSS优化设计Simulink软件仿真研究中，将发电机的输入Pm(机械功率)设置为工况运行时的常数，即忽略原动机侧的动态响应。本文在模型搭建过程中，以美国电气与电子工程师协会单机无穷大模型[20]为基础，发电机额定容量为200 MVA，设定火电机组向电网输送的功率为火电机组75%额定功率。在发电机输入端口连接汽轮机侧模块，并按照2.1节所述，在汽轮机调速系统安装GPSS，仿真汽轮机侧在系统暂态中的表现。汽轮机模型和调速系统模型如图7和图8所示。

图7 汽轮机模型

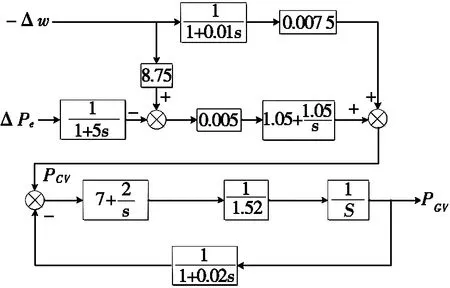
图8 调速系统模型

设置蚂蚁和蚁狮种群规模均为60、维数为3、最大迭代次数为200的改进型ALO，对KGPSS、T2和T4进行优化，且与相同设置条件下的常规ALO寻优结果进行比较。KGPSS、T2和T4的优化结果见表2。

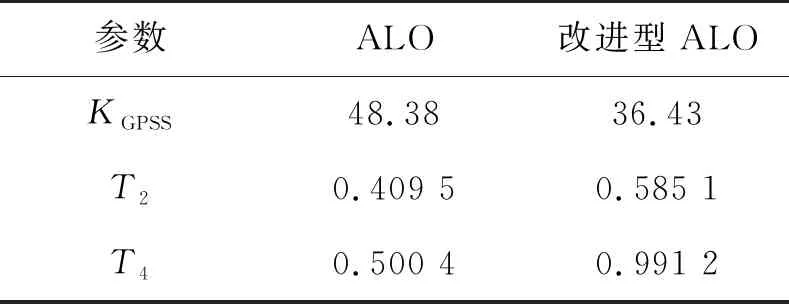
表2 参数优化结果

最小阻尼比及其特征值见表3。如表3所示，未加装GPSS参数时，系统振荡模式中的最小阻尼比为0.050，系统处于弱阻尼状态。安装常规ALO优化的GPSS后系统整体阻尼增强，最小阻尼比为0.172，系统阻尼特性已得到提升。改进型ALO将系统最小阻尼比提高至0.249，阻尼特性进一步改善，这也表明改进型ALO的寻优特性更强。

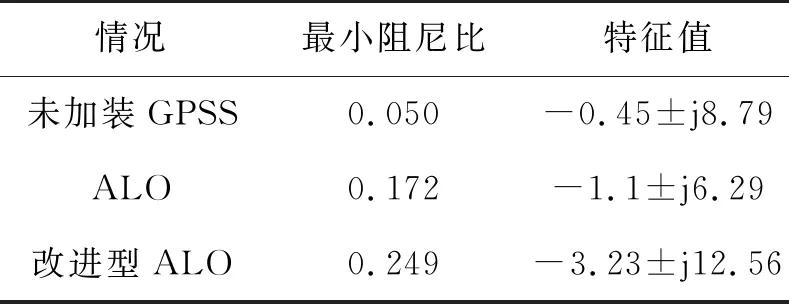
表3 最小阻尼比及其特征值

3.2 GPSS振荡抑制效果仿真

对比不同扰动下3种优化方法的响应特性。未加装GPSS时，振荡波形标记为NO-GPSS；常规ALO整定的GPSS振荡波形记录为ROU-GPSS；改进型ALO整定的GPSS振荡波形记录为OPT-GPSS。

3.2.1 小扰动情况下的GPSS性能分析

在发电机励磁系统输入参考电压中加5%阶跃扰动，扰动持续时间为0.2 s。转子角偏差Δδ与转子角速度偏差Δω均是与低频振荡密切相关的状态变量，其响应曲线分别如图9和图10所示。

图9 转子角偏差动态响应曲线

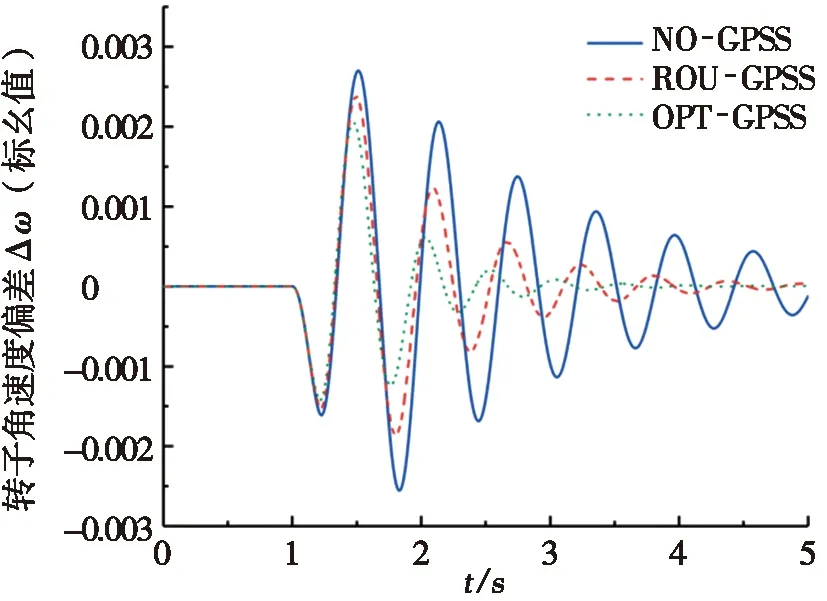
图10 小扰动情况下转子角速度偏差动态响应曲线

图9中，采用ROU-GPSS整定的GPSS对转子角偏差Δδ的低频振荡已能形成有效收敛，而OPT-GPSS算法优化的GPSS，转子角速度摆动幅度最小，Δδ达到稳定的时间也最短。

图10为转子角速度偏差Δω(标幺值)的响应曲线。未安装GPSS时，Δω的响应振幅大，状态变量在长时间内处于波动状态。采用OPT-GPSS优化设计的振荡控制器，Δω响应的波动振幅最小，Δω动态响应在4.5 s时即达到稳定。

3.2.2 大扰动情况下的GPSS性能分析

在输电线路中设置t=0.5 s发生三相接地短路故障，持续时间为0.1 s。此时Δω(标幺值)的响应曲线如图11所示。

从图11中可知：未装设GPSS的电力系统，在遭遇大扰到时，电力系统发生低频振荡，且Δω的响应幅值波动大，其响应在8.6 s时才趋于稳定，系统阻尼性能弱。将采用ROU-GPSS以及OPT-GPSS优化整定后的GPSS装设到电力系统中，此时Δω的波动幅度明显减小，且OPT-GPSS优化整定的GPSS表现出的稳定性更优，Δω波动在2.9 s时便趋于稳定。GPSS作为安装在汽轮机侧的振荡控制器，在系统的暂态稳定状态也具有良好的阻尼特性。

图11 大扰动情况下转子角速度偏差动态响应曲线

3.2.3 多工况鲁棒性校验

在采用OPT-GPSS获得的GPSS配置方案下，将系统从原75%额定工况分别调整至25%、50%和90%，对系统多工况下动态稳定的鲁棒性进行校验，以参考电压5%阶跃扰动下的转子角偏差响应作为考核指标，多工况下的Δδ响应曲线如图12所示。由图12可知：Δδ的初始稳态值随运行工况的不同而发生改变，且随着系统工况增加，系统低频振荡响应幅值呈现扩大趋势，运行工况与振荡剧烈程度具有正相关性。在安装GPSS后，系统多工况下的振荡曲线均能在4.2 s内平息，且在低工况下GPSS的抑制效果更优，25%额定工况下的Δδ响应在3.1 s便快速收敛，配置方案在变工况系统中具有良好的鲁棒性能。

图12 多工况下转子角偏差动态响应曲线

4 结论

(1)通过建立机网耦合模型,考虑汽轮机作为原动机时机械功率的动态变化，采用状态空间和传递函数模型，分析汽轮机侧对电力系统阻尼性质的影响，汽轮机侧参数的不合理配置是导致电力系统低频振荡的关键因素之一。

(2)通过引入三角函数项和反调因子，对ALO算法进行改进，使用改进型ALO算法对GPSS中的超前环节参数配置设计，通过提升振荡模态中的最小阻尼比，保证优化设计后的GPSS，使系统具有更优的动态响应速度以及阻尼性能，且在多工况下具有良好的鲁棒性。