基于双决策和快速分层的多目标粒子群算法
王世华, 李娜娜, 刘衍民
(1.贵州大学 数学与统计学院,贵阳 550025;2.贵州民族大学 数据科学与信息工程学院,贵阳 550025;3.遵义师范学院 数学学院, 贵州 遵义 563006)
0 引 言
自然科学和社会科学等多个领域中的优化问题几乎都是多目标优化问题(MOPs)[1]。由于多目标优化问题中任何两个目标或者多个目标之间是相互制约的,所以它的求解方法与单目标优化问题的求解策略不同。通常是利用传统的加权、混合等方法将多目标优化问题进行转化,然后采用单目标优化问题中比较成熟的求解方法对转化后的多目标优化问题进行求解。但是,随着多目标优化问题中待优化目标的不断增多,传统的优化方法不再适用于解决这类复杂的优化问题,因此,学者们提出启发式算法来解决一些比较复杂的多目标优化问题。粒子群算法(PSO)[2]是一种经典的基于种群的启发式算法,因其具有收敛速度快和易于实现等特点,在单目标优化问题中得到了广泛应用。一些研究表明,改进的PSO适合求解MOPs,如Coello等[3]提出的多目标粒子群算法(MOPSO),该算法采用外部存档对迭代产生的非劣解进行存储,并选择这些非劣解来引导其他粒子飞行。MOPSO为PSO求解多目标优化问题提供了思路和方法,但由于MOPSO在求解一些含有多个目标的优化问题时容易陷入局部最优并且多样性差,许多学者对其进行了改进[4-7]。Li等[4]将粒子的排序优势和切比雪夫距离集成到MOPSO中,增加最优粒子的选择限制,促使粒子向真实的Pareto前沿移动,增强了算法的收敛性,但该方法在解决多峰问题时并没有表现出较大优势;Mostaghim等[5]采用sigma法来选取全局最优粒子,该方法的使用虽然提升了种群的多样性,但是选出的粒子通常分布在非劣解比较集中的区域,在求解一些多目标优化问题时容易陷入局部最优;Li等[6]利用目标函数加权法自适应地选取全局最优粒子,并采用变异来防止算法陷入局部最优,有效地提升了算法的收敛性和多样性,但在解决高维目标问题上还有一定的不足;Leng等[7]利用网格距离法对外部存档的维护策略和全局最优粒子的选取方式进行改进,使得算法的收敛性和多样性有了一定程度的提升,但增加了计算的复杂度。
上述各种策略从种群的多样性和非劣解的收敛性等方面对MOPSO进行改进和优化,虽然取得了较好的研究成果,但是这些策略只对MOPSO的某一性能进行了改进,在其他性能指标上并没有表现出较大的优势。例如文献[5]中,多样性方面得到了很大程度的提升,但是其收敛性方面还存在很大的不足。因此,本文提出一种基于双决策和快速分层的多目标粒子群算法(DDFSMOPSO)来进一步提升种群的多样性和非劣解的收敛性。DDFSMOPSO算法加入了拥挤距离和绝对距离,对MOPSO的外部存档规模的维护策略进行了改进,有效地提升了种群的多样性;与此同时,对全局学习样本的选取方式进行了优化,提出了快速分层策略,增强了非劣解的收敛性。
1 相关概念
1.1 多目标优化问题
有n个决策变量,m个目标的多目标优化问题表示如下:
其中,x=(x1,x2,…,xn)∈X⊂Rn为n维决策变量;y=(y1,y2,…,ym)∈Y⊂Rm为m维目标变量;gi(x)≥0(i=1,2,…,p)和hj(x)=0(j=1,2,…,q)为约束条件。
1.2 粒子群算法
粒子群算法(PSO)是通过选择适当的粒子来引导种群对优化空间进行搜索,从而获得最优解的一种启发式优化算法,因其概念简单、易于实现等特点,在诸多领域得到了广泛应用。由于PSO在求解各领域的单目标优化问题时取得了良好的效果,基于此,学者们将PSO拓展到多目标优化领域,提出了基于外部存档思想和Pareto占优原理的多目标粒子群算法(MOPSO)。在每次迭代过程中,不论是单目标粒子群算法(PSO)还是多目标粒子群算法(MOPSO),粒子i都遵循式(1)和式(2)来更新其速度和位置。
vi(t+1)=w.vi(t)+c1.r1(pi(t)-xi(t))+
c2.r2(g(t)-xi(t))
(1)
xi(t+1)=xi(t)+vi(t+1)
(2)
其中,c1,c2为学习因子;r1,r2为[0,1]区间上的随机数;w为惯性权重;pi(t)为粒子的个体学习样本,它表示在迭代的t时刻,粒子i所经历过的最优位置;g(t)为粒子的全局学习样本,它表示在迭代的t时刻种群中最优粒子的位置。
2 基于双决策和快速分层的改进算法(DDFSMOPSO)介绍
2.1 外部存档的维护
多目标粒子群算法一般采用外部存档对每一次迭代产生的非劣解进行存储,随着迭代的进行,外部存档中的非劣解逐渐增多,当外部存档规模超出预设的最大规模时,将超出规模的那一部分粒子进行有效删除,不但可以提高算法的搜索能力,而且还能维护种群的多样性。因此,这里采用拥挤距离(Crowding Distance,CD)和绝对距离(Absolute Distance,AD)相结合的双决策(Double Decision,DD)策略来维护外部存档规模。本文将粒子与其相邻粒子欧式距离之和作为其拥挤距离,将粒子与其相邻粒子的欧氏距离之差的绝对值作为其绝对距离,式(3)和式(4)给出了拥挤距离和绝对距离的计算公式。
(3)
DA(Xi)=|d(Xi,Xi-1)-d(Xi,Xi+1)|
(4)
其中:n为外部存档中粒子的数量;d(Xi,Xi-1)为粒子Xi到粒子Xi-1的欧式距离;d(Xi,Xi+1)为粒子Xi到粒子Xi+1的欧式距离;DC(Xi)为粒子Xi的拥挤距离;DA(Xi)为粒子Xi的绝对距离。
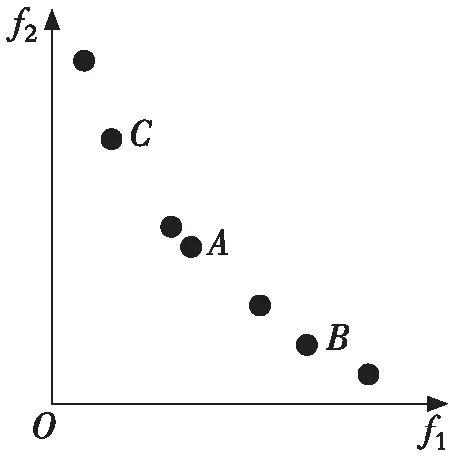
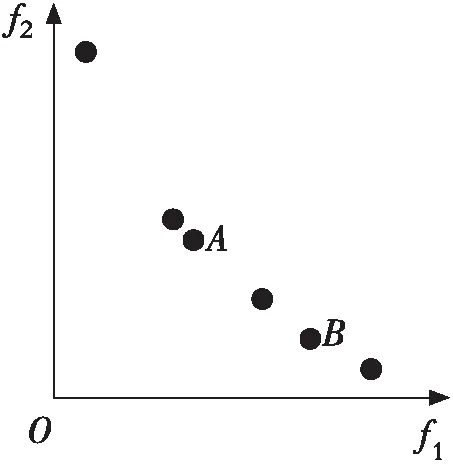
随着迭代的进行,当外部存档规模超出预设的最大规模时,双决策策略被启用。其具体流程如下:首先根据式(3)计算外部存档中所有粒子的拥挤距离,然后根据拥挤距离的值从小到大删除超出存档规模的那部分粒子,若存在b(b>1)个粒子的拥挤距离相等,则运用式(4)计算这些粒子的绝对距离,并将绝对距离最大的粒子进行删除。相比于文献[3]用到的随机法、文献[8]用到的拥挤距离法,双决策策略的优点是可以使外部存档中粒子的分布更均匀。下面通过一个实例来进行说明,如图1所示,以外部存档中非劣解分布最密集的一块区域为例,图1(a) 中一共有7个粒子,假如要删除其中的一个,图1(b)是采用拥挤距离法删除过程示意图(删除粒子B);图1(c)是采用随机法删除过程示意图(删除粒子C);图1(d)是采用拥挤距离和绝对距离相结合的双决策策略删除过程示意图(删除粒子A)。通过图1(b),1(c)和1(d)的对比,可以直观地看出:采用拥挤距离和绝对距离相结合的双决策策略对外部存档规模进行维护,使得存档中粒子的分布更均匀。
2.2 全局学习样本的选取
在多目标粒子群算法中,全局学习样本的优劣是决定算法是否有效的关键因素,因此,选取一个较优的全局学习样本至关重要。通常采用文献[3]中的轮盘赌策略选取全局学习样本,该策略操作简单,易实现,但不利于保持算法的收敛性。鉴于此,这里采用快速分层(Fast Stratification,FS)策略对全局学习样本进行选取。本文将粒子的标准化目标值作为其快速分层值,于是粒子Xi的快速分层值为
(5)
其中,M为目标个数;fj(Xi)为粒子Xi的第j个目标函数值;fjmin和fjmax分别为第j个目标函数在目标空间中的最小值和最大值;SF(Xi)表示粒子Xi的快速分层值。快速分层策略的具体流程如下:首先运用式(5)计算外部存档中每个粒子的快速分层值,并根据分层值的大小将粒子进行升序分层,第一层为第一等级,第二层为第二等级,依次给出所有粒子的等级,然后从第一等级的粒子中随机选择一个作为全局学习样本。如图2所示,以二维目标空间中的3个粒子为例,图2中给出了将粒子进行快速分层后的示意图,从图2中可以看出,第一等级的粒子距离真实的Pareto前沿(PF)较近。选择第一等级的粒子作为全局学习样本来引导飞行,可以提升粒子向真实的Pareto前沿飞行的概率,进而提升算法的收敛性。
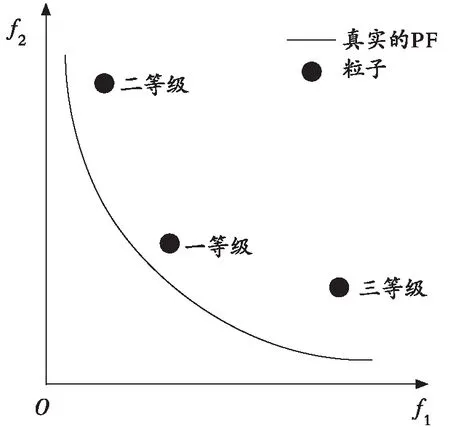
图2 全局学习样本的选取示意图Fig. 2 Schematic diagram of global learning sample selection
2.3 算法流程
图3为DDFSMOPSO算法的流程图。
具体步骤如下:
① 设置DDFSMOPSO算法的相关参数,初始化种群;
② 对粒子位置进行变异操作,并计算其适应度值;
③ 对于每个粒子,将当前迭代的适应度值与该粒子的历史最优适应度值进行比较,优者即被选为个体学习样本(pbest),若相等,则随机选择一个;
④ 建立外部存档,然后利用拥挤距离和绝对距离相结合的双决策策略对其规模进行控制,并将存档中的粒子予以更新;
⑤ 利用快速分层策略在外部存档中选择一个粒子作为全局学习样本(gbest)引导飞行;
⑥ 运用式(1)和式(2)更新每个粒子的位置和速度;
⑦ 判断是否满足终止条件,若满足则迭代结束,否则返回第②步。
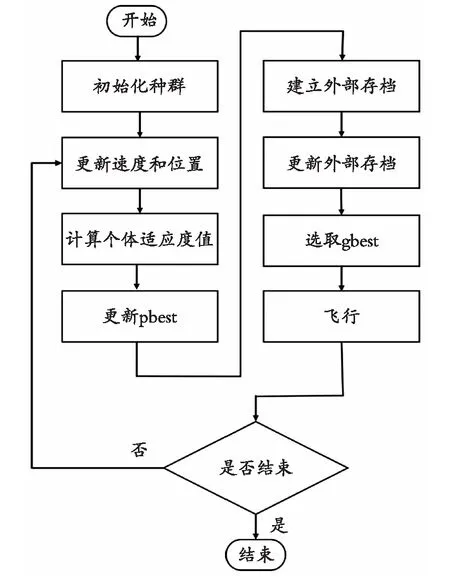
图3 DDFSMOPSO算法流程图Fig. 3 Flow chart of DDFSMOPSO algorithm
3 实验结果与分析
3.1 评价指标
本文采用收敛性指标(GD)[9]度量算法所获得的非劣解与真实的Pareto前沿的逼近程度,GD值越小意味着非劣解越接近真实的Pareto前沿,即算法的收敛性越好;采用分布性指标(Δ)[10]度量算法所获得的非劣解的分布情况,Δ值越小意味着非劣解的分布越均匀,多样性也就越好;采用标准化空间指标(IH)[11]度量算法所获非劣解覆盖真实的Pareto前沿与参考点RP所包围空间的比率,IH值越大意味着算法的综合性能越好。由于篇幅所限,3种评价指标的表达式请参阅文献[9-11]。
3.2 实验条件及参数设置
为了更好地验证DDFSMOPSO算法的性能,选取4个二维测试函数(ZDT1,ZDT2,ZDT3,ZDT4)[12]和两个三维测试函数(DTLZ1,DTLZ2)[13]对4种算法(DDFSMOPSO,NSPSO[14],MOPSO[3],SMOPSO[5])进行测试。DDFSMOPSO算法的参数设置如下:种群规模为200,外部存档规模为200,迭代次数为 2 000,其他算法的参数与各种算法提出时保持一致。
3.3 算法的仿真结果分析
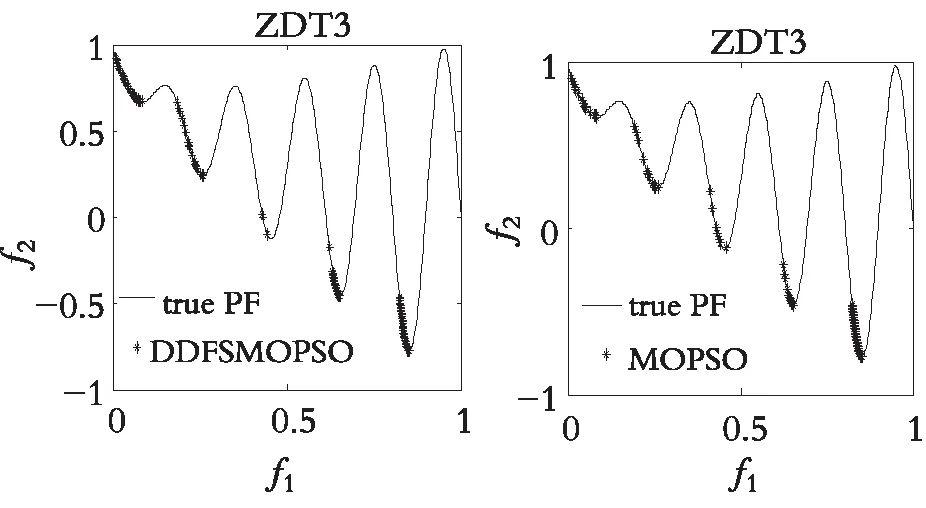
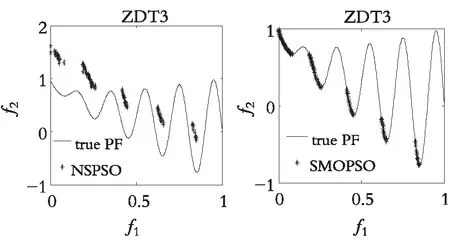
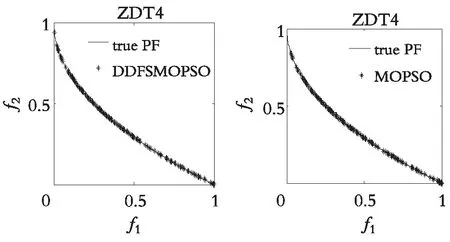
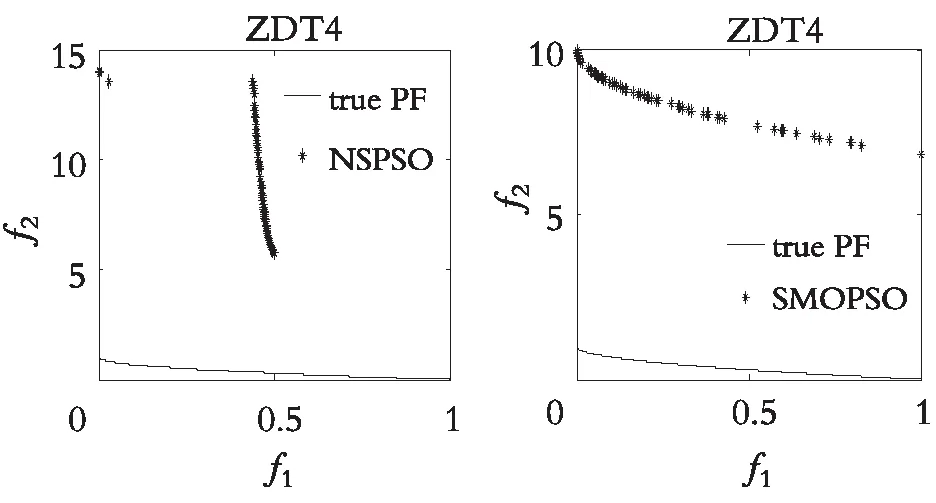
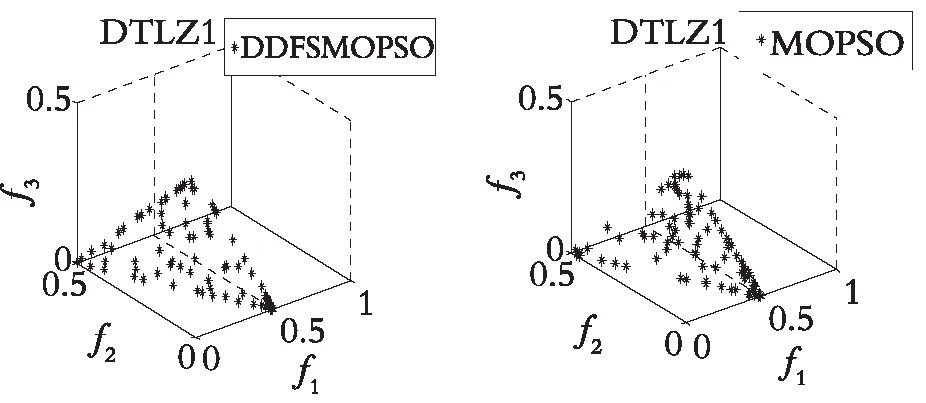
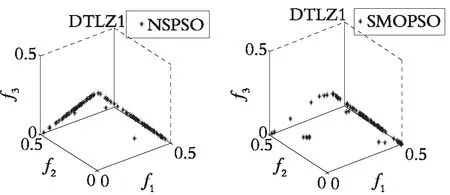
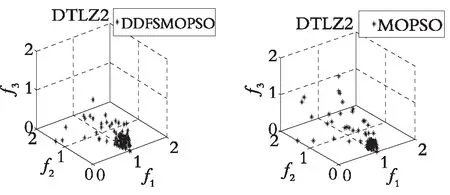
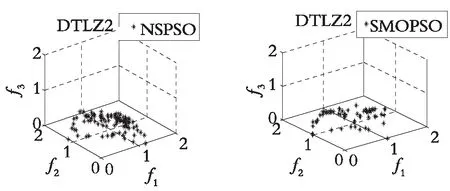
图4—图7分别展示了DDFSMOPSO,MOPSO,NSPS0和SMOPSO 4种算法在二维测试函数ZDT1,ZDT2,ZDT3,ZDT4上的仿真结果图。图8—图9分别展示了DDFSMOPSO,MOPSO,NSPS0和SMOPSO 4种算法在三维测试函数DTLZ1,DTLZ2上的仿真结果图。
从图4—图7可以得出:在测试函数ZDT1和ZDT2上,DDFSMOPSO算法所获得的非劣解的收敛性明显好于算法NSPSO和SMOPSO;在测试函数ZDT3上,DDFSMOPSO,MOPSO和SMOPSO 3种算法所获得的非劣解都能收敛到真实的Pareto前沿,并且DDFSMOPSO算法所获得的非劣解的分布性明显优于MOPSO算法,算法NSPSO所获得的非劣解与真实的Pareto前沿还有一定的距离;值得注意的是,在测试函数ZDT4上,DDFSMOPSO算法所获得的非劣解几乎能覆盖整个Pareto前沿,无论是解的分布性还是收敛性,DDFSMOPSO算法都要好于算法MOPSO,NSPSO,SMOPSO。从图8—图9可以得出:在测试函数DTLZ1上,DDFSMOPSO算法所获得的非劣解的分布性明显优于算法MOPSO,NSPSO和SMOPSO;在测试函数DTLZ2上,DDFSMOPSO算法所获得的非劣解的分布性优于MOPSO算法,略差于算法NSPSO和SMOPSO。综上所述,相比于算法MOPSO,NSPS0和SMOPSO,DDFSMOPSO算法在解的分布性和收敛性上都表现出较大的优势。
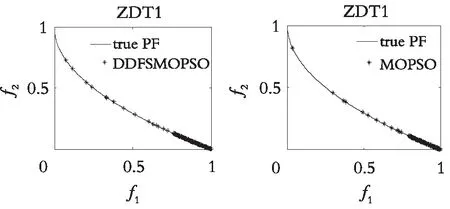
(a) DDFSMOPSO (b) MOPS0
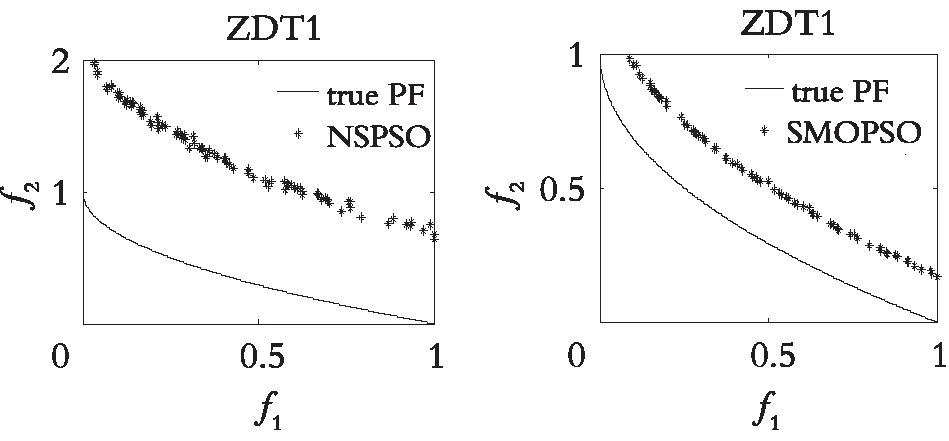
(c) NSPSO (d) SMOPS0
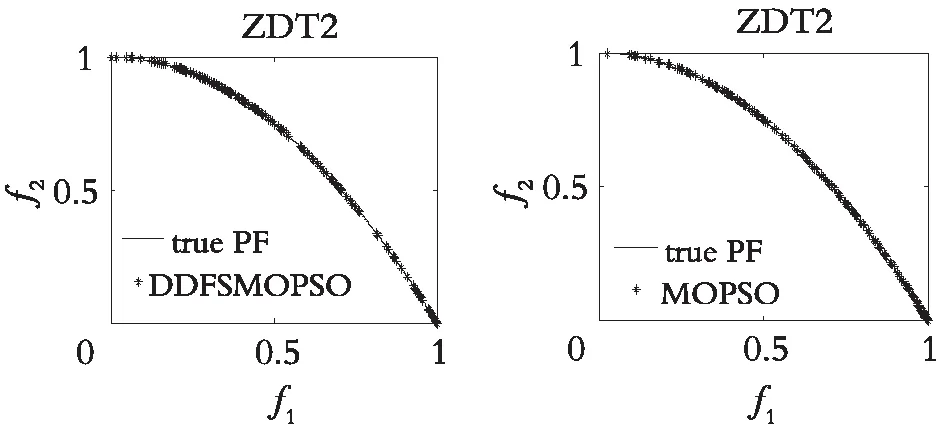
(a) DDFSMOPSO (b) MOPS0
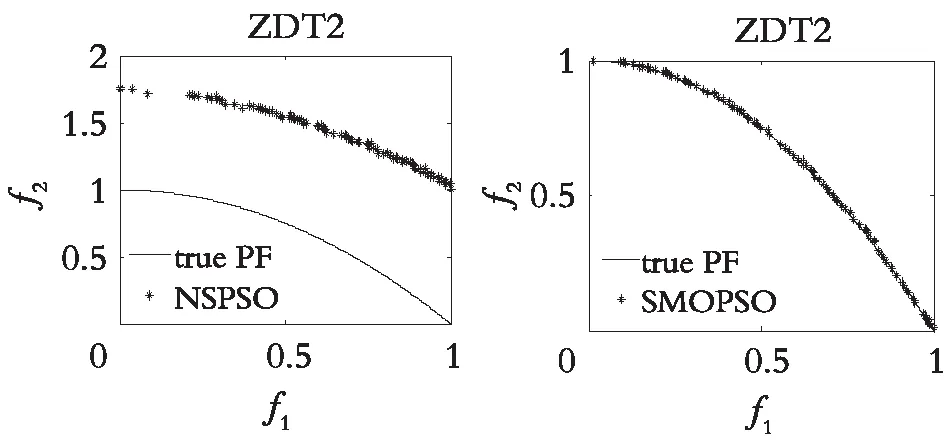
(c) NSPSO (d) SMOPS0
(a) DDFSMOPSO (b) MOPS0
(c) NSPSO (d) SMOPS0
(a) DDFSMOPSO (b) MOPS0
(c) NSPSO (d) SMOPS0
(a) DDFSMOPSO (b) MOPS0
(c) NSPSO (d) SMOPS0
(a) DDFSMOPSO (b) MOPS0
(c) NSPSO (d) SMOPS0
3.4 算法的收敛性和多样性分析
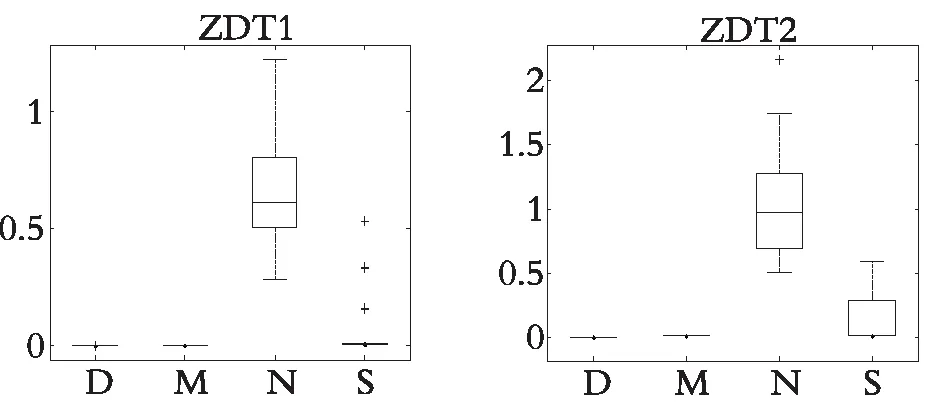
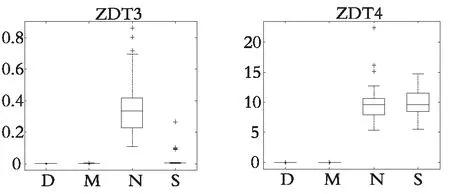
表1和表2分别展示了DDFSMOPSO,MOPSO,NSPSO和SMOPSO 4种算法在测试函数ZDT1,ZDT2,ZDT3和ZDT4上运行30次所获得的收敛性指标(GD)和分布性指标(Δ)的最大值、最小值、平均值和标准差,图10和图11分别展示了各种算法运行30次所获得的GD值和Δ值的盒状统计图(横坐标,D表示DDFSMOPSO算法;M表示MOPSO算法;N表示NSPSO算法;S表示SMOPSO算法)。下面将根据各种算法所获得的GD指标和Δ指标,对算法的收敛性和多样性进行分析。

表1 各种算法在测试函数ZDT1-ZDT4上的GD指标Table 1 GD index of various algorithms on test functions ZDT1-ZDT4

表2 各种算法在测试函数ZDT1-ZDT4上的Δ指标Table 2 Δ index of various algorithms on test functions ZDT1-ZDT4
(a) DDFSMOPSO (b) MOPS0
(c) NSPSO (d) SMOPS0
(a) DDFSMOPSO (b) MOPS0

(c) NSPSO (d) SMOPS0
从表1可以看出:在测试函数ZDT1—ZDT4上,DDFSMOPSO算法获得了比其他3种算法更优的GD值,说明DDFSMOPSO算法的收敛性要优于算法MOPSO,NSPSO和SMOPSO。从图10可以看出,在测试函数ZDT1,ZDT2,ZDT3和ZDT4上,DDFSMOPSO算法所获得的GD值的平均值比算法MOPSO,NSPSO和SMOPSO更接近于零,这与表1的分析结果一致,进一步说明DDFSMOPSO算法具有较强的收敛性。
从表2可以看出:在大多数测试函数上,DDFSMOPSO算法所获得的Δ值明显好于MOPSO算法,略差于NSPSO和SMOPSO算法,这意味着DDFSMOPSO算法的多样性好于MOPSO算法,相比于算法NSPSO和SMOPSO,DDFSMOPSO算法的多样性还有提升的空间。从图11可以看出,在测试函数ZDT2,ZDT3和ZDT4上,DDFSMOPSO算法所获得的Δ值的平均值比MOPSO算法更接近于零,这与表2的分析结果一致。
3.5 算法的综合性分析
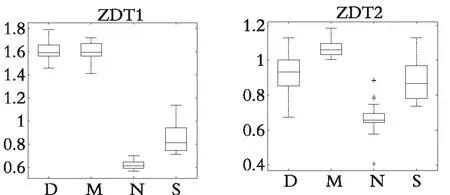
表3展示了DDFSMOPSO,MOPSO,NSPSO和SMOPSO 4种算法在三维测试函数DTLZ1和DTLZ2上运行30次所获得的IH指标的最大值、最小值、平均值和标准差,图12展示了各种算法运行30次所获得的IH值的盒状统计图(横坐标D表示DDFSMOPSO算法;M表示MOPSO算法;N表示NSPSO算法;S表示SMOPSO算法)。
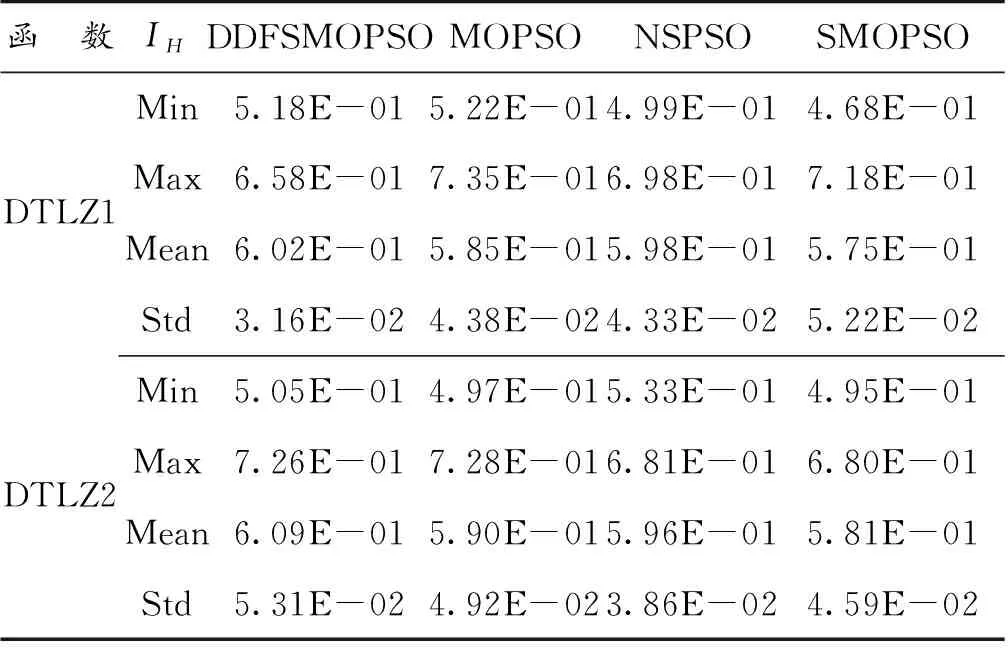
表3 各种算法在测试函数DTLZ1-DTLZ2上的IH指标Table 3 IH index of various algorithms on test functions DTLZ1-DTLZ2
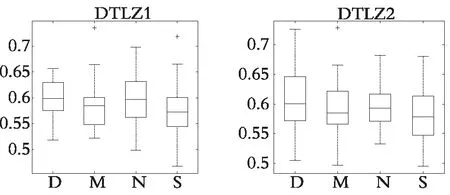
图12 IH值的盒状统计图Fig. 12 Box chart of IHvalues
从表3可以看出,在测试函数DTLZ1和DTLZ2上,DDFSMOPSO算法所获得的IH值明显优于算法MOPSO,NSPSO和SMOPSO,说明DDFSMOPSO算法有较好的综合性能。从图12可以看出,在测试函数DTLZ1和DTLZ2上,DDFSMOPSO算法所获得的IH值的平均值都大于算法MOPSO,NSPSO和SMOPSO,说明DDFSMOPSO算法的综合性能好于与之相比的3种算法。
4 结束语
为了提升种群的多样性和收敛性,本文提出了基于双决策和快速分层的多目标粒子群算法(DDFSMOPSO)。该算法采用拥挤距离和绝对距离相结合的双决策策略对外部存档规模进行维护,使得优秀粒子在随后的进化过程中易于保留和发展,有效地提升了种群的多样性。同时,为提升粒子收敛到真实Pareto前沿的概率,采用快速分层策略对全局学习样本进行选取。将DDFSMOPSO算法与MOPSO,NSPSO和SMOPSO 3种算法在同一环境下进行仿真实验,实验结果表明:与其他3种算法相比,DDFSMOPSO算法在多样性、收敛性以及综合性能上均有明显改善,这意味着DDFSMOPSO可以作为求解多目标优化问题的有效算法。

