基于投影空间下奇异值分解的海面小目标CFAR检测

时艳玲, 王 磊, 李君豪

(南京邮电大学通信与信息工程学院, 江苏 南京 210003)

0 引 言

海杂波是指雷达发射的电磁波照射到海洋表面后的后向散射回波,这种杂波信号容易受到海面风速、温度、浪高等各种海洋环境因素和雷达的频率、擦地角、极化方式等设备因素的影响,具有非均匀、非高斯、非平稳等复杂的统计特性和物理特性[1-2]。同时,海面目标回波信号无论是在时域还是在频域都会受到海杂波信号和其他信号的影响。因此,在海杂波背景下检测小目标便成为雷达领域中十分具有挑战性的问题[3-6]。

为了改善雷达的检测性能,一般采用增强信杂比(signal to clutter ratio,SCR)[7-8]和抑制杂波[9-11]这两种方式。由于海面小目标回波信号弱,常规雷达中难以获得高信杂比,在低信杂比情况下,传统的自适应检测方法难以获得理想的检测性能。于是,很多学者考虑通过杂波抑制的方法提高信杂比,较为传统的杂波抑制方法有基于频域滤波器的脉冲对消法[12-13],该方法利用目标和海杂波在频率上的差别抵消零频杂波,但由于海况的不稳定性，容易导致海杂波中心频率偏移零频,导致抑制效果不理想,不利于目标的检测。因此,Sanzgonzalez等将奇异值分解的方法用于海杂波的抑制[14],但是当海杂波Bragg峰不明显的时候,抑制效果会变差。Yasotharan等提出了一种时频滤波的杂波抑制方法[15-16],该方法能够自适应地进行时频滤波,滤除杂波信号的同时还能减少目标信号的损失。Salvatore等根据海杂波的时变特性,提出了一种线性预测的方法[17],通过延长回波数据的长度提高多普勒频率,实现杂波和目标的分离,但是线性预测的模型参数难以选择,影响检测性能。基于子空间的思想,Yang等提出了一种基于正交投影的恒虚警率(orthogonal projection constant false alarm rate, OP-CFAR)检测算法[18-19],该方法考虑了雷达回波信号邻近距离单元的相关性,在投影空间上构造一个正交投影算子抑制杂波,降低了计算复杂度,但是当存在干扰信号时,目标的检测效果不理想。还有学者通过研究海杂波的分数阶傅里叶变换(fractional Fourier transform, FRFT)谱特性改善雷达的检测性能[20-21]。

由此,基于子空间的思想,针对文献[18]中的OP-CFAR检测器检测性能不理想和抗干扰性能差的情况,提出了一种基于投影空间下奇异值分解(singular value decomposition, SVD)抑制方法。该方法首先是利用接收回波中的参考单元样本构造杂波空间,并使用正交投影的原理计算抑制杂波的正交投影算子,实现杂波的第一次抑制,然后对投影算子进行奇异值分解,在信号子空间中设计一个双重抑制杂波的算子,实现杂波的二次抑制。最后,将该杂波抑制算子与恒虚警检测器结合,称为正交奇异值分解恒虚警器(OP-SVD-CFAR)检测。为了验证本文提出的OP-SVD-CFAR检测器的性能,利用实测海杂波数据和仿真目标进行实验,并将OP-CFAR检测器[18-19]、最大特征值的矩阵CFAR(matrix CFAR detection method based on the maximum eigenvalue, MEMD)检测器[22]、分数阶域奇异值分解(SVD-FRFT)检测器[23-24]以及单元平均恒虚警(cell average constant false alarm rate, CA-CFAR)检测器这4种方法作为对比[25],实验结果证明本文所提的检测器性能更优。

1 基于投影空间下奇异值分解的杂波抑制方法

雷达所接收到的待检测单元回波信号可以表示为下式所示的二元假设检验问题:

(1)

式中:H0是零假设,表示无目标；H1是备则假设,表示有目标；x=[x(1),x(2),…,x(N)]T为观测到的信号；s=[s(1),s(2),…,s(N)]T为目标信号；c=[c(1),c(2),…,c(N)]T为海杂波信号；g=[g(1),g(2),…,g(N)]T为干扰信号；N为平均执行周期时间内的脉冲数；[·]T表示转置运算。

在雷达回波数据中有若干个距离单元,选取其中L个距离单元作为参考单元。将第l个距离单元的参考样本设定为xl=[xl(1),xl(2),…,xl(N)]T(l=1,2,…,L),参考样本为不含目标信息的回波信号,位于待检测单元周围,即除待检测单元左右邻近的单元之外的距离单元。由此可获得L个参考样本,将其进行排列,有X=[x1x2…xL],即构建为参考样本的向量子空间,如图1中的平面A。

(2)

由于雷达数据中各距离单元回波信号之间存在一定的相关性,所以待测单元的杂波信号可以通过其他邻近距离单元的杂波信号表示,其表达式为

(3)

(4)

式中：[·]H表示共轭转置;φx是在子空间X上的投影算子。根据式(2)和式(4)可得正交投影抑制后剩余信号可以表示为

(5)

考虑到奇异值分解在杂波抑制方面的广泛应用,即当给定一信号空间,我们可以通过SVD将该信号空间中的杂波分离出来,从而突显所需的目标信号。当在给定信号空间X=[x1x2…xL]的条件下,可将该信号空间的杂波协方差矩阵估计为下式所示:

(6)

式中：S是埃尔米特(Hermitian)矩阵,且S的大小N×N。对矩阵S进行奇异值分解：

S=UΣVH

(7)

式中：U∈RN×N为S的左奇异向量,U的每一列对应的是SSH的正交特征向量;V∈RN×N为S的右奇异向量,V的每一列对应的是SHS的正交特征向量; 同时SSH,SHS的特征值相同,为λ1,λ2,…,λN且λi≥λi+1,λi≥0,于是矩阵S的奇异值可表示为

(8)

(9)

同理Λ为奇异值构成的对角矩阵,R和RH分别为对应的左奇异向量和右奇异向量,将对角矩阵Λ中的前K个较大的奇异值及其对应的奇异向量组成二次杂波算子φxs,因此二次抑制后的剩余信号为

(10)

式中:I为N×N的单位矩阵。

2 基于投影空间下奇异值分解的CFAR检测器

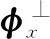
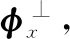
所提方法从本质上看是时域对消法中的动目标显示(moving targets indication, MTI)的一种变型,以检测海面低速小目标为背景,适用于在海杂波主杂波区域以外且径向速度较大的目标检测,具有一定的应用前景。并且该方法在工程上的实现难度较小,只需要加载部分信号处理算法,无需改变系统的硬件设备。下面将对“OP”和“OP+SVD”这2种算法的计算复杂度进行分析,这两种算法的计算量主要取决于正交投影过程和奇异值分解过程,对于一个W阶的矩阵来说,SVD的计算量是O(W3)。而本文中OP的计算复杂度则取决于距离单元的个数L为O(L3),因此在脉冲长度为N的情况下奇异值分解的计算复杂度为O(N3)。由于本文中是正交投影后再对正交投影算子进行一阶奇异值分解,因此,本文算法的计算量为O(L3)+O(N3),通常情况下脉冲长度大于距离单元的个数,因此OP的计算量小于SVD的计算量。当N=L时,本文算法的计算量为O(2N3),这种算法虽然以计算量为代价来换取检测性能,从工程的角度来说,当N较小时,这样的计算量是可以接受的。

3 实验结果和性能分析

3.1 实验数据介绍

采用全相参X波段(ice multiparameter imaging X-band, IPIX)雷达数据库中的10组雷达数据进行实验。该数据集常用于研究海杂波环境中可观测目标的探测[28]。每组数据都由14个距离单元组成,其中,每个距离单元的采样观测时间为131.072 s,即131 072采样脉冲,每组数据的距离分辨率是30 m。

IPIX雷达的主要性能参数如下：射频频率为9.93 GHz;脉冲宽度为200 ns;脉冲重复频率为1 kHz;距离分辨率为30 m;有HH、HV、VH、VV 4种极化方式。实验中选取IPIX雷达数据集中的19931107_135603_starea17(#data1)和19931109_202217_starea31(#data2)这2组数据中的VV和HH极化数据。

3.2 对比算法和实验参数设定

当选定某一个距离单元作为待检测单元时,我们将其邻近的距离单元看作参考单元并以此构造杂波的子空间,假设选取的是第i个单元作为待检测单元,这时就需要选取其邻近的第(i+1)和第(i-1)个单元之外的距离单元构建测试样本的子空间。

为了在不同角度进行对比,本文选取OP-CFAR检测器[18-19]、MEMD检测器[20-22]、SVD-FRFT检测器[23]、CA-CFAR检测器[24]4种检测器进行比较,其中OP-CFAR检测器是利用待检测单元的邻近单元来估计杂波信号,可以将正交投影和CFAR很好的结合到一起,在工程上实现起来较为简单,计算量相对较小,并且具有较好的检测性能;MEMD检测器是一种基于最大特征值的CFAR检测算法,不需要检测先验信息,并且在复杂环境下有较好的检测性能;SVD-FRFT是一种基于分数阶域的单次杂波抑制,利用最优阶傅里叶变换对信号能量的聚集作用,突显出目标信号,分离杂波信号,进而实现抑制杂波,有一定的检测效果;CA-CFAR检测器是均值类CFAR检测器中最为经典的元平均CFAR检测器,通过对局部距离单元功率取平均值的方法来进行检测,以此作为对比的基准。OP-CFAR和SVD-FRFT带有杂波抑制过程,MEMD和CA-CFAR未含杂波的抑制。

在进行检测之前,我们选取#data1中的VV极化数据的第5个距离单元第1 501到第2 500个脉冲数据进行OP算法、SVD-FRFT算法和本文所提的二次抑制算法的抑制效果测试,为了更加直观地看出3种算法的抑制效果,文中通过杂波抑制比的值说明抑制效果,即杂波的抑制量和原始信号能量的比值,结果如图3所示。

从图3中可以看出本文算法的杂波抑制比明显高于对比算法,为了更加客观分析3种算法的性能,在杂波抑制后,3种方法的抑制量分别约为11 dBW、14.1 dBW和33.6 dBW,于是可以得到3种算法的杂波抑制比,其中SVD-FRFT算法为0.477,OP算法为0.586,本文算法为1.361。因此,可以看出本文算法杂波抑制的性能更优。

为了分析本文提出的OP-SVD-CFAR检测器的抗干扰性能,实验过程中分别增加了0 dB和5 dB的干扰信号进行对比分析,将目标信号和干扰信号的多普勒频率分别设为fd=-150 Hz、fd1=-75 Hz,CPI脉冲序列长度N=16,在实验中为了生成足够多的样本数,将每个单元进行滑窗取样,其表达式为

lj=x(d(j-1)+1:d(j-1)+N)

(13)

式中：d=8,是指在相邻向量中调整重叠时间长度的系数；虚警概率Pf为10-3,选取第9个距离单元添加目标信号,对#data1和#data2中VV和HH两个极化数据进行检测。

3.3 检测性能分析

当检测背景中未添加干扰信号时,从图4～图7中可以看出本文提出的OP-SVD-CFAR检测器性能更优。对于#data1 VV极化数据(见图4(a)),当检测概率为0.8时,OP-SVD-CFAR检测器相较于对比算法在检测性能上均有一定程度的提高,相较于OP-CFAR和FRFT-SVD这2种有杂波抑制的算法而言,检测性能改善相对较小，约为2.7 dB和9.5 dB;而相较于MEMD和CA-CFAR算法来说,性能有较大的提升,其改善量约为14 dB和20 dB。对于#data1 HH极化数据(见图5(a)),当检测概率为0.8时,OP-SVD-CFAR检测器相较于4种对比算法的性能改善量分别为3.4 dB、3 dB、13 dB和16 dB。

这是因为OP-SVD-CFAR在构建正交子空间时,通过投影算子φx对杂波第一次抑制,随后在奇异值分解后的信号子空间上实现了杂波的第二次抑制,所以具有最优的检测性能。而OP-CFAR算法只实现了正交子空间上的一次杂波抑制,因此在整体的检测性能上相较于本文的方法有所降低;MEMD算法仅依靠样本间的相关性,没有进行杂波抑制,故其性能受限;SVD-FRFT算法虽然在最优阶情况下实现了信号能量的聚集,但是其前提条件是将海杂波信号假设为线性调频信号,与实际有偏差;CA-CFAR算法作为一种非相干积累算法,性能改善相对有限。

同时,为了验证本文提出的双重抑制算法在抗干扰性上的优越性,在实验中添加了信干比为0 dB和5 dB的干扰信号做对比。当检测概率为0.8时,各算法的性能下降结果如图4和图5所示。通过图中的性能曲线可以看出,当增加了干扰信号后,5种算法的性能均有一定程度下降。具体数据如表1所示。

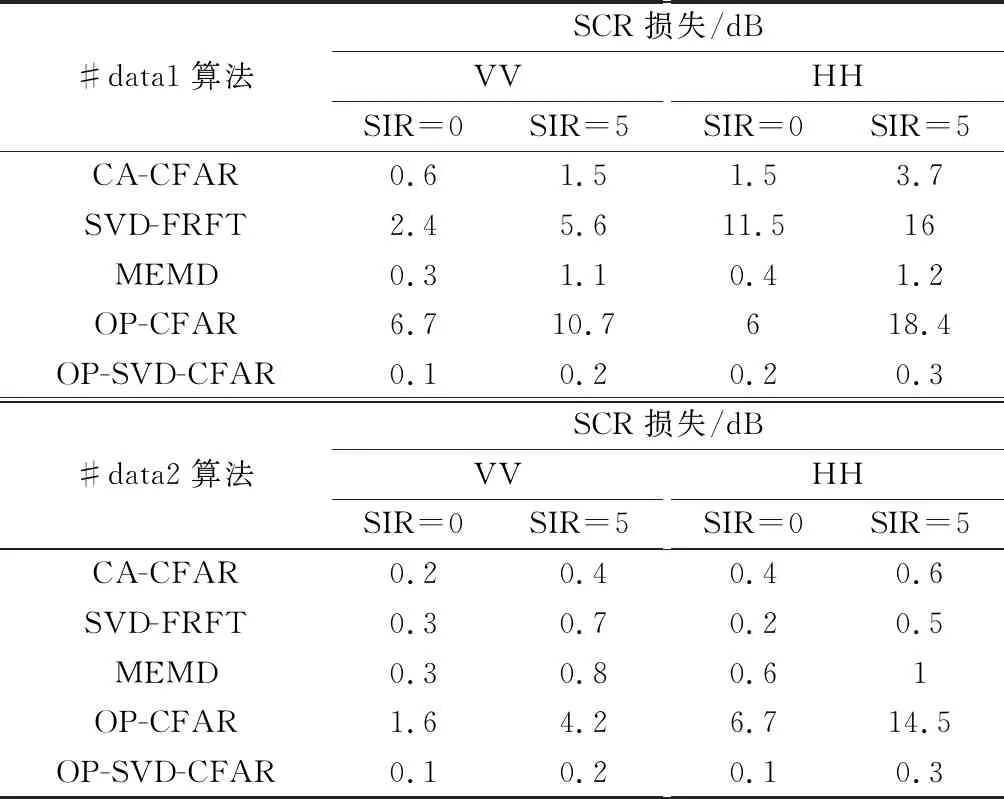
表1 不同SIR下四种算法受干扰影响性能损失

从表1中的数据可以看出,本文提出的OP-SVD-CFAR算法性能损失最小,其平均性能损失小于0.3 dB,对于OP-CFAR和SVD-FRFT检测器,其平均性能损失分别约为8.6 dB和4.6 dB,对于MEMD和CA-CFAR检测器,其平均性能下降约为0.7 dB和1.1 dB,进一步体现了文中提出的OP-SVD-CFAR算法双重抑制的优越性。

通过表1的数据可以看出,5种算法在VV极化上的损失相对小于在HH极化上的性能损失。图8为2组数据在所有距离单元的相关系数,其实验做法为:以第9个距离单元的数据为待检测数据,计算第9个距离单元的数据的自相关系数,计算其他某个距离单元与第9个距离单元数据的互相关系数。

从图8中可以看出,第9个距离单元数据与其他参考单元的互相关系数,在除去第9个距离单元及其左右邻近的距离单元,VV极化的相关系数在总体上是高于HH极化。相关性越高,其由参考单元数据构成的正交子空间更能反映出待检测单元的样本特性,将待检测单元的信号向给子空间投影时,想要的信号信息被保留到该子空间,而存在的杂波被分解到对应的零空间中,实现了保留信号抑制杂波的目的。因此,VV极化在估计和杂波抑制时效果相对更好。

在仿真过程中,统计了正交投影法和本文提出的算法在杂波抑制所用的时间,仿真所用的计算机CPU为Intel(R)Core(TM),内存为2.5 GHz。在Matlab中仿真用时如下:其中使用正交投影法抑制杂波的时间是0.011 s,采用正交投影后奇异值分解法抑制杂波使用的时间是0.805 s。这与第2节中计算复杂度的分析结果相一致,文中提出算法以计算量为代价来换取检测性能,从抑制杂波所用的时间来看,是可以接受的。

4 结 论

本文提出了一种基于投影空间下奇异值分解的方法来抑制海杂波,并将该算法应用于恒虚警检测器,提出了OP-SVD-CFAR检测器,这种检测器将待检测单元的信号投影到由参考单元样本构建的正交子空间上,实现了杂波的第一次抑制,而后将该投影算子进行奇异值分解,在信号子空间上实现了杂波的第二次抑制。虽然本文所提的OP-SVD-CFAR检测器在计算复杂度上有所提高,但是实验结果表明本文所提检测器具有更好的检测性能和抗干扰性能。