基于自适应郊狼算法的无人机离线航迹规划

陈 都, 孟秀云

(北京理工大学宇航学院, 北京 100081)

0 引 言

伴随科技的飞速发展,无人机向着信息化、智能化、体系化方向发展,航迹规划问题作为无人机任务规划的一部分,是无人机自主智能执行任务的一个核心步骤。无人机离线航迹规划是在无人机起飞前,考虑无人机的动力学约束、任务要求、环境因素等,在一个合理的时间内为无人机规划一条从起点到终点的最优航迹。

相对于在线实时的无人机航迹规划,无人机离线航迹规划侧重于规划出飞行轨迹的最优性与稳定性,其本质上是一个多约束多峰高维的最优化问题,因此，元启发式群体智能算法很适合无人机离线航迹规划。元启发式群体智能算法在解决最优化问题时,随机初始化一群个体,每一个个体代表优化问题一个可能的解,在航迹规划问题中每个个体代表一条航迹,然后根据算法的元启发操作算子,更新个体的值,直至达到停止条件。

大量文献对无人机离线航迹规划问题进行了研究,各种元启发式群体智能算法被应用于无人机离线航迹规划,如传统的遗传算法(genetic algorithm,GA)、粒子群优化(particle swarm optimization,PSO)算法、蚁群算法,近些年提出的各种新型算法,如蝙蝠算法、灰狼(grey wolf optimizer,GWO)算法、乌贼算法、共生生物搜索算法、樽海鞘算法等。在用元启发式群体智能算法搜索无人机航迹时,存在两方面问题:一是对于复杂环境的航迹规划问题,算法易陷入局部最优,过早地收敛,全局寻优能力不足,很多文献针对该问题在元启发式算法基础上提出了许多改进策略,如将随机游走、混沌序列、正余弦优化、强化学习等与元启发式算法结合,还有文献将两种基础算法混合,这些改进能在一定程度上提高算法全局搜索能力,但也受限于原始算法本身的特性;二是在建立无人机航迹规划模型时,将问题的维数设置较高时,算法表现不够稳定,有时难以在合理的时间内收敛,针对该问题,许多文献采用降维搜索的策略,如文献[20-21]设置最小威胁曲面搜索,文献[22]通过固定一个方向的数值搜索,还有大多数文献[10,23-24]通过指定较少的航迹点个数或仅在二维平面搜索来降低离线航迹规划问题的维数,降维处理的方式使算法在处理离线航迹规划问题时表现更稳定,但也容易使算法输出的航迹偏离最优航迹。

本文针对上述元启发式群体智能算法应用于无人机离线航迹规划时的两个问题,研究基于自适应郊狼优化算法(self-adaptive coyote optimization algorithm, SACOA)的无人机离线航迹规划方法。建立无人机离线航迹规划的数学模型,包括规划空间的表示、航迹的初始化方式以及代价函数的建立。随后在郊狼优化算法(coyote optimization algorithm, COA)的基础上设计4种不同性质的操作算子和一种自适应学习机制,并设计莱维飞行策略,提高算法的运算效率和全局搜索能力。最后利用基准函数评测算法的性能并进行航迹规划仿真实验分析。

1 数学模型

1.1 规划空间模型

无人机的飞行轨迹表示为一系列离散空间点序列{,,,…,,},和分别为航迹规划的起点和终点,,,…,为需要规划的中间节点,在三维离线航迹规划中,=×3为规划问题的维数。

本文仿真实验设计的无人机任务环境包括地形模型和威胁模型。原始地形建模读取某一区域的数字地形高程图,通过双线性插值建立一个连续的地形模型,原始地形是一块44.64 km×46.98 km的矩形区域,威胁区域建模为半径为3 km,高为2.5 km的圆柱体。

相对于一般最优化问题,离线航迹规划问题解具有一定特点,其解在解空间的分布不是无序的,而是一条可执行的飞行轨迹。由此本文设计一种椭圆初始化方式,如图1所示。

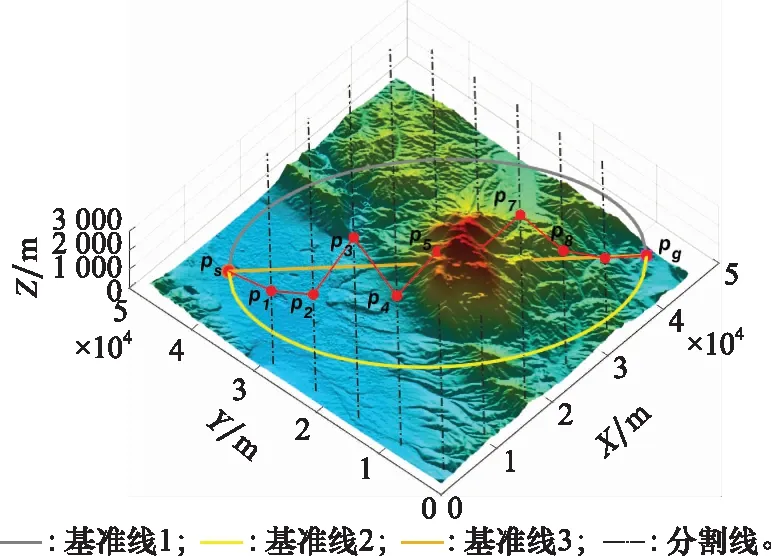
图1 离线航迹规划的初始化方式Fig.1 Initialization of offline path planning

根据航迹点可能的分布情况,以规划的起点和终点为椭圆长轴的两个端点建立一个椭圆方程,以椭圆的上半圆、下半圆和长轴作为基准线,根据航迹点的个数生成条分割线等分椭圆的长轴,在每一条基准线附近应用正态分布生成航迹点的、坐标,同时满足、坐标在分割线上,坐标以不与地形碰撞为约束在规划空间中按均匀分布随机生成。图1是以椭圆长轴为基准线的初始化示例。椭圆初始化方式让离线航迹规划问题的解初始化在最优解附近,缩小了算法在解空间的搜索范围,从而提高元启发式群体智能算法在应对高维复杂离线航迹规划问题时的稳定性。

1.2 约束模型

无人机航迹规划过程中需要考虑各类约束条件。

(1) 最大转弯角约束。无人机转弯的角度受其机动性能的约束,不能超过一定范围。设允许的最大转弯角为,第个航迹点的空间坐标为(,,),第段航迹在水平面的投影可表示为=(--1,--1),则最大转弯角约束可以描述为

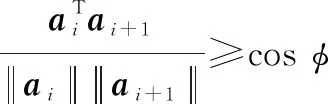
(1)

(2) 最大爬升、俯冲角约束。无人机的最大爬升、俯冲角受无人机的推力、机动性能的影响。设无人机允许的最大爬升、俯冲角为,则该约束可表示为

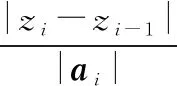
(2)

(3) 最小相对飞行高度约束。无人机在执行任务时需要与地面保持一定距离避免发生碰撞,设第段航迹段最低点的相对高度为,则该约束可表示为

≥

(3)

(4) 最短航迹段约束。受无人机机动性能的影响,无人机在改变航向之前有一个最短的直飞距离,设第段航迹的长度为,则该约束表述为

≥

(4)

1.3 代价函数模型

无人机离线航迹规划问题的代价函数是评估航迹优劣的标准,代价函数主要考虑的因素有任务要求、航迹长度和无人机约束条件。将航迹点序列表示为向量=(,,…,3),设()为目标函数,()为约束条件函数,则离线航迹规划问题可描述为

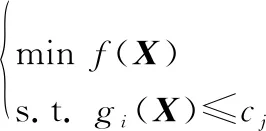
(5)

本文以航迹的总长度为搜索目标,将约束条件以罚函数形式表示,由此代价函数()可表示为

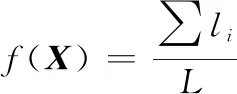
(6)

()=()+∑()

(7)

式中:表示从航迹起点到终点的直线距离;为第个约束函数的惩罚因子。

2 SACOA

2.1 COA

COA是2018年由Pierezan等人提出的一种新型元启发式群体智能算法,它通过模拟郊狼种群的生物特性来寻找优化问题的解。COA在应用于高维度多峰多约束的优化问题时,不易早熟,全局搜索能力较强,但它也存在可操作性不高、适应能力较差的问题。

COA主要有4个步骤:郊狼种群的分组与初始化、组内郊狼的成长、郊狼的出生与死亡、郊狼在组与组之间的驱赶与接纳。

郊狼种群的初始化主要包括设置种群的数量,分组的个数以及每组的个数,其中=×。设置算法停止的条件:最大迭代次数或算法运行时间限制。根据最优化问题的维数,以向量形式表示每一头郊狼,第次迭代第组的第个个体的表达式如式(8)所示,对于没有明显特征的一般最优化问题,每个郊狼个体的每一维按照式(9)进行初始化,随后按照式(10)计算每头郊狼的适应度值。

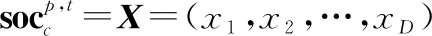
(8)

=lb+(ub-lb)

(9)

fit=()

(10)

式中:lb和ub分别表示郊狼个体第维社会因子的上限和下限,=1,2,…,,表示优化问题的维数;表示[0,1]范围内服从均匀分布的随机数;(·)表示适应度函数。

组内郊狼的成长主要考虑每组的最优个体、每组的组文化趋势、以及在每组随机选择的两个个体cr和cr。组文化趋势在算法中以每组的中位数个体表示。式(11)～式(15)表示了郊狼种群中每个个体的成长方式。

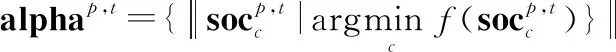
(11)

(12)

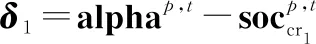
(13)

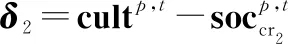
(14)

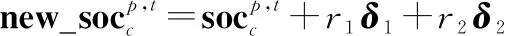
(15)

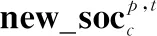
在一次迭代得到一个新解后,根据贪婪策略决定是否接受该新解:

(16)

郊狼的出生与死亡。幼年郊狼的诞生受组中随机选择的父母郊狼和环境因素的共同作用,式(17)表示了幼年郊狼的诞生过程:

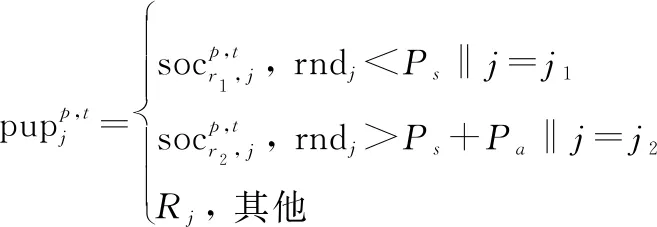
(17)

式中:和为在组随机选择的两个父郊狼序号;和为优化问题的两个随机维度,确保两个父代的基因一定能够遗传给子代;rnd为[0,1]内均匀分布的随机数;为在优化问题第维范围内产生的随机数,表征着环境因素的影响;和分别为分散概率与关联概率,决定着新诞生的郊狼受父代和环境影响的比率,其计算表达式为

=1

(18)

=(1-)2

(19)

为保证种群的个数不变,在幼年郊狼出生后,根据其社会适应度值决定幼年郊狼的生与死:当组内存在比幼年郊狼适应度差的郊狼时,幼年郊狼存活,适应度值最差的个体死亡,当新出生的郊狼适应度值在组内最差时,则幼年郊狼直接死亡。

郊狼的驱赶与接纳。郊狼开始是随机分配到某一组群中,为保证种群的活力,增强组与组之间的信息交流与联系,郊狼在成长的过程中,有一定概率离开它所在的组而进入其他组,其概率为

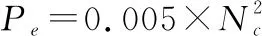
(20)

2.2 SACOA

COA以组群中随机两个个体与最优个体、“组文化”之间的差值来引导组群中个体在解空间搜索,相比于粒子群算法、灰狼算法等传统仿生智能群算法的操作算子,这种操作算子是一种间接启发信息模型,在解空间中探索未知空间的能力比较强,全局搜索能力强,但存在搜索效率较低、可操作性不高的问题。

本章提出SACOA,在COA的基础上,设计4种不同的操作算子,让算法搜索中每个个体根据自适应学习机制智能选择合适的操作算子,同时去除COA中个体生与死步骤,让种群在搜索过程中小概率做随机方向的莱维飞行。

2.2.1 操作算子与自适应学习机制设计

COA中操作算子和贪婪策略引导种群中个体向着最优解收敛,但对于不同优化问题、不同个体,由于个体所处的位置不同、解决的问题性质不同,每个个体趋向于收敛位置的路径是不同的,采取同一操作算子效率较低,由此本文设计4种操作算子,并设计一种自适应智能学习机制,使种群中每一个个体在每次迭代中,根据自身的情况,智能选取合适的操作算子,增加有效迭代的次数,提高算法收敛速度以及全局搜索能力。以下是4种操作算子的表达式:

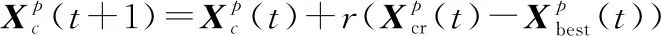
(21)

(22)

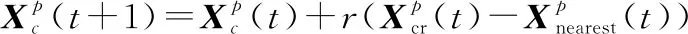
(23)

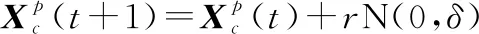
(24)

在SACOA中,引导信息包括每组的最优个体、组文化趋势、最邻近的个体以及变异因子,智能学习机制是为了在贪婪策略下,针对不同问题、不同个体,让每个个体每次迭代选择最合适的操作算子,减少无效迭代的次数,提高算法的收敛速度与全局寻优能力。以下是自适应学习机制的描述。

对于每个粒子,每种操作算子的初始选择概率为025,在自适应智能学习机制中,第个个体选择第个操作算子的概率为():

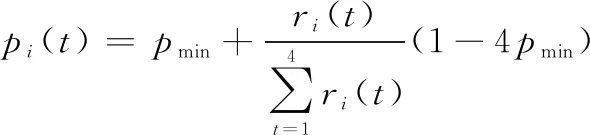
(25)

式中:表示最小概率,本文设置为01;()表示第个个体选择第个操作算子的回报函数,其计算表达式为

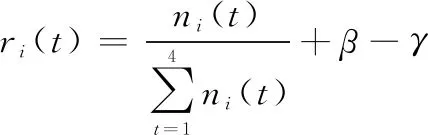
(26)

式中:()为第个个体选择第个操作算子成功改善个体适应度值的次数;和分别为奖励因子和惩罚因子,当上一次选择第个操作算子,若成功改善个体适应度值则奖励因子置为一个正值,本文取01,若没有改善适应度值则惩罚因子置一个正值,本文取01,其他情况置0。

222 莱维飞行策略设计

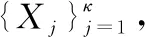
莱维飞行在应用于搜索未知空间方面有很多实例,文献[27]数据表明用莱维飞行和布朗运动可以表述海洋生物的捕食运动。文献[28-30]研究表明合理地应用莱维飞行能有效改善算法的搜索能力。

莱维飞行相对于其他类型的随机游走而言,有相对较高的概率出现大的跨步,属于一种短距离和长距离相间混合的行走方式。在数学描述中,莱维分布是一种幂函数分布:()～e-,在实际应用中一般用Mantegna算法模拟莱维飞行:

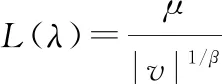
(27)

式中:=-1,一般取常数15;和服从正态分布:

(28)

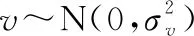
(29)

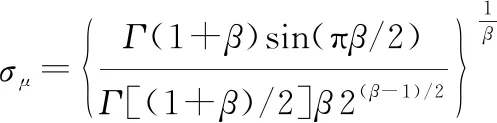
(30)

式中:(·)为伽马函数;=1。

本文设置在迭代过程中,个体以小概率做莱维飞行:

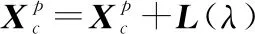
(31)

综上,SACOA的操作步骤如下。

设置初始参数:种群个数,分组数,每组的个体数量,莱维飞行概率;

初始化郊狼种群,并计算每个个体的适应度值;

每个个体根据式(25)计算每个操作算子的选择概率,并按概率选择操作算子;

根据所选择的操作算子计算个体的值,根据式(16)更新个体的值并更新个体的适应度值;

每个个体按概率,根据式(31)进行随机方向的莱维飞行;

每个组群之间按式(20)规定的概率进行“驱离”与“接纳”操作;

判断是否达到终止条件,若是则输出最优个体,否则重复步骤3～步骤7。

3 仿真实验与分析

本文首先利用基准函数测试SACOA的性能,随后进行离线航迹规划仿真实验验证SACOA应用于无人机离线航迹规划的有效性。实验程序由C#语言编写,Visual Studio 2019平台运行。SACOA和COA的公共参数设置如下:=100,=5,=20,SACOA莱维飞行的概率设置为=0.01。

3.1 基准函数测试与对比

为了验证SACOA应用于高维复杂函数时的性能,本文采用来自CEC2017的复杂函数进行实验验证。CEC2017的测试函数包含30个不同特性的函数:单峰函数(F1～F3)、单一多峰函数(F4～F10)、混合多峰函数(F11～F20)和组合多峰函数(F21～F30)。所有测试函数的维数设置为=50,每一维的搜索区间为[-100,100]。选取用于对比的元启发式群体智能算法包括PSO、GA、GWO、COA。

考虑到公平对比,所有算法的公共参数保持一致。PSO、GA、GWO的参数采取默认参数。最大迭代次数设置为10 000次,每种算法独立实验50次。实验结果如表1所示。

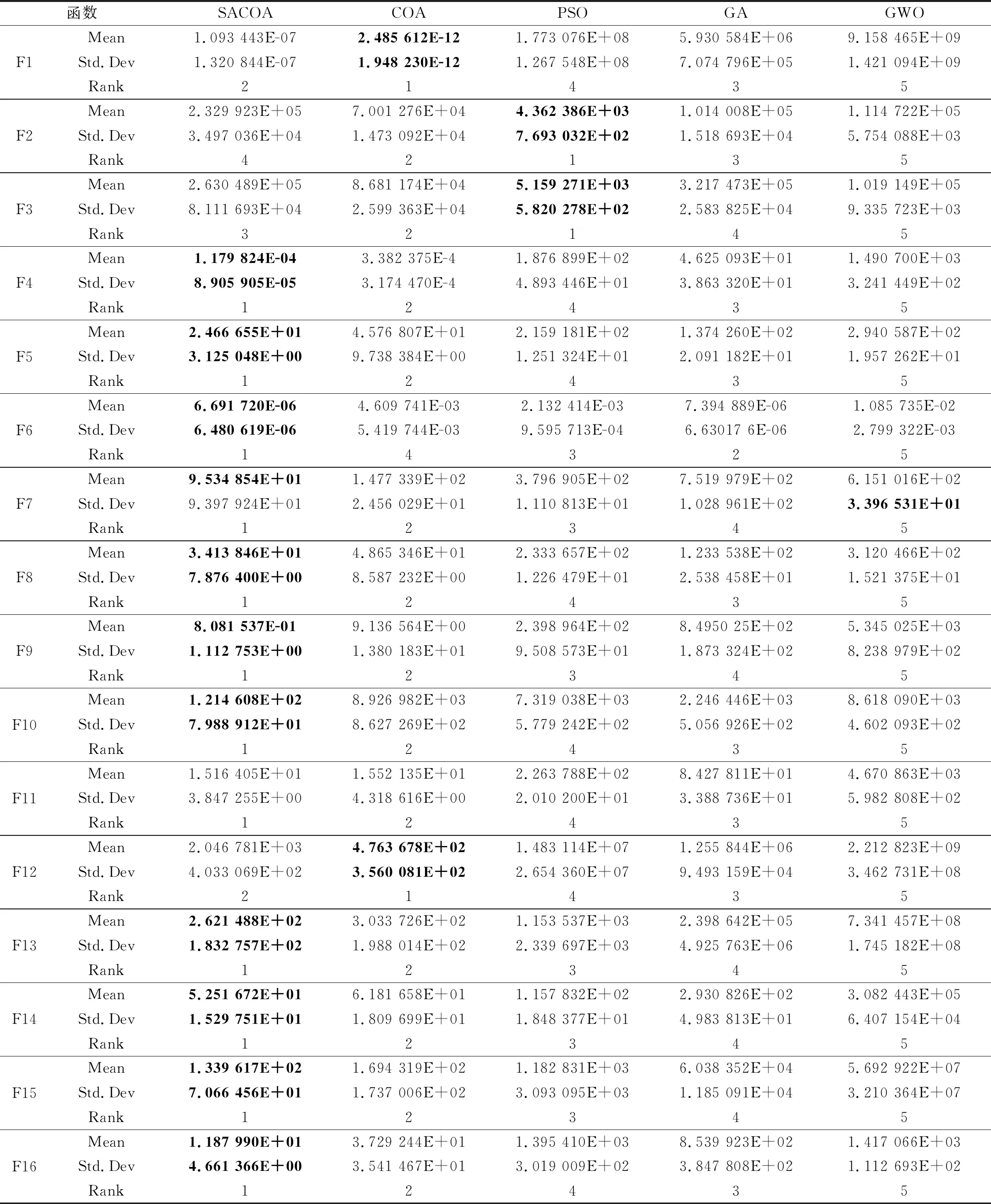
表1 SACOA和其他算法在CEC2017测试函数上的性能对比

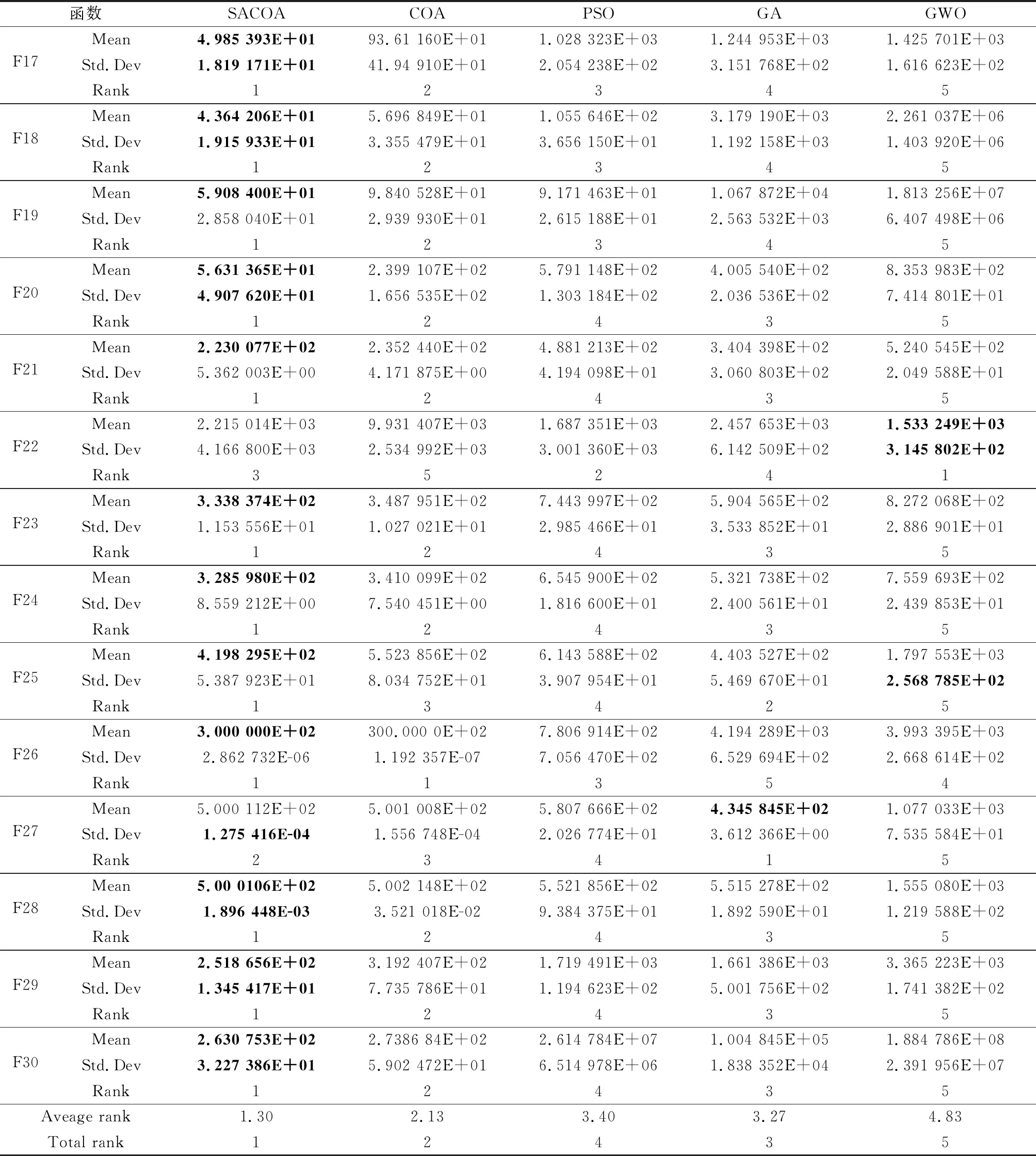
续表1

本文采用均值(Mean)和标准差(Std.Dev)来评估一个算法的寻优能力和稳定性能。均值越小表示算法的寻优能力越强,标准差越小则表示算法稳定性越好。同时给每个算法在每一个函数的表现进行排名(Rank),并统计每一种算法的平均排名与总体排名。由表1可以看出:① 在30个高维测试函数中,SACOA和COA整体平均排名分别位居第一和第二,SACOA在24个函数测试中排名第一,COA在3个测试函数中排名第一,在23个测试函数中排名第二,由此表明SACOA和COA在应对高维复杂最优化问题时的性能优势明显;② 进一步观察发现,SACOA、COA相较于GA、PSO、GWO的优势主要是单一多峰函数、混合多峰函数和组合多峰函数,单峰函数主要考察算法的局部开发能力,多峰函数主要考察算法的全局搜索能力,由此可知SACOA、COA的优势是应对复杂高维多峰最优化问题时,具有较强的全局搜索能力,不易陷入局部最优,这与离线航迹规划的要求十分契合;③ SACOA相对于COA,在25个多峰复杂函数上的表现有不同程度的提高,这表明SACOA相较于COA进一步提高了应对多峰复杂最优化问题时的全局探索能力。

COA采取贪婪策略,每个个体的每次迭代只会接受适应度得到改善的操作,每一次接受称为一次有效迭代,图2为在单一多峰函数、混合多峰函数、组合多峰函数中分别选取两个函数,画出SACOA、COA一次运算中每个个体的平均有效迭代次数的条形图,由图2可以看出,SACOA相比于COA,在相同的最大迭代次数情况下,有效迭代次数均有不同程度的提高,这使得SACOA搜索效率更高,探索未知空间的次数更多,能更均匀地搜索解空间,这是SACOA全局寻优能力更强的原因,表明了本文设计的自适应学习机制和莱维飞行策略的有效性。

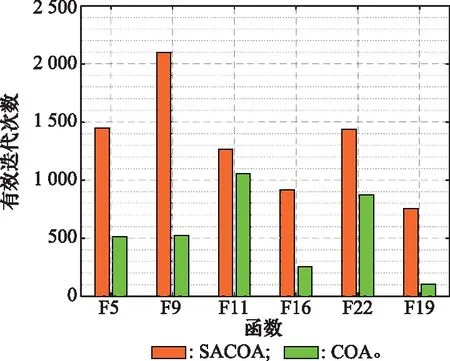
图2 有效迭代次数对比Fig.2 Comparison of effective iterations

综上,SACOA具有良好的全局搜索能力,不易早熟,适用于解决高维多峰的复杂最优化问题。

3.2 离线航迹规划仿真

为了验证本文所提策略应用于无人机离线航迹规划的有效性,本节在三维环境下分别使用SACOA、COA、GA、PSO进行航迹规划。仿真条件设置:约束条件设置为最大转弯角=45°,最大爬升、俯冲角=30°,最小航迹段=1 000 m,最低相对高度=100 m。航迹规划的起点为(5 670,41 670,1 000)m,终点为(42 030,2 349,800)m。最大迭代次数为5 000次。

图3为分别设置10个(30维)、20个(60维)、30个(90维)航迹点,应用SACOA、COA、GA、PSO进行重复实验50次,得到的平均代价以及其上下波动范围。由图3可以看出,在30～90维范围内,随着航迹规划问题维数的上升,算法规划得到的航迹代价值整体是上升的,SACOA在不同维数的条件下均取得了最优的效果,航迹平均代价最小,上下限波动范围也是最小的。同时,可以看出当航迹规划问题维数设置为30维时,4种算法规划得到的航迹代价相差较小,当问题维数上升时,尤其是90维时,SACOA仍能保持较好的全局搜索能力,而其他3种算法规划得到的航迹代价均具有较大幅度的上升。

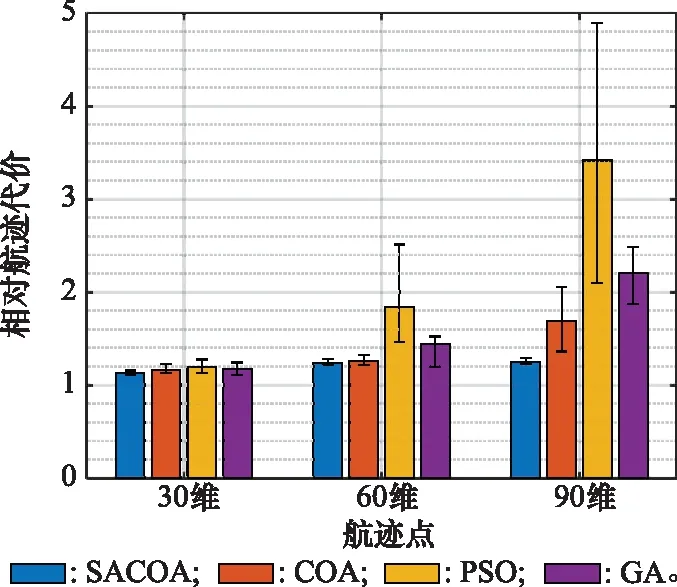
图3 SACOA和其他算法规划的航迹相对代价Fig.3 Cost of the path planned by SACOA and other algorithms

图4为设置20个(60维)航迹点时,SACOA、COA、GA、PSO规划结果对比。由图4可以看出,相较于GA、PSO和COA,SACOA规划的航迹曲折更小,更平滑,相对高度更低,航迹长度更短,表明SACOA规划的航迹质量更高。图5为航迹代价随迭代次数的变化曲线,由图5可看出,SACOA的相对代价值最小,表明SACOA的航迹最优。同时可以看出PSO、GA收敛很快,在不到1 000次时就陷入了局部最优,而SACOA和COA收敛较慢,在2 000～3 000次时航迹代价还有微弱的改善,这表明SACOA和COA在应用于无人机离线航迹规划时有良好的全局搜索能力。同时可以看出,SACOA相比于COA达到同一代价值所需的迭代次数更少,表明SACOA的效率更高,全局寻优能力更强,也表明本文提出的操作算子、自适应学习机制和莱维飞行策略的有效性。

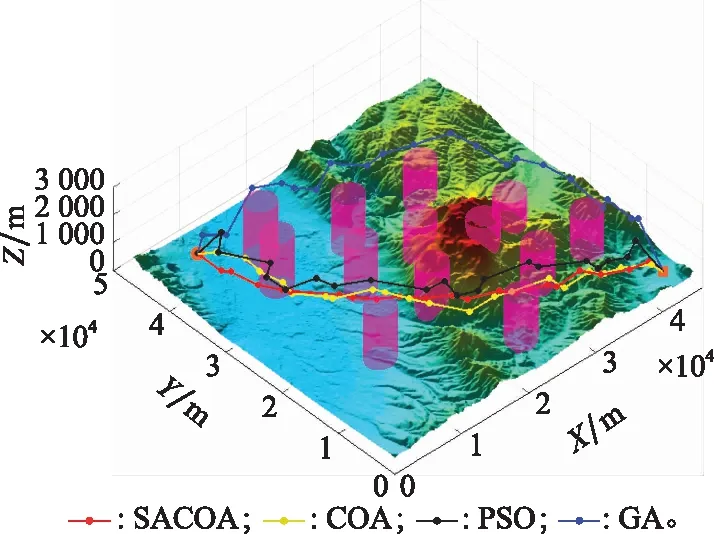
图4 航迹规划结果对比Fig.4 Comparison of path planning results

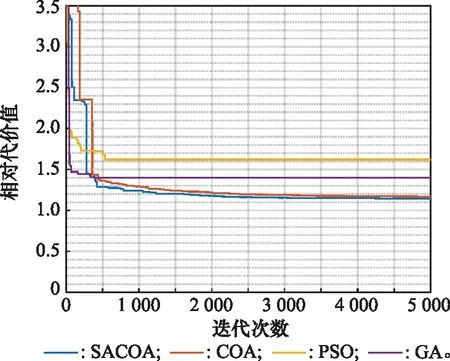
图5 航迹代价随迭代次数变化曲线Fig.5 Curve of cost with the number of iterations

综上离线航迹规划仿真,SACOA应用于无人机离线航迹规划时具有良好的全局搜索能力,能适应不同维数的离线航迹规划问题。

4 结 论

本文提出了一种SACOA,在原始COA的基础上设计了4种操作算子和一种自适应学习机制,让种群中的郊狼个体每次迭代智能选择合适的操作算子,同时设计了莱维飞行策略,提高了算法的搜索效率和全局搜索能力。进行了函数测试与航迹规划仿真分析,函数测试表明SACOA具有良好的搜索效率和全局寻优能力,适合解决多峰高维最优化问题,航迹规划仿真实验表明SACOA能很好地处理不同维数的无人机离线航迹规划问题,具有良好的工程价值。