房屋建筑混凝土施工地表沉降预测方法

刘 同

（吕梁学院，山西 吕梁 033001）

1 房屋建筑混凝土施工地表沉降预测方法

1.1 房屋建筑混凝土施工地表沉降影响因素分析

房屋建筑混凝土施工产生的地表沉降通常会受到多种复杂因素的影响。因此，为对地表沉降进行有效预测，需要对其影响因素进行具体分析[1]。地表沉降的影响因素具体可分为4个部分，分别是地质因素、房屋建筑设计因素、施工因素以及周边环境因素，具体分析过程如下。

首先，水文地质因素主要包括地下水位因素以及土体结构。房屋建筑区域下的地下水位如果过高或遇到汛期水位升高，都会引起地表沉降的变化。通常情况下，地下水位与土体的密度与强度有直接关系，因此地下水位会间接影响房屋建筑承重结构的荷载变化，进而对房屋建筑区域内土体的内应力产生影响，使地表发生沉降。在土体结构方面，地表沉降通常与土体的实际密度相关[2-3]。土体的密度越大，强度越大，则土体结构的承载力也会越大，进而不容易发生变形，也不容易使地表产生沉降。而土体密度主要的影响因素为内摩擦角与土壤含水量，其中土体内摩擦角越大，地表沉降越慢；土壤含水量越高，地表沉降越快[4]。

其次，房屋建筑设计因素主要包括建筑的尺寸以及支护结构的类型[5]。在同一土体上进行房屋施工，建筑设计的平面尺寸越大，则地表沉降越大；平面尺寸越小，地表产生的沉降也就越小。因此在对地表沉降进行预测时，除了要考虑地面因素，房屋自身的尺寸信息也需要纳入考量范围。房屋建筑的支护结构一般包括连续墙和围护桩，不同的支护结构对地表沉降的影响强度也有所不同。一般来说，为了判断一个房屋建筑的支护结构会对地表沉降产生多大的影响，可以采用测量支护结构刚度的方式[6]。支护结构的刚度越大，对外力的承载性能也就越强，因此也就不容易发生地表沉降。

再次，施工因素具体包括现场的施工排水以及施工开挖深度。一般房屋建筑施工需要在无水的环境下进行，为此需要在施工时将开挖面的地下水位降低到1 m以下，施工排水工作做得越好，土体的结构越密实，久越不容易使地面发生沉降。而施工开挖深度一般与地表沉降量呈正相关，因此在对地表沉降进行预测时，需要结合房屋建筑的设计高度以及地下开挖深度2个因素[7]。

最后，周边环境因素主要包括管线分布情况以及建筑物分布情况。当房屋建筑施工的周边存在较多其他建筑物或者地下埋藏了多条管线时，随着荷载力的不断加大，该区域土体的压力也会变大，进而使房屋建筑周围的地表发生沉降。因此在进行地表沉降预测时需要考虑周边建筑以及管线的排列密度。

根据上述对地表沉降影响因素的分析，结合层次分析法（AHP，Analytic Hierarchy Process），构建出如图1所示的分析方案。

图1 房屋建筑无凝土施工地表沉降影响因素

AHP的分析原理中包括指标层A、目标层B以及基准层C。该文通过上述步骤对地表沉降的影响因素进行分析，以此为后续的地表沉降预测提供理论支持。

1.2 地表沉降影响因素权重值计算

根据层次分析法的原理，结合上述对地表沉降影响因素的具体分析，构建地表沉降判断矩阵，记为B=（bij）n×n，其中bij代表目标层的各项影响因素，此时该矩阵具有以下性质，如公式（1）所示。

由于该矩阵具备传递性，因此该判断矩阵可满足公式（2）。

式中：bjk和bik分别为其他横向目标层影响因素。

为对该判断矩阵的一致性进行确定，定义一致性指标为C，如公式（3）所示。

式中：λmax为判断矩阵的最大特征值；n为影响因素的总个数。定义最大特征值对应的特征向量为wi，则层次排序表达式如公式（4）所示。

根据上述构建的一致性指标可计算出一致性比率，具体如公式（5）所示。

式中：Ri为单次排序指标。

当CR值小于0.1时，说明此刻的排序结果一致性较高。根据排序结果对矩阵进行乘法运算，即可得到每个影响因素的具体权值[8]。根据上述步骤即可计算出地表沉降影响因素的权重值，为沉降预测提供数据支持。

1.3 构建地表沉降预测模型

本次地表沉降预测模型采用BP神经网络算法进行构建，结合上述计算出的地表沉降影响因素权值，对预测数据样本进行确定。假设神经元个数为i，第j个元素输出的矢量为xj，则对应的权重值设为wij，对该值进行动态调整，具体计算如公式（6）所示。

式中：yi为实际输出结果；di为期望输出矢量；a为动态调整步幅参数。

如果期望输出值与实际输出值之差过大，超过了阈值控制范围，则需要对其进行重新调整，直到二者之差在阈值范围内为止。对此，需要引入一个比例因子帮助权值进行调整，具体如公式（7）所示。

式中：Δwab为节点a与b之间的权值；s（k）为比例因子；ς（k）为节点处的误差幅值；oa（k）为节点处的激活程度；γ为学习效率；k为迭代次数。

比例因子的具体表达式如公式（8）所示。

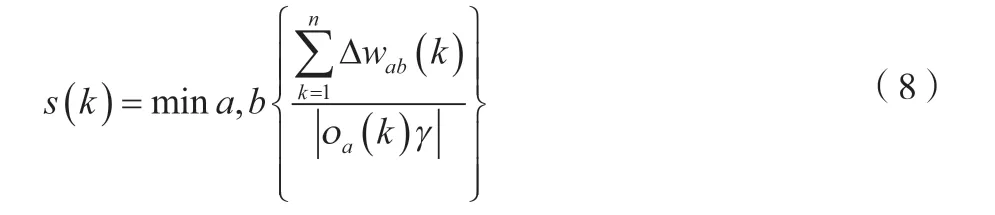
由此构建出的基于BP神经网络的地表沉降预测模型结构如图2所示，其中C1～C8分别代表基准层的8个影响因素。

图2 BP网络神经结构

根据上述步骤即可构建出地表沉降预测模型，结合上述提到的地表沉降影响因素分析以及权重值计算，至此，房屋建筑混凝土施工地表沉降预测方法设计完成。

2 试验部分

为证明该文提出的房屋建筑混凝土施工地表沉降预测方法在预测精度上优于传统的地表沉降预测方法，在理论部分设计完成后进行试验验证，以此对该预测方法的实际预测效果进行分析。

2.1 试验准备

本次试验的试验数据来源于某市地铁站附近的房屋建筑区域的历史数据，整片区域占地面积为20.23 km2，土体组成较为复杂，主要土质包括杂填土、砂岩、风化板岩、风化泥岩、风化灰岩、粉质黏土以及圆砾等，土层厚度为10 m～25 m，地下水位位于地表下约4.5 m处，土体含水量为25.43%。该区域为温带季风气候，地表径流与地下径流均受季节降雨量影响较大，降水年际变化量较大导致土体含水量变化浮动较大。通过实地勘测，该文获取了该区域下的相关参数，包括水文参数、土体参数以及建筑尺寸参数等。

为确保试验结果的准确性，该文在使用3种地表沉降预测对试验对象进行分析时，将所有基础数据进行了预处理，以保证预测结果不受数据变量的影响。数据预处理主要为归一化，将基础数据的变化范围固定在[0，1]，以此减少模型的运算难度，具体的归一化公式如公式（9）所示。

式中：Xk与Yk分别为输入数据与输出数据；Xmax和Xmin分别为输入数据中的最大值与最小值。

为提高试验结果的可靠性，本次试验选取2种传统的地表沉降预测方法作为对比对象，分别是基于机器学习算法的地表沉降预测方法以及基于灰色模型的地表沉降预测方法。该文算法的参数设置见表1。本次试验共选取10组不同时段的历史数据，进行10次对比试验，通过采用3种预测方法对该区域的历史数据进行预测，得到地表沉降预测曲线，并与实际预测情况进行对比，比较预测精度。

表1 算法参数设置

2.2 试验结果

本次试验选取的评价指标为预测方法与实际沉降情况的拟合程度，拟合程度越高，说明该方法的预测精度越高，也就越能对房屋建筑混凝土施工地表沉降的情况进行科学预测。具体试验对比结果如图3所示。

图3 地表沉降预测曲线对比

从上述试验结果可以看出，应用不同的预测方法对不同时段的房屋建筑区域进行预测时，其预测的精度也会有所不同。通过观察预测方法预测出的沉降量与实际地表沉降量之间的差距可以明显看出，2种传统的地表沉降预测方法得到的预测结果与实际情况相差较大，预测误差最高可达0.25 m以上，说明传统预测方法的预测精度较差。而该文提出的房屋建筑混凝土施工地表沉降预测方法得到的预测结果与实际地表沉降量差距较小，预测曲线的拟合程度也较高，由此可说明该文提出的预测方法具备较高的预测精度。

3 结论

该文提出的房屋建筑混凝土施工地表沉降预测方法通过采用层次分析法对影响地表沉降的关键因素进行了有效分析，采用权重值计算的方法对影响因素进行了排序。在此基础上构建出的地表沉降预测模型能够结合多方面影响因素，输出较为科学可靠的预测结果，能够满足对地表沉降的预测需求。