基于Fluent的风扇流场分析及结构参数优化设计

杨 欢 李庆武

（1．常州刘国钧高等职业技术学校，江苏 常州 213100；2．河海大学物联网工程学院，江苏 常州 213022）

0 引言

冷却风扇作为汽车发动机冷却系统的核心部件，其流量直接决定了汽车的散热性能。传统的设计通常采用理论公式与现场试验相结合的方法，或根据经验对风扇进行设计，存在周期长、成本高以及参数与性能匹配性差等问题[1]。

随着仿真技术的发展，国内外学者基于计算流体力学（CFD）研究了风扇不同的设计参数对其流量、功率以及效率等气动性能参数的影响[1-8]。张若楠等[1]基于Fluent分析风扇的3种不同参数对散热器进风量和风扇有效功率的影响规律。金涨军[2]基于CFD采用正交试验法研究叶片安装角、弦长和拱高对风扇静压和功率的影响并对其进行优化。郑智方等[3]采用正交试验研究风扇性能，以降低噪声。由此可见，基于Fluent采用正交试验法对风扇叶片进行结构参数优化设计可以有效地提高风扇的综合性能。

该文以提高冷却风扇的流量为目的，采用UG建立冷却风扇的三维模型，基于Fluent进行叶片流场仿真分析，并通过风洞试验进行理论验证。采用正交试验法，以背压为350 Pa时的流量为优化目标，以叶片数量、安装角以及叶片长度为优化参数，从而优化风扇的性能。

1 风扇流场建模与分析

1.1 风扇流场建模与网格划分

以某企业某型号冷却风扇为原型（如图1所示），采用UG建立简化后的三维几何模型。模型主要包括叶片、轮毂和外环3个部分。其中，冷却风扇的安装角为35°，叶片数为7，叶片长度为76 mm。

图1 冷却风扇几何模型

为了与风洞试验结果进行对比验证，CFD仿真模型的构建根据实际风洞试验模型进行设置。 为了使模拟状态下的气流更均匀，整个流场分为3个部分（进口域、旋转域和出口域）。

1.1.1 旋转域

试验中的叶片始终处于匀速转动状态，为了更好地模拟气体的流动情况，在风扇周围建立圆柱形包络体作为内流域，半径大小与实际风扇外壳大小相同，圆柱体前后表面稍微超出风扇端面（便于网格划分），如图2所示。

图2 旋转域

1.1.2 外流场

根据实际模型，实验台外部区域为进口，内部区域为出口，因此将外流场分为2个部分（进口区域和出口区域），如图3所示。

图3 进口域与出口域

由于风扇叶片造型复杂，因此采用非结构化四面体网格进行网格划分。为了更好地捕捉叶片周围区域的气流情况，对叶片处的旋转域网格进行细化，添加膨胀层和面网格。通过开展网格无关性验证，分别计算当背压为350 Pa、网格数量不同（约为210万、320万和400万）时的流量，结果表明，网格数为210万与320万的流量相差较大，约为3.5%；网格数为320万与400万的流量相差较小，约为1.0%。综合考虑计算精度和效率，采用网格数约为320万的网格（如图4所示）。

图4 整体网格

1.2 边界条件设置

该文冷却风扇模型所用到的边界条件包括压力进口、压力出口、壁面和交界面。由于空气为不可压缩流体，进、出口分别与大气相连通，因此将进、出风口边界条件分别设置为压力进口和压力出口。入口为大气压力，因此在多种工况条件下的相对压差均为0 Pa。根据风洞试验，将出口压力的背压分别设置为0～500 Pa。将长方体其余表面和圆柱外表面设置为壁面，将圆柱体与长方体的交界面设置为交界面。

1.3 计算方法设置

由于风扇的各个叶片表面都存在弯曲、扭转的情况，导致流体的运动并不规则，因此选择更贴合实际情况的Realizablek-ε模型，近壁处理选用增强壁面处理（Enhanced Wall Treatment）；当设置求解器时，采用SIMPLEC算法，以提高收敛速度；动量守恒方程、湍流动能和湍流耗散率均设置用二阶迎风格式来进行计算。

1.4 仿真结果及分析

对原始风扇实物进行CFD流场仿真分析，当背压为350 Pa、转速为4 425 r/min时，风扇的静压云图如图5所示。由图5可知，叶片的压力只有在尾缘处为负值，其余部分为正值，最大压力值为1 200 Pa，最小压力值为-1 270 Pa。在叶片的吸力面，处于叶片前缘靠叶片中间位置的表面静压值最小，同时向两侧逐步扩张；外环与叶片前缘相交处表面的静压值最大，并朝轮毂方向呈逐渐减小的趋势。

图5 冷却风扇表面静压图

原始风扇表面的速度云图如图6所示。由图6可知，风扇表面速度随直径的变大逐渐变大。风扇叶片在工作时受旋转离心力的作用，随着半径逐渐变大，风扇表面的旋转速度也开始变大，叶片表面的动压也逐渐增加。

图6 冷却风扇表面速度云图

通过改变出口边界条件，赋予风扇不同的背压值，可以得到不同背压下的风扇流量，如图7所示。当静压为350 Pa时，风扇的流量为0.38 m3/s。流量随静压的增大而逐渐减小。当静压为0 Pa时，冷却风扇的流量最大，约为0.99 m3/s；当静压为500 Pa时，流量达到最小值，约为0.28 m3/s。

图7 不同背压下风扇的流量

2 风洞试验验证

企业提供的风扇气动性能风洞实验台示意图如图8所示。实验台采用定静压的方式来测量相关参数和风量。首先，设定静压值，采用PID仪表测得静压值。其次，读取当前静压下的各项数值，例如大气压、差压、静压以及出风口风速等数值，以计算流量。最后，得到不同背压下的流量数据。

图8 风洞实验台

背压为100～400 Pa的流量试验值与数值解对比如图9所示。对比试验值与数值解可以看出，随着背压的增大，二者均变小。数值解均小于测试值，平均误差约为8.8%；当背压为200 Pa时，误差最小，约为2%。造成误差的原因主要有2点：1） 实验台存在一定的测试误差。2） 仿真分析时对模型进行了简化，导致模型存在一定误差。综合考虑误差的原因和结果，可以认为仿真模型和结果是准确、可靠的。

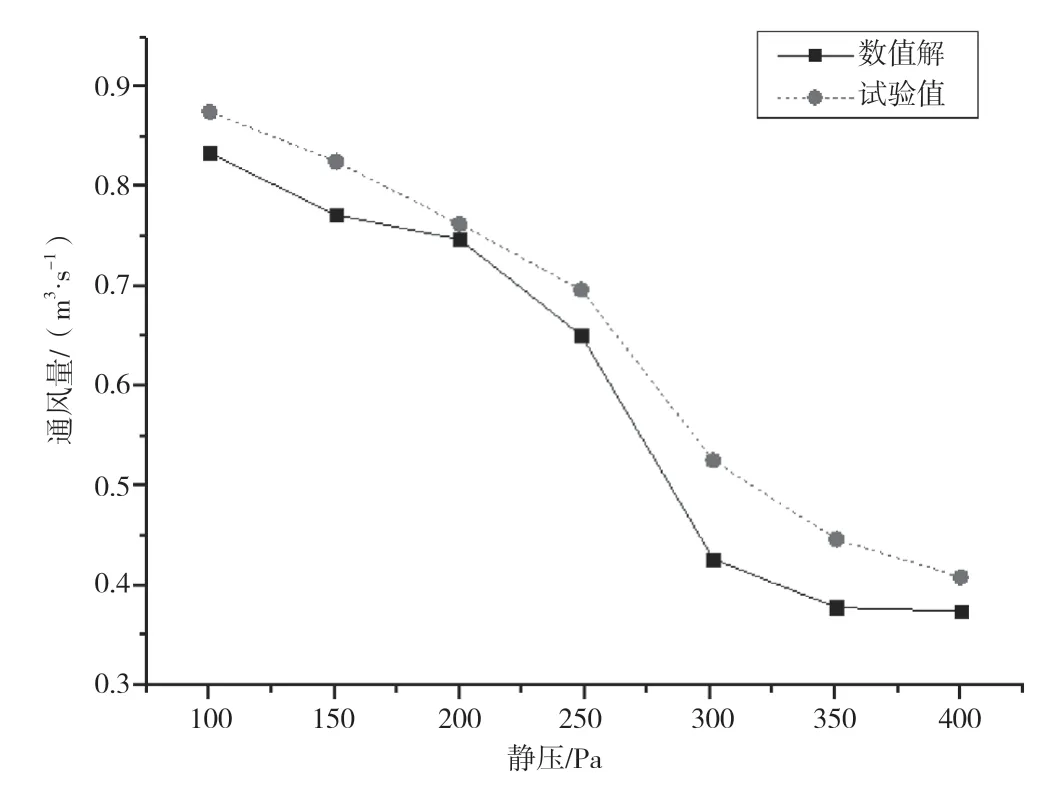
图9 数值解与风洞试验值对比

3 正交试验法优化设计

3.1 正交试验表

以企业提供的风扇原型为参考，采用正交试验法进行优化设计。所设计的风扇要求在尺寸限制的条件下，尽可能提高各背压下的流量。由于实际应用中最常用的为高背压段（300 Pa～450 Pa），因此选取背压为350 Pa时的流量作为评价指标。所设计的风扇内径、外径尺寸已限制，当风扇叶片过长时，会导致成本增加、风扇安装困难；当叶片过短时，会导致气流在叶片尖部产生过大的涡流，因此风扇的叶片长度变动范围较小，取75 mm、76 mm以及76.5mm。由于当叶片数过多时会导致摩擦损失增大，降低效率，因此叶片数取5片、6片以及7片。原始叶片的安装角为35°，试验中变换安装角，取33°、35°以及37°。

综上所述，选取叶片长度、数目以及安装角作为试验因子，每个试验因子各取3个水平。不考虑因子间的交互作用，共形成9种试验模型（见表1），查询正交表格选择L9（33）（正交表，共9列（三水平三因素））进行正交试验。

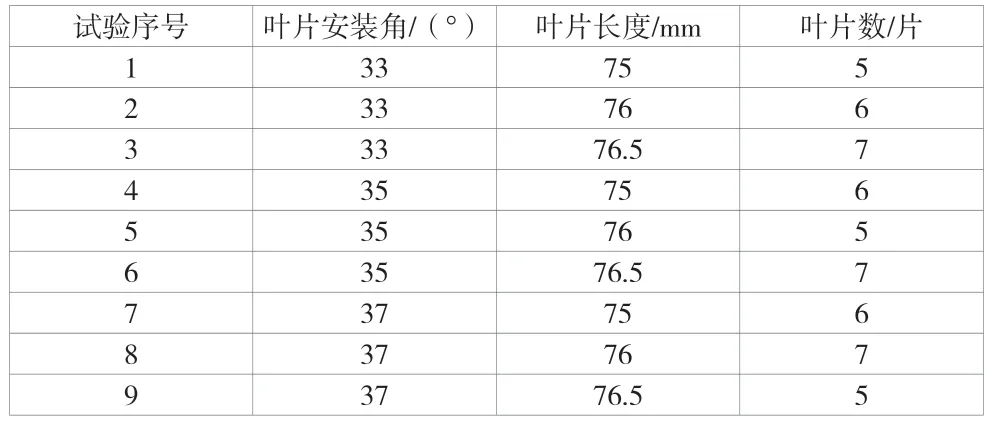
表1 正交试验表

3.2 正交试验结果分析

根据给定的模型进行仿真试验，结果见表2。K1、K2以及K3分别代表在各个因素、各个水平下的流量的总和，单位为m3/s；ki（i=1，2，3）表示任一列上因素取水平i时所得流量的算术平均值,单位为m3/s。极差Rm为各个因素的不同水平对冷却风扇流量的影响，极差值越大表示该因素的变动对评价指标的影响越大。

由表2可知，叶片数量、安装角和叶片长度3个因素及3个因素所对应的水平值对流量均有不同程度的影响。通过极差分析3个因素的显著性和各因素的最优水平值可得，对试验结果影响最大的是叶片数目，其次是叶片长度，影响最小的是安装角。由分析结果可知，第三个模型的流量为0.434 m3/s，比原始设计模型的流量增加了14.2%。最优叶片的参数为安装角33°，叶片长度76.5 mm，叶片数7片。

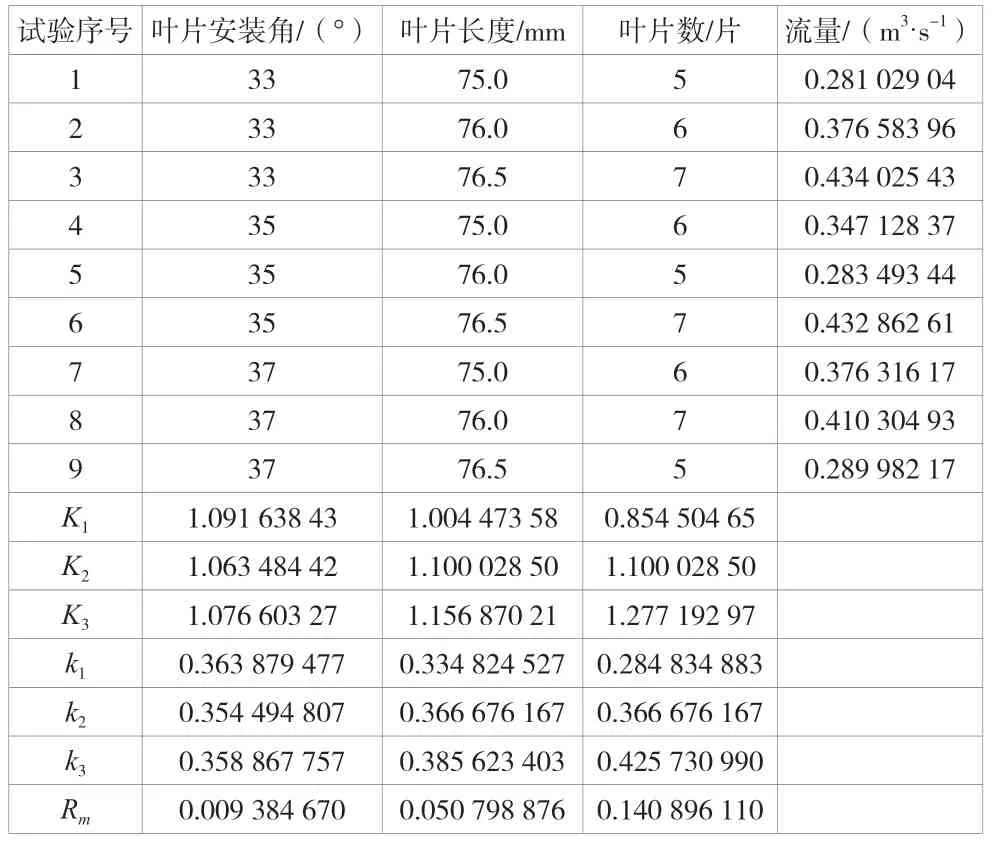
表2 正交试验结果极差分析

为了更直观地看出因素与指标的关系，以因素水平为横坐标，流量平均值ki（i=1，2，3）为纵坐标，得出流量随叶型参数的变化规律。风扇安装角与流量的关系如图10（a）所示，随着安装角的增加，风扇的流量先减少增加，在安装角为35°时取得最小值。风扇叶片长度与流量的关系如图10（b）所示，当叶片长度由75.0 mm增至76.5 mm时，叶片的流量由0.334 8 m3/s逐渐增至0.385 6 m3/s。其原因是随着叶片长度的增加，叶片与流体区域的接触面积变大，高速旋转时与流体的相互作用面积变大，从而使流量增大。流量随风扇叶片数的变化关系如图10（c）所示，随着叶片数由5片增至7片，风扇的流量呈持续增加的趋势，当叶片数目为7片时，流量达到最大值；当叶片数目为5片时，流量达到最小值，二者流量相差0.140 9 m3/s。其原因是随着叶片数目的增加，叶片与流体之间的接触面积呈倍数增加，因此风扇的流量呈正比例增长的趋势。

图10 流量与安装角、叶片长度和叶片数的关系

3.3 不同背压下优化前后对比

通过试验得到当背压为350 Pa时的流量最优结构参数，以此为基础，改变背压，得到不同背压下优化后的风扇的流量值，并将结果与原始结构的结果进行对比。结果如图11（a）所示，背压从0 Pa增至500 Pa，优化后的流量变化趋势与优化前的流量变化趋势基本一致，随着背压的增大而减少；且在各背压下，优化后的流量均优于优化前的流量。在实际应用中最常用的300 Pa、350 Pa以及400 Pa背压下，流量分别提高了约10.744%、14.830%和2.780%。

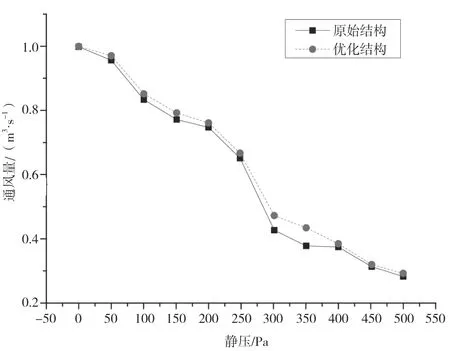
图11 原始风扇与优化风扇流量对比图

4 结语

该文基于Fluent对风扇叶片流场进行仿真分析，并采用正交试验法，以提高叶片流量为优化目标，以叶片安装角、长度以及数目为优化参数对叶片进行优化设计。结论如下：1） 叶片表面静压值最高在叶片前缘，随着出口背压的不断增大，流量逐渐降低。2） 优化后的冷却风扇在不同背压下的出口流量均有所提高，在实际应用中最常用的300 Pa、350 Pa以及400 Pa背压下，流量分别提高了约10.744%、14.830%和2.780%，有效地提高了风扇的工作性能。3） 风洞试验结果验证了数值仿真模型和方法的可靠性，对风扇的优化设计具有指导意义。