随机变量及概率分布列中常见误区剖析

侯有岐特级教师

(陕西省汉中市四〇五学校)

在随机变量及分布列的学习中，学生对概念理解不透、审题不严、考虑不周以及忽视公式成立的条件等，导致求解中出现“多解”或“漏解”等失误.本文对常见的易错、易混、易忘的典型问题归类整理，并进行错解剖析和警示展示，希望对学生的学习有所帮助.

1 忽视随机变量的取值范围，导致分布列所有事件概率之和不为1

例1某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有四次参加考试的机会，一旦某次考试通过，便可领取驾照，不再参加以后的考试，否则就一直考到第四次为止.如果李明决定参加驾照考试，设他每次参加考试通过的概率依次为0.6，0.7，0.8，0.9.求在一年内李明参加驾照考试的次数X的分布列.

错解随机变量X的可能取值为1，2，3，4，则

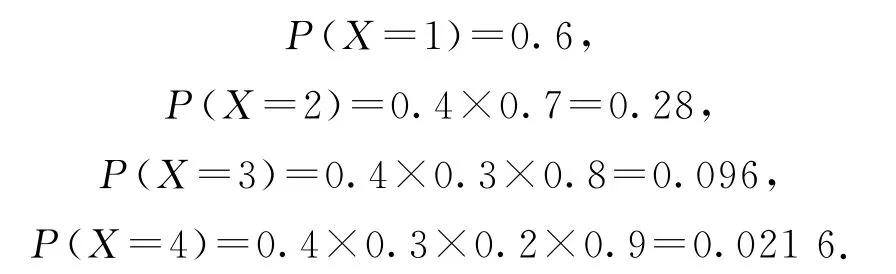
综上，所以李明参加驾照考试的次数X的分布列如表1所示.

表1

剖析对事件“X＝4”不理解，导致分布列所有事件概率之和不为1，“X＝4”表示李明前3次均没通过，而第四次可能通过也有可能不通过.

正解随机变量X的可能取值为1，2，3，4，则

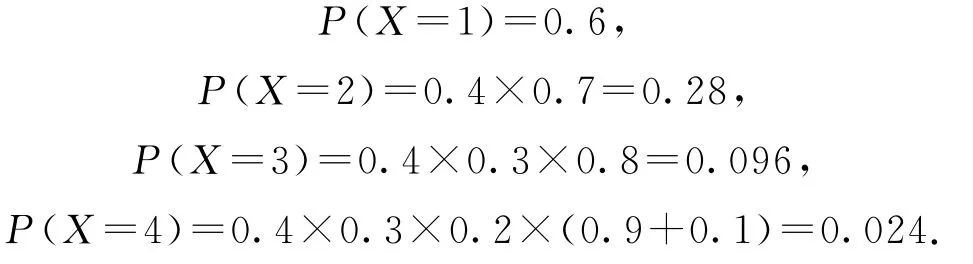
或利用性质求解，P(X＝4)＝1－P(X＝1)－P(X＝2)－P(X＝3)＝0.024.

综上，李明参加驾照考试的次数X的分布列如表2所示.

表2

警示在确定随机变量取值时，找出关键词，理解随机变量ξ的实际意义.准确列出随机变量ξ的所有可能取值，且注意ξ＝0是否符合题意，只有这样才可避免出错.有时可以用概率分布列性质p1＋p2＋p3＋…＋pn＝1检验分类是否完备或简化求解某个取值的概率.

变式某人进行一项试验，若成功，则停止试验，若失败，再重新试验一次.若试验3次均失败，则放弃试验.若每次试验成功的概率为求此人试验次数ξ的分布列.

解试验次数ξ的可能取值为ξ＝1，2，3，所以

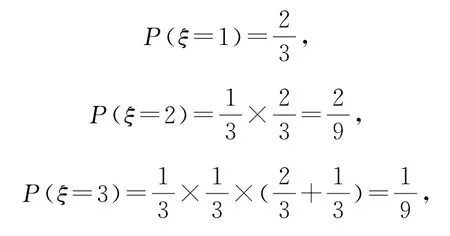
则随机变量ξ的分布列如表3所示.

表3

2 混淆二项分布与超几何分布

例2在装有4个黑球、6个白球的袋子中，任取2个，试求不放回地抽取，取到黑球数X的分布列及期望E(X).

错解随机变量X的可能取值为0，1，2.根据题意得X～B(2，0.4)，则从10个球中任取2个，其中恰有k个黑球的概率为P(X＝k)＝Ck20.4k0.62－k，k＝0，1，2.

因此，随机变量X的分布列如表4所示.

表4

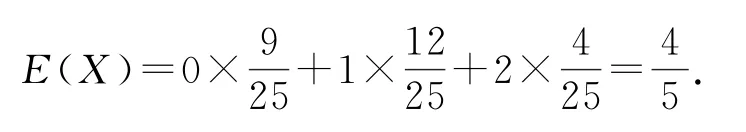
剖析本题是将二项分布和超几何分布混淆致误.事实上，超几何分布是不放回地抽取，即每进行一次试验，下一次再发生同一事件的概率已经发生了变化，即每次发生的概率都不相等，它实质上是古典概型的特例;二项分布是有放回地抽取，即每做一次试验，发生同一事件的概率相同.但他们确实有着密切的联系，样本容量越大，超几何分布和二项分布的对应概率相差越小，当样本个数无穷大时，超几何分布和二项分布对应的概率就相等，换言之超几何分布的极限就是二项分布.

正解随机变量X的可能取值为0，1，2.因为是不放回地抽取，所以X服从超几何分布.从10个球中任取2球的结果数为，从10个球中任取2个，其中恰有k个黑球的结果数为，那么从10个球中任取2个，其中恰有k个黑球的概率为

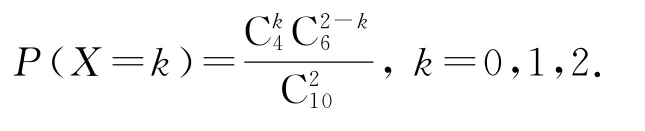
因此，随机变量X的分布列如表5所示.

表5

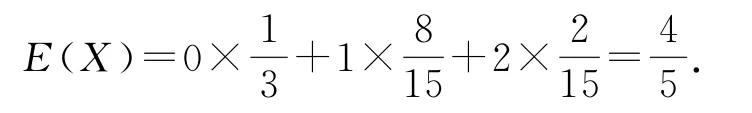
警示设在每次试验中成功的概率都为p，则在n次重复试验中，试验成功的次数用ξ表示，ξ服从二项分布，则在n次试验中恰好成功k次的概率为P(ξ＝k)＝Cknpk(1－p)n－k，E(ξ)＝np，D(ξ)＝np(1－p).超几何分布是在理解随机变量的意义下，把元素自然分成2组，利用组合数和古典概型概率公式得到分布列的一个通项公式，其本质是“不放回抽样”，是一种古典概型，而二项分布的随机实验是“独立重复实验”，强调每次实验的结果发生的概率相同，可认为是“有放回抽样”.

变式从1，2，3，…，100这100个数中，随机取出两个数，求其积是3的倍数的概率.

解基本事件数有种.在 由1到100这100个自然数中，3的倍数的数组成的集合M中有33个元素，不是3的倍数的数组成的集合N中有67个元素，事件A为任取两个整数相乘为3的倍数，分两类:取M中2个元素相乘有种;从集合M，N中各取1个元素相乘有种.因为这两类互斥，所以

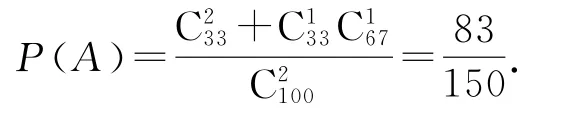
3 对概率模型中的各参数含义理解不清致错

例3从一批含有13只正品、2只次品的产品中，不放回地抽取3次，设抽得的次品数为ξ，求E(5ξ＋1).

错解1随机变量ξ～B(n，p)，这里独立重复试验的次数n＝3，在一次试验中事件(次品)发生的概率得

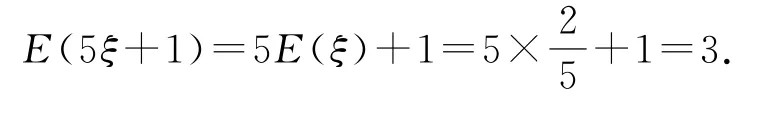
错解2因为不放回地取，先组合再排列，所以

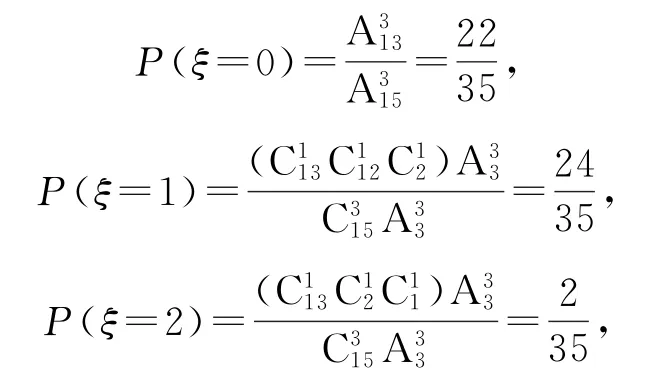
故

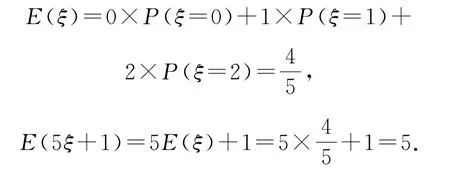
剖析错解1误认为随机变量是独立的，服从二项分布，而本题中变量与前后有关系，是不独立的，即变量不服从二项分布，不能用E(ξ)＝np计算期望.错解2中，对于ξ＝1这种情形，表示从13只正品中取1只正品后(不放回)，再接着从剩下的12只正品中取1只正品(不放回)，表示从2只次品取1只次品，这时，对这3只产品进行全排列，得()×.其实，13只正品被抽取的机会是均等的，取得的2只正品前后没有关系，应视作一种情形，只要看1只次品所取的位置，即有3种方法，则

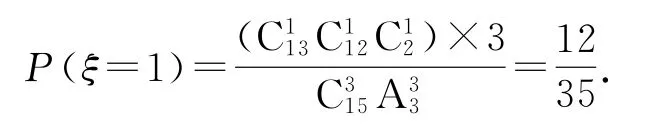
正解先选后排，正品、次品选定后注意正品为相同元素，只需要排定次品的位置就唯一确定了此时相同正品的位置，则

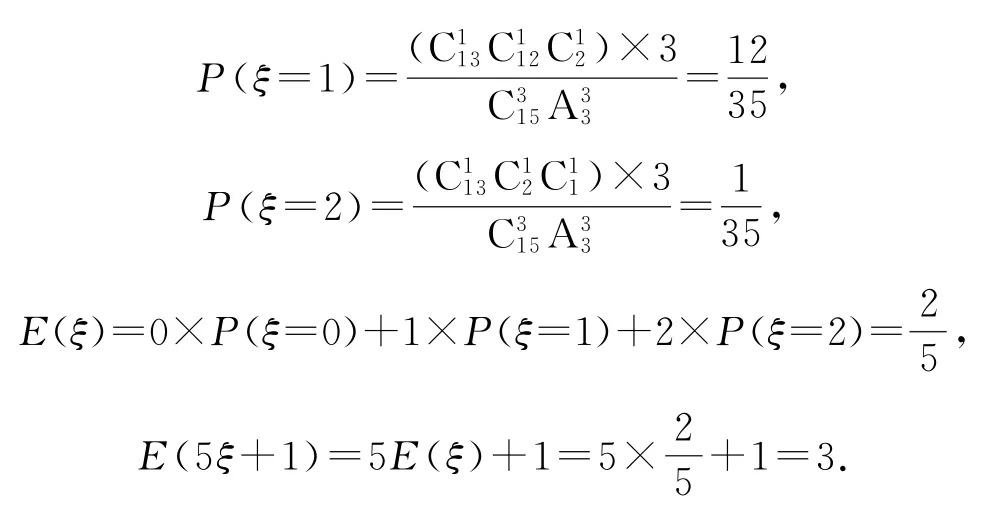
警示不放回地抽取，在理解随机变量取值的意义下，先选后排，且注意次品选定后正品是相同元素，与次品的位置是“一一”对应关系，排定次品就唯一确定了正品，利用这种对应关系就可以避免重复计数.

变式甲、乙两名篮球队员轮流投篮，直至有一人投中为止.设甲每次投中的概率为0.4，乙每次投中的概率为0.6，而且两人之间以及各次之间对投篮结果互不影响，设甲投篮的次数为ξ，且甲先投，则P(ξ＝k)＝( ).

A.0.6k－1×0.4 B.0.24k－1×0.76

C.0.4k－1×0.6 D.0.76k－1×0.24

解“ξ＝k”的正确含义是前k－1次甲、乙都没有投中，而第k次甲、乙两人中，若甲投中就结束;若甲未投中，则乙再投中后结束(因为是甲先投篮的).设Ak:甲第k次投中，Bk:乙第k次投中，则

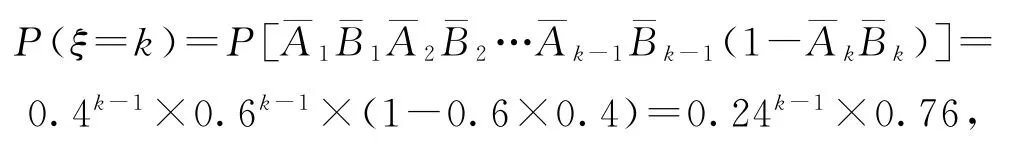
故选B.

4 对二项分布中各参数含义理解不清致错

例4已知甲、乙两名篮球运动员每次投篮命中的概率分别为甲、乙每次投篮是否投中相互之间没有影响，乙投篮3次均未命中的概率为

(1)求p的值;

(2)若甲投篮1次、乙投篮2次，两人投篮命中的次数之和记为X，求X的分布列和数学期望E(X).

错解(1)乙投篮的次数～B(3，p)，根据题意，得

(2)X＝0，1，2，3，当X＝0时，甲，乙两人投篮命中次数都为当X＝1时，甲，乙两人投篮命中次数为0，1或1，0，则

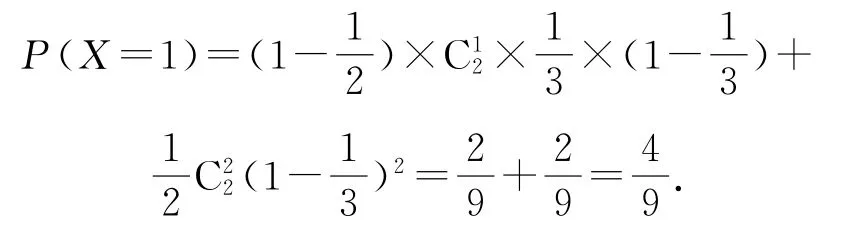
当X＝2时，甲，乙两人投篮命中次数为1，1或0，2，则

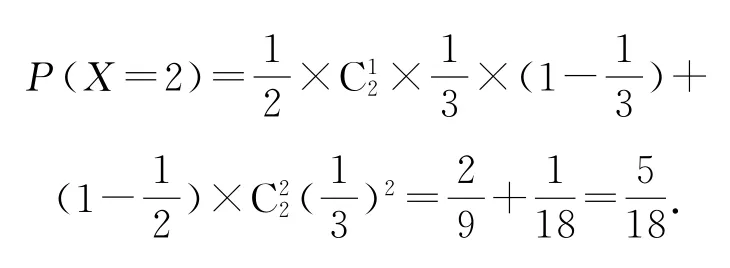
当X＝3时，甲，乙两人投篮命中次数为1，2，则

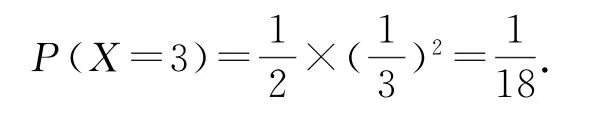
因此，X的分布列如表6所示.

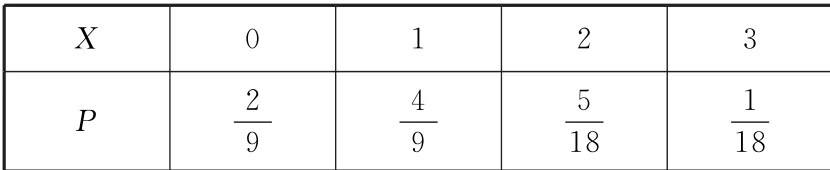
表6

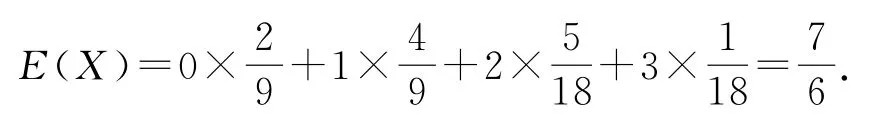
剖析(1)对二项分布中各参数含义不清导致p求错;(2)对随机变量X的取值的意义理解出错，应借助变量X的取值合理分类，每类下借助相互独立事件同时发生分步，每步中构建二项分布P(X＝k)＝Cknpk(1－p)k，k＝0，1，2，…，n的模型简化求解概率.

正解(1)乙每次投篮命中概率为p，投篮3次，命中次 数ξ～B(3，p)，由 题 意 得P(ξ＝0)＝

(2)甲投篮1次，乙投篮2次，命中次数之和X的可能取值为0，1，2，3，所以

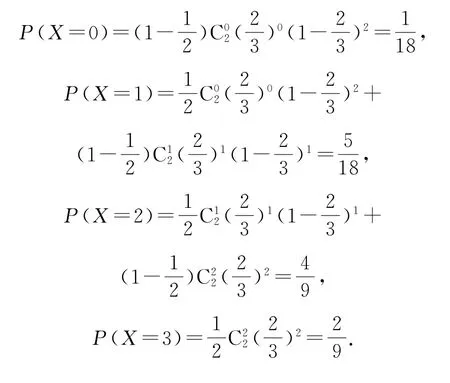
因此，X的分布列如表7所示.

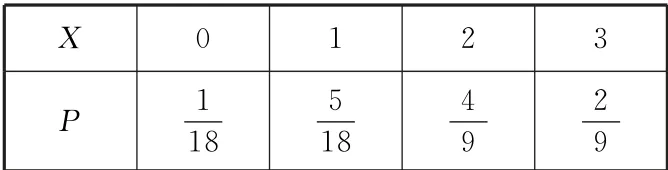
表7

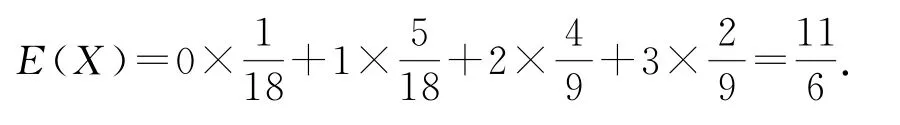
警示解答与二项分布有关的问题关键把握好:1)必须是n次独立重复试验;2)若每次试验中事件A发生的概率都是P，则在n次试验中，事件A恰好发生k次的概率为P(ξ＝k)＝Cknpk(1－p)n－k(k＝0，1，2，…，n);3)若ξ～B(n，p)，则

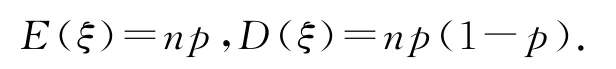
变式某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖.每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球.在摸出的2个球中，若都是红球，则获一等奖;若只有1个红球，则获二等奖;若没有红球，则不获奖.

(1)求顾客抽奖1次能获奖的概率;

(2)若某顾客有3次抽奖的机会，记该顾客在3次抽奖中获一等奖的次数为X，求X的分布列和数学期望E(X).

解(1)记事件A1＝{从甲箱中摸出的1个球是红球}，A2＝{从乙箱中摸出的1个球是红球}，B1＝{顾客抽奖1次获一等奖}，B2＝{顾客抽奖1次获二等奖}，C＝{顾客抽奖1次能获奖}，则由题意A1与A2相互独立，与互 斥，B1与B2互 斥，且B1＝A1A2，B2＝

又因为

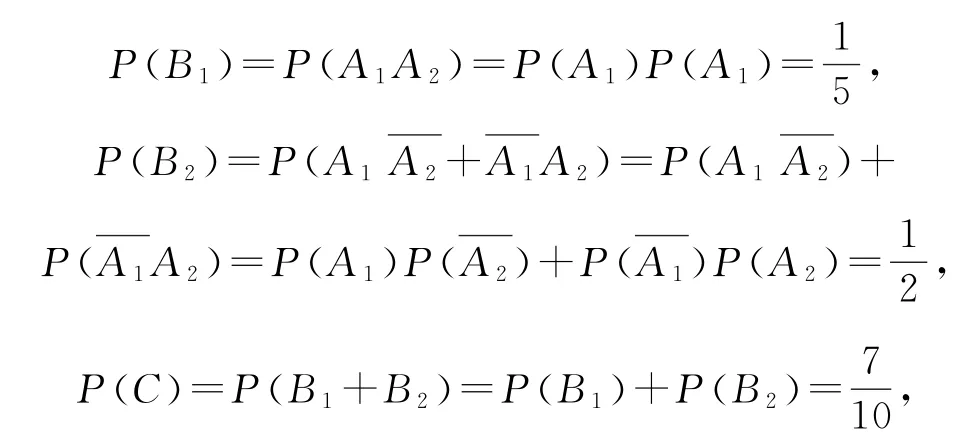
(2)顾客抽奖3次可视为3次独立重复试验，由(1)知，顾客抽奖1次获一等奖的概率为所以X～于是

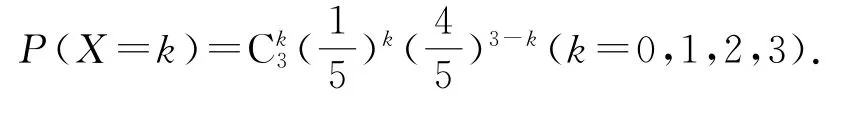
因此，X的分布列如表8所示.

表8

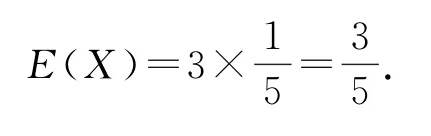
5 最值的求解中混淆“概率”“期望”的意义

例5某电器商经过多年经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列如下:

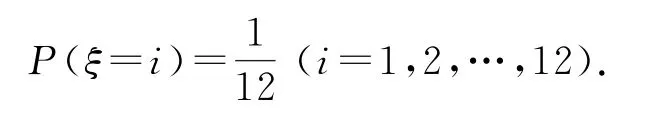
设每售出一台电冰箱，电器商获利300元，如销售不出而囤积于仓库，则每台每月需花保养费100元，问电器商月初购进多少台电冰箱才能使自己平均收益最大?

错解1由题意得

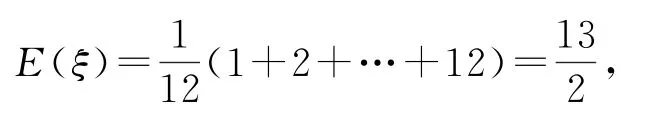
由期望的意义知:电器商月初购进6台或7台电冰箱才能使自己平均收益最大.

错解2设月初购进x台电冰箱，则获利也是随机变量，可能取值为

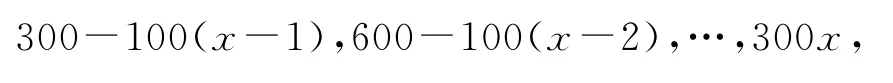
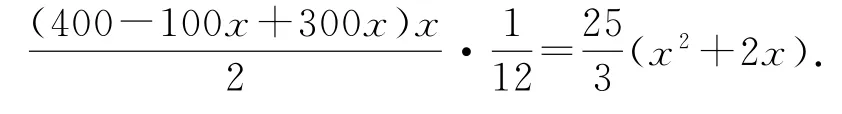
因为1≤x≤2，所以当x＝12时期望最大，所以月初购进12台电冰箱.

剖析错解1中，错把期望与实际等同，E(ξ)＝表示平均能卖台，不是一定能卖台.错解2中，当获利的取值为300x时，概率为也是错误的，误认为只有x台，卖出比x大的台数不可能.实际上当获利的取值为300x时，概率应为

正解设月初进x台，则获利η是一个随机变量，所有可能取值为300－100(x－1)，600－100(x－2)，…，300x，共x个值，分布列如表9所示.

表9

警示注意概率和期望与实际问题的区别，选准随机变量为主元，借助概率和期望的意义构建目标函数，利用函数性质求解概率中的最值问题.

变式一个口袋中装有n个红球(n≥5且n∈N*)和5个白球，一次摸奖从中摸两个球，两个球颜色不同则为中奖.

(1)试用n表示一次摸奖中奖的概率p;

(2)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为f(p)，当n取多少时，f(p)最大?

解(1)一次摸奖从n＋5个球中任选两个，有C2n＋5种，它们等可能，其中两球不同色有种，一次摸奖中奖的概率

(2)设每次摸奖中奖的概率为p，则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为

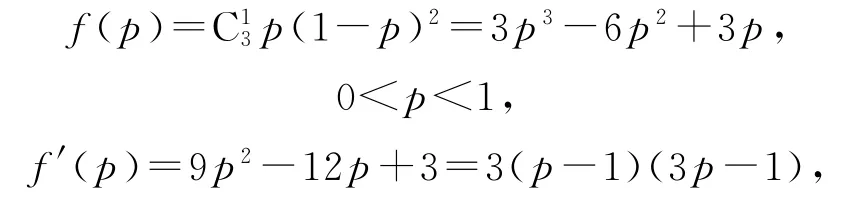
链接练习

1.体育课的排球发球项目考试的规则是：每位学生最多可发球3次，一旦发球成功，则停止发球，否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0)，发球次数为X，若X的数学期望E(X)＞1.75，则p的取值范围是( ).

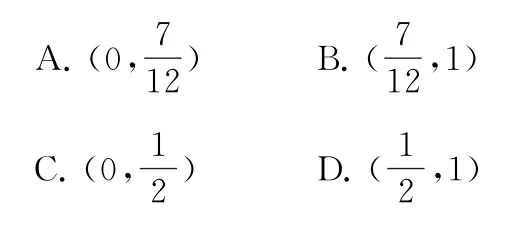
2.新型冠状病毒的传染性非常强，而且可以通过接触传播或呼吸道飞沫传播.该病毒进入人体后有潜伏期，并且潜伏期越长，感染他人的可能性越高，为此要进行隔离观察和核酸检测.

(1)现对100个病例的潜伏期(单位：天)进行调查，统计发现潜伏期的中位数为5，平均数为7.21，方差为5.08.假设潜伏期Z服从正态分布N(μ，σ2)，其中μ近似为样本平均数，σ2近似为样本方差.现在很多省份对入境旅客一律要求隔离14天，请用概率的知识解释其合理性.

若随机变量Z服从正态分布N(μ，σ2)，则

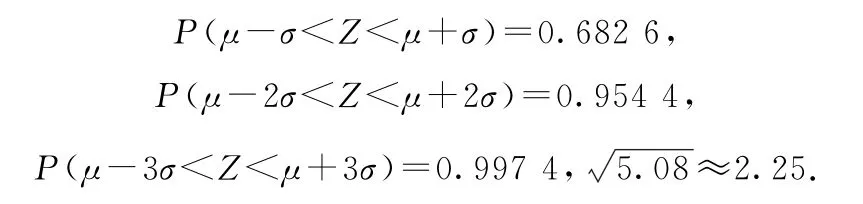
(2)现有n份(n∈N*)核酸样本，有以下两种检测方案：方案1：逐份核酸检测n次；方案2：混合检测，将其中k(k∈N*，k≥2)份核酸样本分别取样混合在一起进行检测，若检测结果为阴性，则这k份核酸样本全部为阴性，因而这k份核酸样本只要检测一次就够了；如果检测结果为阳性，说明这k份核酸样本中存在阳性，为了弄清这k份核酸样本中，哪些是阳性，就要对这k份核酸样本逐份检测，此时这k份核酸样本检测总次数为k＋1次.根据统计发现，疑似病例核酸检测为阳性的概率为p(0＜p＜1).现有5例疑似病例，对其采用上述两种方案分别检测.

(ⅰ)假设5例疑似病例的核酸样本中只有2份为阳性，若采用逐份检测方式检测，求恰好经过3次阳性样本全部被检出的概率；

(ⅱ)在新冠肺炎爆发初期，由于检测能力不足，核酸检测次数的期望值越小，则方案越优.若，现将该5例疑似病例样本进行核酸检测，问：方案1和方案2哪个更优?

链接练习参考答案

1.C.

2.(1)若潜伏期Z～N(7.21，2.252)，此时

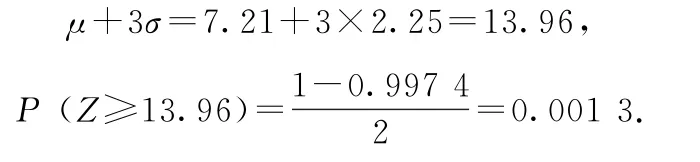
显然潜伏期超过14天的概率很低，因此隔离14天是合理的.

(ⅱ)方案2更优.