统计与成对数据的统计分析章节小测

尹承利

(山东省泰安英雄山中学)

(本试卷共22小题，满分150分，考试用时120分钟)

参考公式数据和公式

1.回归直线^y＝^bx＋^a的斜率和截距的最小二乘估计公式

2.线性相关中的相关系数公式r＝

χ2独立性检验中几个常用的小概率值和相应的临界值.

α 0.1 0.05 0.01 0.005 0.001 xα 2.706 3.841 6.635 7.879 10.828

一、单项选择题(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.)

1.某校不到40岁的教师有350人，40岁及以上的教师有140人，为了了解普通话在该校的推广普及情况，用分层抽样的方法，从全体教师中抽取一个样本容量为70人的样本进行普通话水平测试，则“不到40岁的教师”样本数为( ).

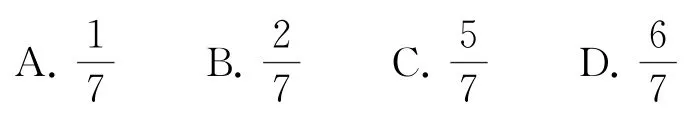
2.一个样本数据按从小到大的顺序排列为13，16，18，x，26，27，28，31，其中位数为22，则x是( ).

A.18 B.19 C.20 D.21

3.在下列两个分类变量X，Y的样本频数列联表中，判断X，Y之间有关系的是( ).

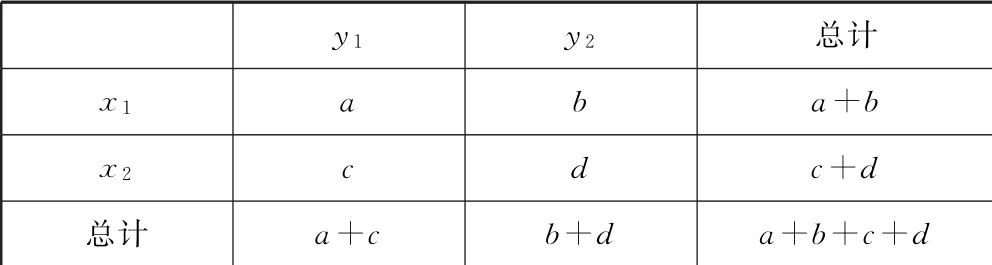
y1 y2 总计x1 a b a＋b x2 c d c＋d总计 a＋c b＋d a＋b＋c＋d

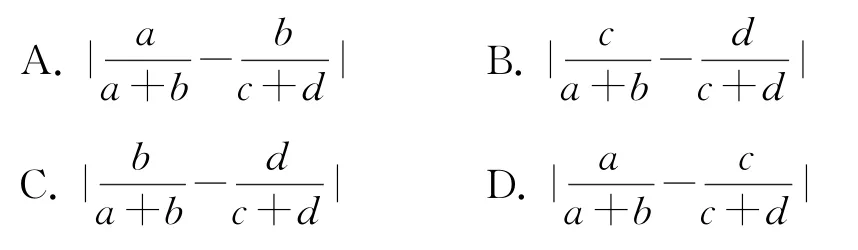
4.某校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40)，[40，60)，[60，80)，[80，100).若某班不高于60分的人数是15人，则60分是第( )分位数.

A.20% B.30% C.40% D.50%

5.某旅游城市为向游客介绍本地的气温情况，绘制了一年中12个月平均最高气温和平均最低气温的雷达图.图中点A表示10月的平均最高气温约为15℃，点B表示4月的平均最低气温约为5℃.下面叙述不正确的是( ).

A.各月的平均最低气温都在0℃以上

B.7月的平均温差比1月的平均温差大

C.3月和11月的平均最高气温基本相同

D.平均气温高于20℃的月份有5个

6.为了解某家庭人均用电量y(单位:kW·h)与气温x(单位:℃)的关系曾由下表数据计算出回归直线方程为^y＝－x＋50，现表中有一数据被污损(*处)，则被污损的数据为( ).

气温x/℃ 30 20 10 0人均用电量y/(kW·h) 20 30 * 50

A.35 B.40 C.45 D.48

7.2021年春节期间央视推出的“中国诗词大会(第6季)”在社会各界引起了巨大反响.为弘扬中华优秀传统文化，某中学举行了一次别开生面的“中国诗词”比赛活动，统计了甲、乙两班各6名学生比赛的成绩如图所示，设甲、乙两班数据的平均数依次为，标准差依次为s1，s2，则( ).

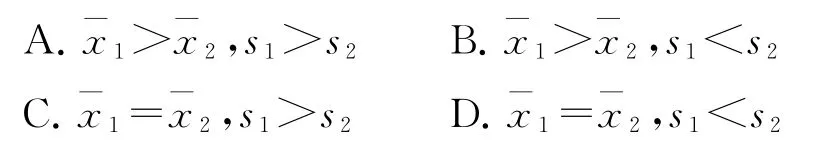
8.对具有线性相关关系的变量x，y有一组观测数据(xi，yi)(i＝1，2，…，8)，其回归直线方程是且x1＋x2＋…x8＝2(y1＋y2＋…y8)＝6，则当时，y的估计值为( ).

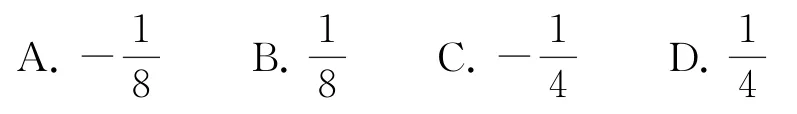
二、多项选择题(本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项是符合题目要求的.全部选对的得5分，有选错的得0分，部分选对的得2分.)

9.从某大学随机选取的8名女大学生，其体重y(单位:kg)与身高x(单位:cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1，2，…，8)，用最小二乘法建立的回归方程为^y＝0.849x－85.712，则下列结论中正确的是( ).

A.若某女大学生身高增加1cm，则其体重约增加0.849kg

B.若某女大学生身高为172cm，则可断定其体重必为60.316kg

C.若根据样本数据计算出样本相关系数为r＝0.798，则表明体重与身高有很强的正相关关系

D.若根据样本数据计算出相关指数为R2＝0.64，则表明女大学生的体重差异有64%是由身高引起的

10.下列说法正确的是( ).

A.一组数据可能有两个众数

B.将一组数据中的每个数据都减去同一个数后方差没有变化

C.一组数据的方差一定是正数

D.在样本的频率分布直方图中，一共有n个小矩形，若中间一个小矩形的面积是其余n－1个小矩形面积和的且样本容量为160，则中间一组的频数为32

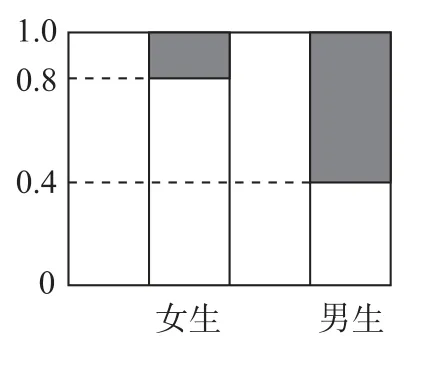
11.某中学的学生积极参加体育锻炼，如图是随机调查该中学高三年级男、女生各100名是否喜欢篮球运动的等高条形图，阴影部分的高表示喜欢该项运动的频率，则下列说法正确的是( ).

A.以题中样本的频率作为概率，则该中学高三年级学生喜欢篮球运动的概率为

B.有99.5%的把握认为该中学高三年级学生是否喜欢篮球运动与性别无关

C.有99.9%的把握认为该中学高三年级学生是否喜欢篮球运动与性别有关

D.性别决定是否喜欢篮球运动

12.经验表明，一般树的胸径(树的主干在地面以上1.3m处的直径)越大，树就越高.由于测量树高比测量胸径困难，因此研究人员希望由胸径预测树高.下面给出某林场在研究树高与胸径之间的关系时收集的某种树的数据(如表)和绘制的线性回归方程的残差图.

编号 1 2 3 4 5 6 7 8 9 10 11 12胸 径/cm 18.1 20.1 22.2 24.4 26.0 28.3 29.6 32.4 33.7 35.7 38.3 40.2树 高/m 18.8 19.2 21.0 21.0 22.1 22.1 22.4 22.6 23.0 24.3 23.9 24.7

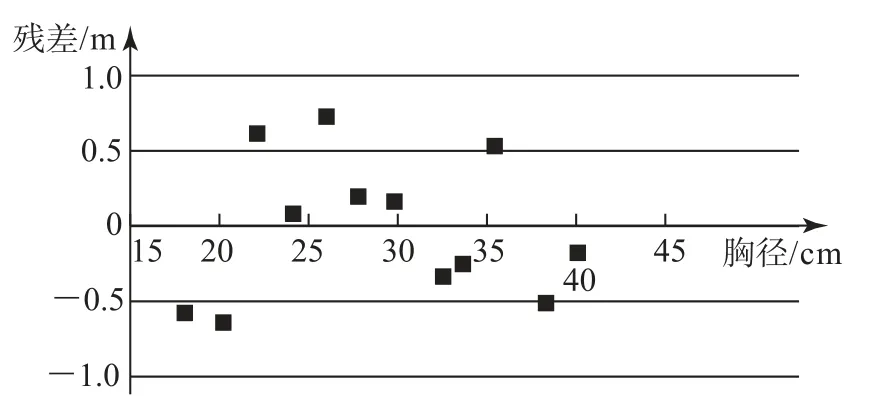
根据上表和残差图，则下列说法正确的是( ).

A.树高y与胸径x之间具有正相关关系

B.斜率^b≈0.2499

C.预测当树的胸径为50.6cm时，树的高度约是31.467m

D.由残差图可知线性回归方程的拟合效果较好

三、填空题(本题共4小题，每小题5分，共20分.)

13.高二(1)班有男生28名，女生22名，在一次数学模块检测中，男生的平均分是121分，女生的平均分是119分.则该班全体学生的平均分是_________分.

14.在某项才艺竞赛中，有9位评委，主办单位规定计算参赛者比赛成绩的规则如下:剔除评委中的一个最高分和一个最低分后，再计算其他7位评委的平均分作为此参赛者的比赛成绩.现有一位参赛者所获最高分为86分、最低分为45分，若未剔除最高分与最低分时9位评委的平均分为76，则这位参赛者的比赛成绩为_________分.

15.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩(百分制)得到2×2列联表.

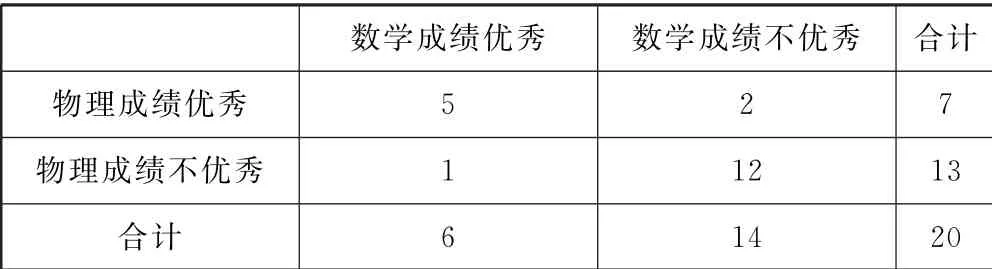
数学成绩优秀 数学成绩不优秀 合计物理成绩优秀 5 2 7物理成绩不优秀 1 12 13合计 6 14 20

根据表中的数据计算，你有_________的把握认为学生的数学成绩与物理成绩之间有关系.

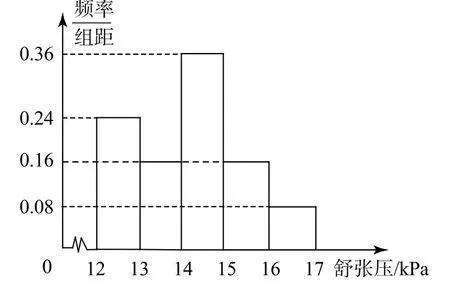
16.为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位:kPa)的分组区间为[12，13)，[13，14)，[14，15)，[15，16)，[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组.右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为_________;第2人是第_________分位数(第一空2分，第二空3分).

四、解答题(本题共6小题，共计70分.解答应写出文字说明、证明过程或演算步骤.)

17.(10分)某中学高二年级有男生520人，女生480人，按男、女生进行分层，通过分层抽样的方法，得到男、女生在某次考试中数学学科的平均成绩分别为110.6分和108.2分.

(1)如果在各层中按比例分配样本，总样本量为100，那么在男、女生中分别抽取了多少名?

(2)在(1)的情况下，请估计高二年级全体学生的平均成绩.

18.(12分)某运动生理研究课题组统计了10名长跑运动员和10名同龄非运动员的心率(单位:次/分)，并绘制了如右图所示的茎叶图.

(1)根据茎叶图比较运动员和非运动员哪类人群的心率较高，哪类人群的心率较稳定;

(2)用平均数和方差检验(1)中所得结论是否正确.19.(12分)2022年北京冬奥运动会即第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京和张家口举行，某研究机构为了了解大学生对冰壶运动的兴趣，随机从某大学生中抽取了100人进行调查，经统计男生与女生的人数比为9∶11，男生中有20人表示对冰壶运动有兴趣，女生中有15人对冰壶运动没有兴趣.

(1)完成2×2列联表，并判断能否有99%的把握认为“对冰壶运动是否有兴趣与性别有关”?

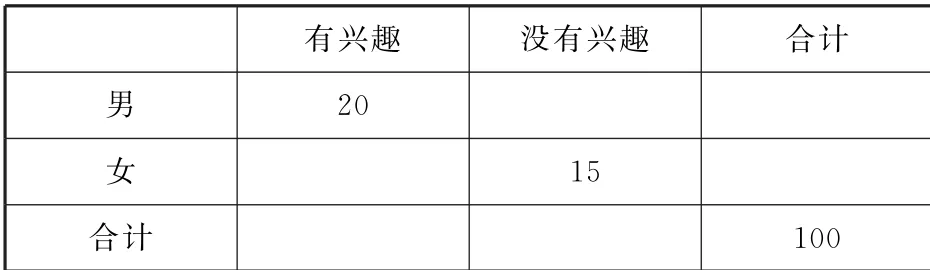
有兴趣 没有兴趣 合计男20女15合计 100

(2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取6人，求抽取的男生和女生人数.

20.(12分)某高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表.

组频数 频率[85，95) ① ②[95，105) 0.050[105，115) 0.200[115，125) 12 0.300[125，135) 0.275[135，145) 4 ③[145，155] 0.050合计 ④

(1)根据上面图表，求出①②③④处应填的数值;

(2)在所给的坐标系中画出[85，155]的频率分布直方图及折线图;

(3)根据题中信息估计总体平均数，并估计总体落在[129，155]中的频率.

21.(12分)学习成绩与学习时间存在相关关系，一定条件下，学习时间越长，学习成绩越好.为研究学习成绩与时间的关系，某校高一数学研究小组通过调查研究得到某班8位同学学习时间和数学成绩的相关数据，并根据以上数据，绘制了散点图.

时间x/h 0.1 0.3 0.5 1 1.5 2 2.5 3数学成绩y/分55 72 73 69 75 78 81 80.5

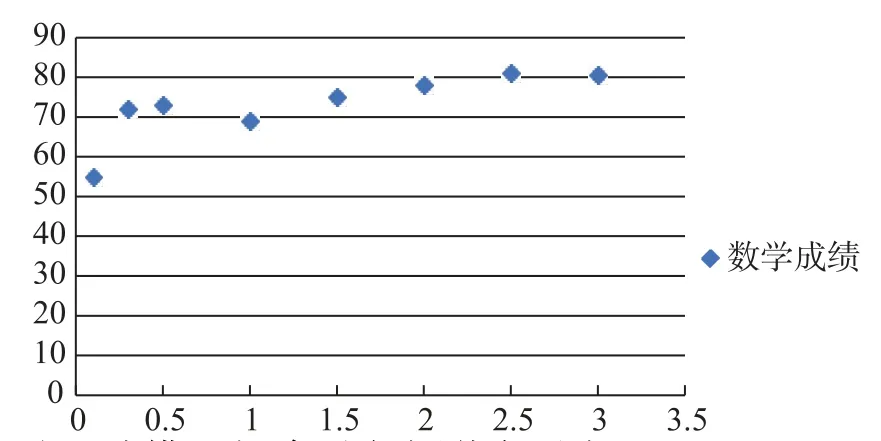
观察散点图，现考虑用线性模型y＝bx＋a或对数函数模型y＝clnx＋d分别对两个变量的关系进行拟合.已求得用线性模型拟合的回归方程为^y＝6.2611^x＋64.407，相关系数r1＝0.7997.

(1)求用对数函数模型y＝clnx＋d拟合的相关系数，并由此对两种模型拟合进行评价与选择.

(2)根据(1)的选择结果，求回归方程.

∑8 i＝1uiyi ¯u ¯u2∑8 i＝1u2 i ∑8 i＝1yi ∑8 i＝1y2 i 490.22×9.776－16.7948－0.1358 0.01842 9.93862 583.5 43049.2 0.6923

其中ui＝lnxi.

22.(12分)在某电信部门执行的新的电话收费标准中，本地网营业区内的通话费标准:前3分钟为0.2元(不足3分钟按3分钟计算)，以后的每分钟收0.10元(不足1分钟按1分钟计算).在一次实习作业中，某同学调查了A，B，C，D，E五人某天拨打的本地网营业区内的电话通话时间情况，其原始数据如下表所示.

A B C D E第一次通话时间 3分 3分45秒 3分55秒 3分20秒 6分第二次通话时间 0分 4分 3分40秒 4分50秒 0分第三次通话时间 0分 0分 5分 2分 0分应缴话费/元

(1)在上表中填写出每人应缴的话费;

(2)设通话时间为t分钟，试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表);

时间段 频数累计 频数 频率 累计频率0＜t≤3 丅 2 0.2 0.2 3＜t≤4 4＜t≤5 5＜t≤6合计 正正

注:累计频率就是样本数据小于某一数值的频率.

(3)若该地网营业区原来执行的电话收费标准是每3分钟为0.20元(不足3分钟按3分钟计算)，问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比，是增多了还是减少了?增或减了多少?