品高考真题 察命题趋势——高考中的二项式定理

颜亚新 张 琥

(1.江苏苏州吴江中学 2.北京外国语大学附属苏州湾外国语学校)

研究高考真题就如同和命题人对话，真题是备考必不可少的参考资料，当我们真正把这些试题研究通透，临考时对试卷就不会有陌生感，并会触类旁通.

从近几年的高考试题来看，二项式定理是高考常考内容，且都是以选择题和填空题的形式出现，侧重考查二项式定理的基础知识和学生的数学运算能力，考查内容主要是求二项展开式的通项、二项式系数和二项展开式中的项的系数等基础问题.

1 核心知识概览

1.1 二项式定理及有关概念

2)二项展开式的通项公式:Tr＋1＝，它表示展开式中的第r＋1项.

1.2 二项式系数的性质

1)对称性:在二项展开式中与首末两端“等距离”的两项的二项式系数相等，即

3)最大值:

a)当n为偶数时，中间一项(第项)的二项式系数最大，最大值为-;

b)当n为奇数时，中间两项项)的二项式系数相等且最大，最大值为

4)二项式系数的和:二项式(a＋b)n展开式的二项式系数和为2n，即奇数项的二项式系数和等于偶数项的二项式系数和，即

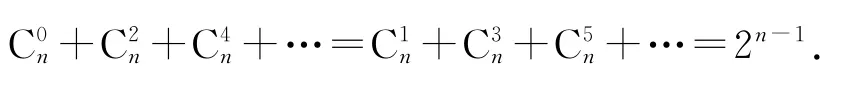
2 高考是怎么考的?

2.1 求二项展开式中的特定项或特定项的系数

对于求特定项或特定项的系数问题，关键是要能灵活运用展开式的通项公式，且要与排列组合知识结合起来，解题时要细心运算.

例1(2021年北京卷11)(x3－的展开式中常数项为_________.

解析

(x3－展开式的通项为

令12－4r＝0，得r＝3，所以常数项为

例2(2021年天津卷11)在的展开式中，x6的 系数是_________(用____数字作答).

解析

(2x3＋)6展开式的第r＋1项为

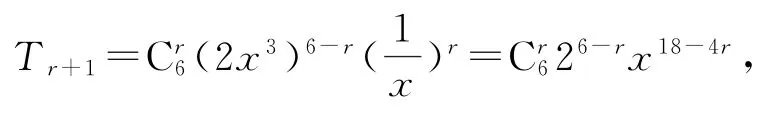
令18－4r＝6，得r＝3，所以

所以x6的系数是160.

例3(2020年全国Ⅲ卷理14)(x2＋)6的展

开式中常数项是(用数字作答).

解析

令12－3r＝0，得r＝4，所以展开式的常数项是×24＝15×16＝240.

点评

求形如(a＋b)n(n∈N*)展开式中的特定项或与其相关的量:第一步，利用二项式定理写出二项展开式的通项Tr＋1＝，通常把字母和系数分开(注意“±”号不要写错);第二步，根据题设条件(如常数项要求指数为零，有理项要求指数为整数等)先列出相应方程(组)或不等式(组)，再求出r的值;第三步，把r的值代入通项中，即可求出Tr＋1＝，有时还需要先求n，再求r，最后求出Tr＋1＝或其他量.

例4(2020年全国Ⅰ卷理8)

的展开式中x3y3的系数为( ).

A.5 B.10 C.15 D.20

解析

因为(x＋y)5展 开 式 的 通 项 为Tr＋1＝

的每一项与(x＋y)5展开式的通项的乘积可表示为

和

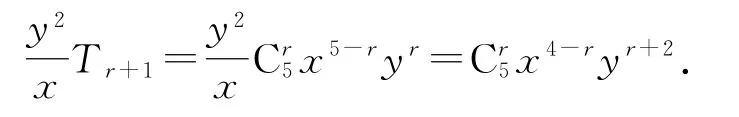
在xTr＋1＝中，令r＝3，可 得xT4＝，该 项 中x3y3的 系 数 为10.在中，令r＝1，可得，该项中x3y3的系数为5，所以x3y3的系数为10＋5＝15.故选C.

例5(2019年全国Ⅲ卷理4)(1＋2x2)(1＋x)4的展开式中x3的系数为( ).

A.12 B.16 C.20 D.24

解析

(1＋x)4展开式中的第r＋1项为Tr＋1＝得T2＝C14x＝4x，所以(1＋2x2)(1＋x)4的展开式中x3的项是1×4x3＋2x2×4x＝12x3，即x3的系数是12，故选A.

点评

求形如(a＋b)m(c＋d)n(m，n∈N*)的展开式中的特定项或其相关的量:第一步，利用二项式定理把(a＋b)m与(c＋d)n分别展开，并写出其通项公式;第二步，根据特定项的次数，分析特定项是由(a＋b)m与(c＋d)n的展开式中哪些项相乘得到的;第三步，把相乘后得到的项合并，即得所求特定项或相关量.

2.2 求三项展开式中的特定项或特定项的系数

例6(2015年全国Ⅰ卷理10)(x2＋x＋y)5的展开式中，x5y2的系数为( ).

A.10 B.20 C.30 D.60

解析

在(x2＋x＋y)5的5个因式中，2个因式中取x2，剩余的3个因式中，1个取x，其余因式取y，故x5y2的系数为＝30.故选C.

例7三项式(x2＋3x＋2)5的展开式中，含x的一次项的系数是_________.

解析

方法1(x2＋3x＋2)5＝[(x2＋2)＋3x]5，

其展开式 的 第r＋1项 为Tr＋1＝Cr5(x2＋2)5－r(3x)r，又(x2＋2)5－r的 第k＋1项 为Tk＋1＝Ck5－r(x2)5－r－k2k，所以

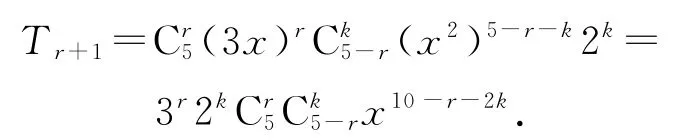
由题意，得10－r－2k＝1，即r＝9－2k，又0≤r≤5，0≤k≤5－r，r∈N*，k∈N*，所以r＝1，k＝故(x2＋3x＋2)5的展开式中，含x的一次项的系数是240.

方法2因 为(x2＋3x＋2)5＝(x＋1)5·展开式中含x的一次项为展开式中含x的一次项的系数是240.

点评

求形如(a＋b＋c)n(n∈N*)的展开式中的特定项或其相关的量:如果可以因式分解，则将三项式分解成两个二项式之积的形式，就可以用2.1的方法求解.如果不能进行因式分解，可将三项式分成两组，利用二项式定理展开，再把其中含两项的一组展开，具体步骤:第一步，把三项的和a＋b＋c看成a＋b与c两项的和;第二步，根据二项式定理写出[(a＋b)＋c]n展开式的通项Tr＋1＝Crn(a＋b)n－rcr;第三步，对特定项的次数进行分析，弄清楚特定项是由(a＋b)n－r展开式中哪些项与cr相乘得到的;第四步，把相乘后得到的项合并，即得所求特定项或相关量.此外，还可以用组合知识，把三项式(a＋b＋c)n(n∈N*)看成n个a＋b＋c的积，然后利用组合知识求解.

2.3 二项式系数与二项展开式中项的系数

区别二项式系数与二项展开式中项的系数是解此类题的关键.二项式系数是固定的，仅与展开式的通项有关，而二项展开式中项的系数包含二项式系数，还有“±”号等，特殊情况下，二项式系数与二项展开式中项的系数是相等的.

例8(2021年浙江卷13)已知多项式(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，则a1＝

解析

方法1由题意知，a1就是展开式中x3项的系数，所以a1＝C03(－1)0＋C14＝5.令x＝1，则有1＋a1＋a2＋a3＋a4＝(1－1)3＋(1＋1)4＝16，所以a2＋a3＋a4＝16－5－1＝10.

方法2由杨辉三角可知(x－1)3＝x3－3x2＋3x－1，(x＋1)4＝x4＋4x3＋6x2＋4x＋1，所以由(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，得a1＝1＋4＝5，a2＝－3＋6＝3，a3＝3＋4＝7，a4＝－1＋1＝0，故a2＋a3＋a4＝3＋7＋0＝10.

例9已知二项式(x＋a)5的展开式中，x2的系数为80，则a＝.

解析

设二项式(x＋a)5展开式中的第r＋1项为Tr＋1＝，由已知得5－r＝2，则r＝3，所以＝80，解得a＝2.

点评

对形如(ax＋b)n，(ax2＋bx＋c)m(a，b，c∈R，m，n∈N*)的式子求其展开式中的各项系数之和，常用赋值法，只需令x＝1即可;对形如(ax＋by)n(a，b∈R，n∈N*)的式子求其展开式中的各项系数之和，只需令x＝y＝1即可.同样，求系数之差时，只需根据题设，令x＝1，y＝－1或x＝－1，y＝1即可.具体赋值方法，要根据所求和式或差式的特征找规律进行赋值.

2.4 与二项展开式中的系数有关的最值问题

例10已知(1＋x)n的展开式中，只有x3的系数最大，则(1＋x)n的系数和为________.

解析

例11(2013年全国Ⅰ卷理9)设m为正整数，(x＋y)2m展开式的二项式系数的最大值为a，(x＋y)2m＋1展开式的二项式系数的最大值为b.若13a＝7b，则m＝( ).

A.5 B.6 C.7 D.8

解析

点评

求解二项式系数或展开式中项的系数的最值问题，首先要弄清楚所求的是“展开式中项的系数最大值”还是“二项式系数最大值”.若是求二项式系数的最大值，则根据(a＋b)n中n的奇偶性及二项式系数的性质求解;若是求展开式中项的系数的最大值，设展开式各项的系数分别为A1，A2，A3，…，Ak＋1，且第k项系数最大.在系数均为正值的前提下，求展开式中项的系数的最大值，只需解不等式组即可.

3 今后还可能考什么?

通过对近几年高考试题的分析与研究，我们不难看出，高考中主要考查二项式定理的基础知识和基本运算，没有难题.因为二项式定理的应用比较广泛，今后的高考中除了出现上述列举的常考题型之外，还会用以下形式来考查二项式定理的有关知识.

3.1 二项式定理的逆用

例12

解析

3.2 整除性问题和求余数问题

例13求证:32n＋2－8n－9(n∈N*)能被64整除.

证明32n＋2－8n－9＝(8＋1)n＋1－8n－9＝

因为上式中的各项都含有82，所以32n＋2－8n－9(n∈N*)能被64整除.

例149192除以100的余数为_________;0.9985精确到0.001的近似值为________.

解析

9192＝(90＋1)92＝，前91项均能被100整除，只有末尾两项不能被100整除，8281＝8200＋81，所以9192除以100的余数为81.

3.3 证明不等式

例15当n∈N*时，求证

证明，又因为

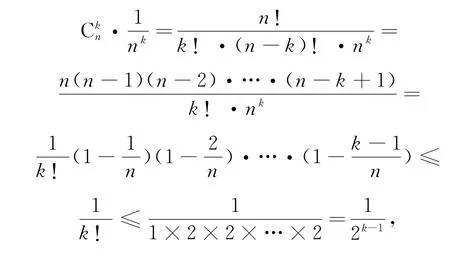
4 我们备考练什么?

练习1在()n的展开式中，各项系数之和为A，各项二项式系数之和为B，且A＋B＝72，则展开式中常数项为_________.

解析

练习2已知(2＋mx)(1＋x)3的展开式中x3的系数为5，则m＝_________.

解析

依题意可知，展开式中x3的项为，所以2＋3m＝5，解得m＝1.

练习3已知(1＋2x)n的展开式中，第6项与第7项的系数相等，则展开式中二项式系数最大的项是_______;系数最大的项是_________.

解析

因为T6＝C5n(2x)5，T7＝C6n(2x)6，由题意得，解得n＝8，所以(1＋2x)8的展开式中，二项式系数最大的项是T5＝C48(2x)4＝1120x4.

设(1＋2x)8展开式第r＋1项的系数最大，则

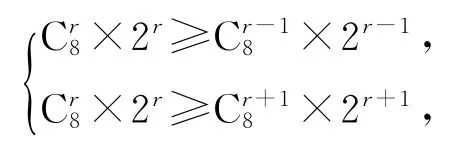
解得5≤r≤6.

又因为0≤r≤8，且r∈N，所以r＝5或6，所以(1＋2x)8展开式中系数最大的项是T6＝C58(2x)5＝1792x5或T7＝C68(2x)6＝1792x6.

练习4若n∈Z，且3≤n≤6，则的展开式中的常数项为_________.

解析

练习5已知f(x)＝(1－x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则(a0＋a2＋a4)(a1＋a3＋a5)的值为________.

解析

因为f(1)＝a0＋a1＋a2＋a3＋a4＋a5＝0，f(－1)＝a0－a1＋a2－a3＋a4－a5＝25，所以

故(a0＋a2＋a4)(a1＋a3＋a5)＝24×(－24)＝－28.