计数原理章节小测
张 琥
(北京外国语大学附属苏州湾外国语学校)
(本试卷共20小题,满分150分,考试用时12分钟)
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.风雨苍黄百年路,高歌奋进新征程.时值建党100周年,为深入开展党史学习教育,某街道党支部决定将4名党员安排到3个社区进行专题宣讲,且每个社区至少安排1名党员,则不同的安排方法总数为( ).
A.12 B.24 C.36 D.72
A.28 B.-28 C.56 D.-56
3.车马理论也称霍姆斯马车理论,是指各种资源都得到最合理配置和使用充分均匀的一种理论.管理学家经常将“霍姆斯马车理论”引申:一架完美的马车,没有最好的部件,只有最完美、最平衡的组合.一个富有效率的团队,不需要每个人都是最有能力的,而在于每个人的能力都能得到最合理的使用和发挥.某班一小队共10名同学,编号分别为1,2,…,9,10,要均分成两个学习小组(学习小组没有区别),其中1,2号同学必须组合在一起,3,4号同学必须组合在一起,其余同学可以随意搭配,就能达到最佳效果,那么共有( )种不同的分组方式.
A.26 B.46 C.52 D.126
4.(x2+2x+y)5的展开式中,x5y2的系数为( ).
A.60 B.30 C.15 D.12
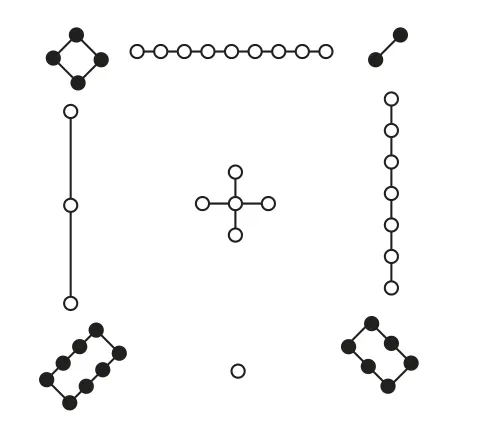
5.如图,洛书(古称龟书)是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.若从四个阴数和五个阳数中随机选取3个数,则选取的3个数之和为奇数的方法数为( ).
A.30 B.40 C.42 D.44
6.已知正整数n≥7,若的展开式中不含x5的项,则n的值为( ).
A.7 B.8 C.9 D.10
7.若x6=a0+a1(x+1)+a2(x+1)2+a3(x+1)3+…+a6(x+1)6,则a3=( ).
A.20 B.-20 C.15 D.-15
8.2020年是实施脱贫攻坚的最后一年,某地区针对最后深度贫困的A,B,C,D,E五个自然村引入五个脱贫项目(其中林果、茶园、养殖、旅游、农业特色深加工各一个项目)进行对口帮扶,不同的村安排不同的项目,且每个村只安排一个项目.由于自然村条件限制,A,B两个村无法实施农业特色深加工项目,C村无法实施养殖项目,D,E两个村可以实施任何项目,则符合条件的不同安排方式共有( ).
A.48种 B.54种 C.60种 D.72种
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得2分.)
9.下列结论中,正确的有( ).
A.所有元素完全相同的两个排列为相同排列
B.两个组合相同的充要条件是其中的元素完全相同
C.若Cxn=Cmn,则x=m
D.排列的定义规定,给出的n个元素各不相同,并且只研究被取出的元素也各不相同的情况,即如果某个元素已被取出,则这个元素就不再取了
A.存在n∈N*,展开式中有常数项 B.对任意n∈N*,展开式中没有常数项
C.对任意n∈N*,展开式中没有含x的一次项 D.存在n∈N*,展开式中含有x的一次项
11.从6名男生和4名女生中选出4人去参加一项创新大赛,则下列说法正确的有( ).
A.如果参加的4人中男、女生各有2人,那么共有30种不同的选法
B.如果男生中的甲和女生中的乙必须参加,那么共有28种不同的选法
C.如果男生中的甲和女生中的乙至少有1人参加,那么共有140种不同的选法
D.如果参加的4人中必须既有男生又有女生,那么共有184种不同的选法
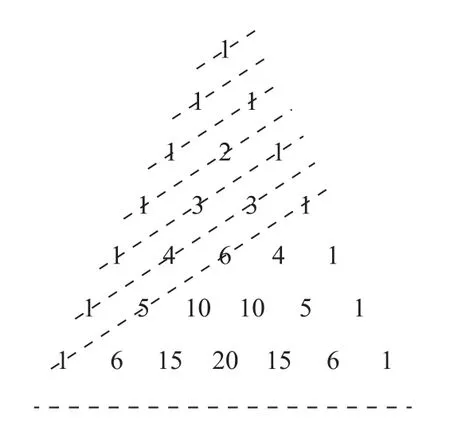
12.“杨辉三角”是中国古代数学杰出的研究成果之一.如图所示,从“杨辉三角”的左腰上的各数出发,引一组平行线,从上往下每条线上各数之和依次为1,1,2,3,5,8,13,…,则( ).
A.在第9条斜线上,各数之和为55
B.在第n(n≥5)条斜线上,各数自左往右先增大后减小
C.在第n条斜线上,共有个数
三、填空题(本题共6小题,每小题5分,共30分.)
14.6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排3名,乙场馆安排1名,丙场馆安排2名,则不同的安排方法共有_________种(用数字表示).
15.现有标号为①,②,③,④,⑤的5件不同新产品,要放到三个不同的机构进行测试,每件产品只能放到一个机构里.机构A,B各负责一个产品,机构C负责余下的三个产品,其中产品①不在A机构测试的情况有________种(用数字表示).
17.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2“,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是_________.
18.(1+x)m+(1+3x)n(m,n∈N*)展开式中x的系数为11,当x2的系数取最小值时,x4的系数是_________.
四、解答题(本题共2题,共计60分.解答时应写出文字说明、证明过程或演算步骤.)
19.(30分)男运动员6名,女运动员4名,其中男、女队长各1名,现选派5人外出参加比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名; (2)至少有1名女运动员;
(3)队长中至少有1人参加; (4)既要有队长,又要有女运动员.
20.(30分)已知(3x2+3x2)n展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.

