谈构造递推关系式法在计数问题中的应用

刘海涛

(安徽省芜湖市第一中学)

《中国高考评价体系》指出:高考要从“知识立意”转向“能力立意”，考查学生的“关键能力”和“核心素养”.这就要求学生在学习中学会灵活运用所学知识分析、解决问题，达到从“解题”向“解决问题”的转变.解答一些看似与数列无关的计数问题时，若我们深入剖析问题，利用类比联想、抽象转化，通过建立数列的递推关系模型表示计数规则，则可将问题转化为数列问题，避免繁杂的分类讨论，简化解题过程，同时可将问题拓展到一般化模型.

1 涂色问题

例1如图1所示，用四种不同的颜色给六边形ABCDEF的六个顶点涂色，若相邻顶点不同色，则不同的涂色方案共有_________种.

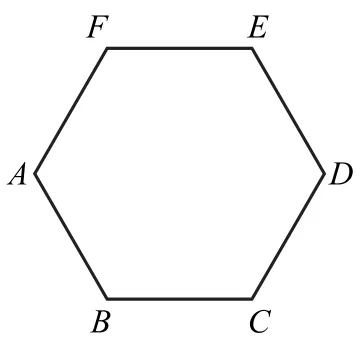
图1

解析

用四种颜色给n边形A1A2…An的顶点涂色，相邻顶点不同色，不同的涂色方案数记作an(n≥2).从n－1边 形A1A2…An－1到n边 形A1A2…An，我们考虑增加的顶点An的涂色问题.

若A1与An－1同色(n≥4)，则An有三种颜色可供选择，而前n－2个顶点满足相邻不同色，所以此时有3an－2种方案.

若A1与An－1不同色，则An有两种颜色可供选择，而前n－1个顶点满足相邻不同色，所以此时有2an－1种方案.

综上，得到递推关系式an＝2an－1＋3an－2(n≥4)，易知a2＝A24＝12，a3＝A34＝24，经计算得a6＝732，所以有732种涂色方案.点评

本题只有六个顶点，利用分类讨论的思想逐一分析可以快速解题，但是若点数较多，则分类情况太多，难以求解.从n－1边形到n边形增加的顶点的涂色情况分析，可以建立递推关系式顺利解题，同时可将问题拓展为一般化模型.

模型1用m(n≥m≥3)种不同的颜色给n(n≥3)边形A1A2…An的n个顶点涂色，若相邻顶点不同色，则不同的涂色方案共有(m－1)n＋(－1)n(m－1)种.

证明n边形A1A2…An不同的涂色方案数记作an(n≥3).若A1与An－1同色(n≥4)，则An有m－1种颜色可供选择，而前n－2个顶点满足相邻不同色，所以此时有(m－1)an－2种方案.若A1与An－1不同色，则An有两种颜色可供选择，而前n－1个顶点满足相邻不同色，所以此时有(m－2)an－1种方案.

综上，得到递推关系式an＝(m－2)an－1＋(m－1)an－2(n≥4)，易知a2＝A2m，a3＝A3m.解特征方程x2＝(m－2)x＋m－1，得特征根为m－1和－1，设an＝λ·(m－1)n－1＋μ·(－1)n－1，则于是an＝(m－1)n＋(－1)n(m－1)，不同的涂色方案共有(m－1)n＋(－1)n(m－1)种.

2 登台阶问题

例2现要登一个十级的台阶，每一次可登一级或两级，则有多少种不同的登法?

解析

不妨将n级台阶的登法数记作an，因为登到第n级台阶的方式有两种:一种方式是从第n－2级台阶直接登上第n级台阶，另一种方式是从第n－1级台阶登上第n级台阶，所以得到递推关系式an＝an－2＋an－1(n≥3)，易知a1＝1，a2＝2，经计算得a10＝89，所以共有89种登法.

点评

模型2登上一个n级的台阶，若每一次可登一级或两级，则有种登法.

证明登上n级台阶的登法数实为数列{an}的通项，而 数列{an}满 足:a1＝1，a2＝2，an＝an－2＋an－1(n≥3).解 特 征 方 程x2＝x＋1，得 特 征 根 为

3 全错位排列问题

例3现有分别标号为1，2，3，4，5的五个球与五个盒子，将五个球分别放入五个盒子中，每个盒子仅一个球，若要求球的编号与所在盒子的编号均不同，则有多少种不同的放球方法?

解析

不妨把编号为1，2，…，n的球放入编号为1，2，…，n的盒子，符合题设条件的放法数记作an.我们分两步来完成放球:第一步，将标号为n的球放到标号为m的盒子里，有n－1种放法.第二步，考虑编号为m的球，有两种放法，即放到编号为n的盒子里，则余下n－2个球放到n－2个盒子，有an－2种放法;不放到编号为n的盒子里，这时对于这n－1个球，共有an－1种放法.

综上，得到递推关系式an＝(n－1)(an－2＋an－1)(n≥3)，易得a1＝0，a2＝1，经计算a5＝44，所以共有44种放法.

点评

由滁州市统计局网站公布的信息可知，2018年上半年全市地区生产总值增长9.7%，高于全省增速1.4个百分点，高于预期增速2.1个百分点，高于同期增速0.5个百分点。市场消费增长，网上零售发展较快，城乡协调发展，商品零售和餐饮消费协调发展。就业形势良好，物价保持稳定，居民收入稳步增长。从企业的经营情况和财政收入结构看，经济发展的质量效益不断提高。工业增速回升，在全省的位次较高，国有企业、园区工业增长加快，部分行业贡献较大，亿元企业的拉动力较强。高新、战略新兴产业取得较快增长，创新创业成效明显，产业转型升级稳步推进。

本题实际上是组合数学中的错排问题，就是将n个元素进行排列，若每一个元素均不在原来的位置，则称之为这n个元素的一个错排.根据解答不难发现，可建立数列模型求解错排问题.

模型3若将n个元素进行排列，使得每一元素均不在原来位置，则共有n!种排列方法.

证明n个元素的错排方法数为数列{an}的通项，而 数 列{an}满 足:a1＝0，a2＝1，an＝(n－1)·(an－2＋an－1)(n≥3).

由an＝(n－1)(an－2＋an－1)，得an－nan－1＝－[an－1－(n－1)an－2]，则{an＋1－(n＋1)an}是以a2－2a1＝1为首项，－1为公比的等比数列，则

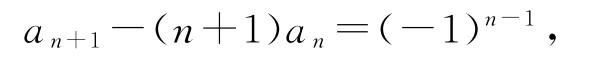
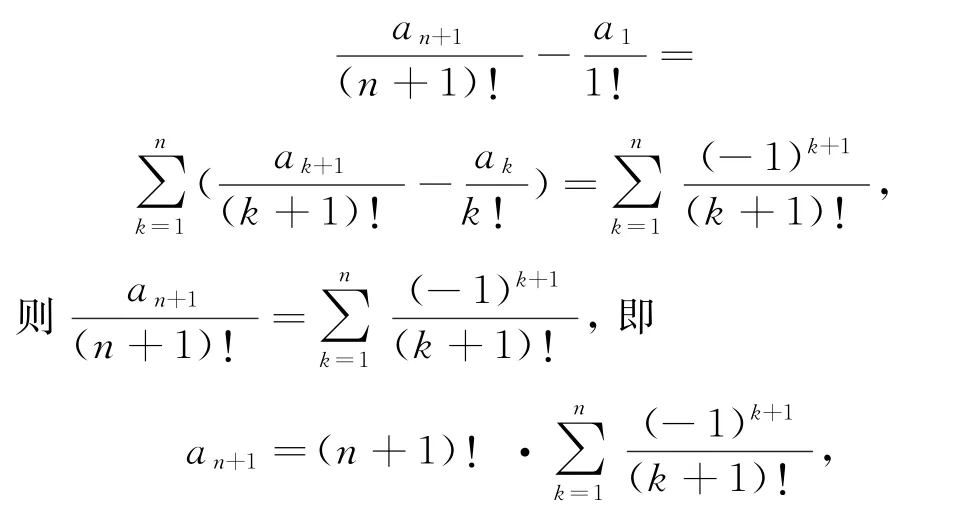
4 有序子集对问题

例4已知集合M＝{1，2，…，5}，P，Q为M的两个非空子集，若子集P的最小元素大于子集Q的最大元素，则有多少对有序子集对(P，Q)?

解析

设集合Mn＝{1，2，…，n}，对应符合题设条件的有序子集对个数记作an，从集合Mn－1到Mn，我们只需要考虑多出的元素n，显然元素n只能属于子集P.

若元素n放入或不放入集合Mn－1对应的子集P，都能保证集合Mn－1对应的有序子集对(P，Q)满足集合Mn，则有2an－1对.

若元素n单独构成集合P＝{n}，则Mn－1的任一非空子集都可作为子集Q，构成满足集合Mn的有序子集对，有2n－1－1对.

综上，得到递推关系式an＝2an－1＋2n－1－1(n≥2).易知a1＝0，a2＝1，经计算得a5＝49，所以共有49对有序子集对(P，Q).

点评

若直接讨论求解本题，情况较多，容易遗漏，且过程复杂，不易得到正确结果，而从子集元素个数的角度入手，抓住从集合Mn－1到Mn的变化情况，建立起相应的递推关系式，就可轻松解题.另外，由解答过程我们不难将问题拓展为一般模型.

模型4已知集合M＝{1，2，…，n}，P，Q为M的两个非空子集，若子集P的最小元素大于子集Q的最 大 元 素，则 有(n－2)2n－1＋1对 有 序 子 集对(P，Q).

证明有序子集对(P，Q)的个数实为数列{an}的通项，而数列{an}满足:a1＝0，an＝2an－1＋2n－1－1(n≥2).由an＝2an－1＋2n－1－1，得

5 传球问题

例5三个人互相传球，由甲开始发球，并作为第一次传球，经过5次传球后，球仍回到甲手中，则有多少种不同的传球方式?

解析

设第n次将球传给甲的方式有an种，传n次球共有2n种不同的传法，在这2n种传法中，有2n－an种传法第n次不是传给甲，而第n次没有传给甲时，在第n＋1次传球时可传给甲，故第n＋1次传给甲的传法为an＋1＝2n－an，易知a1＝0，经计算得a5＝10，则经过5次传球后，球仍回到甲手中，有10种不同的传球方式.

点评

该题也可直接列树状图解答，但相对来说较为复杂，若增加传球的次数，则树状图更加繁杂，容易出错，而采用构造递推关系式表达传球次数之间的联系，则可简化解题过程，由此可将问题拓展.

模型5m(m≥2)个人互相传球，甲先发球，并作为第一次传球，经过n次(n≥2)传球后，球仍回到甲手中，则共有种不同的传球方式.

证明设第n次将球传给甲的方式有an种，传n次球共有(m－1)n种不同的传法，在这(m－1)n种传法中，有(m－1)n－an种传法第n次不是传给甲，而第n次没有传给甲时，在第n＋1次传球时可传给甲，故第n＋1次传给甲的传法为an＋1＝(m－1)nan，则

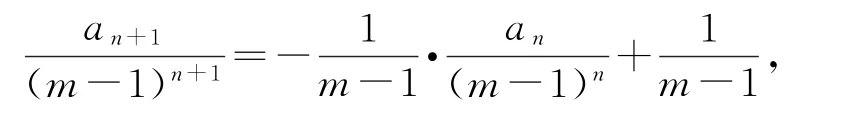
即

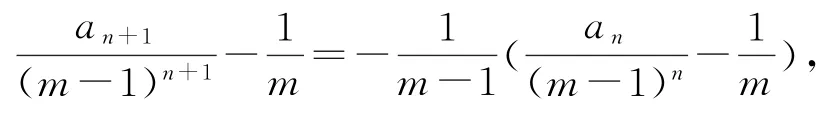
易知a1＝0，则数列为首项，为公比的等比数列，所以

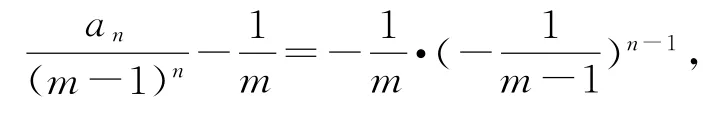
即

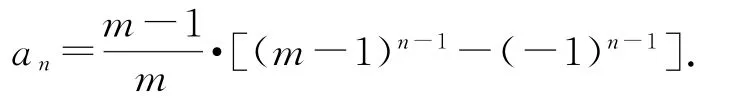
通过以上五道例题，笔者介绍了构造递推关系式来解决五类计数问题，并在此基础上将问题拓展到一般化模型，找到解题规律，简化解题步骤.