平均冲量在解电磁学题目中的妙用

王建国

（甘肃省甘谷县第四中学）

在电磁学问题中，运动的带电体所受到的合力往往不是恒定的，会随着电流或者磁场的变化而呈非线性变化，因此有些问题无法通过直接求值的方法进行分析，这为解题带来了一定困难.然而，学习了冲量后，我们会发现，力的冲量的大小等于力的大小和力的作用时间的乘积，当力变化时，我们可以直接用该变化的力的平均值乘作用时间求得该力的冲量.这一规律为我们打开了一扇解题的便捷之门，在电磁学问题中，它同样适用.在电磁学问题中，我们可先求出一段时间内电路中流过的电荷量q，或者求出研究对象所受安培力的平均冲量，或者通过电路中磁通量的变化量ΔΦ求解.具体思路如下.

思路分析如图1所示，在一水平放置、长度足够长的导轨上，垂直放置一根长为L的金属棒.已知空间内存在一方向垂直轨道平面向上的磁感应强度为B的匀强磁场，金属棒与导轨接触良好组成一回路，且二者间的摩擦力忽略不计、回路电阻为R.当给金属棒一个水平向右的初速度后，金属棒向右运动时间t后停止，回路中的感应电流的平均值为ˉI，通过回路的电荷量为q，回路中磁通量的改变量为ΔΦ，则此过程金属棒所受安培力的平均冲量大小IA＝BˉILt＝BLq.又由

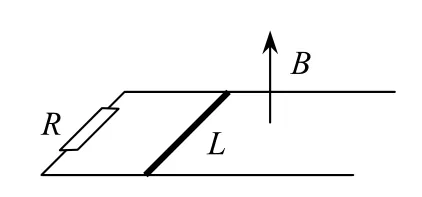
图1

它对解决电磁学问题究竟有什么用呢?下面我.们就用例题来说话.

例1如图2所示，两根电阻不计、长度足够长的光滑金属导轨MN、PQ，用一阻值R＝3Ω的电阻相连，平行固定在水平面上，两根导轨之间的距离L＝0.5m，垂直水平面方向向下有一磁感应强度B＝2T的匀强磁场.现将一阻值r＝1Ω、质量m＝0.2kg的金属细杆垂直导轨跨接在导轨之上，用水平向右的力F＝2N拉动金属细杆使其由静止开始运动.问：

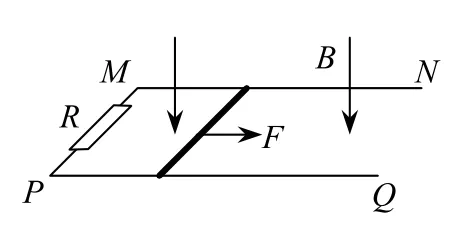
图2

(1)金属细杆能达到的最大速度vm有多大?

(2)在金属细杆从速度为0至达到最大速度的整个过程中，电阻R产生的热量QR＝10.2J，这个过程持续了多长时间?

(3)在金属细杆达到最大速度时即撤去拉力，金属细杆可在导轨上继续运动的距离为多长?

解析

(1)在水平方向上，金属细杆受拉力F和安培力FA的共同作用，当金属细杆在水平方向上受力平衡即两个力的大小相等、方向相反时，金属细杆达到最大速度，由此可得

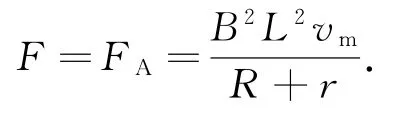
代入数据解得vm＝8m·s－1.

(2)设金属细杆达到最大速度时运动时间为t，运动距离为s，金属细杆上产生的热量为Qr，金属细杆所受安培力的冲量为IA，由系统的功能关系可得

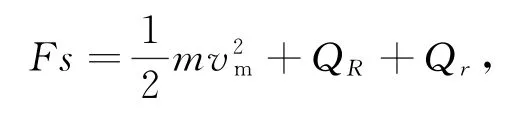
由动量定理可得Ft－IA＝mvm，因此

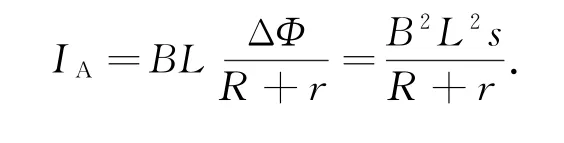
因为金属细杆与电阻R是串联关系，可得解得Qr＝3.4J.

由以上各式及数据可解得t＝2.05s.

(3)设在撤去拉力后金属细杆可在导轨上继续运动的距离为x.当撤去拉力后，金属细杆只受安培力作用，故由动量定理得I′A＝mvm，其中

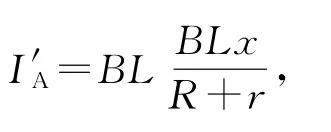
代入可得x＝6.4m.

例2如图3所示，在光滑水平面内有一垂直水平面向下的匀强磁场(磁感应强度为B)，其左右边界平行且清晰.现有一正方形金属框以初速度v0沿光滑水平面向右运动穿过磁场，金属框的边长小于匀强磁场的左右边距，测得金属框完全进入匀强磁场后的速度为v1，完全穿出匀强磁场后的速度为v2，则下列判断正确的是( ).

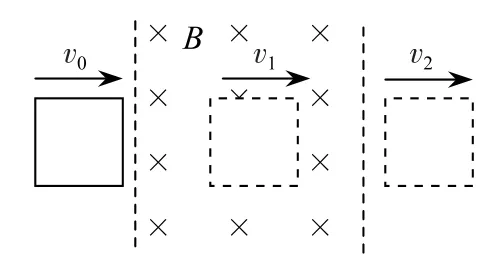
图3

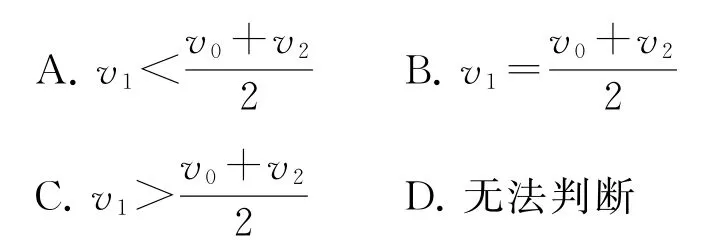
解析

设金属框的边长、质量和电阻分别为l、m、R.在金属框从开始进入到最终穿出匀强磁场的过程中，金属框内的磁通量会产生变化，从而产生感应电流，由楞次定律和安培定则可知金属框做减速运动.当金属框运动速度为v时，其所受安培力显然，其所受安培力与v成线性关系，是一个变力，只有在金属框完全进入匀强磁场的一段时间内其不再受安培力作用，而做匀速运动.金属框进入匀强磁场和穿出匀强磁场的两个过程中，由动量定理得IA1＝mv1－mv0，IA2＝mv2－mv1.这两个过程中，金属框所受安培力的冲量的平均值为即mv1－mv0＝mv2－mv1.故本题正确选项为B.

由以上分析，不难看出，平均冲量虽然是一个很小的知识点，但是在解决一些复杂的变力作用问题时，有着出乎预料的便利效果.而在电磁学问题中，往往因为电流和磁通量的变化，使得受力分析中出现很多变化的力，直接求解就会变得复杂.如果我们换个思路，利用平均冲量的思想来分析问题，就能清晰准确得出结果.