利用“对称性”巧解碰撞问题

李维富

（云南省昭通市第一中学）

碰撞问题是动量守恒定律应用中的经典问题.在求解碰撞后的速度时，如果是完全非弹性碰撞，计算会很简单，但如果是弹性碰撞，涉及二元二次方程组的求解，计算难度比较大.通过分析，可以看出弹性碰撞中蕴含“等差数列”的思想，弹性碰撞是关于共速时刻“对称”的，利用这种“对称性”可以很容易地对碰撞后的速度进行求解，对这种“对称性”进行拓展运用，还可以快速分析其他一些碰撞类问题.

1 问题的引出

例1如图1所示，在光滑水平地面上，质量分别为m1＝3kg、m2＝1kg的A、B两小球分别以速度v1＝10m·s－1、v2＝2m·s－1开始同向运动，发生弹性碰撞，求碰后的速度v′1和v′2.

图1

分析在弹性碰撞过程中，遵循动量守恒定律和机械能守恒定律，所以有

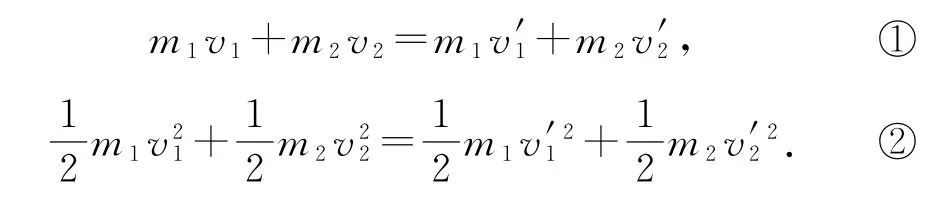
联立上面两式求得

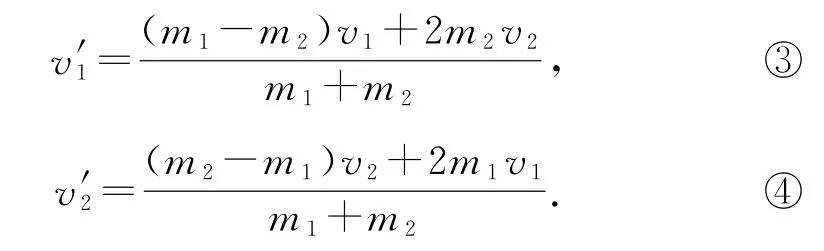
将数据代入式③④可得

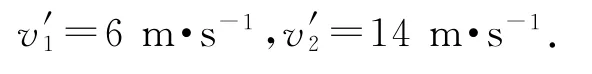
解决上述例题需要学生求解二元二次方程组，比较困难，所以经常要求学生记住③④两式.然而在教学过程中发现，很多学生记不住，即使记住了也很可能混淆.能不能找到一种既不需要记公式又能快速求解的方法呢?答案是“能”.

2 对于弹性碰撞问题的巧妙解答

在图1的碰撞情境中，根据碰撞条件可知，两小球碰撞之前有v1＞v2，碰撞之后有v′1＜v′2，由此可推知在碰撞过程中一定有个时刻两小球速度相等，设为v共.根据碰撞全程动量守恒，可得

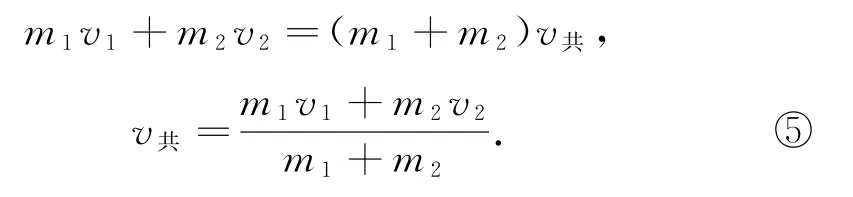
根据数学关系可看出上述的v1、v共、v′1构成等差数列，公差为还可以看出v2、v共、v′2也构成等差数列，公差为.利用这一思想，可以快速计算前面例1中的问题.

由式⑤可以算得v共＝8 m·s－1，再由v1、v共、v′1构成等差数列，可得v′1＝6m·s－1.同理可得

式⑤相比式③、④要好记得多，也可以不用记忆，直接根据动量守恒定律快速求解出v共，然后再利用等差数列的思想快速求解碰后速度v′1和v′2.

3 关于“等差数列”的思考

对于“等差数列”的思想，还可以换个角度来证明.在图1的碰撞情境中，根据弹性碰撞的特点，我们得到了①、②两式.

式①变形可以得到

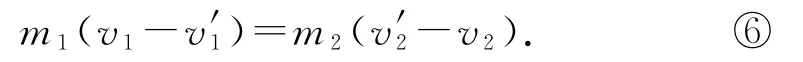
式②变形可以得到

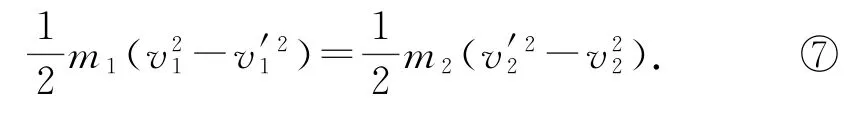
用⑦÷⑥可得到v1＋v′1＝v2＋v′2，或改写成

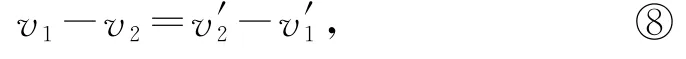
式⑧中v1－v2代表碰前A、B两小球相互靠近的相对速度，v′2－v′1代表碰后两小球逐渐远离的相对速度，二者相等.

在图1的碰撞过程中，因为小球A、B之间的相互作用，A会减速(也可能是减为0后反向加速)，B会加速，可将两球碰撞过程的速度—时间(v-t)图像画出，如图2所示(考虑到两小球并不是做匀变速直线运动，故将之画为虚线).

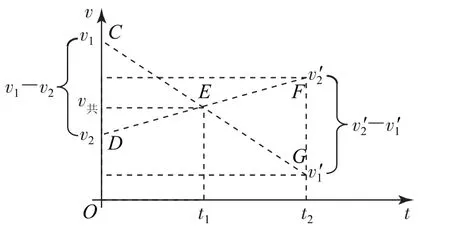
图2

碰撞过程在0～t2这段时间完成.在这段时间内小球A的速度从v1(C点)减为v′1(G点)，小球B的速度从v2(D点)增为v′2(F点)，在碰撞过程中的t1时刻两小球共速(E点).CD段长度代表两小球碰前的相对速度v1－v2，FG段长度代表两小球碰后的相对速度v′2－v′1，前面已经证明二者相等，由此很容易看出△CDE≌△GFE.因为△CDE≌△GFE，故C、G两点关于E点对称，所以v1、v共、v′1构成等差数列；同理，v2、v共、v′2也构成等差数列.

从图2中还可以看出，两小球碰撞过程中共速的时刻t1刚好是整个弹性碰撞全程0～t2时间的中间时刻，弹性碰撞碰前和碰后的速度是关于共速时刻“对称”的.

4 关于“对称性”的拓展应用

我们还可以换个角度来认识碰撞类问题.

从图2可以看出，碰撞不会在t1时刻之前结束，因为在那之前A球速度大于B球速度，与碰撞情境相悖，碰撞可能结束的时刻t应满足t1≤t≤t2.

若碰撞在t1时刻就结束，那就是完全非弹性碰撞，碰后两小球共速，相对速度为0.

若碰撞在t2时刻结束，那就是弹性碰撞，碰后两小球相对速度(A对B)等于碰前相对速度(B对A).

若碰撞在t1～t2之间的某个时刻结束，则是一般的非弹性碰撞，这时A球速度还未减到v′1，B球速度还未增到v′2，两小球的相对速度小于v′2－v′1，也就是小于碰前的相对速度.

综上分析可知，无论什么碰撞，碰后的相对速度不会大于碰前的相对速度.

例2如图3所示，在光滑的水平地面上质量为m的物体A以速度v0与静止的质量为2m的物体B发生碰撞，则碰撞后物体A的速度大小可能是( ).

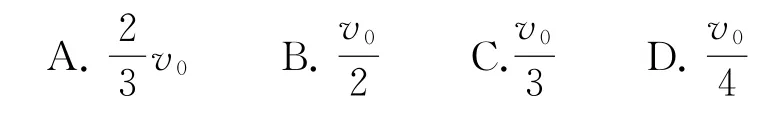
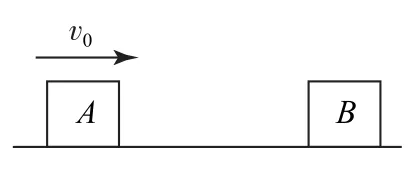
图3

分析本题未说明A、B之间发生什么碰撞，需要分类讨论.若A、B发生完全非弹性碰撞，碰后的共同速度根据动量守恒很容易算出，为若A、B发生弹性碰撞，根据“对称性(等差数列)”的思想可算出碰后A、B的速度分别为.因为碰撞结束时刻只能在t1≤t≤t2范围内，借助v-t图像，可以看出碰后B的速度范围是同时可以看出碰后A的速度大小的范围是的速度范围是，如图4所示，故选C、D.

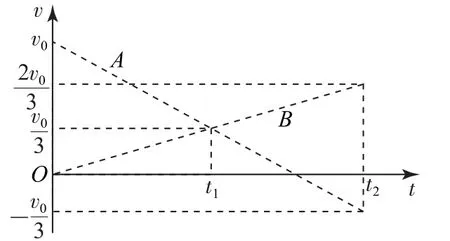
图4

例3如图5所示，质量相等的A、B两球，初始时在光滑水平面上沿同一直线相向做匀速直线运动，A球的速度为6 m·s－1，B球的速度为－2m·s－1，不久A、B两球发生碰撞，对于碰后A、B速度的可能值，不可能的是( ).

图5

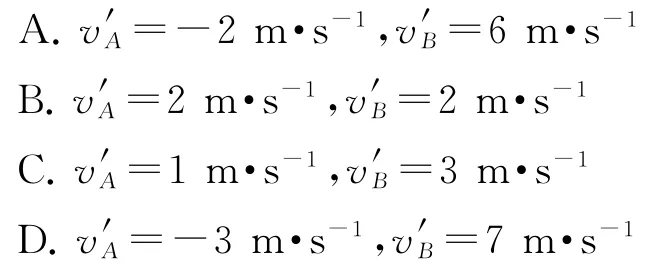
分析本题常见的解题思路是根据碰撞前后系统动量守恒以及碰撞后系统的机械能不大于碰前的机械能联立求解.不过这一思路计算量相对较大，建议用前面的结论去分析，因为碰后的相对速度不会大于碰前的相对速度，所以选D.