铰接式基础风力机数值程序开发与响应研究
章 培, 唐友刚, 杨树耕, 李 焱 , 景雪娇, 尹天畅
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300354; 2.天津大学 港口与海洋工程天津市重点实验室,天津 300354; 3.天津大学 建筑工程学院,天津 300354)
目前,对于水深小于30 m海域,主要采用固定式基础风力机,大于100 m水深海域,采用不同类型的浮式基础风力机。我国海底大陆架不同于欧美国家,地貌相对平坦,当水深超过100 m,离岸距离往往超过50 km,造成铺设电缆及相关配套设施成本急剧加大。而水深大于30 m,固定式风力机建造成本同样显著增加。因此结合我国国情及市场需求,开发一种适用于50 m左右水深的风力基础显得尤为重要。
近年来,国内外研究者针对如何降低风力机水深,提高浅水适用性等开展了相关研究。乐丛欢等[1]提出了一种适用于50 m作业水深的新型全潜式浮式风力机,建立了风力机-塔筒-浮式平台-系泊系统模型,利用FAST软件开展了不同风况下的整体系统动力响应特性研究。邓露等[2]针对中浅水区域提出了钢筋混凝土半潜型浮式风力机平台的概念设计方案,采用SESAM软件进行了水动力特性研究,分析了结构稳定性及整体强度。
基于铰接塔平台及浮式风力机特点,提出了一种铰接式基础风力机(articulated offshore wind turbine,AOWT)结构。对于铰接式基础风力机,目前国内外相关研究还比较缺乏。Njomo等[3]提出了一种适用于中浅水半浮体式铰接风力机方案,采用了有限元软件ABAQUS对结构进行可靠性分析和疲劳载荷计算,并对其作业海况下的摇摆运动进行了数值响应计算。Philip等[4]提出了一种针对5 MW风力机的三腿铰接式基础设计,利用有限元软件NAOS和风力机仿真软件FAST研究了上部风力机结构与铰接基础在风浪流联合作用下的动力响应问题,并开展了不同浪向和风速下的数值计算。
当前针对铰接式风力机的研究,大多集中在结构设计及强度验证等方面。对于动力响应的研究,所选取的作业条件较为简单,作业水深也不适用于我国近海地貌。本文提出了一种新型铰接式基础风力机结构,基于气动力学、水动力学理论,建立铰接式风力机单自由度刚体摇摆运动分析模型,分析其在风、浪、流联合作用下的动力响应特性。
1 铰接式风力机计算模型
本文以NREL 5 WM风力机为研究对象,面向50 m作业水深,对铰接式风力机[5]进行了相应的结构改进和优化,如图1所示。风力机基础塔柱通过铰接接头连接至海底地基,底部设置压载舱以降低结构重心,水线面附近设置浮力舱弥补结构稳性,塔柱高出水面部分留有一定气隙高度并与风力机塔架连接,铰接基础与上部风力机随风浪绕铰接接头做摇摆运动。

图1 新型铰接式基础风力机模型图
1.1 结构模型与参数
铰接式基础整体为分段式立柱结构,为适应水深要求,缩短了中间塔柱尺寸,同时为弥补结构稳性,增大了水线面处浮力舱直径,底部选用半径1.5 m铰接球的接头设计,考虑内部摩擦影响。表1中给出了铰接式基础主要结构的基本参数,其结构形式如图2所示。该基础结构主要由三部分组成:底部设压载舱,高H2=8 m,内部压载混凝土降低结构重心;接近水线面处设浮力舱,高H3=15 m,为整体结构提供回复力;两者间的塔柱高H1=17 m,用于连接上下两个舱体;同时压载舱底部及浮力舱顶部分别留余H1down=2 m及H1up=5 m高度的立柱,保证大角度倾斜条件下,底部压载舱不至于触底撞击,浮力舱不至于浸出水面损失浮力。

表1 铰接式基础结构参数

图2 铰接式基础结构图
本文模型的上部风力机采用美国可再生能源实验室开发的5 MW风力机,其具体参数及风力机整体设计参数如表2所示。

表2 铰接式基础风力机主要设计参数
1.2 分析模型
参考铰接塔平台动力学模型建立铰接式基础风力机的计算模型[6],考虑铰接式基础与上部风力机均为刚体结构,基础塔柱与风力机塔架之间刚性固连,整体结构绕底部铰接接头作单自由度摇摆运动,同时定义铰接点处为系统坐标原点,沿风轮正向为X轴正方向,铰接点至桨毂垂向方向为Y轴方向,本文环境载荷作用主要考虑沿X轴正向方向。
2 计算分析理论
2.1 风载荷
本文主要考虑定常风和湍流风两种特性下的风场情况。定常风状态下,对随高度变化的风速剖面采用风剪切模型进行计算,以风力机轮毂处的风速为依据可得到叶片各叶素处风速。对于湍流风状态下的风场情况,本文采用NPD风谱进行模拟,设计风速u(z,t)按下式进行计算[7]

(1)
式中:Uz为海平面高度z处的1 h平均风速;Iu(z)为湍流强度因子。
(2)
式中,U0为海平面10 m高度处1 h平均风速。
时变风速采用以下谱函数生成
(3)
式中:n=0.468;S(f)为谱密度函数;f为频率。
对于海平面以上高度z处所受湍流风可以归结为设计风速与时变风速的叠加,采用下式进行计算
cos(2π·f·tj+θ)
(4)
式中:θ为随机相位;时间t模拟3 600 s;z=90 m轮毂高度处1 h平均风速为11.4 m/s,根据式(1)计算得到轮毂处设计风速幅值,再结合谱密度函数生成时变风速,同时以1 h时变风速为样本,生成数值模拟3 h的时变风速,图3为1 h样本湍流风时历图。

图3 湍流风时间历程图
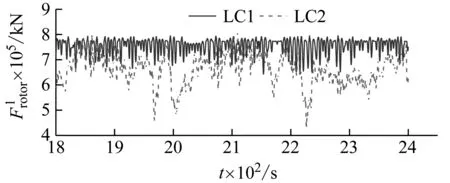
湍流风场中铰接式基础风力机所受风载荷主要分为两部分:风力机叶片轮盘所受气动载荷Frotor及塔架所受风压载荷Ftower。气动载荷基于叶素-动量理论进行求解,将叶片沿展向方向分割为若干小微段,即叶素,采用迭代法求解桨叶不同径向控制体处速度诱导因子,得到收敛后的参数值代入到式(5),分别计算每一叶素所受轴向推力和切向力矩,再积分求得整个叶片所受合力Frotor[8]。
(5)
式中:r为局部半径;v0为来流速度,m/s;a为轴向诱导因子;a′为切向诱导因子;ω0为风轮转速;F为普朗特修正因子。
同时考虑到叶片无穷假设、叶尖及轮毂处旋涡脱落所带来的气动误差,计算中采用普朗特损失因子进行修正,如式(6)所示
(6)
式中:ftip为叶尖修正因子;fhub为轮毂修正因子;R为风轮半径;Rhub为轮毂半径,φ为入流角。
塔柱所受风压载荷按照下式进行计算
(7)
式中:j为受风构件编号;Ch为受风构件高度系数;Cs为受风构件形状系数;Ai(α)为风向角为α时第i个构件的在风向上的正投影面积,m2;Vr为受风构件与风的相对速度,m/s。
2.2 流载荷
铰接式基础流载荷受力结构主要考虑为水面以下立柱、浮力舱及压载舱等结构,参照中国船级社规范采用下式求解
(8)
式中:CD为拖曳力系数;ρW为海水密度,kg/m3;A为构件在与流速垂直平面上的投影面积,m2;Vcur为海流速度,m/s。
2.3 铰接接头摩擦力矩
考虑到铰接式风力机底部铰接头内部摩擦作用,根据所选用铰接接头对应尺寸,其摩擦力矩[9]由下式求得
(9)

2.4 频域水动力分析
对于铰接式风力机的波浪载荷,本文采用三维绕射/辐射水动力软件WADAM计算铰接式基础风力机水动力系数,为了模拟铰接接头,在基础底部添加一个张力腿单元,其轴向刚度与基础剩余浮力相比为大量,从而限制铰接式基础海底地基处的位移,图4为水动力计算模型。

图4 水动力计算模型
考虑系统阻尼(包括辐射阻尼、黏性阻尼及铰接接头摩擦阻尼)、静水回复力矩及波浪激励力等,建立线性规则波作用下铰接式风力机单自由度幅频响应运动方程,复数域内表达式为
[-ω2(I+IA(∞))+iω(C1(ω)+C2)+K]×
θ(ω,β)=F(ω,β)
(10)
式中:I为系统转动惯性矩;IA(∞)为频率趋向于无穷大时附加转动惯性矩;C1(ω)、C2为对应为辐射阻尼系数和黏性阻尼系数,其中黏性阻尼无量纲阻尼比取经验值5%;K为系统回复刚度;F(ω,β)为一阶波浪激励力。
2.5 时域运动方程
根据全局坐标系,将频域计算得到的附加转动惯性矩、势流阻尼及一阶传递函数采用卷积积分方法将随频率变化的附加转动惯性矩和势流阻尼转化为迟滞函数,将一阶波浪力传递函数根据波浪频率成分转化为每一时刻步的波浪载荷代入控制方程[10],采用四阶龙格库塔数值方法求解每一时刻步运动,得到时域运动响应
(11)

2.6 数值程序开发与验证
本文基于气动力学、水动力学理论,建立了铰接式基础风力机单自由度刚体摇摆运动分析模型,并以水动力软件WADAM为基础,MATLAB软件为开发环境,开发了适用于铰接式风力机的气动-水动力-结构耦合的数值仿真程序[11],该程序计算流程如图5所示。

图5 铰接式风力机数值计算程序流程图
其中WADAM主要用于频域内铰接式基础的水动力系数计算,包括六自由度的静水力矩阵、附加质量矩阵、势流阻尼矩阵以及一阶波浪传递函数等;阻尼模块主要是用于系统阻尼力的计算,主要分为3个部分:势流阻尼、黏性阻尼及铰接头的摩擦阻尼。数值程序将这些参数通过外部接口编辑入程序中,结合初始生成的风、浪和流等环境参数,代入到耦合动力响应方程中,求解系统重心处的位移和速度,再将得到的结构位移、速度传递到载荷求解模块,计算结构摇摆运动下载荷变化,再将更新后的载荷作为下一时刻步的外载荷施加到系统中,直至模拟时长结束,通过后处理模块对数值结果进行分析。
由于本文所提出的铰接式风力机既不同于一般的漂浮式海上风力机,也不可采用固定式风力机计算方法直接求解。本文基于水动力软件AQWA平台,建立铰接式风力机水动力模型,开展频域内水动力分析计算,并在FAST主输入文件中定义上部风机及伺服控制参数,调用其中的空气动力学模块(AreoDyn)及伺服控制模块(ServoDyn)。利用其二次开发功能,采用Fortran语言在外部作用力User_force64子程序中定义作用在转子上的空气动力载荷,叶片和塔架的弹性响应以及伺服控制等,并利用编译器进行编译,生成动态链接库文件(dll),将全局坐标系下基础重心受到的外部气动荷载传递到 AQWA 主程序,而AQWA主程序的每一步计算,又将t时刻基础重心速度、位移传递到动态链接库,实现结构与载荷的动态求解过程,风轮推力及输出功率对比如图6所示。

图6 不同风速下风轮推力和输出功率
如图6所示,不同风速作用下,数值程序气动模块所计算得到的风轮推力及输出功率与FAST(AreoDyn)模块数值相差不大,风力机气动特性与设计相一致,从而验证了空气动力模块程序的有效性。
对比验证时选用额定风速工况进行分析,同时采用相同的波浪高程(基于JONSWAP谱)、相同的风速时程(基于NPD风谱)和相同的定常流速,得到关于纵摇运动响应对比结果如图7所示。
从图7可以看出,两者纵摇运动幅值与波动结果吻合得很好;此外,从响应谱图中可以看出,峰值变化也趋于一致,从而验证了数值程序的可靠性。

(a)
3 计算结果与分析
3.1 计算海况
考虑风、浪和流载荷共向作业,波浪采用JONSWAP波浪谱生成的随机波来描述,波浪入射方向为沿X轴正向方向,同时模拟定常风和湍流风两种风场环境,湍流风采用NPD风谱进行模拟,取额定风速11.4 m/s所对应的海况进行分析,流考虑为定常流,具体海况参数如表3所示。

表3 计算海况参数
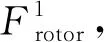

表4 时域响应统计结果
3.2 幅频响应结果分析
依据式(10),计算中考虑系统阻尼(包括辐射阻尼、黏性阻尼和铰接点的结构阻尼)、静水回复力、波浪激励力作用,得到铰接式风力机纵摇方向运动幅值响应算子(response amplitude operator,RAOs),计算结果以0°入射波方向为例给出,如图8所示。
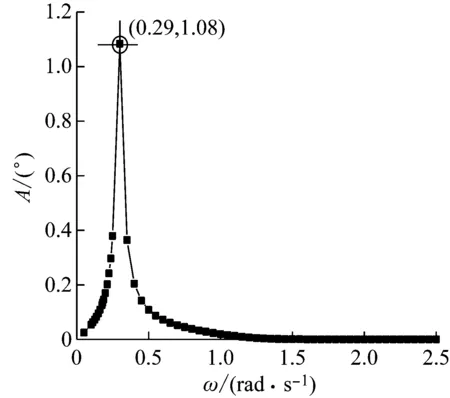
图8 铰接式风力机摇摆运动RAOs
从图8可以看出,系统摇摆运动固有频率约为0.29 rad/s,不在海浪的主要周期范围内,不会引起大幅波频共振;而对于5 MW海上风力机,叶轮转动速率为6.9~12.1 r/min,叶片的1P荷载频率为0.72~1.27 rad/s,3P荷载频率为2.17~3.81 rad/s,系统摇摆运动的固有频率有效避开了风力机叶片转动的1P和3P荷载频率,避免了因叶片旋转而引起的结构内共振,满足结构设计要求。
3.3 湍流风对基础纵摇运动响应分析
图9为基础分别在定常风和湍流风海况下纵摇运动的时间历程曲线及幅值响应谱。

(a)
从图9和表4可以看出,定常风作用下,纵摇响应表现为一个绕平衡位置周期往复的摇摆运动,摇摆幅值在一定有限范围内持续变化,其纵摇运动最大值不超过5°,均值约为4.3°;而湍流风作用下,纵摇运动较定常风幅值变化更加剧烈,标准差明显增大,但整体平均值有所减小,约为3.8°。
从幅值响应谱图中可以看出,定常风作用下,纵摇运动响应谱中主要出现了3个响应峰值,分别对应低于0.3 rad/s的低频响应、0.99 rad/s附近的波频响应及1.27 rad/s的风轮1P响应。当风力机同时受到波浪载荷与气动载荷作用时,由于波谱与1P频率区域重叠,从而引发更多的相互作用和不稳定性[12]。同时由于湍流风的低频特性以及与波浪载荷在低频范围内相互作用诱发低频共振,使得1P频率向低频发生小范围内的偏移,但1P频率及峰值整体变化不大。
3.4 湍流风对风轮推力响应分析
图10为基础分别在定常风和湍流风海况下风轮推力的时间历程曲线及幅值响应谱。
从图10和表4可以看出,定常风作用下,风力机所受风轮推力变化较为平缓,推力值在750 kN附近上下变化,最大不超过800 kN。而受到湍流风作用时,由于时变风速影响,引起风轮诱导速度变化加剧,风轮推力幅值变化显著,标准差增大,同时整体推力均值也显著降低。
(a)
从幅值响应谱图可以看出,推力响应整体表现出与摆角响应类似的峰值变化,定常风作用下,风轮1P频率所对应响应峰值最大,对推力响应起主要作用;而湍流风作用下,在系统低频处诱发较大共振响应,但波频和1P频率处峰值较定常风有所减小。
3.5 湍流风对发电功率响应分析
图11为基础分别在定常风和湍流风海况下发电功率的时间历程曲线及幅值响应谱。

(a)
从图11和表4的结果中可以看出:额定风速定常风海况下,风力机发电功率在5 MW附近上下浮动,表明气动载荷程序模拟效果良好,结构设计满足风力机正常发电需求;而湍流风海况下,发电功率效率显著减低,幅值变化剧烈,发电状态不稳定,同时整体发电功率平均值也大幅降低,约为4.2 MW左右。
从幅值响应谱图中可以看出,较定常风海况,湍流风在低频处诱发较大共振响应,同时波频和1P频率处峰值有所增加,发电功率动力响应整体变化趋势与纵摇响应一致。
3.6 湍流风对铰接点拉力响应分析
图12为底部铰接点合拉力分别在定常风和湍流风海况下时间历程曲线及幅值响应谱。

(a)
从图12和表4可以看出,两种海况下铰接点合拉力值最大不超过50 000 kN,满足铰接接头最大承载力值要求;幅值响应峰值主要集中在波频附近,表明铰接点拉力主要受波浪载荷作用,风载荷对其影响不大,而湍流风与定常风对于铰接点拉力的作用效果有限,两种风场模式下,铰接点拉力响应变化不明显。
4 结 论
本文针对50 m设计水深,提出了一种铰接式基础风力机,基于气动力学、水动力学理论,建立了铰接式风力机单自由度刚体分析模型,开发了计算程序,考虑在额定风速海况下,湍流风与定常风分别对于风力机基础纵摇角,风轮推力、发电功率及铰接点合拉力动力响应的影响规律,得到如下主要结论:
(1) 额定风速海况下,风力机受定常风作用,基础运动性能良好,可以满足正常发电需求,结构设计满足安全服役要求。
(2) 与定常风海况相比,湍流风作用下,基础纵摇运动、所受风轮推力及发电功率平均幅值显著降低,但加大了响应变化的幅度,整体响应更加剧烈;同时在幅值响应谱中,摇摆运动、风轮推力及发电功率响应变化趋势基本保持一致,相比于定常风,湍流风在三者低频范围内诱发了较大的共振,显著提高了低频响应峰值。
(3) 铰接点合拉力主要受波浪载荷影响,风载荷及湍流风对其作用不大。

