基于有限单元和模型降阶的储能飞轮转子动力学建模及分析

周传迪， 柳亦兵， 朱万程， 张昊随

(1．华北电力大学 电站能量传递转化与系统教育部重点实验室，北京 102206；2．华北电力大学 先进飞轮储能技术研究中心，北京 102206)

飞轮储能系统(FESS)具有功率密度大、无污染和充放电速度快等优点，被广泛应用于工程领域。飞轮储能系统的充放电过程通过飞轮转子的升降速实现，转子工作转速宽，但工作转速范围可能包括临界转速，导致振动问题突出[1]，因此有必要对飞轮转子进行动力学建模和分析。

目前，飞轮转子动力学建模方法主要包括有限元法、传递矩阵法及集中质量法。在有限元建模方面，唐长亮等[2-3]建立了飞轮转子的有限元模型，对转子的不平衡响应进行了分析，通过实验验证了计算结果的准确性。在集中质量建模方面，蒋书运等[4]建立了飞轮转子的集中质量模型，采用拉格朗日法得到了转子的运动微分方程并进行了动力学数值仿真。戴兴建等[5]建立了飞轮转子的集中质量模型，分析了飞轮转子的动特性。Wang等[6]建立了四自由度飞轮-阻尼器的集中质量模型，采用拉格朗日法获得了四自由度飞轮的动力学方程，采用有限元法求解挤压油膜阻尼器动态特性的雷诺方程，将计算得到的不平衡响应与试验结果进行对比。Qiu等[7]为100 kg级飞轮储能系统研制了一种摆锤调谐质量阻尼器，利用拉格朗日定理建立了该系统的四自由度动力学模型，从理论和实验上分析了系统的模态特性、临界转速和不平衡响应，并通过实验验证了摆锤调谐质量阻尼器抑制振动的有效性。上述2种建模方法中，有限元法可以得到比较准确的计算结果，但是其计算量较大、计算耗时长；集中质量法将飞轮等效为若干集中质量点，降低了飞轮转子自由度，减少了计算量，但是未考虑转子轮盘厚度的影响，导致分析结果存在误差[8-9]。飞轮转子的半径和转速增加受到材料强度限制，主要通过增加转子轮盘厚度来增加储能，采用集中质量法对转子轮盘厚度较大的飞轮转子进行动力学建模会影响计算结果的准确性。

笔者借鉴集总参数建模方法[10]，综合有限单元法[11]和模型降阶法[12]，考虑转子轮盘厚度，提出一种适用于飞轮转子的建模方法。首先依据集总参数法对飞轮转子进行质量离散化，得到飞轮转子-轴承系统的质量、阻尼和陀螺矩阵以及各轴段的抗弯刚度，然后利用有限单元法计算各轴段的刚度矩阵，再依据飞轮转子刚体假设，采用模型降阶转换矩阵对模型进行简化，得到最终的飞轮转子-轴承系统模型。为验证建模方法的适用性，笔者以飞轮转子-轴承系统为对象，基于Jeffcott转子集中质量建模方法、本文的建模方法以及有限元建模方法进行动特性计算，求解飞轮转子在不同轮盘厚度下的固有频率，对比3种建模方法的计算结果，以有限元模型计算结果作为基准，探究3种建模方法在不同转子轮盘厚度情况下的计算误差，并验证本文建模方法的合理性。

1 飞轮储能系统简介

飞轮储能系统本体部分的主要结构有径向轴承、轴向磁轴承、飞轮转子、电机转子、双向电机及飞轮外壳、抽真空与冷却系统等组成，如图1所示。

图1 飞轮储能系统简化模型

飞轮储能系统通过双向电机对电能与动能进行转换，做到能量的储存和释放。充电时，电能通过电机转换为动能，带动飞轮转子进行升速，直到飞轮转子达到最大工作转速，电机停止驱动，完成充电过程。放电时，飞轮转子的动能通过电机转换为电能进行放电，飞轮转子转速降低，直到降至最小工作转速，此时停止放电，飞轮转子完成放电过程。

飞轮转子-轴承系统是飞轮储能系统的关键子系统之一，为了保证飞轮转子安全稳定运行，有必要对飞轮转子-轴承系统进行动力学建模和动特性分析。

2 飞轮转子-轴承系统建模方法

2.1 基于有限单元法和模型降阶法的飞轮转子-轴承系统动力学建模

由图1可知，飞轮转子-轴承系统主要由转轴、转子轮盘、电机轴套和上下径向轴承组成。为了方便理解笔者提出的基于有限单元法和模型降阶法的飞轮转子动力学建模方法，暂时不考虑电机轴套，对飞轮转子-轴承系统进行简化，如图2所示，其中c1、c2分别为上、下轴承的阻尼，k1、k2分别为上、下轴承的刚度。

图2 飞轮转子-轴承系统简化模型

飞轮转子轴向由永磁轴承支撑，径向由机械轴承支撑，建立动力学模型时不考虑转子轴向振动，并将径向轴承简化为弹簧和阻尼系统。图2中飞轮转子可分为3个轴段：上轴段①，长度为L1；飞轮转子轮盘②，长度为L2；下轴段③，长度为L3。假设飞轮转子有5个节点(图2中节点1～节点5)，上、下轴承分别位于节点1、节点4上。基于以上假设，对飞轮转子进行动力学建模。

根据动力学相关理论，考虑陀螺效应的飞轮转子-轴承系统运动方程的一般形式可以描述为：

(1)

式中：qu为自由度坐标；Mu、Cu、Gu和Ku分别为飞轮转子-轴承系统的质量矩阵、阻尼矩阵、陀螺矩阵和刚度矩阵；Fu为系统所受到的外力和不平衡力；w为转子转速；Mx、My分别为x和y方向的质量；Cx、Cy分别为x和y方向的阻尼；Fux、Fuy分别为x和y方向的外力；qux、quy分别为x和y方向的位移；G、-GT分别为x和y方向的陀螺矩阵。

只要推导出上述各个矩阵的表达式，即可得到完整的飞轮转子-轴承系统动力学方程。

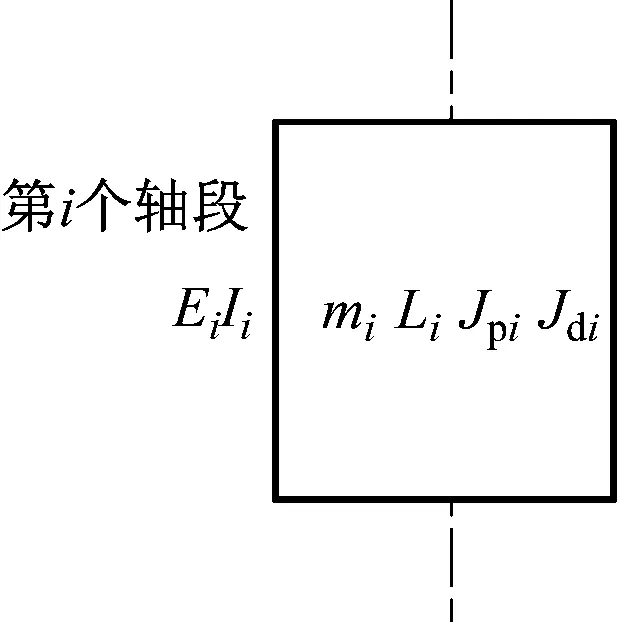
首先，利用集总参数法对飞轮转子进行离散化，如图3所示。将图2中的上轴段①、飞轮转子轮盘轴段②和下轴段③分别标记为i=1、2、3轴段。图3(a)给出了转子的第i个轴段的集中质量模型，其中mi、Li、Jpi、Jdi、EiIi分别为第i个轴段的质量、轴段长度、极转动惯量、赤道转动惯量和抗弯刚度。

考虑转子轴段的质量和刚度，依据质量不变和转动惯量不变原则，将第i个轴段转化为2个有惯性无刚度的集中质量点以及有刚度无质量的弹性轴组成的模型，如图3(b)所示。其中，mi,u、Jpi,u、Jdi,u分别为第i个轴段集中在第i个质量点上的质量、极转动惯量和赤道转动惯量；mi,d、Jpi,d、Jdi,d分别为第i个轴段集中在第i+1个质量点上的质量、极转动惯量和赤道转动惯量。计算公式如下：

(2)

(a) (b)

图2中的转子模型有3个轴段，因此可得到4个集中质量点，将各个轴段集中在各个质量点处的参数相加，可以得到各个质量点处的集总质量和转动惯量。

(3)

不考虑转轴内阻尼，可以得到飞轮转子-轴承系统的质量矩阵Mu、阻尼矩阵Cu和陀螺矩阵Gu的表达式：

(4)

式中：xi为x方向各节点位移；yi为y方向各节点位移；θxi和θyi为转角。

式(4)忽略了自由度θy1、θy4、θx1和θx4，这是因为本文所用轴承为短轴承约束，该转动自由度可由其他自由度表示。

为考虑转子各个轴段的刚度对飞轮转子-轴承系统动特性的影响，采用有限元法，以轴段作为单个单元求解其刚度矩阵。飞轮转子轮盘②可视为无分布力、无约束的梁单元，如图4所示，其中L为梁单元长度，EI为抗弯刚度，M1、M2为两端点的扭矩，F1、F2为两端点的力。上轴段①和下轴段③可视为具有短轴承约束的梁单元，如图5所示，其中kb为轴承约束刚度。

图4 无分布力、无约束梁单元

图5 短轴承支撑梁单元

对于图4所示的无分布力、无约束的梁单元，可根据文献[13]得到其刚度矩阵方程：

(5)

对于图5所示的短轴承支撑的梁单元，可将轴承等效为弹簧刚度[13]，且没有支撑力矩M。因此，短轴承支撑梁单元具有以下边界约束：

(6)

将式(6)代入式(5)可得：

6L·x1+2L2·θy1-6L·x2+4L2·θy2=M2=0

(7)

由于M2=0，自由度θy2可由x1、θy1、x2表示：

(8)

为方便分析，对式(5)进行矩阵分块可得：

(9)

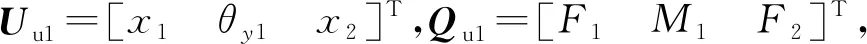
将式(9)化为方程组形式：

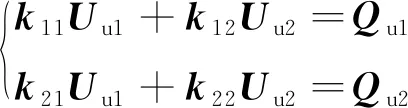
(10)

对式(10)中第2个公式进行分析，得到Uu2与Uu1的关系式：

(11)

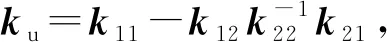
(12)

由此得到下轴段③的刚度矩阵方程为：

(13)

依据F2=-kbx2，将弹簧纳入梁单元中可得：

(14)

综上，上轴段①、飞轮转子轮盘②和下轴段③的刚度矩阵分别为：

(15)

式中：kb1、kb2为上、下轴承约束刚度；I1～I3为3个轴段的转动惯量。

将3个轴段的刚度矩阵置于相应的节点位置并按照有限元法组合得到飞轮转子-轴承系统的刚度矩阵：

(16)

其中，

观察图2转子模型发现，飞轮转子轮盘②的直径与上轴段①和下轴段③的直径相差较大，节点2与节点3之间的刚度较大。为了简化方程，将飞轮转子轮盘②视为刚体，用节点5代替节点2和节点3。假设飞轮转子轮盘②中心节点5的自由度坐标为(x5，y5，θx5，θy5)，依据刚体和小位移假设，得到图2中节点2的自由度(x2，y2，θx2，θy2)和节点3的自由度(x3，y3，θx3，θy3)与(x5，y5，θx5，θy5)的关系：

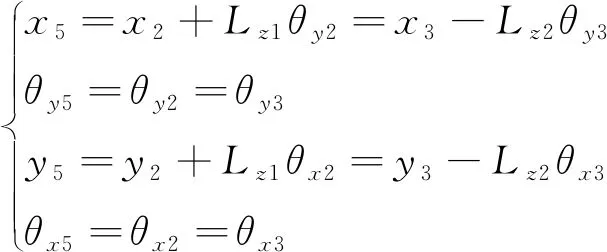
(17)

式中：Lz1和Lz2分别为节点5与节点2和节点3的距离。

根据式(17)，矩阵E1和E2存在以下关系：

(18)

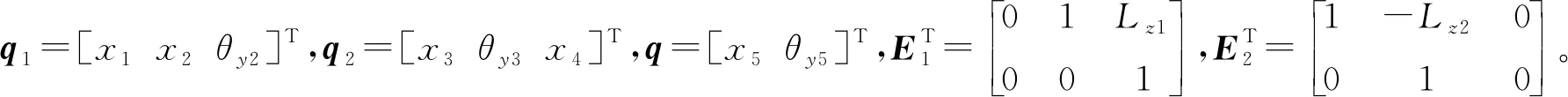
根据式(18)可得：

ETqub=0

(19)

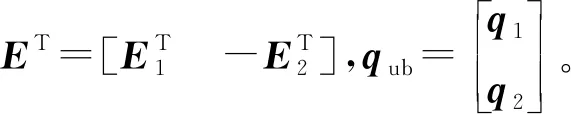
假设存在模型转换矩阵T满足下式：

qub=Tqr

(20)

其中，qr=[x1x5θy5x4]T。

将式(20)代入式(19)可得：

ETqub=ETTqr=0

(21)

由于qr不为零，可得：

ETT=0

(22)

根据文献[13]得到模型转换矩阵T还应该满足矩阵Y1为非奇异矩阵条件：

(23)

经计算得到的模型转换矩阵为：

(24)

其中，

利用模型转换矩阵T对式(1)所示的模型进行模型简化后得到飞轮转子-轴承系统的运动方程：

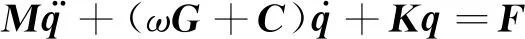
(25)

其中，M=TTMuT,G=TTGuT,C=TTCuT,K=TTKuT,F=TTFu,q=[x1x5θy5x4y1y5θx5y4]T。

2.2 基于Jeffcott转子的集中质量模型

在转子动力学建模方面，基于Jeffcott转子模型的集中质量法应用较为广泛[14-15]。Jeffcott转子模型适用于转子动特性的定性分析，在定量分析方面，其对具有薄轮盘的转子建模误差不大，但是针对储能飞轮转子此类具有厚轮盘的转子，其建模误差较大。

为了探究基于Jeffcott转子模型的飞轮转子在不同轮盘厚度下的建模误差，基于Jeffcott转子模型对飞轮转子进行动力学建模，探讨其建模误差来源，为下文基于该模型的飞轮转子动特性计算和误差对比提供理论参考，仅作为后续章节不同模型之间的计算误差对比之用。

根据Jeffcott转子模型的简化假设，将上轴段①和下轴段③视为有弹性无质量轴，飞轮转子轮盘②简化为一个质量集中在节点5处的圆盘，只考虑飞轮转子的平动自由度(x5，y5)和转动自由度(θx5，θy5)，根据达朗贝尔原理，采用Jeffcott转子模型建立的考虑陀螺效应的飞轮转子-轴承系统的动力学方程[22]如下：

(26)

式中：m为飞轮转子轮盘②的质量；Jd为转子赤道转动惯量；Jp为转子极转动惯量。

式(26)中各个刚度项的计算公式如下：

(27)

式中：a、b分别为飞轮转子中心节点5与上、下轴承的距离。

综上所述，方程式(26)的刚度项来自于轴承弹簧刚度以及上轴段①和下轴段③的抗弯刚度，质量项主要来自飞轮转子轮盘②的质量。因此，Jeffcott转子模型的主要误差来源于忽略转轴质量和忽略转子轮盘厚度产生的刚度影响。

3 建模方法验证

为了探究各建模方法在不同转子轮盘厚度下的误差，对基于Jeffcott转子模型、本文模型及有限元模型建立的飞轮转子动力学模型进行变转子轮盘厚度的固有频率计算，以有限元模型的计算结果作为基准对其他2种模型进行误差分析。

对于实际的飞轮转子系统而言，大多数飞轮转子在转轴上嵌套有电机转子。考虑电机转子质量和附加刚度的影响，建立了如图6所示的飞轮转子-电机转子-轴承系统模型，并计算了在不同转子轮盘厚度下的前两阶固有频率，其中转子轮盘厚度变化范围为25～300 mm，在转子轮盘直径一定的情况下，对应的转子轮盘厚度与直径比为0.08～1，其他参数见表1。

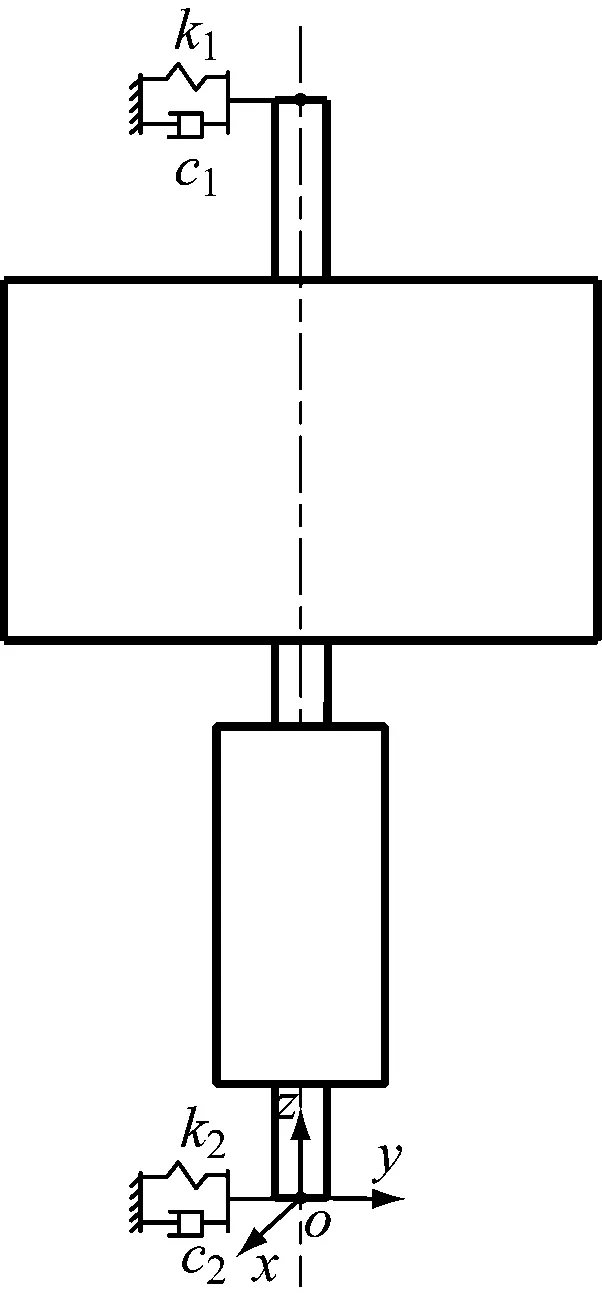
图6 飞轮转子-电机转子-轴承系统模型

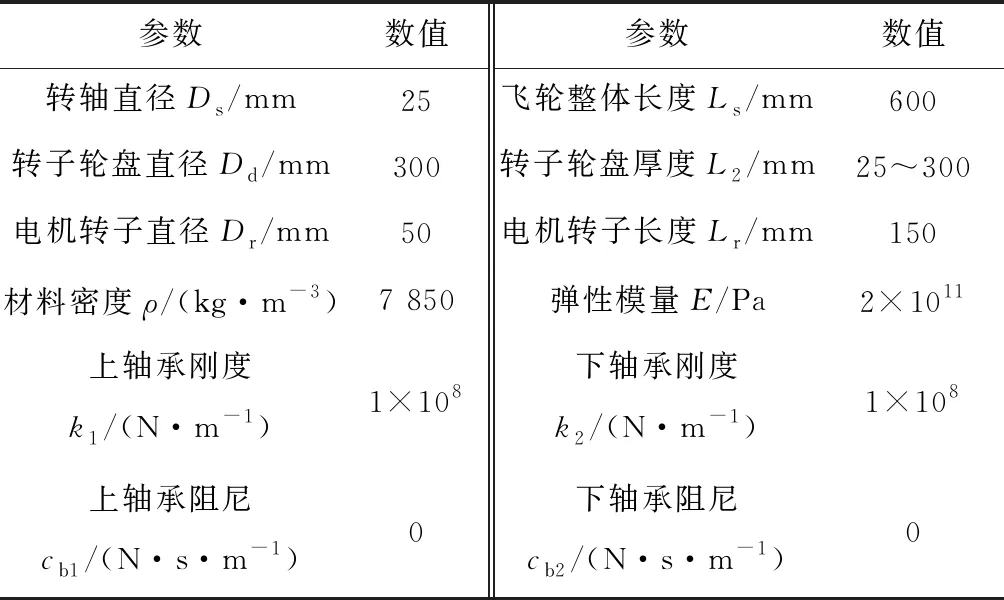
表1 飞轮转子-电机转子-轴承系统参数

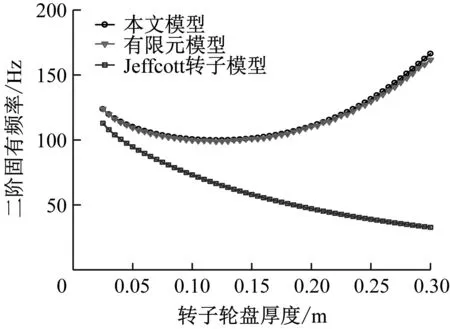
飞轮转子-电机转子-轴承系统的前两阶固有频率随转子轮盘厚度变化曲线如图7所示。对于一阶固有频率，随着转子轮盘厚度增加，本文模型与有限元模型计算结果均呈先减小后增大的趋势，Jeffcott转子模型的计算结果一直呈减小趋势。当转子轮盘厚度较小时，本文模型与有限元模型计算结果有一定误差，随着转子轮盘厚度增加，相对误差逐渐减小。Jeffcott转子模型的计算结果在转子轮盘厚度较小时与有限元模型计算结果接近，随着转子轮盘厚度增加，相对误差逐渐增大。

(a) 一阶固有频率

(b) 二阶固有频率

对于二阶固有频率，随着转子轮盘厚度增加，本文模型与有限元模型计算结果均呈先减小后增大的趋势，Jeffcott转子模型的计算结果一直呈减小趋势。本文模型的计算结果与有限元模型计算结果吻合，当转子轮盘厚度增加至一定值时开始略有差别。Jeffcott转子模型的计算结果与有限元模型计算结果在转子轮盘厚度较小时较为接近，随着转子轮盘厚度增加，两者的相对误差逐渐增大。

Jeffcott转子模型的固有频率ωd与刚度、质量的关系为：

(28)

式中：ks为转子的轴段及支撑的串联刚度；ms为转子的质量，由于Jeffcott转子模型不考虑转子厚度，因此其刚度不随转子轮盘厚度变化而变化，而转子质量随着转子轮盘厚度的增加而增大，从而导致转子的固有频率随转子轮盘厚度的增加一直呈减小趋势。

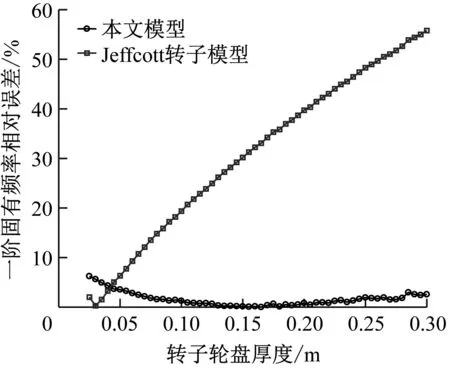
图8为不同转子轮盘厚度下，基于本文模型和Jeffcott转子模型计算得出的飞轮转子-电机转子-轴承系统的前两阶固有频率与有限元模型计算结果的相对误差。从图8可以看出，对于一阶固有频率，Jeffcott转子模型的计算结果在转子轮盘厚度较小时相对误差小，转子轮盘厚度为0.03 m时，相对误差为0.28%，随着转子轮盘厚度的增加，相对误差一直增大，当转子轮盘厚度增加至0.3 m时，相对误差达到最大值55.78%。转子轮盘厚度为0.25 m时，本文模型计算结果的相对误差达到最大值6.24%，随着转子轮盘厚度增加，相对误差逐渐降低，在转子轮盘厚度为0.165 m时相对误差达到最小值0.014%，之后随着转子轮盘厚度进一步增加，相对误差开始逐渐增大，转子轮盘厚度为0.285 m时相对误差增大至2.97%。

(a) 一阶固有频率相对误差

(b) 二阶固有频率相对误差

对于二阶固有频率，Jeffcott转子模型的计算结果相对误差随转子轮盘厚度增加而增大，转子轮盘厚度为0.3 m时，相对误差达到最大值79.77%。本文模型的计算结果相对误差一直较小，转子轮盘厚度为0.3 m时，相对误差达到最大值2.89%。

图9给出了不同转子轮盘厚度与直径比情况下，本文模型和Jeffcott转子模型计算得出的飞轮转子-电机转子-轴承系统的前两阶固有频率与有限元模型计算结果的相对误差。从图9可以看出，基于Jeffcott转子模型的飞轮转子在转子轮盘厚度与直径比为0.08～0.23时，其一阶固有频率相对误差在10%以下；转子轮盘厚度与直径比为0.08～0.12时，二阶固有频率相对误差在10%以下；转子轮盘厚度与直径比为>0.23～1时，相对误差均在10%以上，因此Jeffcott转子模型不适于厚轮盘飞轮转子的动力学建模和动特性计算。

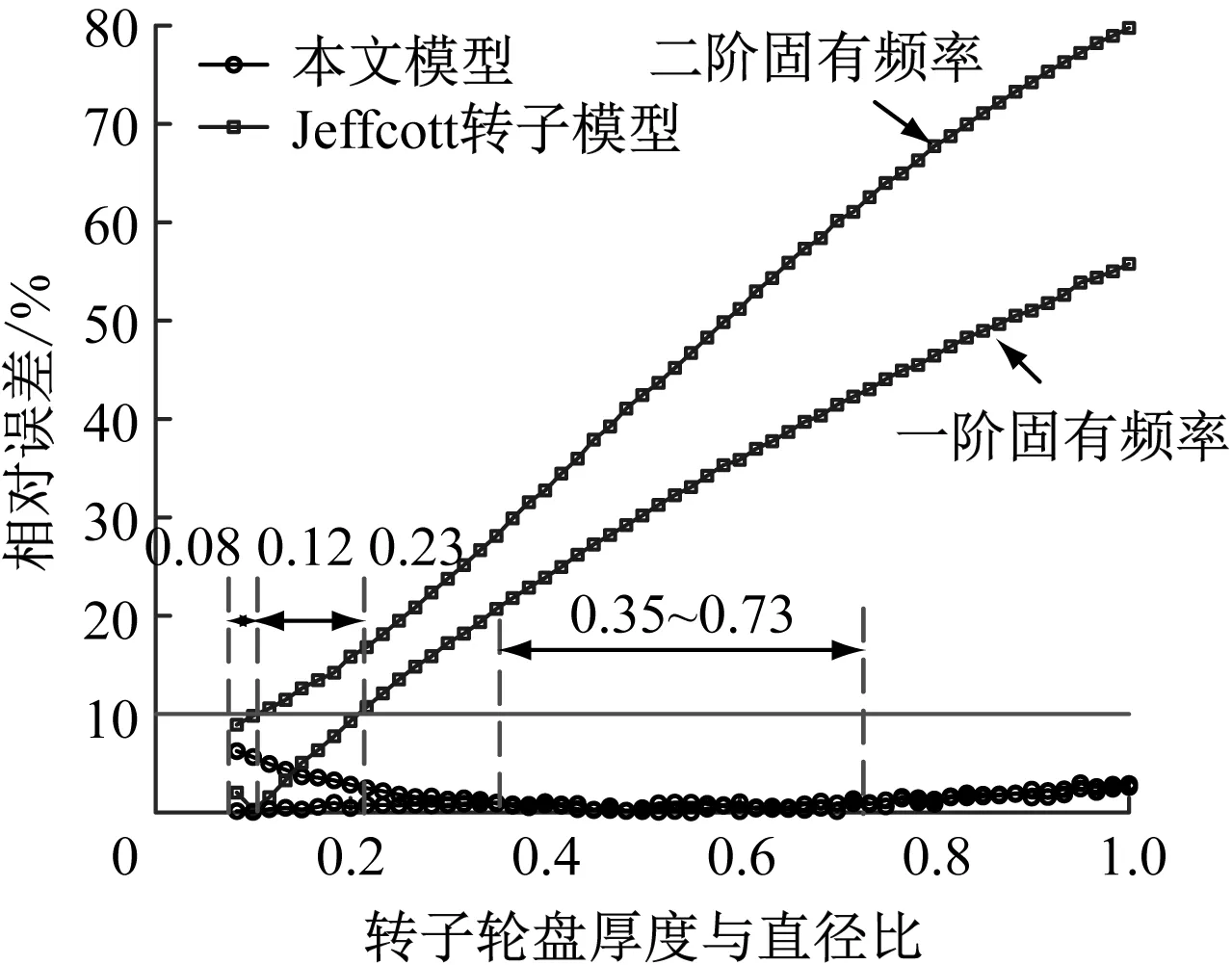
图9 飞轮转子-电机转子-轴承系统的前两阶固有频率相对误差随转子轮盘厚度与直径比的变化

对于本文模型，转子轮盘厚度与直径比为0.35～0.73时，相对误差不超过1%，转子轮盘厚度与直径比在0.08～<0.35、>0.73～1内总体相对误差也较小，最大不超过6.24%，比较适用于厚轮盘飞轮转子的动力学建模和动特性计算。

4 结 论

(1) 当转子轮盘厚度较小，转子轮盘厚度与直径比为0.08～0.23时，3种建模方法计算得到的固有频率相差较小，总体上本文模型与有限元模型的计算结果更为接近。当转子轮盘厚度逐渐增加，转子轮盘厚度与直径比大于0.23时，Jeffcott转子模型的计算结果与有限元模型计算结果的相对误差已超过10%，而本文模型的计算结果则始终与有限元模型计算结果比较吻合，相对误差一直较小，转子轮盘厚度与直径比为0.35～0.73时相对误差最小。

(2) 采用Jeffcott转子模型对转子轮盘厚度与直径比较大的飞轮转子进行动力学建模时相对误差偏大，本文的建模方法对于具有较大轮盘厚度与直径比的飞轮转子动力学建模有较好的适用性。