低压铸造中O形密封圈密封特性分析

冉 迪， 郑 鹏， 王 宁， 卞思文， 韩 志， 王 丹， 王晓凤

(1.沈阳城市建设学院 机械工程学院， 辽宁 沈阳 110167； 2.沈阳工业大学 机械工程学院， 辽宁 沈阳 110870)

引言

低压铸造是在装有金属液的密闭钢包中施加一定的气体压力，金属液通过升液管被压入模具型腔内，保压一定时间后凝固以形成铸件的一种方法。在铸造过程中为确保铸件组织致密，具有较高的力学性能，需要保证包体与包盖间的密封性，而密封性主要取决于密封件的性能。由于低压铸造循环工作周期内， 钢包盖需频繁开启与关闭，铸造设备的密封件基本上采用结构简单，安装方便，密封可靠， 造价低廉的橡胶O形密封圈[1]，而橡胶O形密封圈受材料的限制，温度会对其耐用性、密封可靠性产生极大的影响。根据低压铸造钢包的热分析研究可知，包沿密封处可控温度在163 ℃之下[2]，低压铸造所需气体介质压力在2 MPa内，密封件需在高温极端工况下工作，常出现密封件破损失效问题，最终影响密封性。目前国内外学者对影响橡胶O形密封圈密封性能的各个因素进行了分析[3-8]，但大部分只研究了常温条件下橡胶O形密封圈的磨损、疲劳、应力应变等规律，其中，文献[9]研究了由于气缸与O形圈摩擦生热，O形圈在不同压缩率、滑动速度、介质压力条件下的温度场分布，并未分析在最高摩擦温度50 ℃条件下易失效位置和应力应变等规律。综上，对于160 ℃高温条件下O形密封圈的密封特性的研究很少，因此，本研究采用ANSYS有限元分析软件，对不同温度、压缩率、介质压力条件下的密封性能及密封失效位置进行分析，得出了不同条件下最大Vons Mises应力、最大接触应力的分布现象及规律，为提高密封件的密封性能，降低密封件的破损提供理论与数据依据。

1 O形密封圈计算模型

1.1 O形密封圈材料的本构模型

橡胶材料属于超弹性体，具有高变形度、高弹性、小压缩性，且存在着复杂边界条件和接触非线性等特性，其材料和几何特性均呈非线性变化，所以，对O形圈的有限元分析属于非线性有限元范畴[10]。本研究O形圈材料采用氟橡胶(KFM)，产品的规格为6.99 mm×2160 mm，24 ℃时硬度为75 HB，150 ℃时硬度为65 HB，线性膨胀系数为2.5×10-4℃-1，弹性模量为8.75 MPa，泊松比为0.499，该材料可承受275 ℃ 的高温，具有优越的耐热性和耐腐蚀性。

对于氟橡胶材料应力应变关系，需要使用应变能密度函数来描述，Mooney-Rivlin模型可用来计算不可压缩超弹性橡胶材料在大变形下的力学问题，能够很好地描述变形小于35%的橡胶材料的力学行为[11]，其应变能密度函数为：

(1)

(2)

(3)

(4)

式中，W—— 应变能

C1，C2—— 材料Mooney-Rivlin系数

I1，I2，I3—— 应变不变量，弹性体在长度、表面积、体积上的相对变化

λ1，λ2，λ3—— 主拉伸率

α—— 体积弹性模量

对于不可压缩的超弹性体，I3=1，简化后的应变能函数为：

W=C1(I1-3)+C2(I2-3)

(5)

材料硬度H、弹性模量E与C1，C2的关系为：

(6)

lgE=0.0198H-0.5432

(7)

(8)

计算得出，24 ℃时C1，C2分别为1.166，0.292；150 ℃时C1，C2分别为0.739，0.185。

1.2 有限元模型的建立

1) 模型建立的基本假设

在建立有限元模型时，首先进行了如下假设：

(1) 由于构成密封槽与钢包盖的金属材料泊松比为0.3，弹性模量为206 GPa，远大于橡胶材料的弹性模量，所以不考虑金属变形，即将密封槽与钢包盖视为刚性体；

(2) O形圈及其接触边界按轴对称问题处理，实际上，由于存在加工和装配误差，其结构和受力是不完全轴对称的；

(3) O形圈的泊松比μ=0.499，可视为不可压缩的材料；

(4) 橡胶材料是均匀连续的，没有任何缺陷。

2) 二维有限元模型

采用ANSYS有限元分析软件建立O形圈的二维模型，如图1所示，橡胶单元采用4节点二维实体PLANE182单元，模型中的接触对为面面的刚柔接触，接触对由目标单元TARGE169和接触单元CONTA172组成，按照有限元分析中接触对的定义，将钢包盖、密封槽的底面与侧面作为目标面，O形圈作为接触面，摩擦因数为0.2，采用自由网格划分后，模型共包含1574个节点，1636个单元。本研究采用接触表面法中的增强的拉格朗日法来进行模拟，即为了找到精确的拉格朗日乘子(即接触力)，对罚函数进行一系列的修正迭代，在方程平衡迭代的过程中增大接触附着力(压力和摩擦应力)，以便最终穿透值小于允许的容差值。

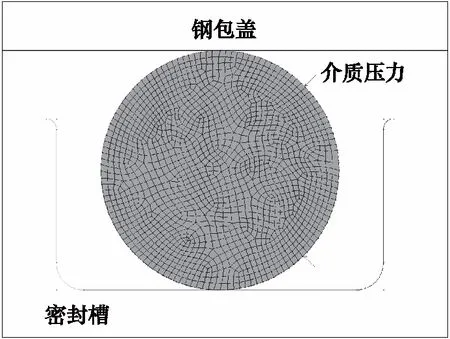
图1 O形密封圈的有限元模型Fig.1 O-ring finite element model

1.3 定义边界与施加载荷

由于O形圈的弹性模量仅为8.75 MPa，密封槽及钢包盖的弹性模量是206 GPa，所以，可以忽略密封槽及钢包盖的变形，将其作为橡胶O形圈的约束边界。

按实际加载顺序，模型中定义了3个载荷步：

(1) 定义节点温度载荷，模拟钢水加入钢包内密封槽温度由24 ℃上升到150 ℃时的温度变化；

(2) 对钢包盖施加向下的位移载荷，数值等于O形圈压缩预紧值，模拟O形圈过盈装配时的压缩率；

(3) 在O形圈右侧边界上施加均布的压力载荷，模拟O形圈所受到的侧向介质压力。

2 工况顺序下的结果与分析

2.1 升温产生的应力分布

Von Mises应力σv反映了3个方向的主应力差值，差值越大的区域不仅容易产生裂纹，还会加速O形圈的应力松弛，降低弹性，使材料产生永久变形，最终导致密封失效；接触应力σc反应了O形圈的密封能力，接触应力越大，密封性能越好，O形圈保证密封的必要条件是密封界面上的最大接触应力大于或等于介质压力[12]。

低压铸造高温钢水使包沿密封处温度升高，经对钢包热分析得出，包沿密封处的温度变化范围为24～163 ℃。如图2所示为无压缩过盈量，无介质压力条件下，仅升温150 ℃后的Vons Mises应力与接触应力。由图2可知，由于包盖约束，O形圈受热膨胀产生了较小形变，温升引起的最大Vons Mises应力σvmax与最大接触应力σcmax分别为0.475 MPa与0.697 MPa，都位于竖向对称轴上，其中，最大Vons Mises应力处于O形圈边缘内侧。

图2 温度为150 ℃条件下的应力分布Fig.2 Stress distribution at 150 ℃

2.2 升温条件下预紧压缩产生的应力分布

图3为当温度T稳定在150 ℃，压缩率ε为15%时的Vons Mises应力与接触应力分布，其中最大Vons Mises应力与最大接触应力分别为1.70 MPa与2.02 MPa，在逐渐施加压缩载荷过程中，O形圈变形量增大，原竖向哑铃状最大Vons Mises应力由密封圈边缘内侧逐渐向中心区贯穿扩展，最后形成规则的矩形；接触应力呈对称抛物线分布，在接触线中点达到最大值，与Hertz接触曲线的分布规律相似。

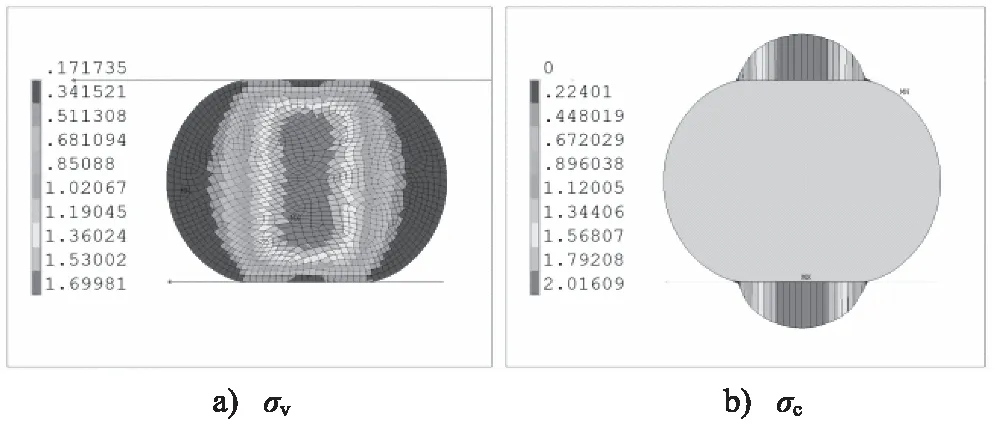
图3 温度150 ℃压缩率15%条件下的应力分布Fig.3 Stress distribution at 150 ℃ and 15% compression

2.3 升温预紧后介质压力产生的应力分布

图4为在温度150 ℃，压缩率为15%条件下，介质压力p为2 MPa时的Vons Mises应力与接触应力分布，其中最大Vons Mises应力与接触应力分别为2.14 MPa 与4.57 MPa。在施加介质压力的过程中，由于边界约束与侧向介质压力的共同作用，最大Vons Mises应力由原规则矩形逐渐分离，并向未加载介质压力方向移动，最终位于O形圈边缘内侧靠近密封槽过渡圆角处，此时O形圈易破损失效位置为边缘内侧密封槽过渡圆附近；上下面最大接触应力由原对称抛物线变为非对称抛物线，密封槽侧壁接触应力呈现准抛物线分布，这是因为介质压力对O形圈有横向挤压，同时介质压力沿上、下密封缝隙渗透，对O形圈竖向有挤压力，导致O形圈上下表面右半侧接触压力减小，左半侧接触应力增加，此时，O形圈的主要密封面为上下接触面左侧，根据密封的必要条件，接触面上的最大接触压力大于或等于介质压力，O形圈具有较好的密封效果。

图4 温度150 ℃、压缩率15%、介质压力2 MPa条件下的应力分布Fig.4 Stress distribution at 150 ℃, 15% compression and 2 MPa pressure

3 不同加载参数下的密封特性

3.1 不同温度下密封特性

为了更好的说明温度变化对O形圈密封特性的影响，图5为压缩率15%、介质压力2 MPa、不同温度条件下O形圈的最大Von Mises应力、最大接触应力曲线。如图5所示，随着温度上升，最大应力均有一定增加，其中，当温度高于180 ℃时，最大Von Mises应力与最大接触应力明显增加，最大Von Mises应力位置和形状也有一定改变。

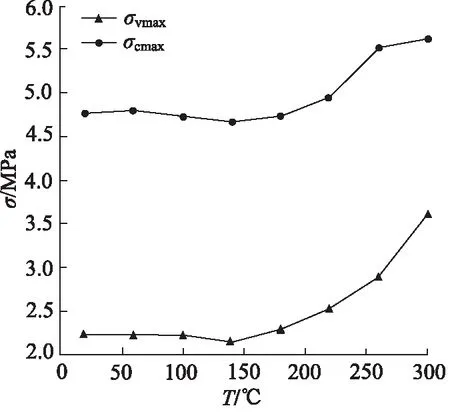
图5 不同温度条件下应力变化趋势Fig.5 Stress variation trend at different temperature

图6为压缩率15%、介质压力2 MPa条件下，温度在20， 140， 260 ℃时最大Von Mises应力变化，随着温度升高，最大Von Mises应力由O形圈竖向对称轴位置逐渐向左上角移动，且区域面积逐渐减小，数值逐渐增大。通过分析不同压缩率、不同介质压力条件下，温度升高对最大Von Mises应力的影响， 得出了相同结论。 此现象是由于工作温度升高，O形圈体积膨胀， 上、下接触面压力增加， 上、下接触面所产生的摩擦力增加，接触面区域更不容易产生侧向位移，同时，温度上升使O形圈材料硬度下降，内部抵抗变形的能力降低，在受到侧向介质压力的作用下，使内部最大Von Mises应力逐渐向密封槽圆角处移动，且应力逐渐增大并集中在更小区域内。

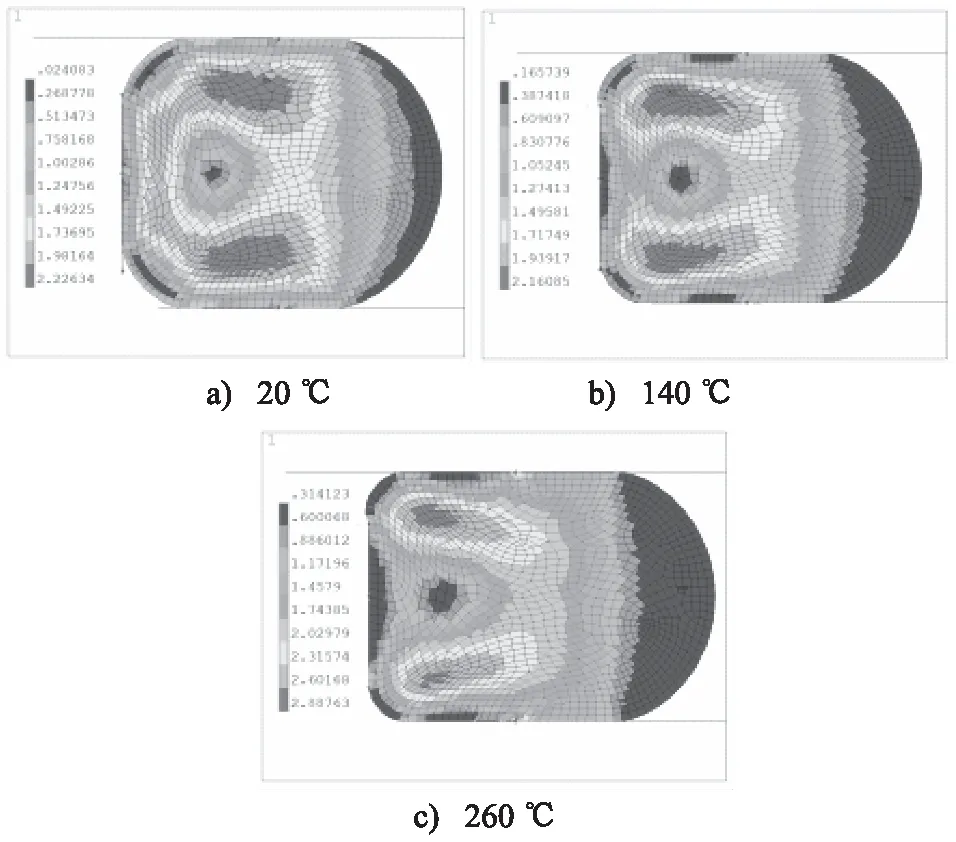
图6 不同温度条件下Von Mises应力分布规律Fig.6 Von Mises stress distribution at different temperature

3.2 不同压缩率、不同温度条件下密封特性

为了更好的说明压缩率与温度变化对O形圈密封特性的影响，分析了介质压力为2 MPa，不同压缩率、不同温度条件下O形圈最大接触应力，如图7所示。当压缩率较小时，温度对最大接触应力影响较小，而当压缩率较大时，温度对最大接触应力影响较大，这是因为当压缩率较小时，上下接触面所产生的摩擦力较小，摩擦力不足以抵抗侧向介质压力，O形圈被严重挤压在侧向密封槽壁上，此时，最大接触应力在侧向，温度升高使O形圈膨胀，膨胀所产生的侧面接触应力较小，此时温度对最大接触应力影响较小；而当压缩率增大至一定程度，最大接触应力已转移至上下接触面，温度上升使O形圈膨胀，膨胀对上下面接触应力影响较大，此时温度对最大接触应力影响较大。

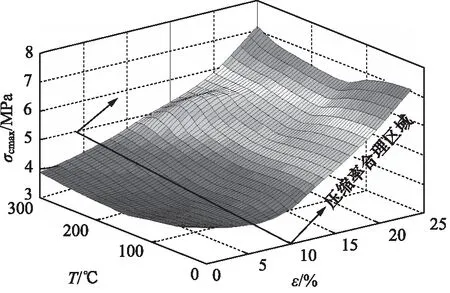
图7 不同压缩率、不同温度条件下最大接触应力Fig.7 Maximum contact stress at different compression and temperature

在温度恒定的条件下，随着压缩率增大，最大接触应力均先有所降低，而后又明显增加，因为压缩率增大使上下接触表面压力增加，上下面接触应力有所增加，同时，压力所产生抵抗侧向介质压力的摩擦力增大，从而使侧向接触应力减小，在最大接触应力由侧向逐渐向上下面转移的过程中，最大接触应力是逐渐降低的；

当压缩率达到一定时，温度升高先使最大接触应力下降，之后使最大接触应力增加，因为温度的上升使材料硬度降低，上下面的接触应力有所降低，但当硬度降低至一定程度时，材料膨胀又使最大接触应力有所增加。

图8可证明上述解释的正确性，在温度为150 ℃，介质压力为2 MPa条件下，当压缩率等于0%时，最大接触应力3.59 MPa位于O形圈侧面，而上下接触面应力仅为2.39 MPa，此时，上下表面存在一定泄漏风险；而当压缩率增加至10 %时，侧向接触应力逐渐减小至3.08 MPa，而上下接触面应力增加至3.97 MPa，已超过侧面接触压力。

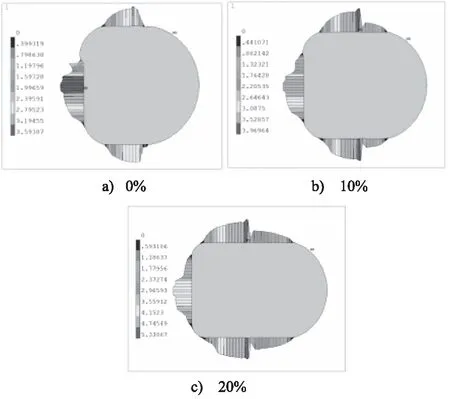
图8 不同压缩率条件下接触应力分布规律Fig.8 Contact stress distribution at different compression

图9为介质压力为2 MPa，不同压缩率、不同温度条件下O形圈最大Von Mises应力分布。如图9所示，当压缩率在0%～10%内增加时，最大Von Mises应力有所减小，在压缩率为10%处降至最低，而当压缩率继续增加时，最大Von Mises应力开始增加。因为较小的压缩率所产生抵抗侧向介质压力的摩擦力较小，O形圈被挤压至密封槽过渡圆角处，由于圆角较小，所产生的最大Von Mises应力较大，而随着压缩率增大，抵抗侧向介质压力的能力增强，最大Von Mises应力逐渐减小并向O形圈内部移动，而当压缩率超过10%且继续增加时，最大Von Mises应力有向中心扩展并形成规则矩形的趋势。图10可证明上述解释的正确性，当温度为150 ℃、介质压力为2 MPa时，随着压缩率的增大，最大Von Mises应力位置由密封槽圆角处逐渐向O形圈内部扩展，经分析，不同温度与不同介质压力条件下，压缩率增加仍有相同趋势。

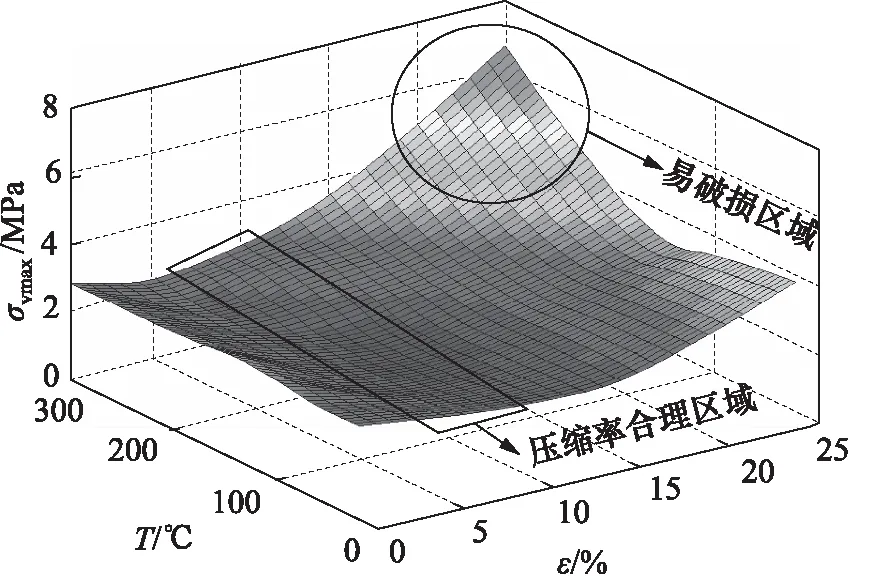
图9 不同压缩率、不同温度条件下最大Von Mises应力Fig.9 Maximum Von Mises stress at different compression and temperature

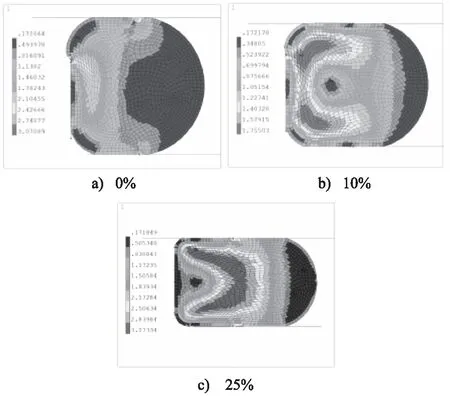
图10 不同压缩率条件下应力分布规律Fig.10 Stress distribution at different compression

综上所述，当介质压力为2 MPa时，为使O形圈有较好的密封性，主要密封面应为上下接触面，且越大的接触应力密封效果越好，此时，压缩率应大于10%，但结合压缩率对最大Von Mises应力的影响，考虑材料疲劳破坏，合理的压缩率应在10%～15%之间。同时为了防止严重疲劳破坏，应尽量避免同时满足温度高于200 ℃，压缩率高于20%的条件。

3.3 不同介质压力、不同压缩率条件下密封特性

图11、图12为温度150 ℃，不同介质压力、不同压缩率时O形圈最大接触应力、最大Von Mises应力曲面图。如图11所示，最大接触应力随介质压力与压缩率的增加呈准线性分布；如图12所示，最大Von Mises应力随介质压力和压缩率的增加均有增加，当压缩率较小时，最大Von Mises应力随着介质压力升高明显增加，因为较小的压缩率所产生的摩擦力不足以抵抗侧向介质压力， O形圈被严重挤压在密封槽圆角处，使最大Von Mises应力明显增加。

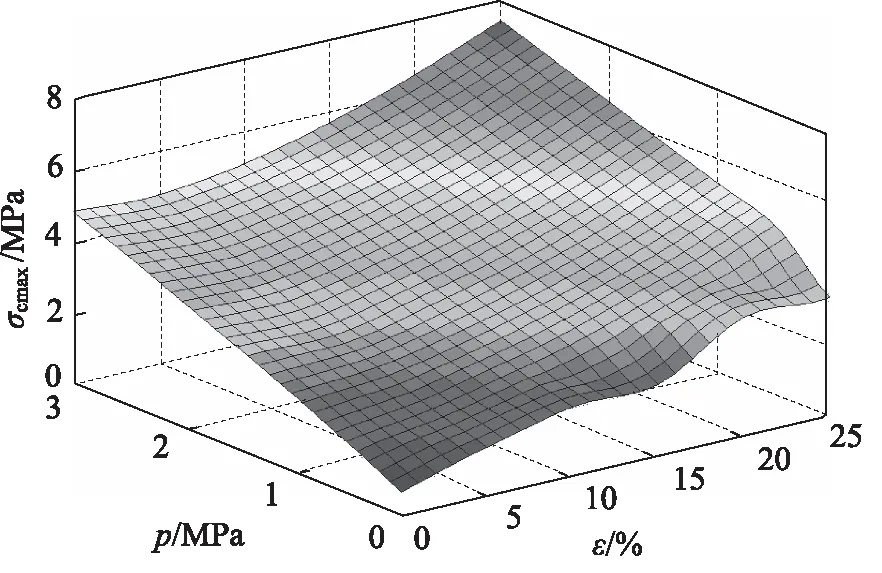
图11 不同介质压力、不同压缩率条件下最大接触应力Fig.11 Maximum contact stress at different pressure and compression

图12 不同介质压力、不同压缩率下最大Von Mises应力Fig.12 Maximum Von Mises stress at different pressure and compression

图13为温度150 ℃， 压缩率15%，介质压力为0， 1， 3 MPa时的Von Mises应力变化，随着介质压力的增大，最大Von Mises应力由O形圈内部向密封槽圆角处移动，当介质压力为3 MPa时，已到达密封槽过渡圆角处。

图13 不同介质压力条件下Vons Mises应力分布规律Fig.13 Von Mises stress distribution at different pressure

而当介质压力较高时(3 MPa)，最大Von Mises应力随着压缩率的增大明显减小。这是因为当压缩率增大时，O形圈抵抗侧向介质压力的能力增强，使最大Von Mises应力由密封槽圆角处向O形圈内部转移，且数值有所降低。这些现象都是由介质压力与压缩率平衡决定的。

4 结论

本研究采用ANSYS有限元分析软件，研究了低压铸造中O形圈实际工作顺序下的Von Mises应力和接触应力的变化规律，对不同温度、压缩率、介质压力条件下的Von Mises应力和接触应力进行了分析，并给出相应解释，结论如下：

(1) O形圈易疲劳破损位置随着工作温度的升高、压缩率的减小、介质压力的升高，均由O形圈内部逐渐向密封槽过渡圆角处移动；

(2) 当介质压力为2 MPa时，合理的压缩率应在10%～15%内；当温度高于200 ℃，且压缩率高于20%时，破损风险明显增加；

(3) 当温度为150 ℃时，介质压力高于2.5 MPa且压缩率小于5%时，破损风险明显增加；

(4) 不同温度、介质压力的条件下，较小的压缩率不仅会使密封性能降低，而且还会使破损机率增加。