基于模型预测控制的主动四轮转向车辆稳定性研究

张海川

基于模型预测控制的主动四轮转向车辆稳定性研究

张海川

（长安大学 汽车学院，陕西 西安 710064）

为提高汽车在高速、低附着系数路面下的操纵稳定性，论文设计模型预测控制器跟踪线性二自由度理想模型，得到横摆角速度与质心侧偏角偏差，然后由二次规划算法计算实际的四个车轮转角，并在Carsim软件中建立开环角阶跃工况进行联合仿真。结果表明：文章所设计的基于模型预测控制的主动四轮转向汽车相对于前轮转向，能够有效降低整车角阶跃输入下的横摆角速度与质心侧偏角，更好地跟踪理想控制目标，主动四轮转向汽车提高了整车的操纵稳定性和路径跟随精度。

四轮转向；模型预测控制；操纵稳定性；二次规划

引言

随着汽车智能化、电动化技术的发展，四轮转向和线控转向技术成为近年来的研究热点。主动四轮转向技术取代了之前方向盘与车轮之间的机械耦合，由控制器根据当前整车行驶状态决策实际前后轮转角，实现了更好的操纵稳定性和行驶安全性。主动四轮转向汽车控制器的设计方法方法有很多：赵立军等[1]研究了四轮转向/驱动车辆，采用滑膜变结构对车辆转向稳定性进行控制；杜峰等[2]研究了基于最优控制的主动四轮转向汽车闭环系统的稳定性；张庭芳等[3]采用改进型滑膜控制，研究了线控四轮转向汽车受侧向干扰下的稳定性问题；Ke Shi等[4]针对主动四轮转向多输入、多输出的耦合系统，采用解耦控制和模型预测控制的双层控制系统来提高车辆的稳定性和路径跟随性能。目前主动四轮转向汽车控制策略在进行仿真验证时多以matlab搭建的整车模型为研究对象，模型精度不能很好地模拟实车行驶状态。本论文以Matlab/Carsim软件车辆作为研究平台，运用模型预测控制算法，以横摆角速度、质心侧偏角等参数作为控制目标，对主动四轮转向汽车进行研究。

1 四轮转向汽车横向动力学模型

本论文需要建立汽车横向动力学模型封装在S-function，进行模型预测控制算法研究。考虑到汽车在小转角行驶工况下，侧向加速度小于0.4，整车模型可简化为2自由度线性模型，该模型可以很好地模拟车辆转向过程，预测未来一段时间内整车行驶状态。4WS 汽车线性2 自由度动力学微分方程为：

式中：为整车质量；为质心侧偏角；v为汽车纵向速度（匀速）；v为汽车侧向速度；为汽车横摆角速度；I为整车绕z轴的转动惯量；k、k分别为前、后轴等效侧偏刚度；、分别为质心至前、后轴距离；δ和δ分别为汽车前、后轮转角。

2 主动四轮转向汽车模型预测控制器设计

模型预测控制（MPC）具有预测、滚动优化和反馈校正的基本功能，尤其适用于线性动力学模型、不确定环境干扰下且存在约束条件的控制系统，对解决汽车横摆稳定性问题具有独特的优势。文中选用此算法对四轮转向车辆稳定性控制研究思路：首先采用前向欧拉转化把连续的线性时变系统模型离散化，然后根据离散化的系统递推预测时域内质心侧偏角和横摆角速度的输出量，最终采用二次规划算法计算前后轮转角控制增量，使得整车状态量偏差值最小。

2.1 车辆参考模型

车辆的稳定性控制目标通常可以根据理想线性二自由度车辆模型产生，建立运动微分方程如下：

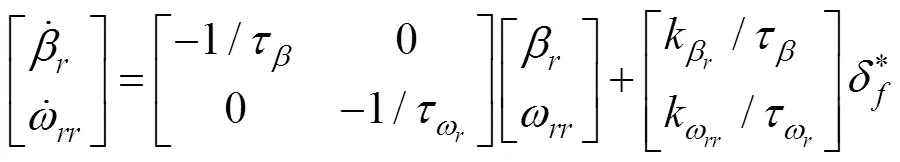
式中：δ为参考前轮转角；β为参考质心侧偏角；ω为参考横摆角速度；τ、τ为时间常数，本文取值为0.1；k、k为质心侧偏角、横摆角速度稳态增益[1]。

2.2 模型预测控制器

2.2.1 线性模型的离散化

将线性连续模型转化成了离散线性时变模型，便于MPC控制器的设计。

2.2.2 预测模型的推导

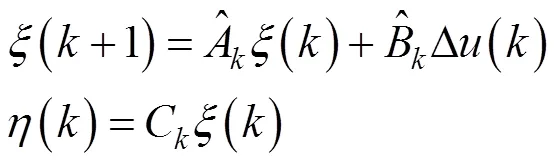
预测时域内的输出量即未来一段时间内横摆角速度、质心侧偏角的大小，通过当前时刻已知的状态量、上一个时刻已知的控制量和控制时域内未知的控制增量计算得到，具体如下：

2.2.3 二次规划问题

将线性动力学模型利用MPC转化为二次规划问题，定义目标函数：

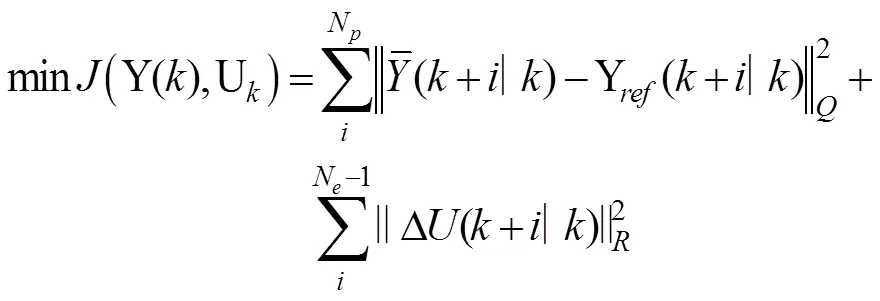
将上式目标函数转化为二次规划问题，不等式约束即为前后轮转角的范围和前后轮转角控制增量的界限值。在每个控制周期完成对式（6）的求解后，得到了控制时域内的一系列控制输入增量，将该控制序列中第一个元素作为实际的控制输入增量作用于系统，得到作用于Carsim模型中的前后轮转角。

3 控制仿真分析

基于Matlab/Carsim建立4WIS动力学仿真平台，Carsim车辆模型默认为传统前轮转向汽车，在主动四轮转向仿真平台，需要断开前轮转向系统，论文在Carsim的高级设置里面依次输入opt_steer_ext(1) 4和opt_steer_ext(2) 4，使得Carsim车辆模型具备主动四轮转向能力。

论文利用设计的Matlab/Carsim4WIS动力学仿真平台用于横摆稳定性的仿真验证，仿真平台如图1所示，车辆参考模型根据Carsim得到的车速和方向盘参考转角计算横摆角速度与质心侧偏角参考值，S-function函数根据得到的质心侧偏角、横摆角速度的理想值与实际值，利用MPC控制算法，得到最终前后车轮转角控制量，作用于整车。主要的车辆参数为：空载质量1 415.51 kg，整车绕轴转动惯量1 536.7 kg·m2，质心到前轴距离1.015 m，质心到后轴距离1.895 m，前轴等效侧偏刚度－163 859 N·rad-1，后轴等效侧偏刚度－84 450.94 N·rad-1。

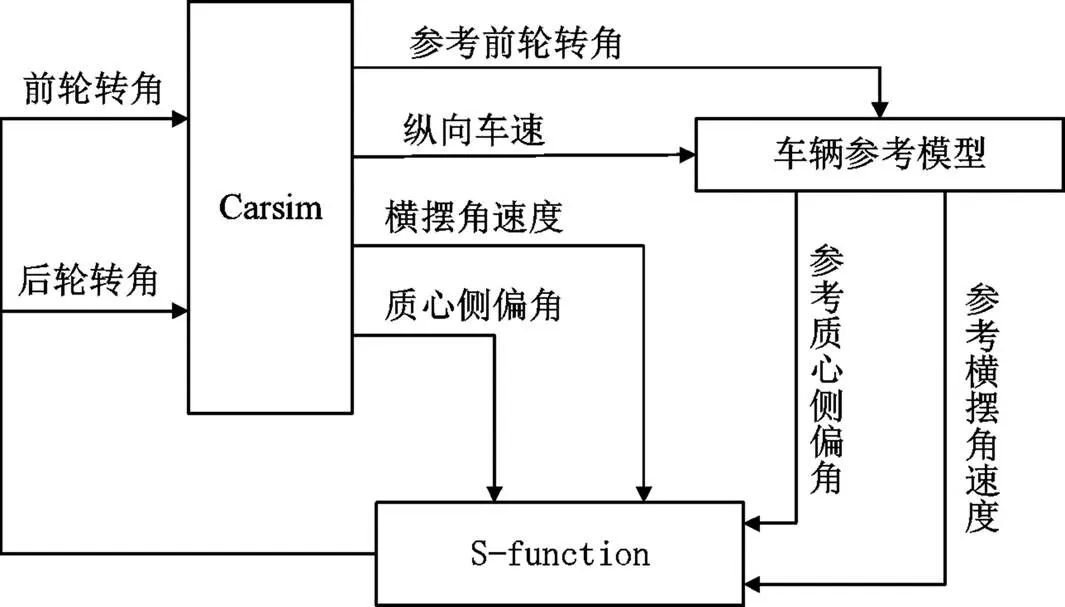
图1 Matlab/Carsim4WIS动力学仿真平台

车辆进行高速转向行驶时，为了验证MPC控制的有效性，选取一组实验数据：其中预测时域N=5，控制时域N=3，设车辆的纵向速度为72 km/h，地面附着系数为0.6，右前轮转向角初始值为0，斜率为0.024 rad /s，经过1 s 后达到0.024 rad，然后保持不变。仿真结果如图2—图4 所示，分别对比图2、图3可以看出，进行模型预测控制之后的质心侧偏角和横摆角速度都非常接近参考值，很好地达到了预期目标，提高了车辆的稳定性．进行模型预测控制之后，质心侧偏角值和横摆角速度值有很小幅波动，这是MPC控制的固有缺陷。在实际运用中可根据需求和系统特性采取减小波动的措施。图4为该工况下的各轮转角，可以看出，当车辆以较高速度行驶时，车辆的前后轮同向转动。

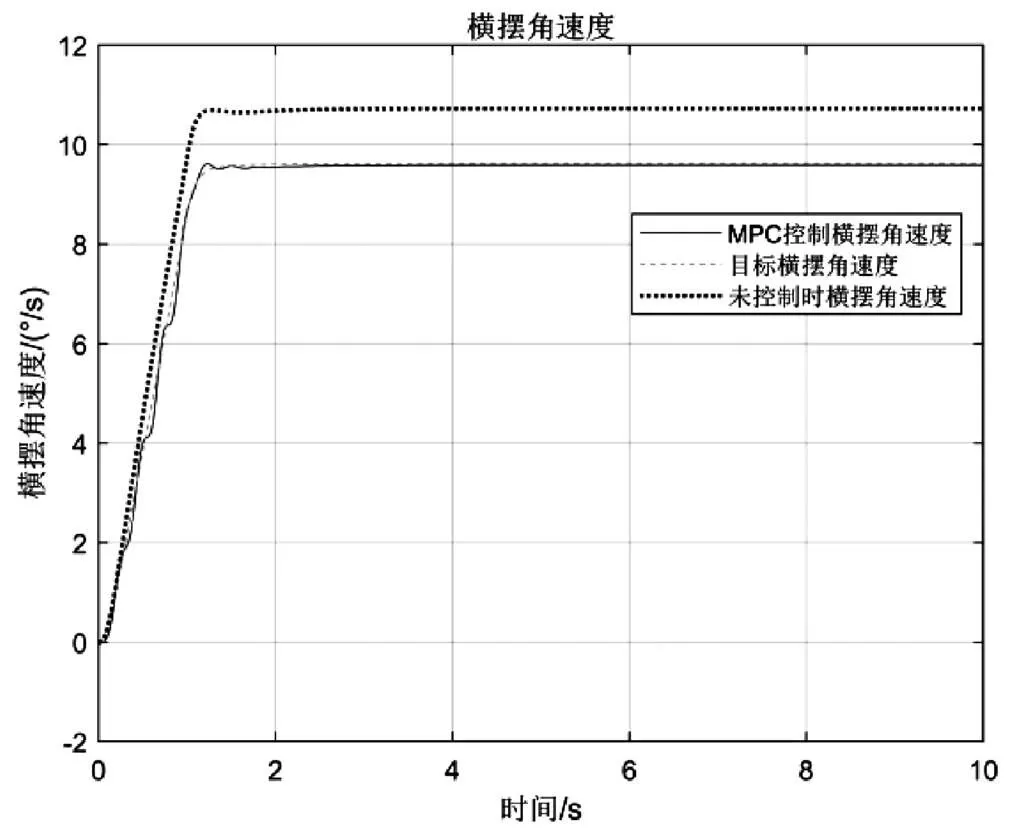
图2 横摆角速度

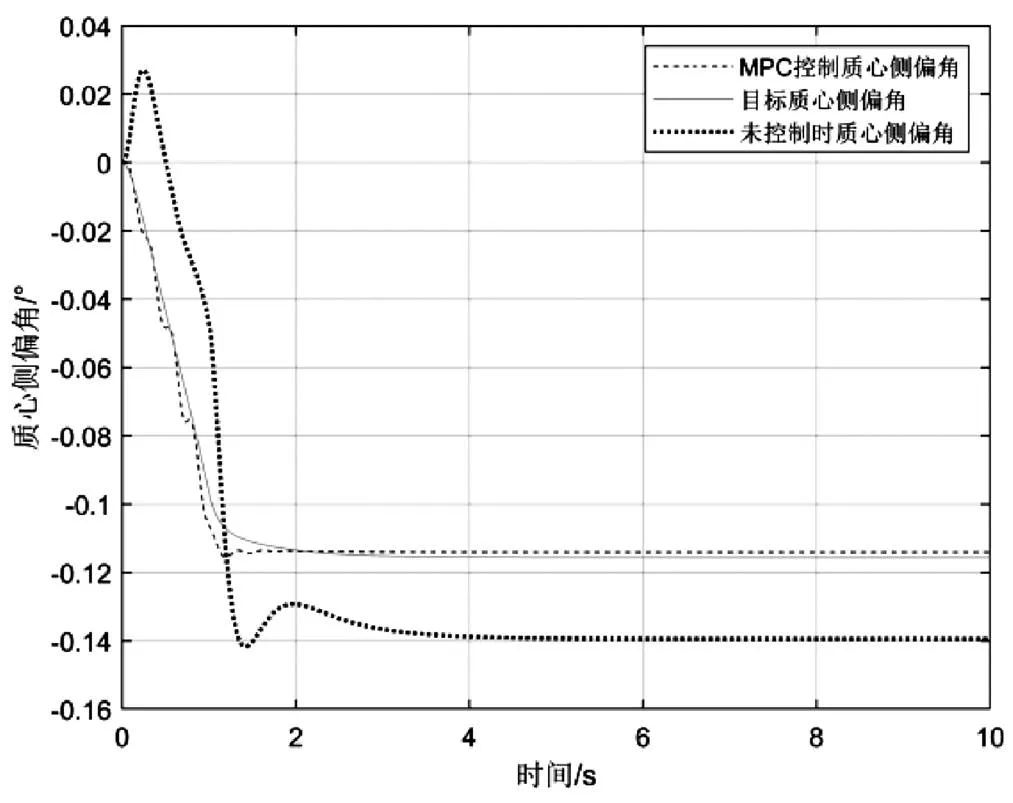
图3 质心侧偏角

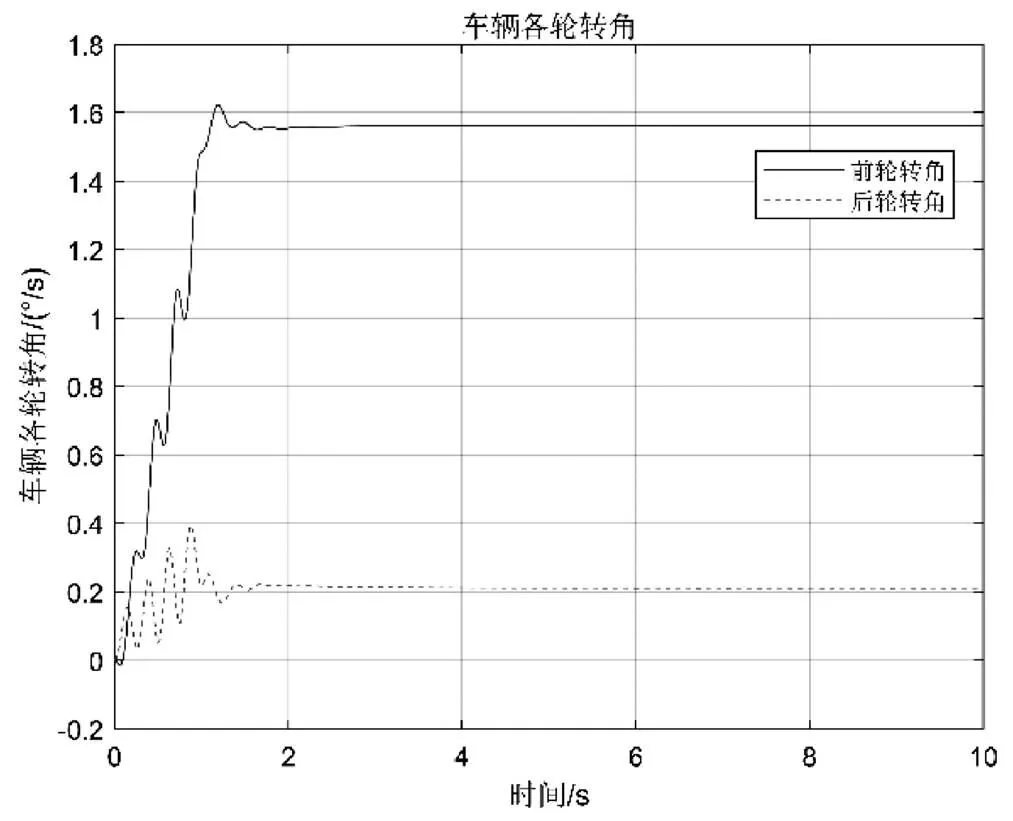
图4 车辆各轮转角

4 结语

本论文以Carsim搭建的主动四轮转向车辆为研究对象，通过模型预测控制算法预测未来一段时间内质心侧偏角和横摆角速度的偏差值，利用二次规划算法控制车辆前后轮的转角，且对该控制算法进行了开环角阶跃控制。仿真验证表明：该控制算法使得横摆角速度和质心侧偏角很好地跟踪期望值，提高了整车的稳定性和路径跟随性能。

[1] 赵立军,邓宁宁,罗念宁,等.基于直接横摆力矩的四轮转向/驱动滑模控制[J].华南理工大学学报(自然科学版),2015,43 (08):69-74+81.

[2] 杜峰,闫光辉,魏朗,等.主动四轮转向汽车最优控制及闭环操纵性仿真[J].汽车工程,2014,36(07):848-852.

[3] 张庭芳,张超敏,刘明春,等.基于改进型滑模控制的4WS汽车控制策略研究[J].北京理工大学学报,2017,37(11):1129- 1136.

[4] Shi K,Yuan X,He Q.Double-layer Dynamic Decoupling Con- trol System for the Yaw Stability of Four Wheel Steering Vehicle[J]. International Journal of Control, Automation and Systems,2019.

Research on Stability of Active Four Wheel Steering Vehicle Based on Model Predictive Control

ZHANG Haichuan

( School of Automobile, Chang’an University, Shaanxi Xi’an 710064 )

In order to improve the handling stability of the vehicle on the high-speed and low adhesion road, this paper designs a model predictive controller to track the linear two degree of freedom ideal model, obtains the yaw rate and sideslip angle deviation, and then calculates the actual four wheel angles by quadratic programming algorithm. Establishing the open-loop angle step condition in Carsim software, this paper verifies the effectiveness of the algorithm. The results show that: compared with the front wheel steering, the active four-wheel steering vehicle based on model predictive control designed in this paper can effectively reduce the yaw rate and mass center side slip angle under the vehicle angle step input, and better track the ideal control target. The active four-wheel steering vehicle improves the vehicle handling stability and path tracking accuracy.

Four wheel steering; Model prediction control; Handling stability; Quadratic programming

U461.6

A

1671-7988(2022)02-115-04

U461.6

A

1671-7988(2022)02-115-04

10.16638/j.cnki.1671-7988.2022.002.026

张海川，就读于长安大学汽车学院。