面向平行系统的飞行器航迹仿真模型架构设计
王凯旋,李 烨,薛晨琛,董 宇
(中国运载火箭技术研究院,北京 100076)
0 引言
通过构建人工系统与实际系统同步进行大规模并行仿真计算,并采用平行执行的方式进行虚实互动,是采用平行系统方法解决复杂自适应系统不可准确预测、难以拆分还原和无法重复试验等问题主流技术途径。通过实际系统与虚拟系统协同演化、闭环反馈和双向导引,实现对实际系统的目标优化是平行系统的重要特征。在平行系统中,核心问题之一是在“虚”和“软”的平行空间内构建支持平行执行的高置信度仿真模型,以在极限加速条件下随时完成状态转移和更新,并通过大规模高效并行及时得到全面、准确、可量化的复杂系统最优策略方案。因此,研究准确、高效、灵活的航迹仿真模型架构,实现飞行器航迹仿真计算对平行系统的支持,对面向飞行器的平行系统构建具有重要意义。
1 研究现状
目前,与飞行器航迹计算相关的软件研究较多,但大多集中在对航迹计算方法、航迹仿真和软件实现方案等研究,针对航迹仿真模型架构设计的研究较少。在针对航迹计算的软件实现研究中,大多以面向过程的方式实现航迹计算模型及软件的设计,尚无面向平行系统运行所需的并行化使用模式及按照面向对象的方法基于状态转移模型对架构进行分析和设计的案例。在面向平行执行的仿真模型建模方面,通常较少考虑飞行器特性或飞行航迹本身的特点,使用常规的路径搜索或航迹点规划算法生成飞行约束完成计算,对面向平行系统并行航迹计算方面的研究较少。
2 离散化航迹计算架构设计
由于飞行器航迹计算是关于时间的连续过程,且按照时间的方向顺序转移,当不考虑后续状态对当前状态的影响时,飞行器的飞行过程满足无后效性,可以使用马尔科夫决策问题(MDP)模型来描述离散化航迹计算问题,飞行器以时间间隔Δ动态改变其状态,状态转移方程由飞行器运动学模型得到。为了控制飞行器的运动状态,与不同状态之间的变化相关的控制变量为,与飞行器本身相关的运动学参数为。根据飞行器运动学模型构建航迹计算模型的状态转移模型
=(-1,,)
因此,飞行器的飞行过程可以看作给定完备的环境模型的MDP问题,可使用状态转移的方法进行并行航迹计算。
航迹仿真模型按照飞行器运动学方法,使用积分迭代完成飞行器全程的航迹计算,模拟飞行器的连续飞行过程。为了使航迹计算过程能够适应离散化状态,需要对软件进行针对性的架构设计,满足不同状态之间的状态转移;在平行系统执行过程中,由于存在不确定性和随机性的影响,航迹计算模型要适应从任意状态开始的并行计算需求。
3 仿真模型架构设计
按照面向对象的软件设计方法,对飞行器航迹计算模型进行分析,将计算过程与计算数据分离,提取支持模型计算的类及各类之间的关系,构建基础积分模型类、航迹积分模型类、航迹计算模型类和实体模型类,每个类负责各自的核心计算数据和核心计算功能,其架构如图1所示。此架构为航迹数据管理、航迹计算管理、飞行状态转移机制设计、广度优先并行化计算的设计与实现奠定了基础。

图1 模型架构Fig.1 Model infrastructure
3.1 基础积分模型
基础积分模型是进行积分迭代的基础,其内部实现了具体的积分算法和积分机制,具体功能为:
1)初始化功能,初始化用于积分的变量,采用数组方式管理积分变量;
2)更新积分数据功能,更新用于积分迭代的积分变量和被积分量;
3)积分迭代功能,按照指定的步长和指定的计算模型完成对积分量的计算。
3.2 航迹积分模型
航迹积分模型包含基础积分模型,是实现航迹积分及其控制的基础。具体功能为:
1)积分计算模型定义功能,在积分计算模型中定义虚函数,预留航迹计算模型接口;
2)航迹积分起停判定功能,提供对是否停止积分进行判定的接口虚函数,作为航迹积分控制的起停条件;
3)积分计算控制功能,根据航迹计算中积分的起停条件,完成计算模型调用和积分模型更新。
3.3 航迹计算模型
航迹计算模型继承于航迹积分模型,定义了航迹计算所需的基础数据,实现与航迹计算相关的功能和流程控制,具体功能为:
1)飞行阶段判定功能,根据当前状态对飞行阶段进行判断,并按照飞行阶段进行相关解算;
2)运动学计算功能,按照飞行器动力学方程,完成相关基础计算;
3)数据采样控制功能,按照一定采样周期,完成对各类基础数据的采样;
4)辅助量计算功能,按照标准化航迹计算模型,完成对气动、地理数据、坐标转换矩阵等计算。
3.4 实体模型
实体模型继承于航迹计算模型,并对航迹积分模型和航迹计算模型中的虚函数进行实现。实体模型中包含了与气动、动力、过载等相关的计算模型,是航迹计算模型的具体实现。实体模型可按照不同的功能、不同飞行阶段构建各类实体模型,由于所有实体模型中的内部数据和方法均继承于航迹计算模型,因此能够通过对实现对航迹计算模型的管理,实现不同实体模型类的统一控制和调度。
4 数据管理架构设计
根据航迹计算模型,按照在每个计算算法模块中数据结构低耦合、高重用程度优先、每次迭代计算内不变的数据只计算一次的原则,对用于计算的飞行阶段数据、初始坐标系数据、飞行任务数据、飞行器固有数据、飞行状态数据进行梳理,确定其内容和初始化顺序,如图所2示。

图2 数据模型体系Fig.2 Data model
各类数据按照基础数据和派生数据的方式进行组织。基础数据应用于航迹计算模型,属于航迹计算的共性数据,派生数据应用于实体模型,继承于基础数据。
4.1 基础数据
4.1.1 飞行阶段基础数据
飞行阶段基础数据用于控制各飞行阶段不同的计算模型,飞行阶段数据采用枚举变量确定准备、启动、起飞、飞行阶段转换等阶段。
4.1.2 任务基础数据
任务基础数据用于明确的当前状态和确定飞行任务目标,并给出由任务可确定的可复用数据,包括起飞位置、落点位置,并计算得到飞行方向和理论航程。
4.1.3 航迹固有基础数据
飞行器固有数据为常量数据,包括飞行器各组成部分的质量、长度、面积等基础数据。
4.1.4 初始坐标系基础数据
根据起起飞位置、落点位置和地球模型计算地面直角系下固有的可复用的数据,地面直角系数据包括起飞点地心矢径在初始坐标系下的分量、降落点地心矢径在初始坐标系下的分量、地球旋转角速度、起飞点的引力加速度各类与飞行位置无关的转换矩阵,如哥式加速度矩阵等。
4.1.5 飞行状态基础数据
飞行状态基础数据用于记录每个时间点的飞行状态,包括飞行时间,基本积分量(包括质量、位置、速度、加速度),空间位置量(飞行高度、纬度、经度),姿态数据量(俯仰角、偏航角、滚转角)及其他辅助量(当前航程、气压)。
4.2 派生数据
4.2.1 派生数据定义
根据不同的实体模型,可继承相关基础数据进行扩充,例如可在飞行任务数据中增加导航点约束量,在飞行状态数据中增加过载量等,具体扩充对应关系如图3所示。
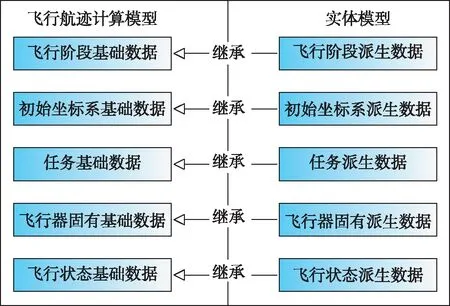
图3 数据扩充体系Fig.3 Data extension system
4.2.2 派生数据注册
在航迹计算模型中,声明指向基础数据的指针并完成基础数据的动态初始化和注册;在实体模型中,各派生数据可按照基础数据父类类型进行重新注册和替换,由航迹计算模型负责派生数据中基础数据部分的赋值和操作,由实体模型完成派生数据中新增部分的赋值和操作,从而在不改变航迹计算模型结构的情况下实现了自定义数据扩充。
5 计算流程架构设计
按照航迹积分模型、航迹计算模型和实体模型分治协作的方式,完成航迹计算。其中航迹积分模型负责航迹基础积分模型初始化和积分起停控制;航迹计算模型负责飞行阶段判别和各飞行阶段解算控制;在实体模型中对虚函数进行实现,定义具体的计算模型并完成辅助计算量的解算。计算过程如图4所示,其中“(v)”表示虚函数,“call”表示方法调用。
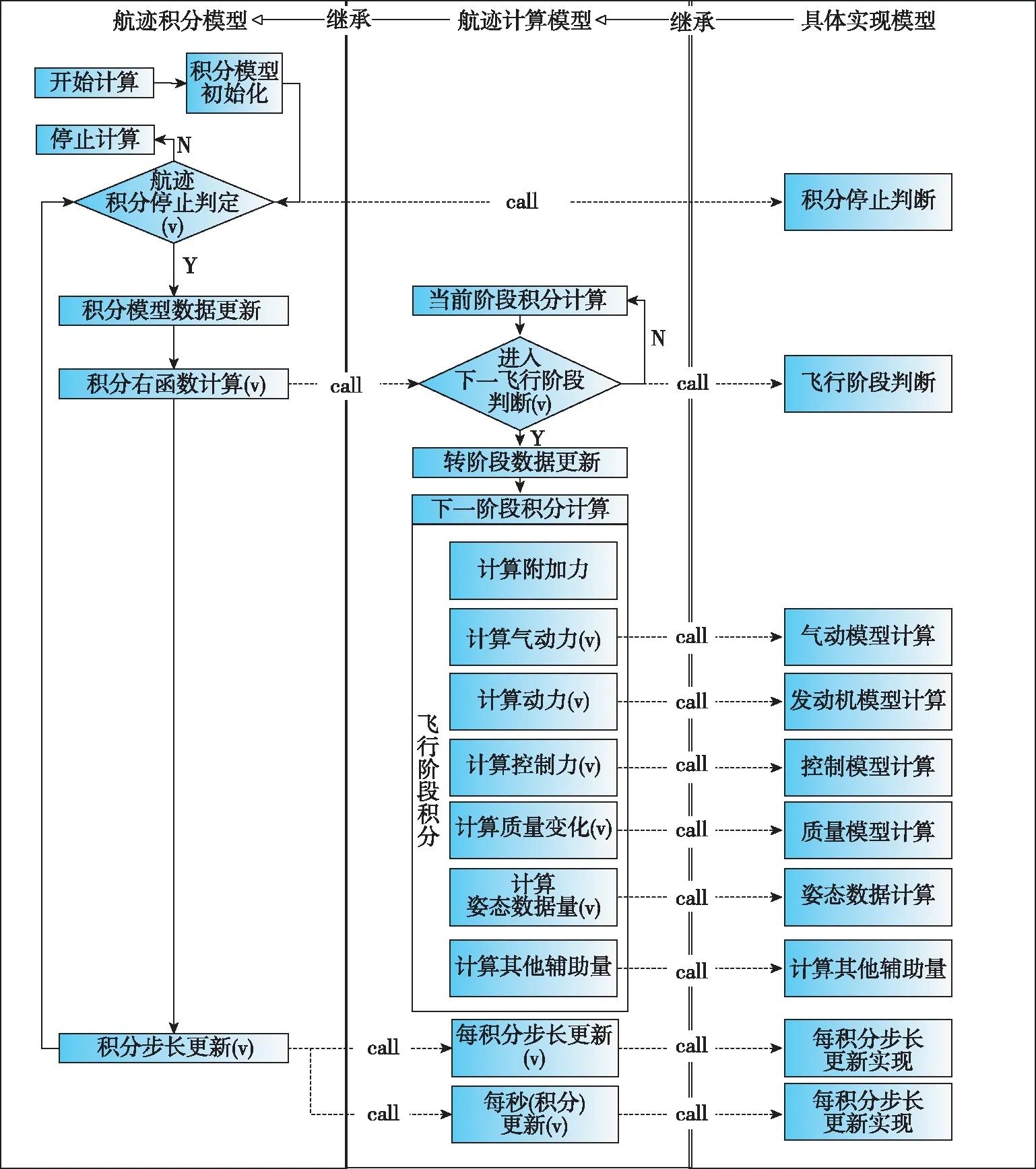
图4 航迹计算流程Fig.4 Track calculation process
6 飞行状态转移设计
由于实体模型均继承于航迹计算模型,与航迹计算的基础数据完全兼容,因此在保证派生数据兼容的情况下,可以实现不同实体模型对象和同一实体模型对象由上一状态到下一个状态的完全平滑的状态转移。使用状态转移数据包来实现不同状态之间的转移,状态转移数据包以飞行阶段数据、初始坐标系数据、飞行任务数据、航迹固有数据、飞行状态数据为基础,加入航迹积分模型中的积分变量,可一次性完成对基础积分模型、航迹积分模型、航迹计算模型和实体模型的数据更新,从而保证转移前后的两个实体模型处于同一状态,实现不同飞行状态不同实体计算模型的飞行状态转移。飞行状态转移机制如图5所示。
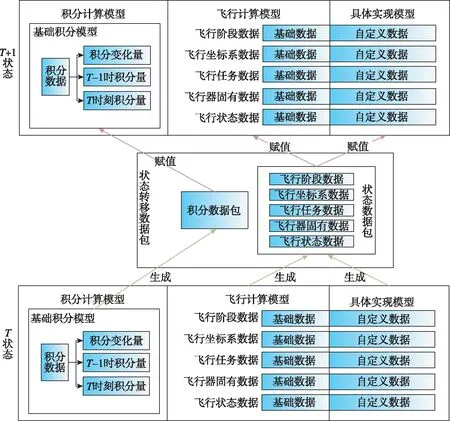
图5 飞行状态转移机制Fig.5 Flight status transfer mechanism
7 飞行航迹平行执行设计
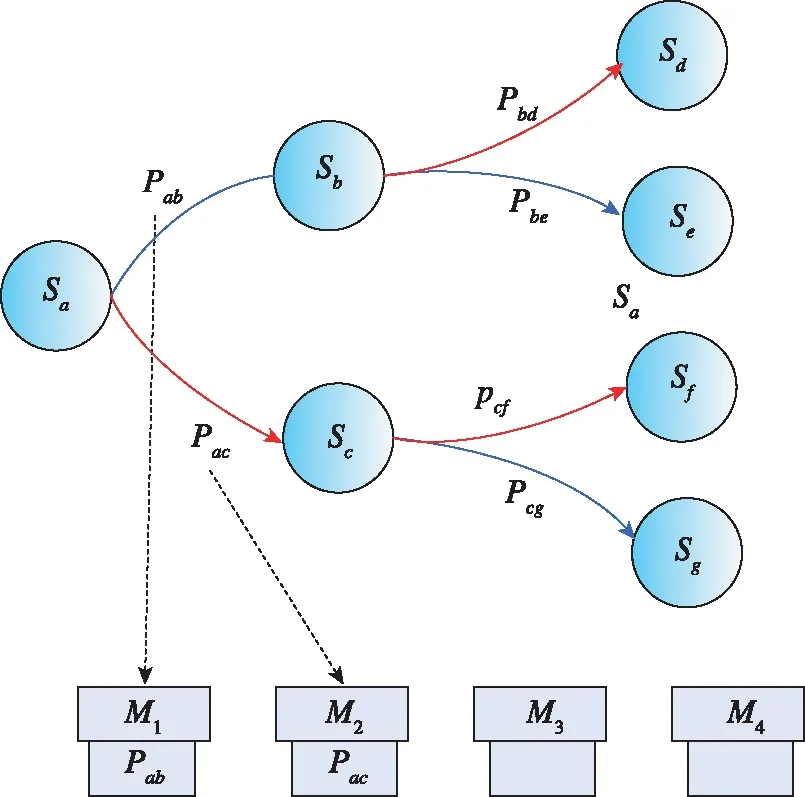
传统的航迹计算方式为按照深度优先的方式,可使用逐条计算的并行方法对所有航迹进行遍历。因此使用传统的并行模式进行平行执行会产生大量的重复计算,且无法进行阶段迭代。传统的航迹计算状态转移方式如图6所示。

图6 状态转移图Fig.6 State transition diagram
由于实体模型以按照面向对象的方法进行设计,在任意状态均可记录当前状态及决策参数,也可以任意状态为起点进行计算,此架构能够解决多阶段迭代问题,避免大量的重复计算。针对并行化需求,本软件架构可支持使用线程池或分布式技术构建多个实体模型对象容器,并由调度模型控制其进行相关并行计算,容器中可接收用于计算过程的实体模型对象,如图7所示,模型对象的切换通过状态转移数据包及状态转移机制进行。
(a) 一阶段计算
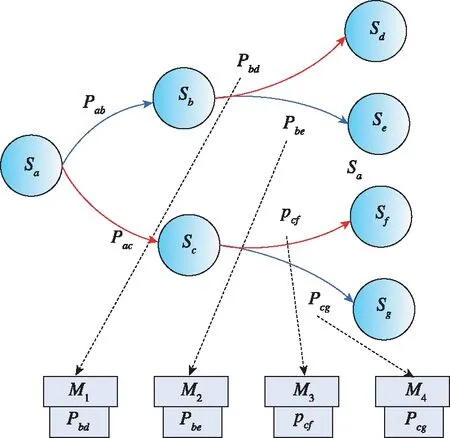
(b) 二阶段计算图7 并行计算过程Fig.7 Parallel computing process
由于采用了面向对象的软件设计方法,并充分考虑多飞行阶段状态转移的情况,推进式状态转移模型和反馈式状态转移模型可实现针对不同飞行阶段的并行计算,在大规模平行执行中有显著优势。
8 结论
本文面向平行系统,构建了基于状态转移模型的面向对象的航迹仿真模型架构,实现了数据与计算方法的分离,并通过状态转移机制实现了航迹计算的并行化和面向平行执行的广度优先航迹计算,为航迹计算模型的架构设计提供有力的支撑;在此基础上,完成了对航迹计算相关的状态转移类型的分析,为面向随机起点的大规模并行航迹计算奠定了理论基础。

