基于K-means++时间聚类的飞行航迹预测
郭宪超,李廷元
(中国民用航空飞行学院计算机学院,广汉 618307)
0 引言
近年来,随着我国民航业的快速发展,我国航空公司的机队规模也在迅速壮大,航空器数量的飞速增长使飞行流量冲突问题变得越发严重,所以,如何在现有民航系统条件下提高飞行流量预测的准确性成为当今民航业研究的热点。
目前对空中交通流量进行预测的主要思路是通过预测航空器的飞行航迹进而实现某一空域内空中交通流量的预测。交互式多模型跟踪滤波(IMM)航迹预测算法可以有效改善以往航迹预测算法的精度,适用于短期区域内的飞行流量预测;也有学者通过使用深度学习神经网络算法进行航迹预测,预测模型融合了卷积神经网络算法和长短期记忆网络算法,通过分析仿真实验结果表明该组合模型相比单一算法的模型具有更高的预测精度;同样,通过分析战术预测的特点进行航迹配对也是航迹预测的一种方式,该算法综合各种算法的特点进行4D计划飞行航迹的构建,可以将动态飞行数据与计划飞行航迹相融合,最终实现航空器4D航迹的实时更新。目前的航迹预测算法对时间数据和航空器的飞行航迹特征的预测并不理想,而通过聚类算法对飞行航迹数据进行聚类可以有效改善上述问题。
针对目前航空器飞行航迹预测算法的不足,本文提出一种基于K-means++时间聚类的飞行航迹预测方法,通过K-means++算法对时间数据进行聚类,使用修正欧式距离算法进行航迹相似度计算的改进型聚类算法,使用实际飞行航迹历史数据进行案例实验,实验结果表明,该算法具有较高的预测精度。
1 K-means++时间聚类算法
1.1 算法主体思想
由于机场区域的相关飞行限制,使得该区域内航空器的飞行航迹具有规律性,同时ADS-B数据主要由航空器的经度、纬度、高度和飞行时间等信息构成,所以ADS-B航迹数据中包含了大量的时间和空间信息,符合本文对航迹进行聚类的基本要求。ADS-B数据中的每条航迹都会有单独的一个航班号与之对应,所以每条航迹的组成格式为:

在上式中,代表某条单独的航迹,代表其中的航迹点,该条航迹由个航迹点组成,同时每个航迹点中都三维位置信息和发布时间信息4个属性的信息,即x,y,z,t。
如若按照时间顺序排列,机场扇区内的ADS-B数据严格意义上来说就是扇区内所有航迹组成的航迹数据集,即:

对时间进行归一化处理,使每条聚类航迹都有统一的起始时间,然后使用K-means++算法进行时间聚类,同时在进行时间相似度计算时使用修正欧氏距离算法,可以大大提高航迹预测过程中时间预测的准确性;再对飞行航迹阶段进行划分,在直线阶段使用模糊聚类法进行航迹聚类,在转弯阶段使用DBSCAN时间序列聚类法进行航迹聚类,这样可以提高航迹聚类结果的准确性;最后通过修正聚类航迹得到预测航迹。
1.2 时间归一化及时间K-means++聚类
本文选取的ADS-B数据为绵阳机场扇区内4月份的数据,进行时间聚类时首先要对时间数据进行归一化处理,将所有航迹的起始时间定义为第1秒,这样可以得到每条航迹的飞行时间T,然后使用K-means++算法对其进行聚类处理,可以得到更为准确的航行时间T,所有航迹的时刻点t按照下述公式来进行在[0,T]运行区间内的归一化:

时间归一化处理完成后,接下来需要对时间数据进行K-means++聚类,在时间聚类阶段使用修正欧氏距离作为相似度的划分标准。
首先需要确定最终的簇类数量,从个数据中随机挑选1个数据作为聚类中心点,然后计算剩余的-1分数据点之间的修正欧式距离:

上式中,x和x分别代表数据集中包含的-1个剩余数据的任意两个数据点。
接下来我们需要在-1个数据点中选取剩下的-1个聚类中心,计算剩余数据点与的距离,距离越远的数据点被选为下一个聚类中心的概率就越大,而概率计算方法为轮盘法,然后不断重复该步骤,直到个聚类中心点,…M被选择出来为止。按照修正欧氏距离算法来将剩余的-个数据点划分给与之相距最近的聚类中心形成新的类,使用均值法计算每个新类的中心点,最后执行K-means聚类算法的迭代过程,直至所有数据被分配完毕。
1.3 飞行航迹阶段聚类
1.3.1 直线阶段聚类
虽然航迹数据一般会出现数据缺失的情况,但由于飞机在直线飞行阶段的飞行状态不会出现大范围波动,所以即使出现少量航迹点数据的缺失也不会使航迹聚类的结果出现较大误差。
针对上述航空器直线飞行的特征,可以将直线阶段聚类过程分为三步:
(1)通过使用采样法在航迹数据中提取出可以代表整条航迹的特征数据点M,参照文献[4]可以得知使用10%的特征点就可以代表整条直线阶段的航迹。
(2)当完成特征点M的提取后,可以得到由特征点组成的特征航迹H,接下来对特征航迹H使用模糊C均值聚类算法进行处理。
(3)时间数据经过了前文的归一化过程之后,使得所有航迹的时间区间具有相似特征,因此可以将时间维度包含到空间数据点中,所以在进行模糊C均值聚类时使用修正欧氏距离来进行对应点M(x,y,z,t)和M(x,y,z,t)之间的修正欧式距离。
1.3.2 转弯阶段聚类
飞机转弯阶段航迹的集中程度较低,所以针对转弯阶段的航迹特征,该阶段使用全时间序列聚类方法,具体步骤如下:
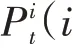

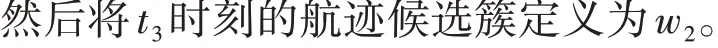
(4)当进行完所有时刻的簇类集合遍历后可以得到他们的交集,该交集在相同时间层面上存在相同对象,所以可以称之为目标簇集合;若出现遍历结束后的空集,则自动转为模糊聚类法作为直线阶段进行聚类;运算结束时可以得到聚类航迹簇的均值航迹。
1.4 航迹预测
前文曾提到,由于机场区域内各种特殊规定的限制,使得在机场区域内航空器的飞行航迹具有规律性,所以我们获得的聚类航迹具有典型性,可以通过该聚类航迹来对未来短期机场区域内航班的飞行航迹进行预测,对未来+时刻的飞行航迹进行预测的步骤为:

注:在上式中,为未来的时间量,H 代表聚类航迹,H 代表真实航迹,H 为预测航迹,∅()用来表示在时刻时真实航迹与聚类航迹对应点的误差值
2 算例实验
2.1 时间K-means++聚类仿真实验
对航迹点的时间数据进行k-means++聚类,我们将所有时间数据分为三个类:时间偏大类、中间类、时间偏小类,即为3,时间K-means++聚类结果图如图1所示。在选取完成聚类后的时间数据时只选取中间类T作为最终的聚类统一时间,得到聚类时间T=1648s,最后通过公式(4)对时间进行归一化处理。
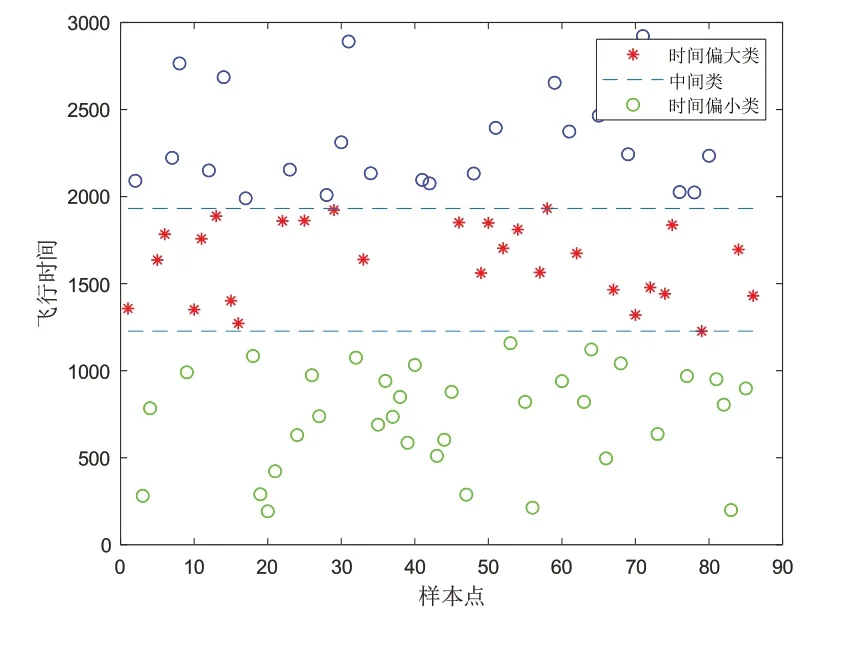
图1 时间K-means++聚类结果
2.1.1 直线阶段聚类
首先通过采样法对所有直线飞行的航迹数据进行特征点的提取,采样结果使原始的30394个航迹数据点降低为2571个,然后将提取出来的2571个航迹特征数据点使用模糊C均值聚类法进行聚类处理,如图2所示为直线第三阶段的聚类结果,其中的红色“.”代表历史真实航迹点,而绿色“*”代表直线阶段聚类航迹点。
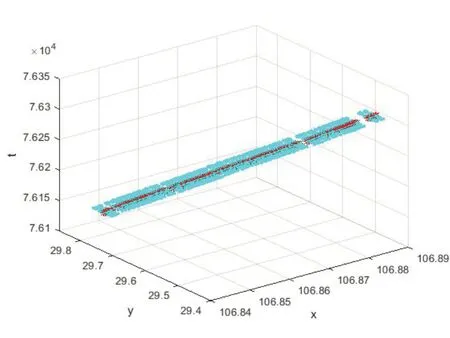
图2 直线阶段聚类
2.1.2 转弯阶段聚类
对每条转弯航迹数据点进行3次插值处理,对补全的航迹数据进行时间间隔为4 s的重新取样,然后进行DBSCAN聚类;在对每个时刻的聚类结果完成遍历搜索后,得出的转弯阶段航迹聚类结果如图3所示,其中红色点集为历史航迹点,绿色点集为聚类航迹点。

图3 转弯阶段聚类
2.2 航迹预测
如图4所示为CSC8564航班的预测航迹与真实航迹对比图,图中红色航迹为预测航迹,绿色航迹为实际航迹,图5所示为预测航迹与真实航迹平方误差图,从图中可以看出误差方差值在0~0.3之间,由此可知,该算法具有较高的预测精度。
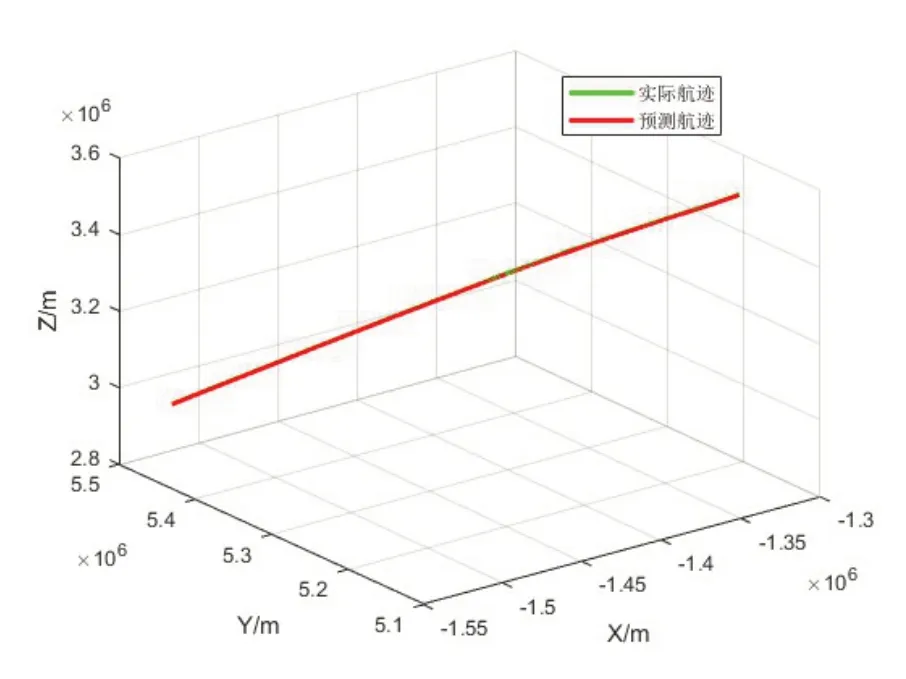
图4 预测航迹与真实航迹对比
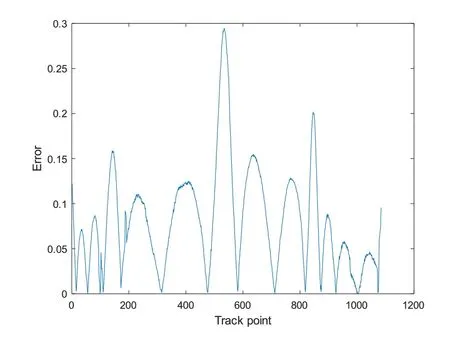
图5 预测结果误差
3 结语
本文针对传统航迹聚类预测算法对时间数据预测不准确的问题提出了一种基于K-means++时间聚类的航迹预测算法。该算法使用ADS-B数据作为数据源,通过K-means++算法对时间数据进行聚类,使用修正欧式距离算法进行航迹相似度的计算,根据直线阶段和转弯阶段的特征分配不同的聚类方法得出聚类航迹。最后对聚类航迹进行当前位置修正得到预测航迹。通过实际航迹数据进行算例试验,结果显示该预测算法具有较高的准确性。

