基于面板分位数回归的空气质量影响因素分析

姚美

摘 要：基于2018—2020年湖北省11个城市空气质量监测数据以及气象数据，采用固定效应和面板分位数回归方法，探讨了AQI的变化特征及其与污染物浓度和气象因素之间的关系。结果表明：污染物中[ PM2.5]、[PM10]、[NO2]和[O3]与AQI均呈正相关，且分位数较高时，影响作用较大;[SO2]与AQI呈负相关，且在任何分位点下影响均显著;[CO]对AQI具有双重影响，低分位点呈负相关，而高分位点呈正相关。气象因素中，平均气压、相对湿度、最大风速和风向与AQI呈负相关，其中风向在0.1～0.5分位点下影响较为显著，大型蒸发量在各分位点下与AQI均呈显著正相关，日照时长仅在0.1和0.25分位点下对AQI显著的正向影响。

关键词：AQI;气象因素;分位数回归;面板数据

中图分类号 X51 文献标识码 A 文章编号 1007-7731（2022）02-0147-06

Abstract： Based on the air quality monitoring data and meteorological data of eleven cities in Hubei Province from 2018 to 2020， fixed effects and panel quantile regression methods were used to explore the changing characteristics of AQI and its relationship with pollutant concentrations and meteorological factors. The results show that： [PM2.5]， [PM10]， [NO2] and [O3] of pollutants were positively correlated with AQI， and the effect is greater when the quantile is higher， [SO2] is negatively correlated with AQI and has a significant impact at any quantile， CO has a dual effect on AQI， with low quantile points being negatively correlated and high quantile points being positively correlated; Among meteorological factors， average air pressure， relative humidity， maximum wind speed， and wind direction are negatively correlated with AQI. Wind direction has a significant influence at the 0.1 to 0.5 quantile， and large-scale evaporation is significantly positively correlated with AQI at each quantile. The duration of sunshine only had a significant positive effect on the AQI at the 0.1 and 0.25 quantile.

Key words： AQI; Meteorological factor; Quantile regression; Panel data

近年来，空气污染已成为城市可持续发展中日益重要的问题。据世界卫生组织报道，全球每年约有700万人死于空气污染，90%的人类呼吸的空气超过了世卫组织规定的含高浓度污染物的空气限值[1]。目前，我国的主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分发展之间的矛盾，空气污染严重影响了人们的生活质量。

一直以来，空气质量都是学术界的研究热点，学者们从多方面对空气质量展开研究，包括对影响空气质量因素的探讨和各污染物浓度的预测等，为保护环境、科学防治大气污染提供了有力支撑。空气质量不僅与大气污染物有关，而且与气象因素有着密切联系。从现有文献来看，众多学者采用相关性分析[2]、灰色关联分析[3]、多元线性回归[4]以及分位数回归方法[5]，对不同城市的空气质量指数（AQI）和污染物浓度（主要是[PM2.5]）与其他空气污染物浓度之间进行了大量的研究。

湖北省位于我国中部地区，因“九省通衢”而著称，处于国家战略中部崛起的重要支撑点，是联结长江经济带以及长江中游城市群建设的重要区域，在生态文明和健康中国建设中占有举足轻重的地位。目前，针对湖北省整体大气污染的时空分布规律、影响因素分析较少，然而城市空气质量是影响其发展的重要因素之一。为此，本研究基于湖北省11个城市的空气质量数据，以AQI为被解释变量，各污染物和气象因素为解释变量，探索湖北省空气质量时空分布特征，以期为今后湖北省空气质量的研究提供参考。

1 数据来源与统计分析

1.1 样本选取与数据来源 目前，我国各个城市基本都已具备空气监测站，可以获取空气污染物浓度的实时数据及其历史数据，进而计算出空气质量指数（AQI）。AQI是无量纲的指标，定量地描述了空气质量状况，其值越大，意味着空气污染状况越严重。自2013年以来，中国开始采用[AQI]评估空气质量，并且对城市空气质量进行分类，AQI数值大小分为6个等级：0～50为优;51～100为良;101～150为轻度污染;151～200为中度污染;201～300为重度污染;大于300为严重污染[6]。

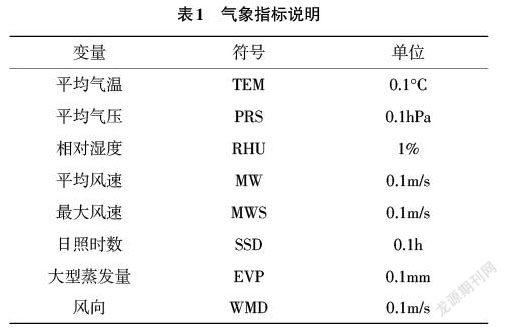
基于数据的合理性和可得性，本文选取湖北省10个地级市（黄冈、荆门、荆州、十堰、随州、武汉、咸宁、襄阳、孝感、宜昌）和1个自治州（恩施）的面板数据进行实证检验，其中包括空气质量指数、空气污染物浓度以及气象因素，空气质量数据来源于中国环境监测总站，具体指标有AQI、[PM2.5]浓度、[PM10]浓度、[NO2]浓度、[SO2]浓度、[CO]浓度及8h滑动平均[O3]浓度，气象数据来源于中国气象数据网，其中风向代表的是最大风速时风的朝向，按照16方位图进行编码，各变量的具体描述见表1。本文选取的研究时段为：2018年1月1日至2020年12月31日，由于數据在采集过程中，会因为网络信号、设备故障等原因，存在部分监测站点数据缺失的情况，经统计发现缺失数据较少，未出现大面积连续缺失的情况，因此针对缺失值采取缺失值前后2个时段数据的均值进行填补。

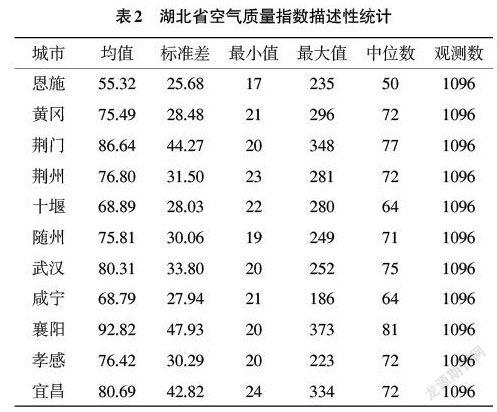
1.2 统计分析 在本研究时段内，各市AQI的基本情况描述如表2所示。由表2可知，恩施市AQI的平均值、中位数、最小值均最小，空气质量状况较全省其他城市最优，其中位数为50，说明3年内一半天气均为优状态，同时该市空气质量的波动也是最小的，较为稳定。由标准差可知，波动较小的是咸宁和十堰，波动较大的是襄阳，并且其均值、中位数和最大值都是最高的，空气污染程度较其他城市最为严重。除襄阳之外，荆门、宜昌的均值和中位数也是较高的，其AQI的最大值均超过300，这3个城市的空气污染程度较为严重。

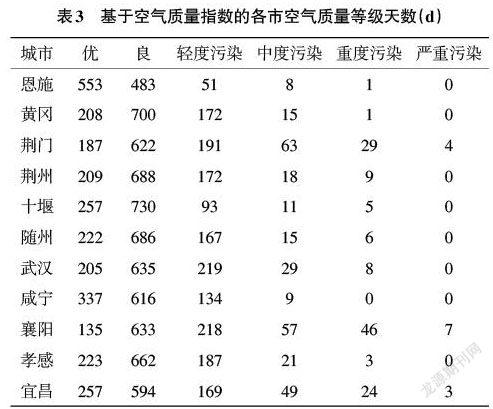
根据AQI划分等级标准，将研究时段2018年1月1日至2020年12月31日内湖北省11个城市的空气质量指数进行划分，详见表3。再从时间趋势对11个城市的空气质量变化情况进行探索，具体分析空气质量的情况，如表4所示。由表3可知，湖北省11个城市的空气质量主要集中在优、良、中度污染等级，空气质量相对全国平均水平而言，总体在中等水平，然而个别城市出现了严重污染。空气质量等级处于优天数最多是恩施，共553d，远远超过其余10个城市，接着依次分别是咸宁、十堰、宜昌、孝感、随州、荆州、黄冈、武汉、荆门、襄阳，优良天数的排序从另一方面说明了城市的空气质量状况，这与表2中所传递的信息是一致的。从逆序来看，襄阳市的优良总天数也是最少的，其中严重污染天数竟有7d，其次是荆门、宜昌和武汉，这几座城市是湖北省人口密集地区，经济规模也是位居前列，污染排放集中，可见对城市空气质量具有重要影响。

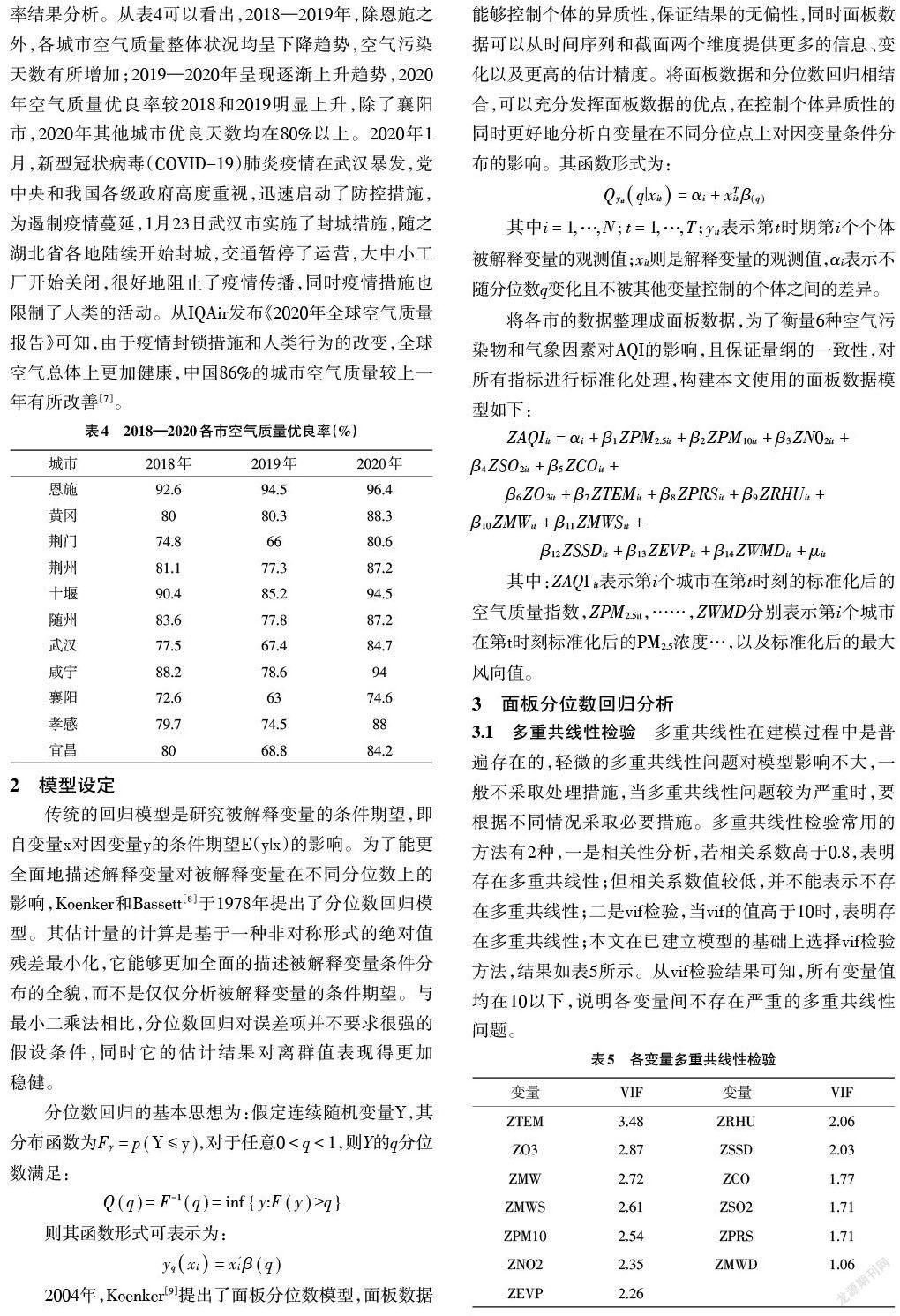
表4是对11个城市根据时间趋势进行空气质量优良率结果分析。从表4可以看出，2018—2019年，除恩施之外，各城市空气质量整体状况均呈下降趋势，空气污染天数有所增加;2019—2020年呈现逐渐上升趋势，2020年空气质量优良率较2018和2019明显上升，除了襄阳市，2020年其他城市优良天数均在80%以上。2020年1月，新型冠状病毒（COVID-19）肺炎疫情在武汉暴发，党中央和我国各级政府高度重视，迅速启动了防控措施，为遏制疫情蔓延，1月23日武汉市实施了封城措施，随之湖北省各地陆续开始封城，交通暂停了运营，大中小工厂开始关闭，很好地阻止了疫情传播，同时疫情措施也限制了人类的活动。从IQAir发布《2020年全球空气质量报告》可知，由于疫情封锁措施和人类行为的改变，全球空气总体上更加健康，中国86%的城市空气质量较上一年有所改善[7]。

2 模型设定

传统的回归模型是研究被解释变量的条件期望，即自变量x对因变量y的条件期望E（y|x）的影响。为了能更全面地描述解释变量对被解释变量在不同分位数上的影响，Koenker和Bassett[8]于1978年提出了分位数回归模型。其估计量的计算是基于一种非对称形式的绝对值残差最小化，它能够更加全面的描述被解释变量条件分布的全貌，而不是仅仅分析被解释变量的条件期望。与最小二乘法相比，分位数回归对误差项并不要求很强的假设条件，同时它的估计结果对离群值表现得更加稳健。

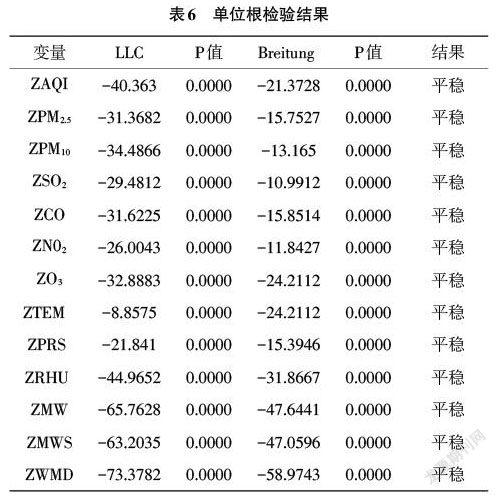
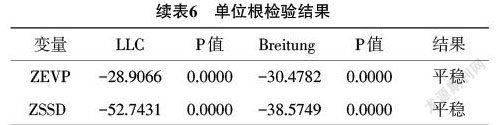
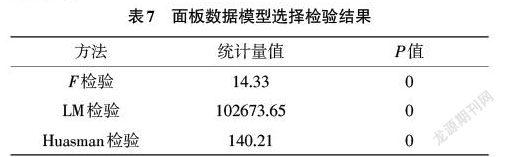
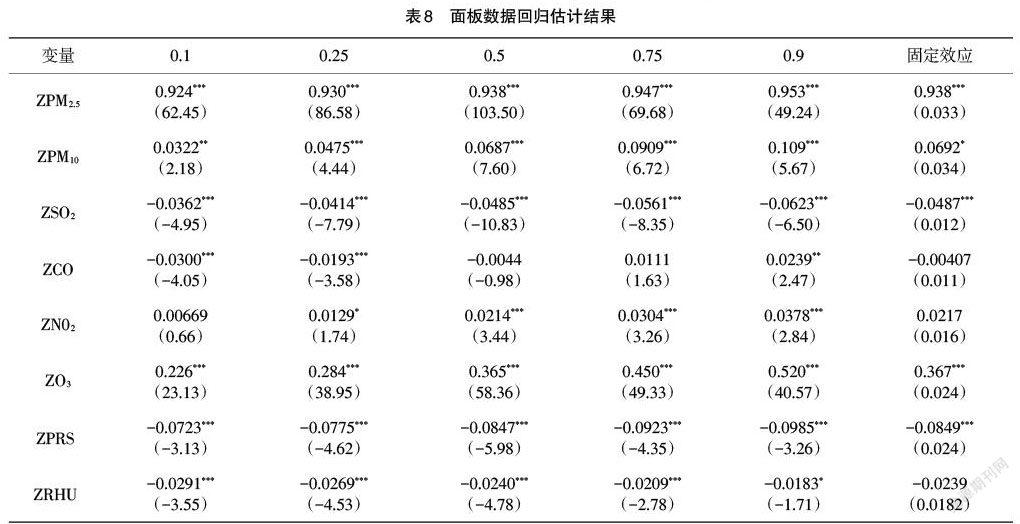
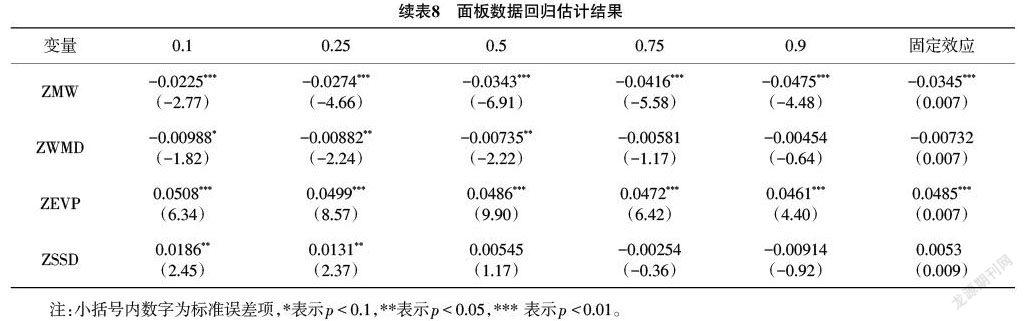
分位数回归的基本思想为：假定连续随机变量Y，其分布函数为[Fy=p（Y≤y）]，对于任意0

[Q（q）=F-1（q）=inf{y：F（y）⩾q}]

则其函数形式可表示为：

[yqxi=x'iβ（q）]

2004年，Koenker[9]提出了面板分位数模型，面板数据能够控制个体的异质性，保证结果的无偏性，同时面板数据可以从时间序列和截面两个维度提供更多的信息、变化以及更高的估计精度。将面板数据和分位数回归相结合，可以充分发挥面板数据的优点，在控制个体异质性的同时更好地分析自变量在不同分位点上对因变量条件分布的影响。其函数形式为：

[Qyitq∣xit=αi+xTitβ（q）]

其中[i=1，…，N;t=1，…，T];[yit]表示第[t]时期第[i]个个体被解释变量的观测值;[xit]则是解释变量的观测值，[αi]表示不随分位数[q]变化且不被其他变量控制的个体之间的差异。

将各市的数据整理成面板数据，为了衡量6种空气污染物和气象因素对AQI的影响，且保证量纲的一致性，对所有指标进行标准化处理，构建本文使用的面板数据模型如下：

[ZAQIit=αi+β1ZPM2.5it+β2ZPM10it+β3ZN02it+β4ZSO2it+β5ZCOit+]

[β6ZO3it+β7ZTEMit+β8ZPRSit+β9ZRHUit+β10ZMWit+β11ZMWSit+]

[β12ZSSDit+β13ZEVPit+β14ZWMDit+μit]

其中：[ZAQI it]表示第i个城市在第t时刻的标准化后的空气质量指数，[ZPM2.5it]，……，[ZWMD]分别表示第i个城市在第t时刻标准化后的[PM2.5]浓度…，以及标准化后的最大风向值。

3 面板分位数回归分析

3.1 多重共线性检验 多重共线性在建模过程中是普遍存在的，轻微的多重共线性问题对模型影响不大，一般不采取处理措施，当多重共线性问题较为严重时，要根据不同情况采取必要措施。多重共线性检验常用的方法有2种，一是相关性分析，若相关系数高于0.8，表明存在多重共线性;但相关系数值较低，并不能表示不存在多重共线性;二是vif检验，当vif的值高于10时，表明存在多重共线性;本文在已建立模型的基础上选择vif检验方法，结果如表5所示。从vif检验结果可知，所有变量值均在10以下，说明各变量间不存在严重的多重共线性问题。

3.2 面板单位根检验 为避免非平稳序列回归分析带来的伪回归问题，需要在采用面板分位数模型估计之前，对各变量进行面板单位根检验，即平稳性检验[10]。面板单位根检验主要有两大类检验方法：一类是基于同质面板数据的检验，假设各面板单位自回归系数均相同，如LLC检验、HT检验、Breitung检验;另一类是基于异质面板数据的检验，允许各面板单位自回归系数均不同，如IPS检验、Fisher-ADF检验和Fisher-PP检验[11]。由于本文所采用的数据时间维度大于横截面维度，也就是长面板数据，同时为防止单一检验可能造成的误差，故选择了LLC检验、Breitung检验检验2种检验方法进行单位根检验，由表6中检验结果可知，各变量均通过平稳性检验。

3.3 模型选择 为与传统面板回归模型的结果进行对比，首先构建传统面板回归模型。传统面板回归模型主要有3种形式：混合回归、固定效应和随机效应，一般采用F检验、LM检验和Hausman检验来确定应该选择何种模型[12]。各检验结果列于表7中，其中F检验的p值为0.000，表明在1%的显著性水平下，强烈拒绝原假设，认为固定效应模型要优于混合回归模型;LM检验的p值为0.000，同样在1%的显著水平下，拒绝原假设，认为随机效应优于混合回归;Hausman检验的p值也是0.000，故在1%的显著性水平下，拒绝原假设，则模型最终设定为固定效应。

进行面板分位数回归时，选取0.1、0.25、0.5、0.75、0.9等5个具有代表性的分位点，分别代表优、良、轻度污染、中度污染以及重度污染下的空气质量，因此可以了解到在不同等级的空气质量下，各因素对空气质量有怎样的影响。

3.4 回归结果分析 将湖北省11个城市的面板数据分别代入2种模型中，利用stata15.0分别进行面板数据固定效应和分位数回归估计，结果见表8。由于气象因素中平均气温和最大风速在固定效应模型以及分位数回归中均不显著，因此未列于表中。

从固定效应模型回归结果可知，在1%的显著性水平下，污染物指标中[ZCO]、[ZN02]未通过检验，说明在空气质量的平均水平下，[CO]浓度和[N02]浓度对空气质量的影响是不显著的;气象因素中，除了表中未列出的平均气温和平均风速外，变量[ZRHU]、[ZWMD]以及[ZSSD]的系数也未通过检验，由此说明相对湿度、风向及日照时长对空气质量的平均水平影响并不显著。在回归系数通过显著性检验的变量中，其中系数符号为正的有[ZPM2.5]、[ZPM10]、[ZO3]和[ZEVP]，对空气质量指数存在正向影响，说明[PM2.5]浓度、[PM10]浓度、[O3]浓度和空气相对湿度的增加会导致AQI的增加，因此会导致空气质量会变差;其中系数符号为负的变量有[ZSO2]、[ZPRS]和[ZMW]，说明[SO2]浓度、平均气压和平均风速对AQI存在负向影响，这3项指标值的增加对空气质量有一定的调节作用。污染物浓度是影响空气质量的主要因素，其中[ZPM2.5]的弹性系数最大，系数值高达0.938，其次是[ZO3]变量，系数值为0.367，可见[PM2.5]和[O3]浓度的增加会导致空气质量指数的大幅度提升。

从面板分位数回归结果可以看出：（1）变量[ZPM2.5]、[ZPM10]、[ZNO2]和[ZO3]的系数均为正，可知污染物中[PM2.5]、[PM10]、[NO2]和[O3]与AQI均呈正相关，并且这几项指标系数随着分位点的增加而增大，其中[NO2]在0.1分位点上并不显著，随着分位点的增加变得越来越显著，说明[PM2.5]、[PM10]、[NO2]和[O3]浓度的增加会导致空气质量变得更糟糕。（2）在1%的显著性水平下，[ZSO2]的系数在各分位点上均通过了显著性检验且值为负，并随着分位点的不断增加其系数却逐渐变小，说明在空气质量优良时，一定浓度的[SO2]可以起到调节空气质量的作用。（3）[ZCO]的系数存在一个由正变负的过程，在0.1、0.25和0.5位点上，[ ZCO]的系数值为负，在 0.75和0.9分位点上系数为正，说明[CO]对AQI具有双重影响，当空气质量优良时，一定浓度的[CO]是正常的，但是其浓度若超过一定的范围会加重空气污染程度。（4）在气象因素中，变量[ZPRS]、[ZRUH]、[ZMW]和[ZWMD]在各分位点上的系数值为负，说明平均气压、相对湿度、最大风速和风向与AQI呈负相关，其值的增加会使AQI减小，对空气质量的影响是积极的，其中风向在0.1～0.75分位点上对AQI影响显著。（5）在1%的显著性水平下，[ZEVP]的系数在各分位点上均通过了显著性检验且系数值为正，从0.1～0.9分位点上，其值是渐渐变小的，说明大型蒸发量与AQI呈正相关并且对空气质量的影响越来越弱。（6）观察变量[ZSSD]可知，在0.1～0.9分位点上，其系数是存在一个由正变负的过程，在0.1和0.25分位数上日照时长对AQI有着正向作用，说明一定的日照时长对空气質量是有利的，在0.5～0.9分位点上，日照时长对空气质量的影响是不明显的。

4 结论

本研究选取2018—2020年湖北省11个城市的面板数据，利用面板分位数回归的方法实证分析了6种污染物浓度和8种气象因素对AQI的影响，采用固定效应回归模型进行对比分析，主要结论如下：

（1）根据湖北省11个城市空气质量的描述性分析，空气质量最好的是恩施，其优良天数最多，空气质量相对其他几个城市最差的是襄阳市，其次是荆门、宜昌和武汉。根据时间趋势进行空气质量分析，可知2019相对于2018年来看，湖北省空气质量整体状况均呈下降趋势，空气污染天数有所增加，2018—2020年湖北省整体空气质量上升。

（2）在固定效应回归模型中，[ CO]、[N02]、平均气温、平均风速、相对湿度、风向以及日照时长对空气质量的影响不显著，其余变量均显著，其中[PM2.5]、[PM10]、[O3]和相对湿度与AQI呈正相关，这些变量值的增加将会导致空气质量进一步变差，[SO2]、平均气压和最大风速与AQI呈负相关，[SO2]浓度、平均气压和最大风速的增加对空气质量起着一定的调节作用。

（3）在面板分位数回归中，[ PM2.5]、[PM10]、[NO2]、[O3]和大型蒸发量与AQI均呈正相关，其中[PM2.5]、[PM10]、[NO2]和[O3]的系数随着分位数从0.1～0.9的变化而增大，大型蒸发量的系数值随着分位数的增加缓慢减小;[SO2]、平均气压、相对湿度、最大风速和风向与AQI呈负相关，除了最大风速的系数值随着分位数的增加而增加，其他變量均呈减小趋势，同时风向只在0.1～0.5分位点上对AQI有显著影响，其他变量在所有分位点上均显著;[CO]对AQI具有双重影响，随着分位数的增加，其系数符号由负变正，且只在低分位点处对AQI有显著影响;变量[ZSSD]的系数是由正变负的一个过程，同样只在低分位点上对AQI有显著影响，在高分位点处对空气质量的影响并不显著。

参考文献

[1]2019年全球卫生面临的10项威胁[EB/OL].（2019-1-10）.[2021-03-23].https：//www.who.int/zh/news-room/spotlight/ten-threats-to-global-health-in-2019.

[2]徐萌，张春鑫，徐林，等.毕节市区大气污染特征及影响因素分析[J].安全与环境工程，2018，25（05）：64-71.

[3]湛社霞，匡耀求，阮柱.基于灰色关联度的粤港澳大湾区空气质量影响因素分析[J].清华大学学报（自然科学版），2018，58（08）：761-767.

[4]付倩娆.基于多元线性回归的雾霾预测方法研究[J].计算机科学，2016，43（S1）：526-528.

[5]晏振，田茂再.基于分位回归的北京市PM2.5的影响分析[J].统计与决策，2015（17）：103-105.

[6]许燕婷，刘兴诏，王振波.基于AQI指数的中国城市空气质量时空分布特征[J].广西师范大学学报（自然科学版），2019，37（01）：187-196.

[7]戈达赫.《2020年全球空气质量报告》[EB/OL].（2021-3-16）.[2021-3-23]. https：//www.iqair.cn/cn/blog/press-releases/covid-19-reduces-air-pollution-in-most-countries.

[8]Koenker R，Bassett G. Regression Quantiles[J].Econometrica，1978，46（1）：33-50.

[9]Koenker R. Quantile regression for longitudinal data [J].Journal of Multivariate Analysis，2004（1）：74-89.

[10]陈强.高级计量经济学及Stata应用[M].北京：高等教育出版社，2013.

[11]赵强，曹炜婷.基于面板数据分位数回归的商品住宅价格影响因素分析[J].山东财经大学学报，2017，29（05）：61-69.

[12]郑林昌，张亚楠，李泽阳.河北省城市空气污染物对PM（2.5）浓度值是否有影响——基于城市空气质量数据的面板分位数回归分析[J].统计与管理，2020，35（01）：70-73. （责编：张宏民）