基于灰色动态模型群的衡水市居民年用水量预测

吴永强，李明凯,2，唐中楠，王书盛，王锦涛

1.河北建筑工程学院市政与环境工程系

2.河北省水质工程与水资源综合利用重点实验室

水资源是生态环境建设和社会可持续发展的重要基础。随着衡水市城市规模的持续扩大，城市常住人口的不断增加，用水量增长迅速，供水的复杂性和不确定性日益凸显，难以对城市未来需水量和供水量进行准确把握。因此，准确预测分析城市供水量和需水量，对有效预防供水过剩导致的水资源浪费和供水不足导致的用户缺水等问题具有重要意义。

用水量预测研究是水资源规划和供水调度的重要基础环节，只有准确合理地预测城市用水量，才能为城市水资源规划调配提供合适的参考依据。秦欢欢等[1]采用系统动力学模型，考虑影响用水量等诸多因素，设定了4 种不同城市发展情景，对北京市用水量进行预测分析。宋帆等[2]建立灰色关联—集对聚类预测模型，对吉林省进行短期用水量预测。在城市需水量预测方法中深度学习法逐渐被应用。如牟天蔚等[3]以深度学习框架为基础建立了小波深度信念网络（SW-DBN）时间序列模型，并应用该模型对城市日需水量进行预测，与BP 神经网络预测模型相比，该模型可以对大样本进行更加准确的预测，且提高了城市日用水量预测精度。

灰色模型预测用水量所需数据少，对短中期用水量预测有较好效果。相比其他预测模型显示出一定的优势，但当原始数据离散大时精度差[4]。基于灰色模型的优缺点，许多学者对灰色预测模型进行优化改进研究。如柳烨等[5]将微粒群算法优化结合GM(1,1)模型对城市用水量进行预测；任晔等[6]使用灰色神经网络组合模型对年降水量进行预测；赵宇哲等[7]采用灰色振荡序列GM(1,1)模型对城市用水量进行预测；唐万梅[8]提出了一种新型的灰色支持向量机预测模型；刘献等[9]采用马尔科夫链修正的残差灰色模型对生活用水量进行预测；杜懿等[10]在前人的研究基础上进行概括总结，综合预测方法，对比不同预测模型精度并应用于广西省年用水量预测；白鹏等[11]以京津冀为研究区域，对比了灰色神经网络法、年增长率法和自回归模型法，并采用灰色神经网络法进行京津冀地区2019—2025 年的年用水量预测；刘呈玲等[12]建立了用弱化算子改进后的灰色GM(0,N)模型，并对太湖流域2016—2020 年用水总量进行预测；唐晓灵等[13]以关中平原城市群为研究区域，应用网络SBM-DEA 模型定量测度2005—2016 年工业用水效率，并将灰色预测法与定额比较法相结合，对未来5 年工业节水潜力进行预测，研究工业经济与水资源之间的相关关系。

灰色系统分析方法在信息不完整或不完全的情况下具有良好的适用性[14]，其中GM(1,1)模型常用于城市用水量预测。但是单一的灰色模型在预测过程中会受到不稳定因素影响，使预测结果与实际值偏差较大。利用灰色动态模型群构造多个单一灰色GM(1,1)，并求取平均值作为预测结果，可较好地弥补单一的灰色模型不稳定因素对预测结果影响的缺陷。笔者以衡水市为研究区域，首先基于原始数据建立灰色动态模型群对衡水市居民年用水量进行预测，然后对不符合精度的GM(1,1)模型进行残差修正，应用修正后的灰色模型群对衡水市2020—2030年居民用水量进行预测，最后将残差修正后的灰色模型群的预测相对误差分别与5 个单一GM(1,1)模型的预测相对误差进行比较分析，以检验模型性能，旨在为衡水市未来居民用水量预测提供准确可靠的手段。

1 灰色动态模型群构建

1.1 GM(1,1)模型原理

GM(1,1)模型是灰色系统理论中常用的模型，在水量预测方面应用较为广泛。该模型是通过对原始数据进行累加，将累加后的计算结果通过1 个一阶变量的微分方程计算出来，最后将模型计算值进行累减后得到预测值[15]，其建模过程如下。

对于一个初始的时间序列X(0)(k)为：

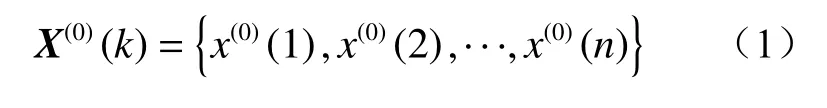
式中：X(0)(k)为非负级数的原始数据；n为数据个数；k为不同时间点的数据编号，k取1，2，···，n。

对X(0)(k)做累加，可以得到：

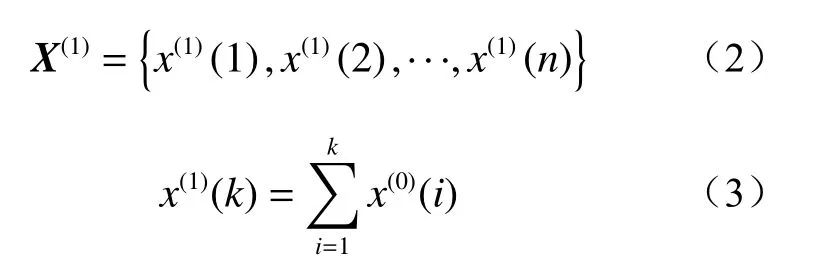
则GM(1,1)模型的微分方程如下：

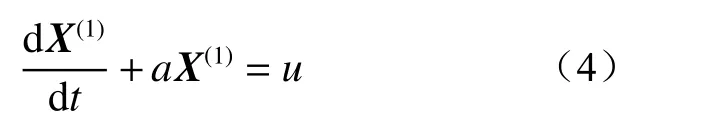
式中a、u为待解系数，分别称为发展系数和灰色作用量。a、u采用最小二乘法确定。

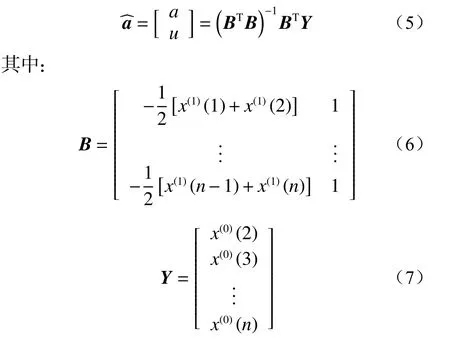
式中：B为累加生产矩阵；Y为数据向量。

灰色预测模型可以通过a和u得到：

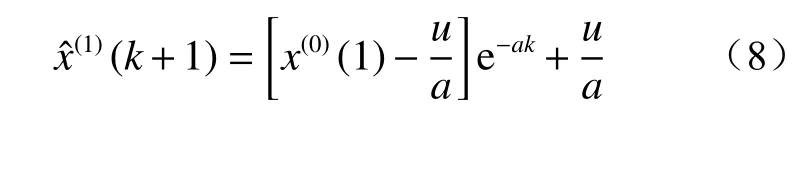
将预测模型计算得到的结果通过累减，即可求得模型的预测值：

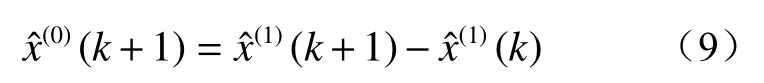
1.2 GM(1,1)动态模型群的建立

依据单个GM(1,1)模型的建模理论，规定GM(1,1)动态模型群建模采用的数据序列x(0)(k)的数据个数需要大于4 个。假设原始数据序列x(0)(k)中有n个数，含有原始数据系列中最后一位数的组合数为n-3，则可建立起n-3 个子模型组成的灰色预测模型[16-17]。

以X(0)(n-3)，X(0)(n-2)，X(0)(n-1)，X(0)(n)建立的第1 个模型为：

以X(0)(n-4)，X(0)(n-3)，X(0)(n-2)，X(0)(n-1)建立的第2 个模型为：

以X(0)(1)，X(0)(2)，···，X(0)(n)建立的第n-3 个模型为：

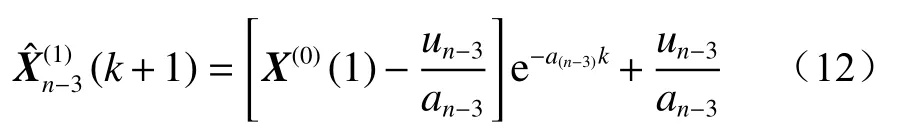
利用上述单一GM(1,1)模型分别进行预测，再以不同时间序列的各单一GM(1,1)模型预测结果的平均值作为各时刻的预测值。

1.3 灰色模型检验

针对建立的单一GM(1,1)模型，采用残差检验的方法进行检验，根据各单一灰色GM(1,1)模型精度等级，确定灰色动态模型群的精度等级。采用残差检验以及后验差检验法来对建立的灰色预测模型进行精度检验[18]。

1.3.1灰色模型残差检验

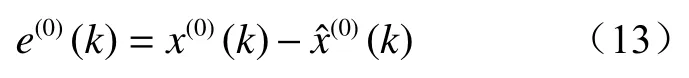
相对误差(q)计算公式为：

1.3.2灰色模型后验差检验法

通过灰色模型后验差检验，可以检验灰色模型群中各单一GM(1,1)模型的拟合程度。

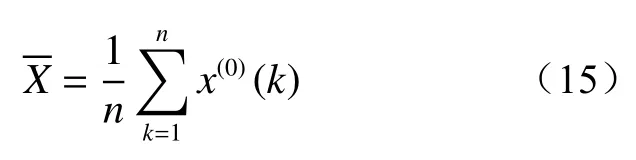
模型方差（S1）计算公式为：

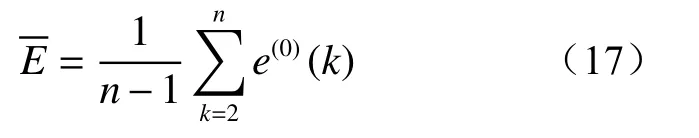
模型残差方差（S2）计算公式为：

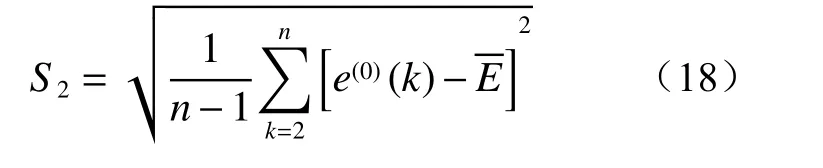
模型后验差比值（C）计算公式为：

模型的小误差概率（P）计算公式为：

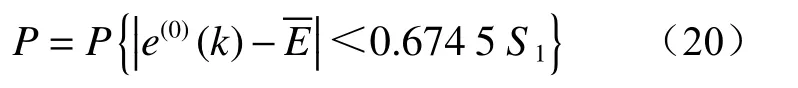
GM(1,1)模型精度由C、P2 项指标共同确定。其检验精度指示如表1 所示。当后验差检验精度不合格时，可通过建立残差模型来对原模型进行修正[19-21]。

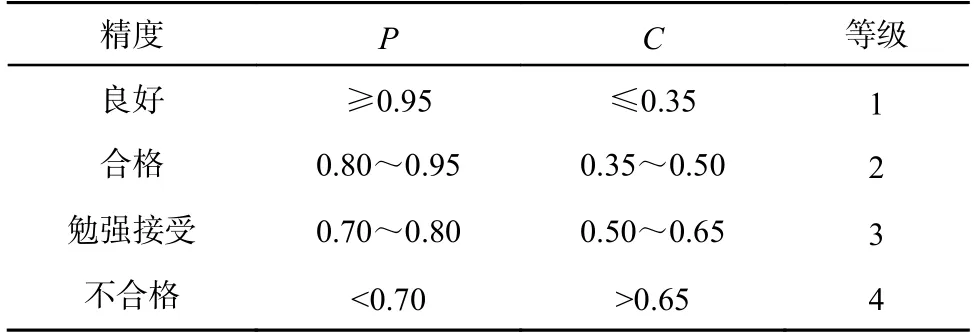
表1 检验精度指示表Table 1 Check accuracy indicator

1.4 灰色模型残差修正

灰色模型对数据样本序列为非负，符合指数形式的变化规律且变化速度相对平缓，具有良好的预测效果，但是当原始数据样本变化速度大或者波动较大的情况下，灰色模型的预测效果达不到理想状态。因此需要建立残差修正灰色模型以有效提高GM(1,1)模型预测精度。

依据1.1 节得到的原始数据x(0)(k)和预测值xˆ(0)(k)建立一阶残差序列：

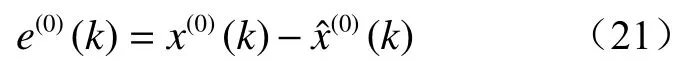
以一阶残差序列建立GM(1,1)模型：

式中：E(0)(1)为一阶残差初始的时间序列；ae、ue为待解系数，分别称为发展系数和灰色作用量，可用最小二乘法求得。

将一阶残差序列建立的GM(1,1)模型以及初始数据序列建立的GM(1,1)模型进行叠加，得到修正后模型：

将残差修正模型计算得到的结果通过累减，即可求得模型的预测值

将残差修正模型引入GM(1,1)模型，灰色模型增加了对预测结果准确度的评价，并对预测结果进行较为合适的修正，降低了因原始数据样本变化速度大或者波动较大的情况下导致的误差偏大，提高了灰色模型预测的合理性和预测精度[22-23]。灰色模型精度要求见表2。

表2 灰色模型精度要求Table 2 Grey model accuracy requirements

2 实例应用

2.1 研究区域概况

衡水市位于河北省东南部，地处河北冲积平原，地势自西南向东北缓慢倾斜，总面积为8 815 km2。衡水市水资源严重匮乏，人均水资源量未达到河北省平均水平的40%。随着衡水市社会经济的快速发展、人民生活水平的不断提高以及用水人数的增加，对水资源的需求量也越来越大，水资源矛盾日益凸显。衡水市地表水已无法满足当地的用水量需求，导致深层地下水超采严重，逐渐形成“冀枣衡”漏斗区。随着漏斗中心水位的逐年下降，漏斗区的面积也在逐年扩大[24-25]。而未来随着用水人数增长速度的加快，居民用水量预计会明显增长。因此，对衡水市居民用水量进行合理预测，并为供水调度和水资源优化配置提供参考非常必要。根据《中国城市建设统计年鉴》[26]得到2007—2019 年居民年用水量数据，如表3 所示。

表3 2007—2019 年衡水市居民年用水量Table 3 Annual RWC in Hengshui City from 2007 to 2019 万 m3

2.2 灰色动态模型群的建立与检验

利用2007—2014 年衡水市居民年用水量数据进行模型率定，建立5 个单一灰色预测模型：模型1采用2007—2014 年用水量数据；模型2 采用2008—2014 年用水量数据；模型3 采用2009—2014 年用水量数据；模型4 采用2010—2014 年用水量数据；模型5 采用2011—2014 年用水量数据。再利用所建立的灰色动态模型群对2015—2019 年用水量数据进行模拟预测，将预测值与实际数据进行对比[27]，并运用残差法对模型进行精度检验，结果见表4。由表4 可看出，模型1～模型5 的精度等级均为合格以上，满足模型建立的精度要求。

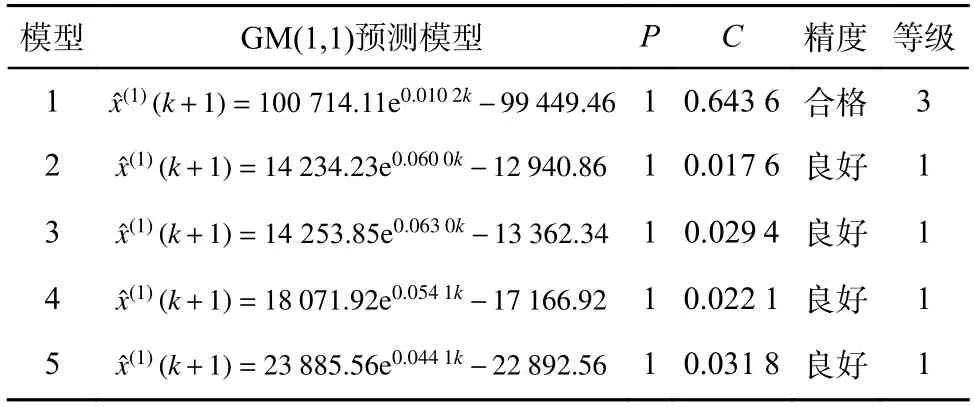
表4 GM(1,1)模型群及残差检验Table 4 GM(1,1) model group and residual test

2.3 用水量预测灰色模型残差修正及预测结果分析

根据表4 建立的灰色动态模型群对衡水市2015—2019 年居民年用水量进行预测，将预测结果与实际用水量进行比对，得到相对误差和残差（表5）。由表5 可知，衡水市2015—2019 年居民用水量的预测值和实际值相对误差分别为-2.65%、-20.04%、-27.18%、-20.98%、-17.52%，2016—2018年误差绝对值均大于20%，不符合灰色模型预测精度要求。因此，需要对该灰色动态模型群进行残差修正。

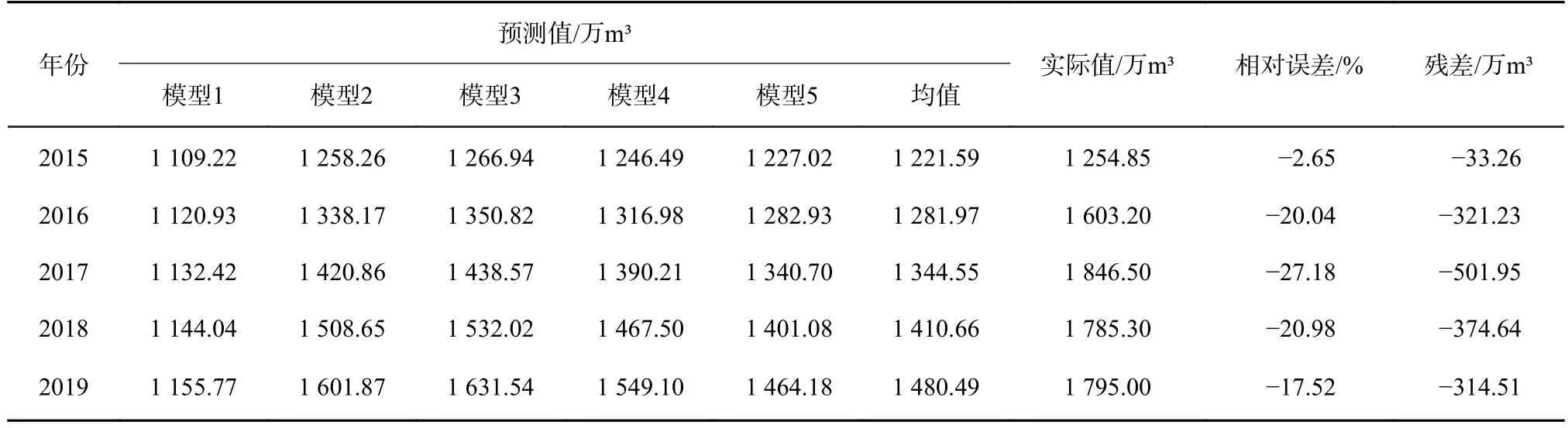
表5 残差修正前2015—2019 用水量预测值与实际值对比Table 5 Comparison of projected and actual water consumption data from 2015-2019 before residual correction

对5 个单一GM(1,1)模型分别以一阶残差序列建立GM(1,1)模型，得到修正预测模型（表6）。利用表6 模型对衡水市2015—2019 年居民年用水量进行预测，将残差修正后的用水量预测值与实际值进行对比，结果如表7 所示。由表7 可知，残差修正后的灰色动态模型群的预测相对误差绝对值分别为7.17%、-11.98%、-19.72%、-12.96%、-9.43%，相对误差均小于20%，符合灰色模型的中期预测相对误差的范围。残差修正前后居民年用水量的预测值与实际值及相对误差如图1 所示。由图1(b)可知，实际用水量趋势与预测值趋势大致相似且满足精度要求。5 个单一灰色模型预测的相对误差与灰色动态模型群预测的相对误差如图2 所示。由图2 可知，2015—2019 年残差修正后灰色动态模型群的预测相对误差相比于单一灰色模型的预测相对误差整体偏低。综上可得，残差修正后的灰色动态模型群对衡水市居民用水量预测更加准确合理。因此残差修正后的灰色动态模型群具有良好的预测效果，可应用于未来衡水市居民用水量预测。

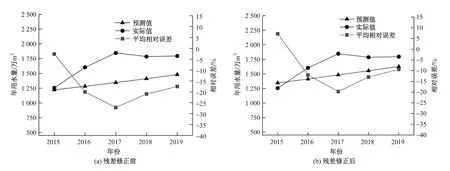
图1 2015—2019 年衡水市居民年用水量预测值与实际值对比及相对误差Fig.1 Comparison and relative error between predicted and actual annual RWC of Hengshui City from 2015 to 2019

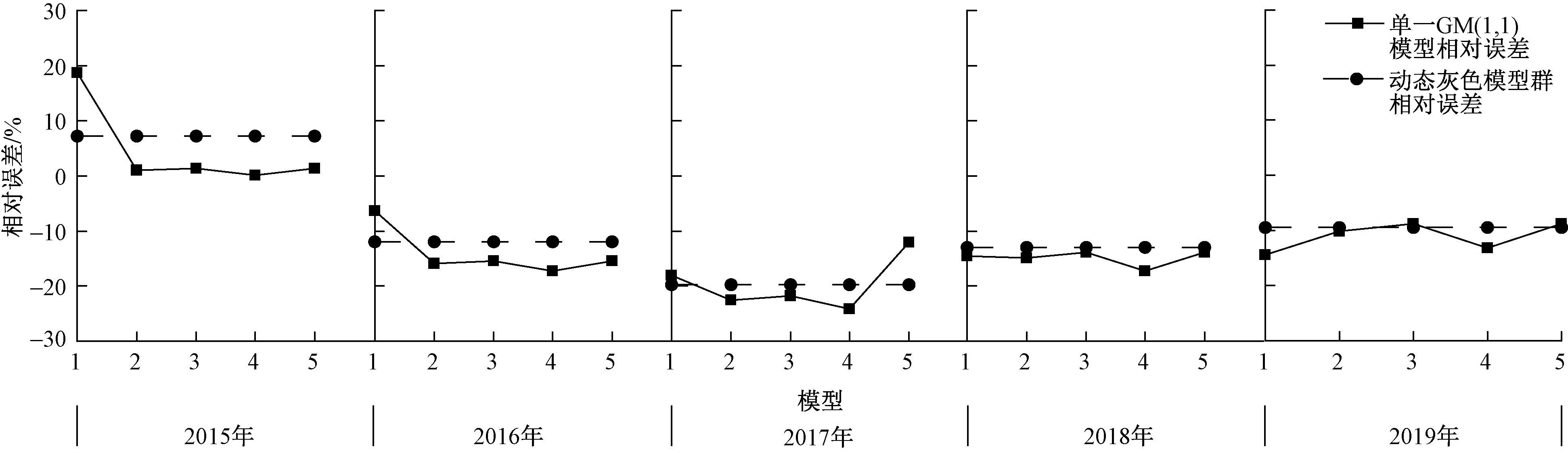
图2 2015—2019 年衡水市居民用水量灰色动态模型群误差检验Fig.2 Error test of dynamic gray model group of RWC in Hengshui City from 2015 to 2019

表6 GM(1,1)残差修正后预测模型群Table 6 GM(1,1) residual-corrected prediction model group

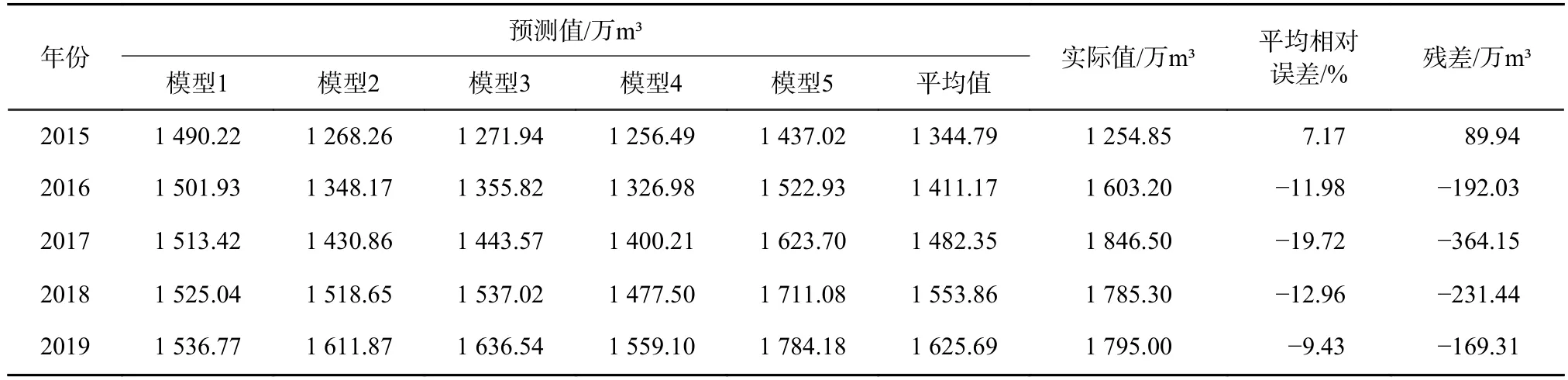
表7 残差修正后2015—2019 用水量预测值与实际值对比Table 7 Comparison of predicted and actual water consumption data for 2015-2019 after residual correction

2.4 衡水市居民未来用水量趋势预测分析

将表6 灰色动态模型群应用于衡水市2015—2030 年的年用水量预测，结果见表8，衡水市居民用水量变化趋势见图3。由表8 和图3 可知，未来衡水市居民用水量将继续保持增长趋势，2020 年衡水市居民用水量预计增至1 795.44 万m³，2030 年预计增至2 862.21 万m³，这与衡水市居民生活水平的提高和用水人数的增长趋势相符合。

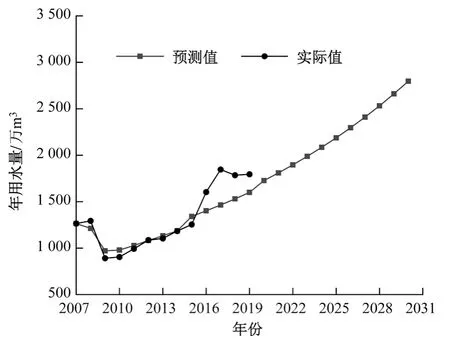
图3 衡水市居民用水量预测拟合效果及未来用水量预测Fig.3 Prediction and fitting effect and change trend of RWC in Hengshui City in the future

表8 衡水市居民年用水量预测结果Table 8 Projected annual water consumption of Hengshui residents 万 m3

3 结论

（1）基于衡水市居民用水量数据建立灰色动态模型群，利用该模型群对衡水市2015—2019 年居民用水量进行预测，其相对误差分别为7.17%、-11.98%、-19.72%、-12.96%、-9.43%，与单一灰色模型相比，灰色模型群的整体拟合程度更好，预测结果更精确，且降低了以往单一GM(1,1)模型建立过程中不稳定因素对预测结果的影响。

（2）应用建立的灰色模型群对2015—2019 年衡水市居民用水量进行预测并与实际值进行对比，发现预测值的相对误差大于20%，不符合灰色模型预测精度。对5 个单一GM(1,1)模型进行残差修正并建立了GM(1,1)残差修正后预测模型群，预测值的相对误差均小于20%，符合灰色模型预测精度。应用该模型群对衡水市未来10 年居民用水量进行预测，结果表明用水量呈上升趋势，且当地居民用水量预计在2030 年达到2 862.21 万m³。

（3）灰色模型在数据较多的情况下可以更稳定地预测居民用水量。该模型可用于其他与水有关的应用，如由于降水和季节变化引起的水位变化等。此外，该模型也可根据不同地区供水和用水数据的提供情况，对不同区域、不同用水类型及不同季节用水量进行预测。