平房仓中稻谷密度的时空分布值及堆高沉降特性研究
程绪铎, 陈 雪, 唐福元,邵小龙
(南京财经大学食品科学与工程学院;江苏省现代粮食流通与安全协同创新中心,南京 210046)
稻谷储藏在平房仓中,稻谷堆受到重力及仓壁对稻谷堆作用力,产生压应力和切应力[1]。稻谷籽粒松软,籽粒间的孔隙大,各处的应力作用导致稻谷堆产生形变和体积压缩,稻谷堆密度增加。平房仓内稻谷堆的应力分布是不均匀的,所以稻谷堆的密度分布也是不均匀的,即平房仓中稻谷堆密度是空间的函数。稻谷堆是黏弹塑性体,在应力的作用下,稻谷堆持续变形,稻谷块的体积持续减小,密度持续增大,即平房仓中稻谷堆密度是时间的函数。
粮食储藏数量检查是粮食库存检查的一项重要内容,即通过一定的手段获取粮仓中所储存粮食的数量,主要包括称重法和体积密度法[2]。称重法工作量大、效率低,在大规模的库存检查中很难广泛使用。体积密度法是指通过测量粮堆的体积和平均密度计算粮仓中粮食数量的检查方法。现有的体积密度法是使用粮食的表层密度乘以修正系数来获取粮堆的平均密度,修正系数是凭经验给出的,此方法测定粮仓中粮食的数量误差较大。
陈得民等[3]通过在粮仓底部安装压力传感器,测定粮仓底部的压力分布,从而估算出粮堆的总重量,此方法成本高且只能给出粮堆总重量不能给出粮仓内粮堆密度分布值。程绪铎等[4]开发了一个分层压缩模型来预测平房仓中的粮层密度和压应力分布。陈雪等[5]选定修正剑桥模型作为小麦堆的应力与应变关系本构方程,使用有限元方法计算出平房仓中小麦堆密度的三维分布值。但这2种方法只能预测装粮后瞬时(储藏时间为零)的粮堆密度分布值。
本文将使用粮食回弹模量仪测定出稻谷堆的压缩密度与最大主应力(竖直压应力)及储藏时间的关系模型。求解稻谷堆修正剑桥模型计算出装粮后瞬时平房仓中稻谷层的竖直压应力分布值。由平房仓中稻谷堆各层的竖直压应力和稻谷堆的压缩密度与最大主应力(竖直压应力)及储藏时间的关系模型计算出平房仓中稻谷层的密度与粮层深度及储藏时间的关系模型。以期预测某一储藏时间的平房仓中稻谷堆的密度分布值,从而由密度分布值计算出储粮总质量。
1 材料与仪器
1.1 材料
稻谷品种为镇稻19号,含水率为12.93% w.b.,堆密度为536.7 kg/m3。
1.2 仪器
TSZ-6A应变控制式三轴仪,LKY-1型粮食孔隙率测定仪,LHT-1型粮食回弹模量测定仪。
2 实验方法
2.1 稻谷堆的压缩密度与储藏时间及最大主应力(竖直压应力)的关系测定
将稻谷装入LHT-1粮食回弹模量仪的圆筒中,顶部加载荷,圆筒中的稻谷受到压缩,处于主动应力状态,即竖直压应力为最大主应力,水平压应力为最小主应力。在粮仓中粮堆受到重力与仓壁对粮堆的压力及摩擦力,重力是主动力,粮堆内部产生的应力处于主动应力状态,即竖直方向主动的压,水平方向被动的压,最大主应力线是垂直的(在接近仓壁处稍有弯曲)[6],因此,粮食回弹模量仪圆筒中的应力状态与平房仓中各处的稻谷块应力状态相似。本试验对回弹模量仪的圆筒中的粮堆施加不同的顶部压力并压缩不同的时间来模拟平房仓中不同储藏时间各稻谷块的应力状态。本文用圆筒中稻谷堆的平均竖直压应力等于平房仓中某一稻谷块的竖直压应力。
2.1.1 装样筒内粮堆平均竖直压应力
其次,核心作者都为前十位核心研究机构的专职教师或研究员,职称级别较高,教授、副教授职称级别的作者占比超过90%,如马耀峰、保继刚、吴必虎等。同时,各大高校青年学者的学术研究能力正在增强,如黄潇婷、张佑印等,形成了持续发力的学术研究氛围。此外,核心作者的学科专业素养较高,拥有高质量的独立研究团队,大多采取两人、三人合作研究的方式,初步形成了旅游者行为研究的高级别核心作者群。未来学界应不断突破地理空间的限制,推动跨区域、多主题的学科交流与合作,形成规模化的学术合作网络圈层。
采用微元层法对装样筒内粮堆进行受力分析,假设装样筒内径为Rc,样品压缩高度为H,取距离粮面深度为y,厚度为dy的微元层进行受力分析,见图1[6]。

图1 回弹模量仪装样筒中的微元受力图
由稻谷薄层的竖直方向受力平衡可得:
(1)
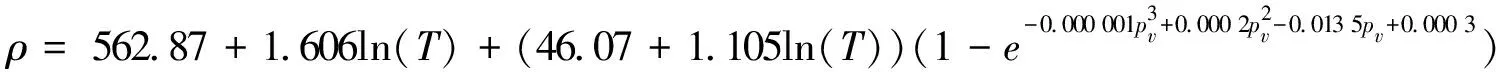
对式(1)进行积分得:
渗沥液的复氧方式包括自然复氧、利用曝气头进行微曝气、喷淋曝气和跌水曝气等。工艺中在矿化床床内设置通气管进行自然或强制复氧,表面种植绿色植物有益于根系对内部复氧。
将回弹模量仪测定的稻谷压缩密度与式(12)计算出的稻谷堆密度对比,见图2。
(2)
对式(2)进行二次积分,得到稻谷堆所受平均竖直压应力pv为:
(3)
式中:p0为稻谷堆顶部压力/kPa;H为压缩后圆筒中稻谷堆高度/m。
2.1.2 装样筒内粮堆密度
对于Ⅱ~Ⅳ期患者除使用放疗外理想的肿瘤细胞减灭术联合化疗非常重要。畸胎瘤虽为生殖细胞肿瘤,但对于生殖细胞肿瘤敏感的PEB(顺铂、依托泊苷、博莱霉素)方案不是最佳化疗方案。成熟畸胎瘤鳞变术后辅助治疗与宫颈癌类似,可用鳞癌敏感的紫杉醇和铂类化疗[18],但MCT鳞癌变放疗效果与宫颈癌相比效果较差[19]。也有文献报道术后辅助放化疗对改善存活率意义不大且放疗影响患者生育能力[20],故可不主张对有生育要求的患者进行盆腔外放疗。Ito等[21]提出碳离子放射治疗治疗可视为治疗复发性TMT的一种新方法。对于复发性MCT鳞癌变患者进行碳离子放射治疗治疗可缩小肿瘤体积,延缓患者生存期。
装样筒内粮堆密度由式(4)计算。
根据JLZ2X1/F2A-1660/95-492型1 660 mm2大截面碳纤维导线(以下简称1 660 mm2导线)的半硬铝型线铝股和芯棒特点,采用仿真分析方法,比较了夹嘴长度分别为350,325,275 mm时导线的应力状况,从而确定适用于1 660 mm2导线的卡线器夹嘴长度,通过减小夹嘴长度对卡线器进行减重优化设计。
(4)
式中:m为稻谷堆的质量/kg。
修正剑桥模型的总应变包括体积应变εv和剪切应变εs,总应力包括广义剪切力q和平均主应力p。稻谷堆修正剑桥模型为:
虽然示范性教学是比较古老的教学模式,但对于成人在职培训中,多以更深入的理论教学为主,较少以示范性教学为主导的教学模式,但就本专科护士培训的实践证明,较好的范例对学员有很好的指导和启迪作用,使学员能够很快适应这种高效的短期培训,学习起来事半功倍,取得良好的效果。
装样:装样前称重,并测量样高。将样品均匀装入装样筒,并将样品表面铺平,放置传压板,并使传压板上表面与装样筒上端齐平。
杠杆调平:保证横梁杠杆垂直,将平衡锤转动调整杠杆至水平位置,M16螺母固定平衡锤。
将传压螺钉转动使其接触传压板,调整位移传感器的触头位置,将百分表调零。
对6个回弹模量仪加载不同的顶部压力,分别为50、100、125、150、175、200 kPa。
选定不同的时间间隔,记录时间与样品高度。
随着时间的推移,样品高度减小,导致杠杆向下倾斜。通过转动调平手轮,使杠杆一直保持水平,消除杠杆倾斜对加载精度的负作用。
2.1.4 稻谷堆压缩密度与储藏时间及最大主应力(竖直压应力)关系模型
首先,思政课教师的思想激励作用。“工匠精神培育的最佳时机就在高职生入学的开始一二年,这段时间也正是公共必修思政课的开课时期,把工匠精神的培育有效地融入高职思政教育必然有助于增加具有工匠精神人才的有效供给,为我国制造业的升级转型培养更多具有高级职业精神和高尚爱国主义情操的高素质人才。[5]”思政课要有针对性,能够解决学生在学习生活中的困难和疑虑,至少能给学生一种直面问题的思路和方法。学生在专业的学习上会遇到各种各样的困难,思政课教师要从思想上发挥答疑解惑的作用,引导学生去面对困难,用勇气解决困难。这是培养学生工匠精神必须具备的思路。
ρ=F(pv,T)
(5)
式中:T为稻谷堆压缩时间/h。
2.2 平房仓中稻谷的竖直压应力与深度关系的测定
2.2.1 稻谷堆修正剑桥模型
为了表征松软土壤的应力与应变关系,Roscoe等[7]提出了修正剑桥模型(Modified Cam Clay)。修正剑桥模型将总应变分为剪切应变与体积应变,总应力分为平均正应力与剪切应力,适合求解在外力作用下松软土壤堆中的应力与应变。稻谷堆孔隙大,籽粒松软,它的结构与松软土壤相似。Du等[8]研究了稻谷堆修正剑桥模型的模型参数,并使用修正剑桥模型研究稻谷堆的变形与压缩,修正剑桥模型的计算结果与实验结果是一致的。因此,本文选择修正剑桥模型求解平房仓中稻谷堆的应力与应变。
2.1.3 稻谷堆加压实验方法
(6)

2.2.2 稻谷堆的修正剑桥模型参数的测定
针对网络安全的建议,个人用户账户信息使用不同的加密算法,如MD5.电话功能使用虚拟电话。将数据经行加密处理。虽然这不能100%的保证数据的安全,但是可以一定程度上降低安全信息泄露的可能性。
使用应变控制式三轴仪测定修正剑桥模型参数M、λ、κ、υ,使用粮食孔隙率测定仪测定参数e0[8-10]。
2.2.3 平房仓中稻谷的竖直压应力与深度关系的确定
使用有限元软件ABAQUS求解稻谷堆修正剑桥模型得到平房仓中竖直压应力的三维分布值,由三维分布值计算出各粮层平均竖直压应力。
使用修正剑桥模型计算出装仓后瞬时平房仓中稻谷各层竖直压应力及各处的深度。将装仓后瞬时粮仓中各处粮块应力状态与回弹模量仪圆筒中稻谷堆(压缩时间为10 min)的相同应力状态对应起来。随着储藏时间的增加,粮仓中各处粮块体积应变与对应的圆筒中稻谷堆体积应变相同。这样,就能得到平房仓中稻谷各层的密度随深度及储藏时间变化的关系。因此,计算出稻谷装仓瞬时平房仓中稻谷堆竖直压应力与深度关系是计算平房仓中稻谷各层的密度随深度及储藏时间变化关系中的关键一步。
2.3 平房仓中稻谷堆密度与粮层深度及储藏时间关系的确定
稻谷储藏在平房仓中,稻谷堆持续受到压应力作用,稻谷堆体积逐渐减小,粮堆各处的密度逐渐增加。
将平房仓中稻谷堆分为质量相等的n层,由限元软件ABAQUS求解稻谷堆修正剑桥模型得出稻谷装仓后瞬时(储藏时间为零)各粮层平均竖直压应力。
随着储藏时间的增加,各粮层平均竖直压应力保持不变。不同储藏时间各粮层的密度值由式(5)确定。
不同储藏时间各粮层的厚度及深度由各层的密度与质量确定。
由不同储藏时间各粮层的深度与密度值拟合出平房仓中稻谷堆密度与粮层深度及储藏时间关系模型为:
宁夏青龙管业股份有限公司是中国预应力钢筒混凝土管质量联盟理事长单位,是一家致力于高品质管道研发、设计、生产、安装和服务于一体的专业化管道制造商、城市基础设施建设商和运营商。多年来,青龙管业在PCCP管道的质量控制、技术进步、工艺改良等方面进行了不懈努力,为我国PCCP行业的发展作出了突出贡献,在南水北调中线工程天津段、河北段、河南段的管材制造任务中均有出色表现,获得了承建方的一致好评与奖励。
ρ=F(h,T)
(7)
式中:h为平房仓中稻谷层深度/m。
隧道沉降一般采用注浆加固的治理措施,即在盾构隧道下卧层形成刚度大于原状土的加固体。由于盾构隧道纵向是环环相接的柔性结构,在注浆过程中需尽可能减小对地层的扰动,确保每环内注浆引起的附加横向应力和横向变形均在允许范围内,并对地层沉降具有较好的补偿效果。
2.4 平房仓中稻谷堆的沉降
依据式(7),以最底层的深度为纵坐标,储藏时间为横坐标绘出稻谷堆高的沉降曲线。
由式(3)与式(4)计算出不同储藏时间的稻谷堆最大主应力(竖直压应力)与密度,拟合稻谷堆压缩密度与储藏时间及最大主应力(竖直压应力)关系模型为:
3 结果与分析
3.1 稻谷堆压缩密度与储藏时间及最大压应力(竖直压应力)关系模型
将镇稻19号(含水率12.93%)储藏在6个装样筒中(顶部压应力分布为50、100、125、150、175、200 kPa),持续压缩4个月。
3.1.1 不同顶部压力和储藏时间下的稻谷堆密度
依据式(4)计算得到稻谷堆在不同顶部压力、不同储藏时间下的压缩密度,见表1。

表1 不同顶部压力、不同储藏时间下稻谷堆的压缩密度/kg/m3
由表1可知,随着储藏时间的增加和顶部压力的增加,稻谷堆的压缩密度逐渐增加。
3.1.2 不同顶部压力和储藏时间下稻谷堆受到的最大压应力(竖直压应力)
由式(3)计算出稻谷堆(镇稻19号)在不同顶部应力、不同储藏时间的最大压应力(竖直压应力),见表2。

表2 不同顶部压力、不同储藏时间下稻谷堆所受到的竖直压应力/kPa
3.1.3 稻谷堆的压缩密度与储藏时间及最大压应力(竖直压应力)的关系模型
目前,国外East等[4]开发了辅助设计评审人员的工具(Reviewer助手)来协助审核人员。国内针对施工图审核的软件有:①理正施工图校对审核软件2.0版[5],该软件是针对“结构平法施工图进行校核”的专用软件,对施工图格式要求低且识别率高、能够快速定位配筋不满足要求的构件,但它仅针对梁配筋图进行审核;②武汉理工大学利用VB程序语言编程,开发了一类面向审图机构的审图工程师的建筑结构施工图审查软件[6-8]。该类软件主要针对常用基础类型、框架结构、剪力墙及框架——剪力墙结构施工图审查过程数字化,目前尚未正式投入使用。
由表1和表2中数据的特性,设稻谷堆压缩密度与储藏时间及最大压应力的关系模型为:
ρ=ρ0+(ρmax-ρ0)(1-eapv3+bpv2+cpv+d)
(8)
式中:ρ为稻谷堆压缩密度, kg/m3;ρ0为稻谷堆所最小受压应力密度(顶部压力为50 kPa), kg/m3;ρmax为稻谷堆所受最大压应力密度(顶部压力为200 kPa), kg/m3;ρv为稻谷堆受到的最大主应力(竖直压应力), kPa。其中,ρ0=ρ0(T),ρmax=ρmax(T)。
3.1.3.1 稻谷堆的压缩密度与储藏时间的关系
ρ0=562.87+1.606ln(T)
依据表1中的数据,顶部压力为50 kPa时稻谷堆的压缩密度与储藏时间ln(T)关系曲线的拟合方程为:
(9)
依据表1中的数据,顶部压力为200 kPa时稻谷堆的压缩密度与储藏时间ln(T)的关系曲线的拟合方程为:
ρmax=608.94+2.711ln(T)
(10)
3.1.3.2 稻谷堆的压缩密度与储藏时间、最大压应力(竖直压应力)之间的关系
将式(8)两边同时取对数将其变换成式(11)为:
(11)
依据表1和表2中的数据,以ln[1-(ρ-ρ0)/(ρmax-ρ0)]为纵坐标、pv为横坐标作曲线图,由曲线图拟合方程得出:a=-0.000 001,b=0.000 2,c=-0.013 5,d=0.000 3。
将a,b,c,d的值及式(9)、式(10)代入式(8),可得推导稻谷堆压缩密度与储藏时间及最大压应力(竖直压应力)的关系式为:

(12)
3.1.3.3 模型的验证
标准化的目的是“为了在既定范围内获得最佳秩序,促进共同效益”,比如全国正在推行的科学有效的政务大厅服务标准,目的就是为了简化办事程序、提升服务效能,方便老百姓,使社会管理和公共服务获得最佳秩序和共同效益。为使产品、过程或服务适合其用途,标准化活动可以有一个或多个目的,且这些目的可能相互重叠。

图2 稻谷堆压缩密度随储藏时间变化的测量值与模拟值对比
由图2可知,稻谷堆压缩密度的模型预测值(虚线)与实验测定值之间的相对误差低于0.07%,RMSE的值在0.348 3~1.798 8 kg/m3之间,误差较小,所以该模型可以用于计算稻谷堆随储藏时间与竖直压应力变化的密度值。
3.2 平房仓中各稻谷层的平均竖直压应力
选定平房仓内稻谷堆长26 m、宽24 m、高9 m(重力未施加,粮堆无压缩状态)。
将平房仓中的稻谷堆平均地分为9层,每层的厚度为1米(重力未施加)。使用有限元软件ABAQUS求解稻谷堆修正剑桥模型计算出平房仓中稻谷堆的竖直压应的力三维分布值。由稻谷堆的竖直压应力的三维分布值计算出各稻谷层的平均竖直压应力如表3中的第2列数据所示。
2018年秋天,一批有才华有情怀的文友在订户相对集中的市县牵头设立了五十多个《星火》读者驿站,把星火燎原的祝愿变成了隐约可见的现实。

表3 平房仓中不同储藏时间不同粮层下稻谷堆粮层密度/kg/m3
3.3 平房仓中稻谷堆密度与粮层深度及储藏时间关系
依据各稻谷层的竖直压应力值(表3中的第2列数据),由式(12)计算出平房仓中稻谷堆不同储藏时间的各粮层的平均密度,见表3。
依据表3中各稻谷层的密度值和质量计算出不同储藏时间各稻谷层的深度值,见表4。

表4 平房仓中不同储藏时间下不同粮层下稻谷堆的粮堆深度/m
由表3、表4中的数据特性,设平房仓内稻谷堆压缩密度与储藏时间及粮层深度的关系模型为:
学生动手操作后,师生一道总结得到判定方法2:两角及其夹边分别相等的两个三角形全等(简写为:“角边角”或“ASA”).判定方法3:两角分别相等且其中一组等角的对边也相等的两个三角形全等.(简写为“角角边”或“AAS”)
ρ=ρ0+(ρmax-ρ0)(1-eah3+bh2+ch+d)
(13)
式中:ρ为稻谷堆密度/kg/m3;ρ0为稻谷堆表层密度/kg/m3;ρmax稻谷堆底层密度/kg/m3;h为稻谷堆粮层深度/m。
依据表3中的数据,平房仓中稻谷堆的表层密度与储藏时间ln(T)拟合线性方程为:
ρ0=566.94+1.678ln(T)
(14)
式中:T为平房仓中稻谷堆的储藏时间/月。
依据表3中的数据,平房仓中稻谷堆底层与储藏时间ln(T)拟合线性方程为:
ρmax=578+1.908ln(T)
(15)
将式(13)转化为式(16)为:
(16)
依据表3、表4中的数据,以ln[1-(ρ-ρ0)/(ρmax-ρ0)]为纵坐标、h为横坐标作曲线图,拟合线性方程得到a,b,c,d的值分别是-0.011 8, 0.108 5,-0.678 2, 0.687 5。
将a,b,c,d的值和式(14)、式(15)代入式(13),可得稻谷堆密度ρ与储藏时间T及粮层深度h的关系模型为:
ρ=566.94+1.678ln(T)+(11.06+0.129ln(T)(1-e-0.011 8h3+0.108 5h2-0.687 2h++0.687 5))
(17)
由式(17)计算的预测值与实验测定值见图3。
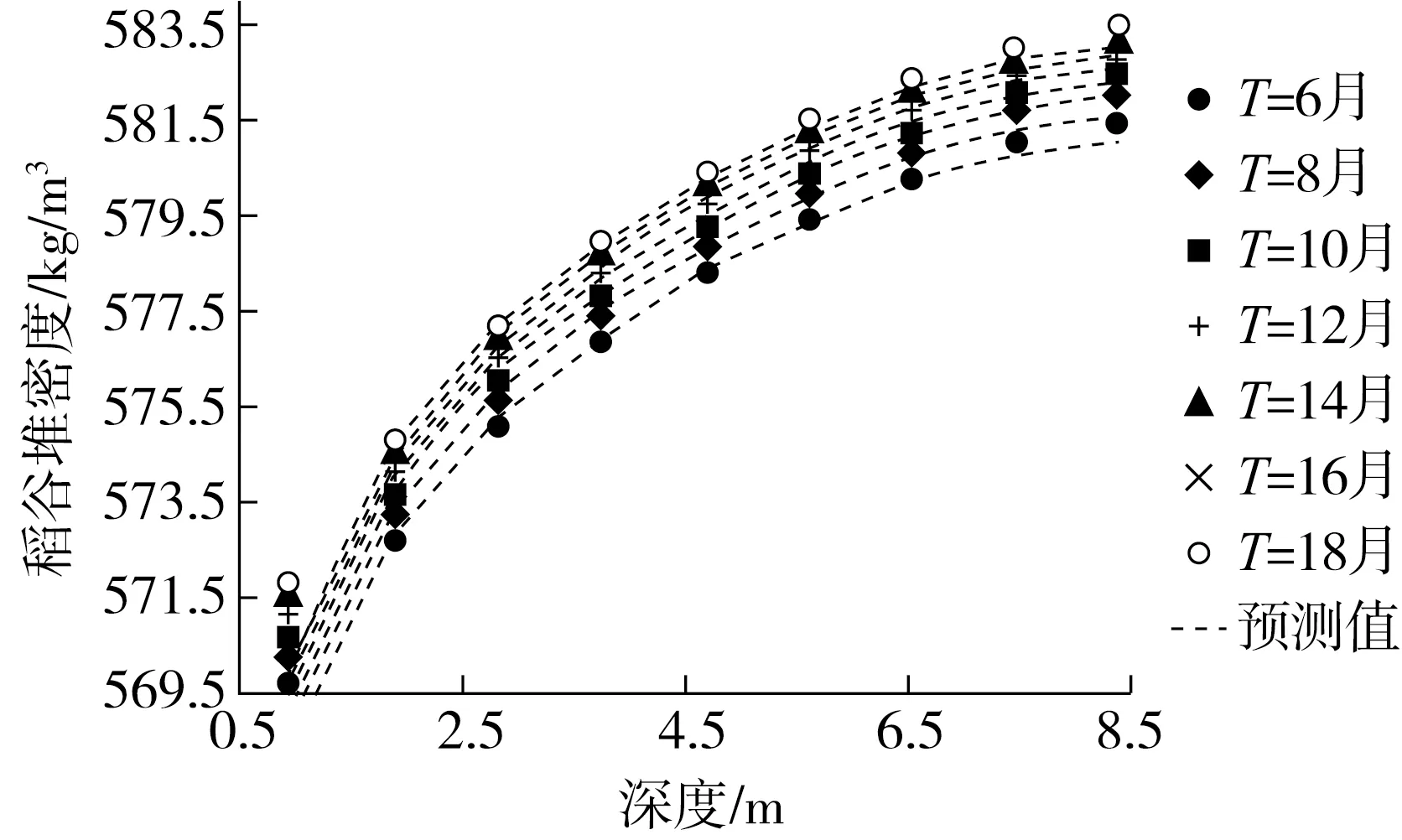
图3 稻谷堆压缩密度随储藏时间、粮层深度变化的实验值与预测值对比
从图3可见,经式(17)计算得到的稻谷平均粮层密度(预测值)与试验测定的密度对比发现,两者相对误差小于0.05%,其RMSE的值在0.181 5~0.934 2 kg/m3之间, 误差较小,则该模型可以用来预测平房仓中稻谷堆不同储藏时间、不同粮层深度下的粮层密度。
3.4 平房仓中稻谷堆高的沉降
平房仓中最底层的深度等于堆高。依据表4,以最底层的深度为纵坐标,储藏时间为横坐标绘出稻谷堆高的沉降曲线如图4所示。

图4 稻谷堆粮堆高度随储藏时间的变化关系
由图4可知,随着储藏时间增加,稻谷堆高逐渐减小,但堆高减小幅度越来越小,沉降曲线最终趋于平缓。稻谷堆储藏在平房仓中,在储藏初期稻谷堆内的孔隙率较大。随着储藏时间的增加,稻谷堆持续受到压应力作用,稻谷堆持续被压缩,导致其孔隙率越来越小,稻谷堆越压越实,其体积逐渐减小直至趋于恒定,从而导致堆高度减小幅度越来越小直至高度趋于恒定值。
4 结论
稻谷堆的压缩密度随最大主应力的增加而增大,随储藏时间的增加而增大。稻谷堆密度关于储藏时间和最大主应力的关系模型为:

平房仓中稻谷层密度随粮层深度的增加而增大,随储藏时间的增加而增大。平房仓中稻谷层密度关于储藏时间和粮层深度的关系模型为:
ρ=566.94+1.678ln(T)+(11.06+0.129ln(T)(1-e-0.011 8h3+0.108 5h2-0.687 2h++0.687 5))。
平房仓中稻谷堆高随储藏时间的增加而降低,且堆高降低幅度越来越小,最后堆高趋于稳定值。

