基于并行学习鲁棒自适应的行驶车辆特性参数估计方法研究

汪月英 梁 峰

1(长春汽车工业高等专科学校 吉林 长春 130013) 2(第一汽车集团公司教育培训中心 吉林 长春 130013) 3(长春职业技术学院 吉林 长春 130000)

0 引 言

车辆作为现代社会的主要交通工具之一，造就了全民用车的时代。正是这样广泛的市场和人民生活需求驱动了业界和各个科研机构对车辆系统开展了深入系统的研究[1-5]。现有多数研究致力于提升驾驶体验，工程师们设计了车辆电子稳定控制系统(ESC)、电子稳定程序(ESP)、主动转向系统(AFS/ARS)、主动车身控制(ABC)等[2-3]。

为提升驾驶体验，增强车辆对环境的适应性，要求车辆控制系统具有精准的控制能力，而此类控制器依赖于车辆本体参数、道路参数、环境参数[3]。准确而实时地获取车辆行驶过程中的状态信息是车辆电子控制系统研究的关键，可为车载故障诊断系统的实时监控和预警提供快速准确的信息，是实现精准闭环控制的前提和必要条件[4-5]。在实际研究过程中，直接测量车辆侧偏角、路面附着系数、轮胎侧偏刚度这些状态或参数是非常困难的，成本也非常高。因此，用传感器测出易获取的变量，再进行状态参数估计，是一种非常重要的辅助测量手段[6]。

针对行驶车辆的特性参数估计问题，业界和学者们开展了广泛的研究。现有的方法主要有递推最小二乘方法(RLS)[7]、串行RLS算法[8]、嵌套RLS算法[9]、多遗忘因子RLS估计方法[10]等。除此之外，还有扩展卡尔曼滤波(EKF)、容积卡尔曼滤波算法(CKF)、强跟踪中心差分卡尔曼滤波器(CDKF)等[11-12]。特别是智能估计方法、观测器方法、最优化估计方法等，在汽车操纵稳定性和主动安全控制方面得到了广泛应用。在上述方法中，参数估计方法因其解耦合、高灵活、强适应等特点得到了较好的推广和应用[4,13]。

上述未知参数估计方法存在两个主要问题：(1) 参数估计不够直接；上述方法通常需要两步实现问题求解。第一步，对系统状态进行估计；第二步，根据状态估计误差设计参数更新律。其实质是状态跟踪误差来驱动未知参数估计的收敛。这种方式虽然有效，但由于系统状态估计本身存在误差，该误差传递给参数估计律进一步增大了参数估计的误差，一定程度上使得参数估计律执行效率降低。(2) 需要持续激励信号以保证估计结果的收敛，而实际应用中保持持续激励信号较为困难[14]。

本文通过构建参数估计的直接误差信息直接驱动参数估计的收敛，提升参数估计效能。与此同时，结合并行学习技术放宽参数更新的持续激励条件，以期进一步提升方法的工程应用效率，为工程实践提供一定参考。

1 问题描述

考虑含外部扰动的行驶车辆，见图1(注：① 为重力第一分量;② 为空气阻力;③ 为汽车重力与地面作用产生的摩擦力;④ 为路面粘性摩擦力)。其纵向运动方程如下[15-16]：

(1)

式中：m为车辆质量；V为车辆纵向行驶速度；F为车辆动力；g为当地重力加速度(取值9.8 m/s2)；θ为路面坡度；Cvf为粘性摩擦系数；Cu为轮胎滚动摩擦系数；C为空气阻力系数；d为外部扰动。

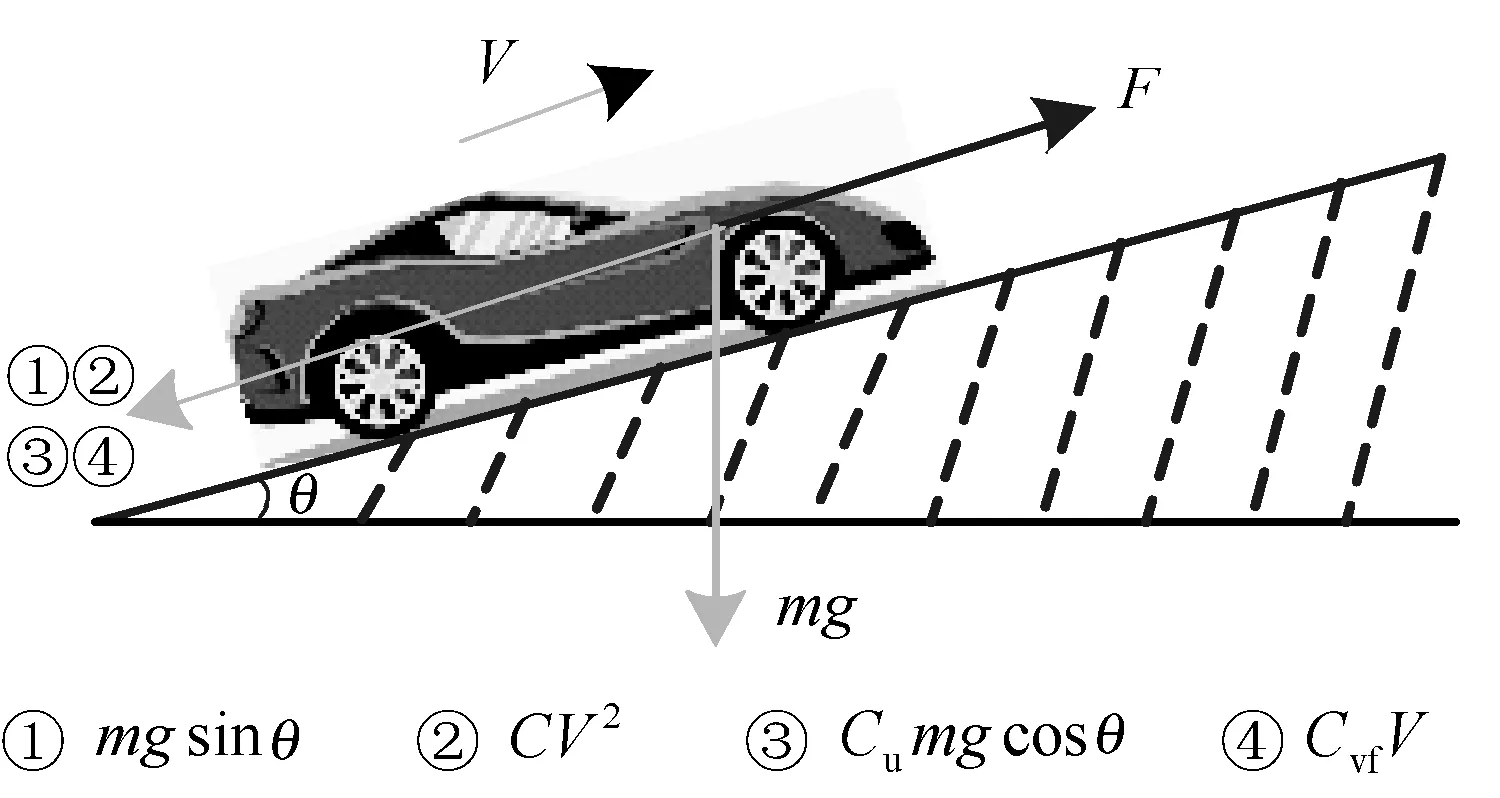
图1 行驶中车辆的受力分析

假设1鉴于能量有限，假设因传感器噪声等引起的外部扰动d是有界的，即：

d≤d*

(2)

式中：d*为未知常数。

假设1是一般假设，具有一定合理性。

为便于进行参数估计方法设计，对式(1)进行未知参数仿射变换，得到：

G(F,V)β+d

(3)

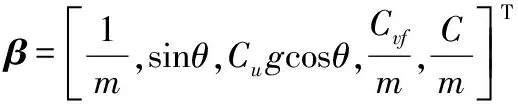
至此，本文所研究的车辆行驶特性参数估计问题转换为仿射参数估计问题。针对该问题，本文将从低通滤波去噪、直接参数估计误差构建、鲁棒自适应参数估计律设计及其稳定性/鲁棒性分析进行详细阐述。

2 鲁棒自适应参数估计律设计

2.1 低通滤波去噪

低通滤波器具有良好的去噪性能，在光纤陀螺、电机向量控制和信号处理等抗干扰方面得到了广泛的应用[17-19]。鉴于此，本文采用低通滤波思想，引入下列车辆状态变量及响应函数的一阶滤波变量：

(4)

式中：κ>0是待设计的滤波器参数；Vf、Gf和df分别是对应变量的一阶滤波变量；df仅用于稳定性证明，无须准确计算。

根据式(3)和式(4)可得：

(5)

根据式(4)中的滤波变量，采用并行学习技术[20]，以放宽自适应参数估计收敛的持续激励条件，具体参数估计律设计详述如下。

2.2 直接参数估计误差构建

定义辅助回归矩阵Wcl(t)和辅助向量Fcl(t)为：

(6)

式中：l>0为待设计参数；Wcl(t)和Fcl(t)是经并行学习得到的回归矩阵和向量表达式；Ws和Fs为对应历史回归矩阵和向量；Gf(ti)、V(ti)和Vf(ti)为时刻ti处并行学习所记录的数据点；q为记录数据的内存容量，根据设备内存和算法实现效果进行优化选取。在上述辅助变量中引入了辅助回归矩阵/向量的历史数据，其作用在后续内容中进行详尽说明。由式(6)可知：

(7)

根据回归向量定义式(6)，可得考虑扰动的估计误差为：

(8)

式中:‖ξ(t)‖≤ξ*，ξ*∈R+，且有：

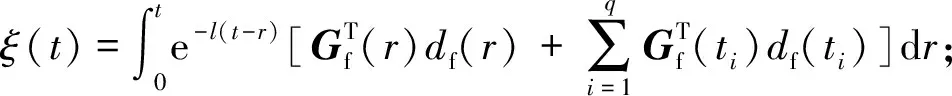
2.3 参数估计律设计

根据梯度下降规则，可设计故障估计器为：

(9)

式中：Γ=ΓT>0是待设计参数之一，表征参数估计的更新速率。对比式(8)和式(9)可见，上述参数估计律直接由参数估计误差直接驱动故障估计过程，这与常规状态跟踪误差驱动的间接方式截然不同，突出了本文方法的优势所在。

3 稳定性分析

为保证所设计参数估计律能够有效估计行驶车辆的未知参数，利用以下定理对其稳定性和鲁棒性进行分析。

定理1对于含外部扰动的行驶车辆式(1)，在满足假设1的情况下，所设计参数估计律式(9)可保证估计误差的全局一致最终有界。

证明：选取Lyapunov函数为：

(10)

L的正定性得以保证。在考虑扰动的估计误差式(8)条件下，对L沿参数估计律式(9)求取时间t的导数可得：

(11)

需要注意的是，根据文献[21]，需回归矩阵Wcl(t)满足持续激励条件，上述参数更新律方可自适应收敛，而业界通常保证持续激励的方式是向系统输入信号中加载一定规则的扰动信号，从而保证参数更新律的收敛。而在参数估计收敛之后，又需要将其有效移除，这无疑给工业应用带来了诸多不便。本文合理利用并行学习技术[20]，能够有效解决上述问题，放宽了持续激励条件。同时，本文中的历史数据采用最小特征值最大化算法[22]进行筛选，通过设置最大数据量q节省了硬件平台内存，并保证了回归矩阵更新的高效性。

为了解本文方法全貌，现给出详细方法步骤如表1所示。

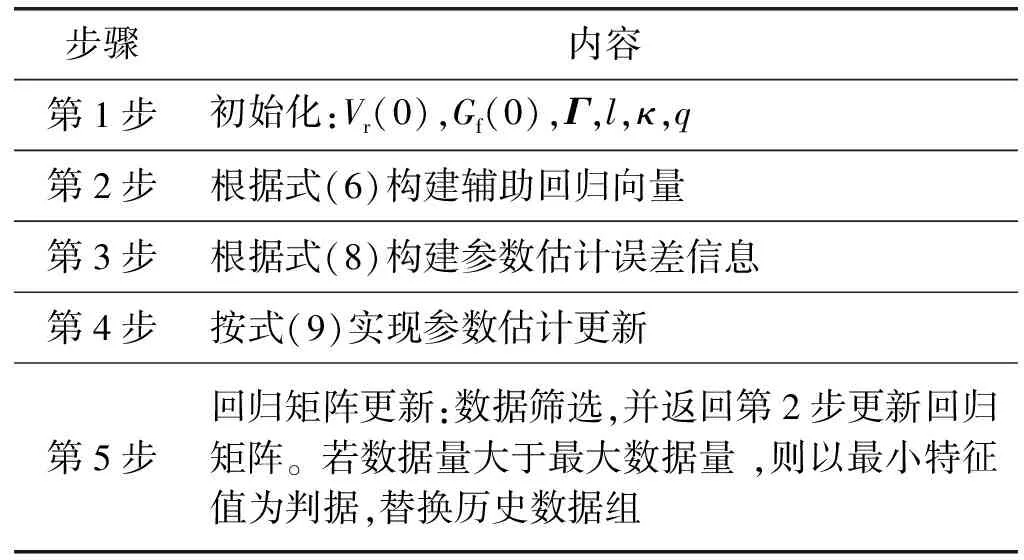
表1 设计方法步骤

4 仿真分析

为验证本文方法的有效性，在配置内存8 GB、装有64位Windows 10操作系统的PC机上，以MATLAB2018b为仿真软件对本文方法进行验证。引入某型号车辆的参数。详见表2。

表2 车辆行驶参数

给定参数更新律的相关设计值：Γ=10I5，I5为5阶单位矩阵，l=1，κ=0.001，q=10。为说明本文方法在非持续激励条件下的仿真效果，车辆动力F选取为阶跃信号(阶跃信号为一种非持续激励信号)[23]。

以回归最小二乘方法(RLS)为对比，详细阐述本文方法的优越性。不考虑外部有界扰动时的参数更新如图2所示。

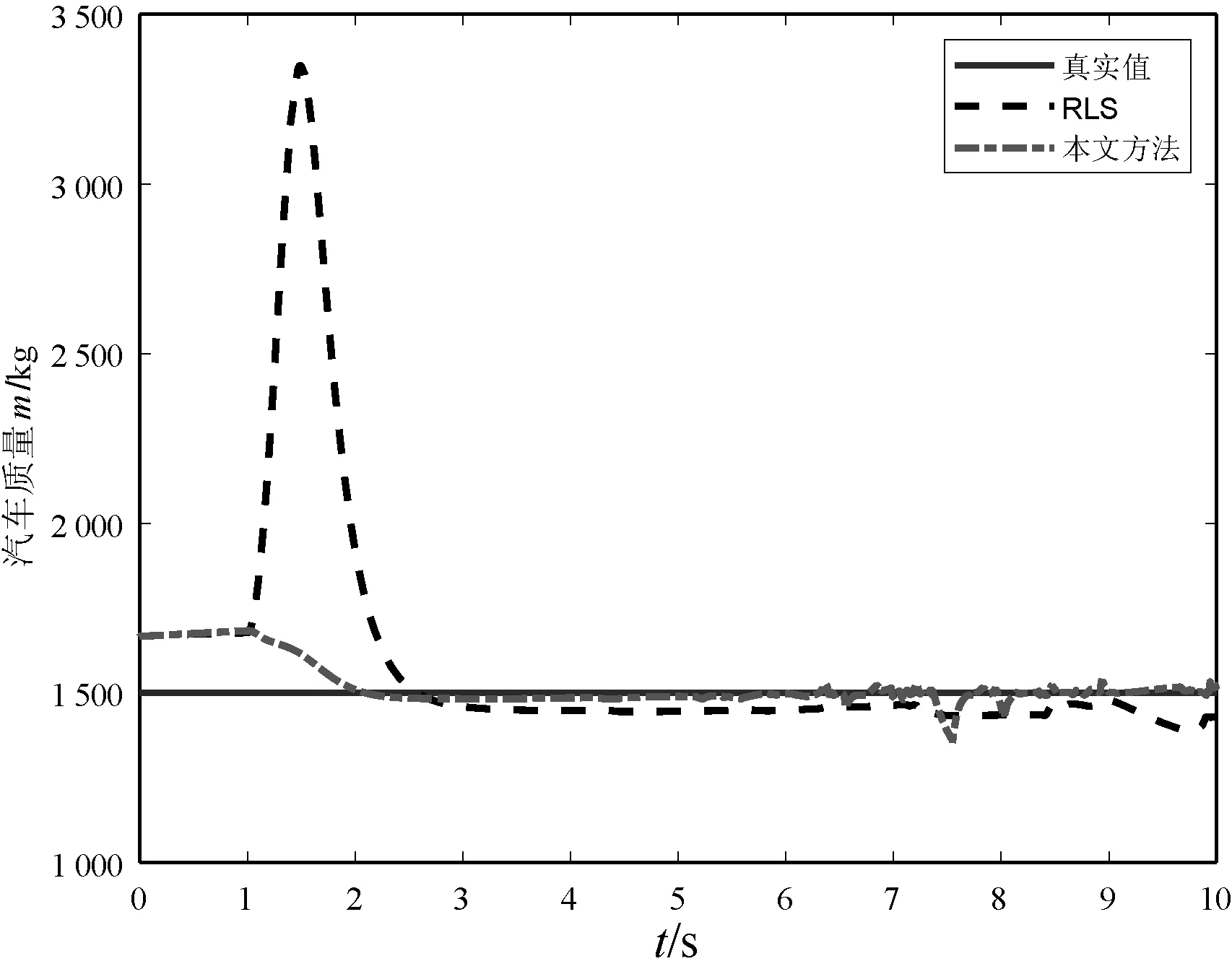
图2 质量m估计

观察图2可知，较之RLS方法，本文方法能够较快地收敛到真实值且参数估计超调量较小，具有较好的参数估计性能。从参数最终收敛效果可以看出，因为激励信号的非持续激励特性，RLS方法无法保证收敛到真实值，仅收敛到真实值的邻域内，所以存在一定静态误差。而本文方法能够较好收敛到真实值，参数估计效果好。

观察图3可知，RLS方法与本文方法在估计Cvf系数的过程中均有两次较大波动，但本文方法估计曲线的波峰与波谷明显超前于RLS方法，说明本文方法收敛速度较快。

图3 Cvf的估计

观察图4可知，对于较小参数(Cu=0.01)的估计，本文方法亦能实现较好估计，误差小，能够满足现实需要。

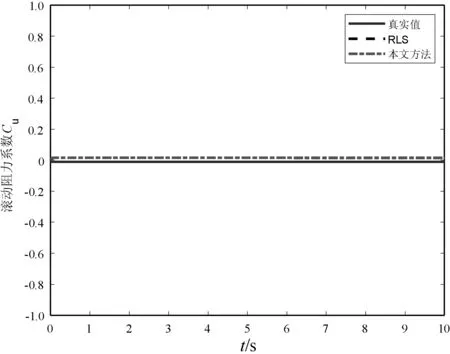
图4 Cu的估计

图5与图3具有类似的参数估计收敛效果，充分说明了本文方法能实现各特性参数的较好估计，有效提升了估计方法的快速性，提高了估计效率。

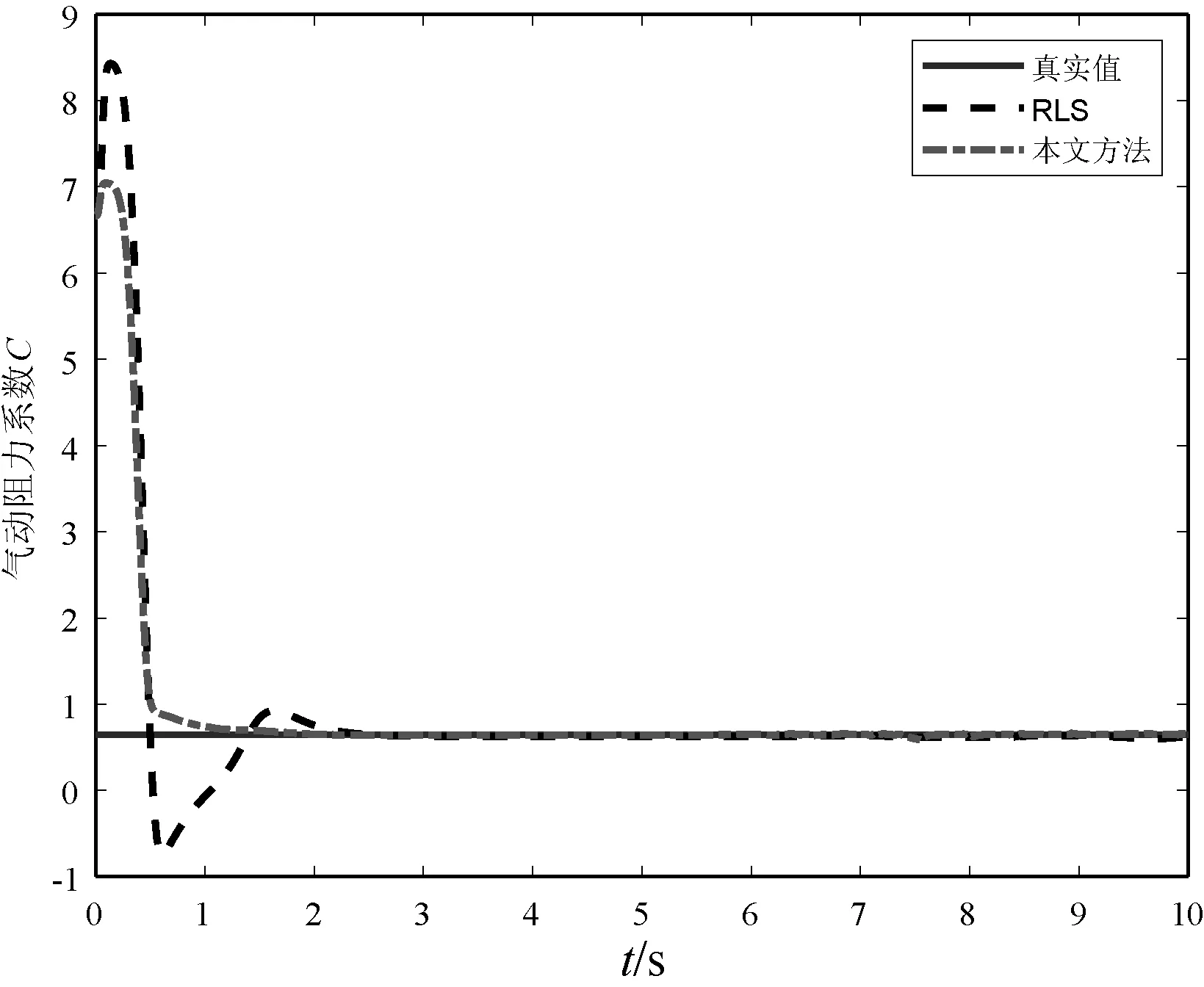
图5 C的估计

进一步观察数据点个数(图6)可知，本文方法能够如此高效地得到接近真实值的估计值是因为本文所采用并行学习技术中的数据筛选算法得到了有效发挥，满足条件的历史数据很快就达到了最大数据量，但随着仿真时间推移，数据组的内容有部分调整，使得参数更新更优。

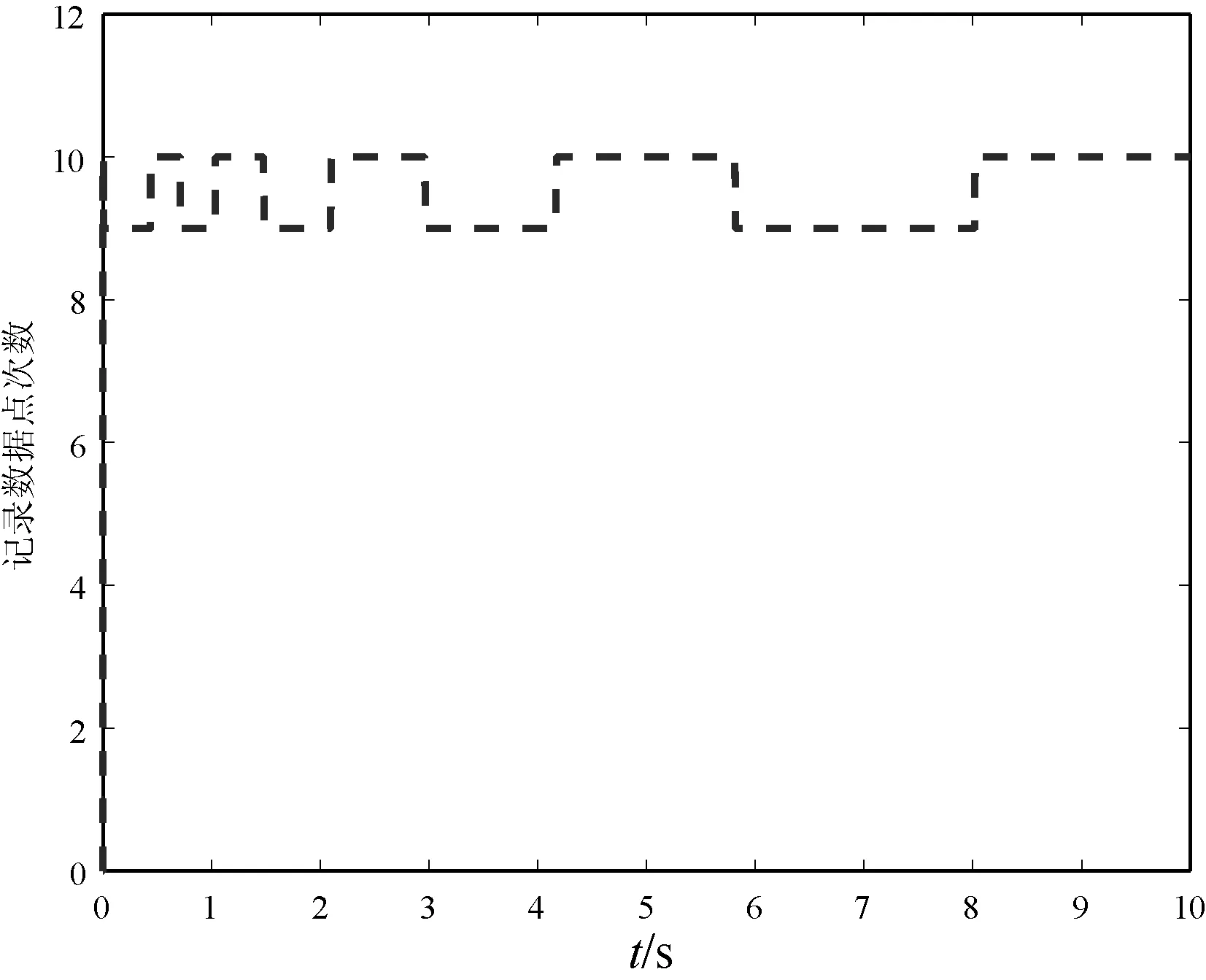
图6 记录的数据点个数(q)

为验证本文方法的鲁棒性，在系统状态方程中考虑了如下扰动：d1=0.1sin(50t)，d2=sin(20t)，d3=0.05sin(100t)，d4=d5=0。其他参数与无扰动情形保持一致，仿真结果如图7-图10所示。

图7 含扰动的质量m估计

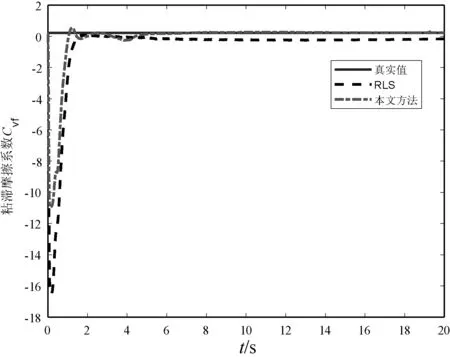
图8 含扰动的Cvf估计

图9 含扰动的Cu估计

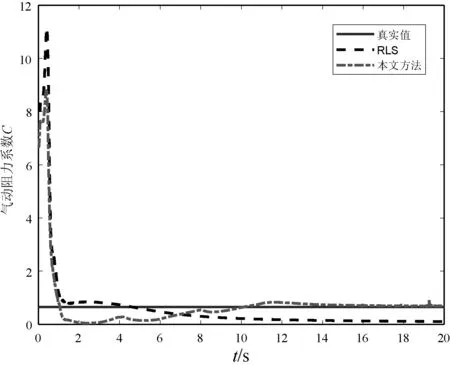
图10 含扰动的C估计

观察图7可知，扰动情形下，一方面，本文方法的收敛优势更为明显，能够保证参数的高效收敛。实际应用中对汽车控制系统输入持续激励信号进行故障诊断费时费力，而本文方法正好解决了非持续激励条件下的汽车行驶参数估计问题。另一方面，从收敛过程来看，两种方法的参数估计结果变化较大，相比而言，本文方法波动更多。因为本文方法所设计参数更新律是参数估计误差直接驱动，驱动力较大，收敛速度较快，但鲁棒性较弱，这也印证了快速性与鲁棒性是一对矛盾体的自然认知。从收敛结果来看，RLS方法已然出现发散趋势，但本文方法仍能收敛到真实值的邻域内。图8中的仿真结果说明本文方法对于小幅值参数的估计具有良好的鲁棒性。即使存在扰动，也能保证较好的收敛结果。图9和图10中，RLS方法仅能保证收敛到真实值的邻域内，而本文方法仍具有较好的收敛性能，这充分说明了本文方法的优越性。

分别对比图4与图9、图5与图10可知，本文方法对于小幅值特性参数的估计具有快速性和强鲁棒性兼容的优良性能。对比图2和图7可知，本文方法对于大幅值特性参数的估计具有快速性，但鲁棒性相对小幅值参数估计较弱，有待进一步提高。

通过上述仿真结果分析可知，本文方法能够实现行驶车辆特性参数的有效估计，兼顾直接性、鲁棒性和快速性且放宽了持续激励条件，提升了故障诊断单元工作效能，能够为汽车安全控制系统提供精准的车体和路况信息，保证控制系统良好运行，保障人车安全。

5 结 语

本文针对车辆行驶过程中的特性参数估计问题，结合并行学习技术，提出一种鲁棒自适应故障估计方法，并通过仿真验证得到以下结论：

(1) 本文方法能够实现车辆行驶特性参数及时有效地估计，估计时间短(除车辆质量受扰较大之外，其他参数均可在3 s内实现有效估计)。

(2) 本文方法对外部有界扰动具有良好鲁棒性，能够实现大/小幅值(质量/环境系数)含扰动情形下的有效估计，与传统RLS方法相比具有收敛速度快、误差小的特点，为工程实践提供一定参考。