考虑轨道约束的连续梁拱桥地震反应及减震控制研究

石 岩，赵翔宇，焦应乾，刘云帅，张胶玲

（兰州理工大学土木工程学院，甘肃兰州 730050）

引言

连续梁拱组合桥因其横向刚度大、跨越能力强以及造型优美而广泛应用于铁路桥梁中［1－3］。近年来，国内学者围绕其动力响应问题开展了一些研究。黄艳等［4］采用非线性弹簧单元模拟道床的纵向位移阻力关系，建立了桥梁与轨道一体化模型，分析了桥墩刚度相近和相差较大时道床阻力对桥梁的地震反应；谢旭等［5］发现随着道床阻力系数增大，桥梁纵向自振频率也随之增大，且当道床阻力系数超过10 kN/m 时，道床阻力系数增加对结构自振频率及地震响应影响较小；戴公连等［6］对比了温度、活载和混凝土收缩徐变等作用下连续梁桥与梁拱组合桥上无缝线路纵向力的分布规律；刘正楠等［7］分析了行波效应对有轨道约束和无轨道约束两种体系桥梁地震响应的影响。已有研究表明轨道约束可以降低桥梁的地震响应，但钢轨应力又与桥墩刚度有关，轨道约束不可忽略［5，8］。可见，既有研究关注轨道约束效应对地震响应的影响较多，对连续梁拱桥与连续梁桥的差异及拱肋的影响等问题涉及较少。

目前，减隔震装置在建筑和公路桥梁中应用广泛，而铁路桥梁需要保证行车安全和稳定性，使其应用减隔震技术时需更加谨慎。另外，铁路震后的首要任务是在尽短的时间内恢复通车，这要求桥梁要满足地震损伤可控及具备被快速修复条件［9］。因此，功能分离理念在铁路桥梁减隔震设计中得到较多关注，温留汉·黑沙等［10］提出了摩擦支座提供竖向支撑，铅芯橡胶支座提供横向约束的减震系统，并通过振动台试验验证了减震系统的有效性；李爱丽等［11］提出了“活动盆式支座-减震榫”的高速铁路桥梁减震系统，通过数值分析和试验研究表明可以取得较好的减震效果；石岩等［12，23］对“活动盆式支座-耗能支撑”和“活动盆式支座-减震榫-拉索限位器”两种减震体系在近断层地震动下的性能进行研究。以上研究提出了一些铁路桥梁的组合减隔震装置并验证了其有效性，但均未考虑轨道约束对减隔震桥梁抗震性能的影响。

本文以一座连续梁拱桥为研究对象，通过非线性动力时程分析，研究了轨道约束和拱肋对连续梁拱桥地震位移响应的影响，比较了“减震榫-拉索限位器”与“SCEDB-BRB”两种减震控制系统的减震效果，最后对耗能支撑的布置角度进行了优化设计。

1 工程概况及分析模型

1.1 工程概况

以一座跨径为（62+132+62）m 的铁路连续梁拱桥为研究对象，其主梁采用单箱单室预应力混凝土连续梁，拱肋采用哑铃型截面的钢管混凝土，拱轴线为二次抛物线，跨中截面高3.5 m，其拱肋设计矢高为22 m，矢跨比为1/6。桥墩为双流线型圆端实体墩，净高9 m，全桥设14 对吊杆，吊杆沿顺桥向间距8 m。0#和3#台设置有纵向和多向活动的球形钢支座GTQZ-Ⅲ-3 500 ZX（DX），1#墩顶安装有纵向和多向的球形钢支座GTQZ-Ⅲ-45 000 ZX（DX），2#墩顶安装有横向和固定的球形钢支座GTQZ-Ⅲ-45 000 HX（GD）。梁拱组合桥布置图如图1所示。

图1 大跨度铁路连续梁桥Fig.1 Long-span railway continuous beam-arch bridge

1.2 分析模型

基于OpenSees 地震分析平台建立连续梁拱桥的动力分析模型，如图2 所示。主梁、拱肋、吊杆以及钢轨用弹性梁柱单元模拟，桥墩采用纤维截面的非线性梁柱单元模拟，其中混凝土为Concrete01 材料本构，其单轴应力-应变关系采用Kent-Scott-Park 的混凝土模型，钢筋采用Steel02 材料，其应力-应变关系基于Giuffre-Menegotto-Pinto 模型；线路阻力选用双线性本构模型Steel01；滑动支座选用FlatSliderBearing 单元模拟；1#和2#桥墩上为钢挡块，采用Steel01 本构模型；桥台处为钢筋混凝土挡块，其应力-应变关系采用Hysteretic Material模拟，挡块与主梁的碰撞均采用ImpactMaterial本构模型。墩底固结，不考虑桩土相互作用。

图2 有限元模型图Fig.2 Finite-element model of prototype bridge

为了讨论轨道约束效应、拱肋对连续梁拱桥动力特性和地震反应的影响，以及不同类型减震控制系统的性能，本文共采用了6 种分析模型，其基本特征见表1。其中：除模型A 外，其他模型都考虑了轨道约束效应，6种分析模型的上部结构总质量均相等。

表1 分析模型特征Table 1 Characteristics of analysis models

（1）轨道约束效应

桥梁和钢轨之间连接单元的模拟是分析梁轨相互作用的关键，模拟方式主要为非线性弹簧单元、抗弯杆件以及桁式杆件等［13－15］，其中：非线性弹簧来模拟纵向阻力的传力规律已经得到了国内众多学者的认同。轨道边界的约束条件是解决桥梁与路堤连接问题的关键，文献［5］提出当路堤上轨道长度为200 m及以上时对结构的地震响应影响较小，因此本文取200 m为路堤上轨道长度，并把此长度内弹簧简化为单一弹簧来模拟桥梁与路堤的连接。FRYBA［16］最早提出描述纵向阻力的弹簧模型，其位移-阻力关系如图3（a）所示。连接弹簧的刚度由纵向阻力推导得出，假设弹簧刚度为k0c；弹簧间距为l0；梁轨相对位移为μ；纵向阻力为r；一个等效弹簧的纵向阻力总和为：

非线性弹簧提供的纵向阻力总和为：

由Fyc=得弹簧纵向刚度k0c：

在无上部荷载作用时小阻力扣件线路阻力根据《铁路无缝线路设计规范》的规定取Fyc为15 kN/m，屈服位移为2 mm。由式（3）可得梁轨相对位移小于等于屈服位移时弹簧刚度取7 500 kN/m，当μ大于2 mm 时，kc=0。

（2）耗能支撑和支座

为了控制连续梁拱桥的地震反应，采用BRB 和SCEDB 作为水平耗能减震装置。BRB 芯材为钢材，截面为十字形，约束屈服段包在砂浆套筒中，SCEDB 核芯为形状记忆合金棒。SCEDB 自恢复耗能支撑的滞回模型呈旗帜型，其特点是在加载、卸载恢复至初始状态时，对应的残余位移为零，具有良好的自恢复性能，其恢复力曲线如图3（b）所示。在本构关系中，α 表示屈服后刚度和初始刚度的比值（αs表示SCEDB，αb表示BRB），β为耗能能力参数，反应了支撑耗能能力的大小，βFys定义为支撑的自恢复力，文中β取文献［17-18］中采用的0.95。BRB 本构采用经典的双线型滞回模型，如图3（c）所示。GTQZ 球形钢支座采用理想弹塑性模型模拟，其初始刚度按k0hb=μR/Dyhb计算，μ为滑动摩擦系数；R为支座所承担的上部结构重力；Dyhb为支座的屈服位移，如图3（d）所示。文中分析模型为宏观模型，主要体现单元整体力学特性对结构的影响，故不考虑构造细节对于单元力学特性的影响。单元力学参数见表2。

图3 恢复力曲线Fig.3 Restoring force curve

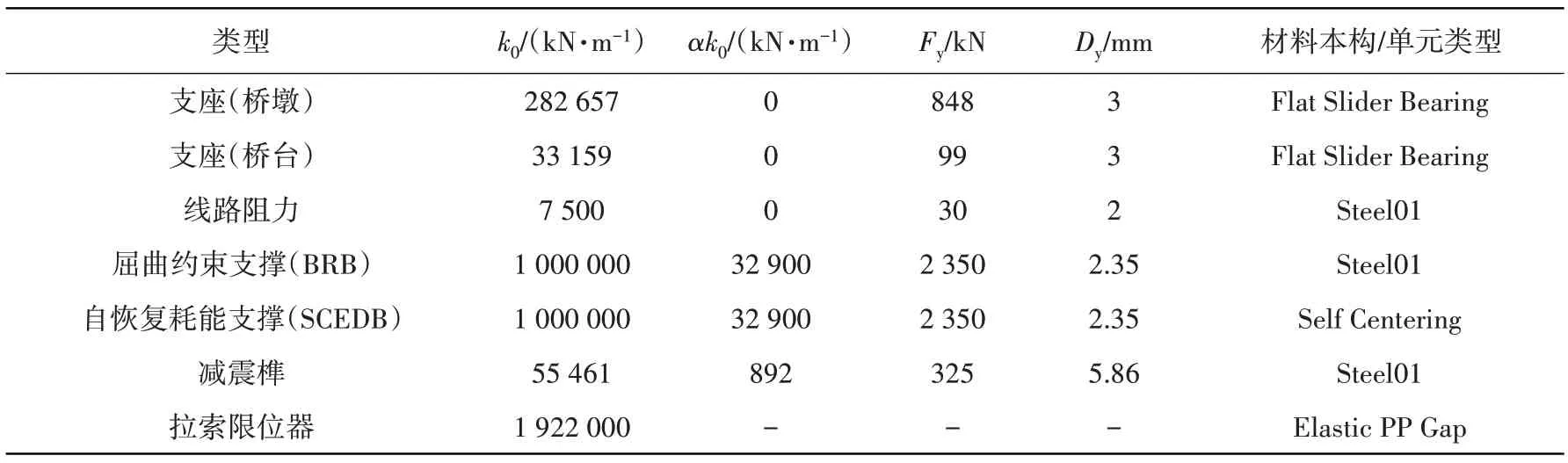
表2 单元力学特性参数Table 2 Mechanical feature parameters of element

1.3 地震动记录

BAKER 等［19］建立了广泛适用于交通领域结构动力分析的地震动记录集合，本文选取其地震动集合（SET#1B）中的40 组2 个水平分量的地震动记录。沿纵桥向输入垂直于断层的地震动分量（FN），沿横桥向输入平行于断层的地震动分量（FP），将FN 的PGA 调整为0.3 g（设计地震）；FP按FN 的调幅比例因子进行调幅后沿横桥向输入。

2 轨道约束的影响

铁路桥梁的轨道约束效应对减隔震装置的减震耗能作用可能起到限制作用。表3给出了考虑轨道约束效应（模型A和模型B）对连续梁拱桥自振周期和振型特征的影响，可以看出：轨道约束对结构纵向动力特性的影响较大，不考虑轨道约束模型（模型A）的第四阶振型为主梁沿纵桥向的刚体运动，而考虑轨道约束后该振型出现在第八阶，说明轨道约束给结构提供了一定的纵向刚度，使得结构沿纵桥向更不易发生振动。同时，轨道约束对结构横向变形的影响甚微，其原因在于轨道截面面积远小于主梁截面面积，其提供的横向刚度极其有限，可以忽略不计。

图4 为模型A 和模型B 在40 条双向地震动下主梁关键部位的峰值位移响应平均值，轨道约束对主梁沿横桥向的位移影响较小，而对主梁沿纵桥向的峰值位移有较大的约束作用，与表3 中动力特性的结果一致。可以认为，考虑轨道约束降低了上部结构纵桥向的地震反应，对限制桥梁上部结构纵向位移是有利的。但是，考虑到地震动的随机性、道床摩阻力的离散型、边界条件和减震装置工作原理差异等实际情况，为更准确地分析铁路桥梁的地震反应，非常有必要考虑轨道约束的影响。

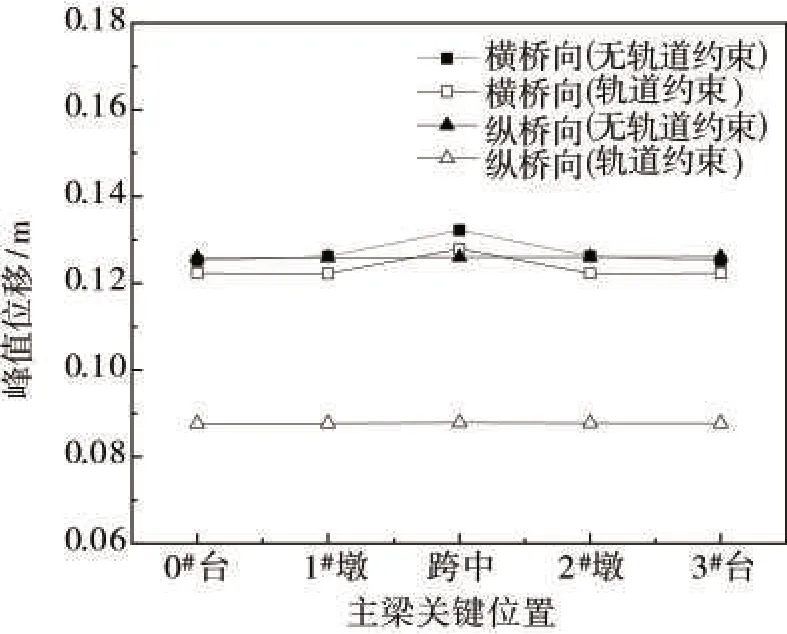
图4 主梁关键部位的峰值位移Fig.4 Peak displacement of key positions of girder

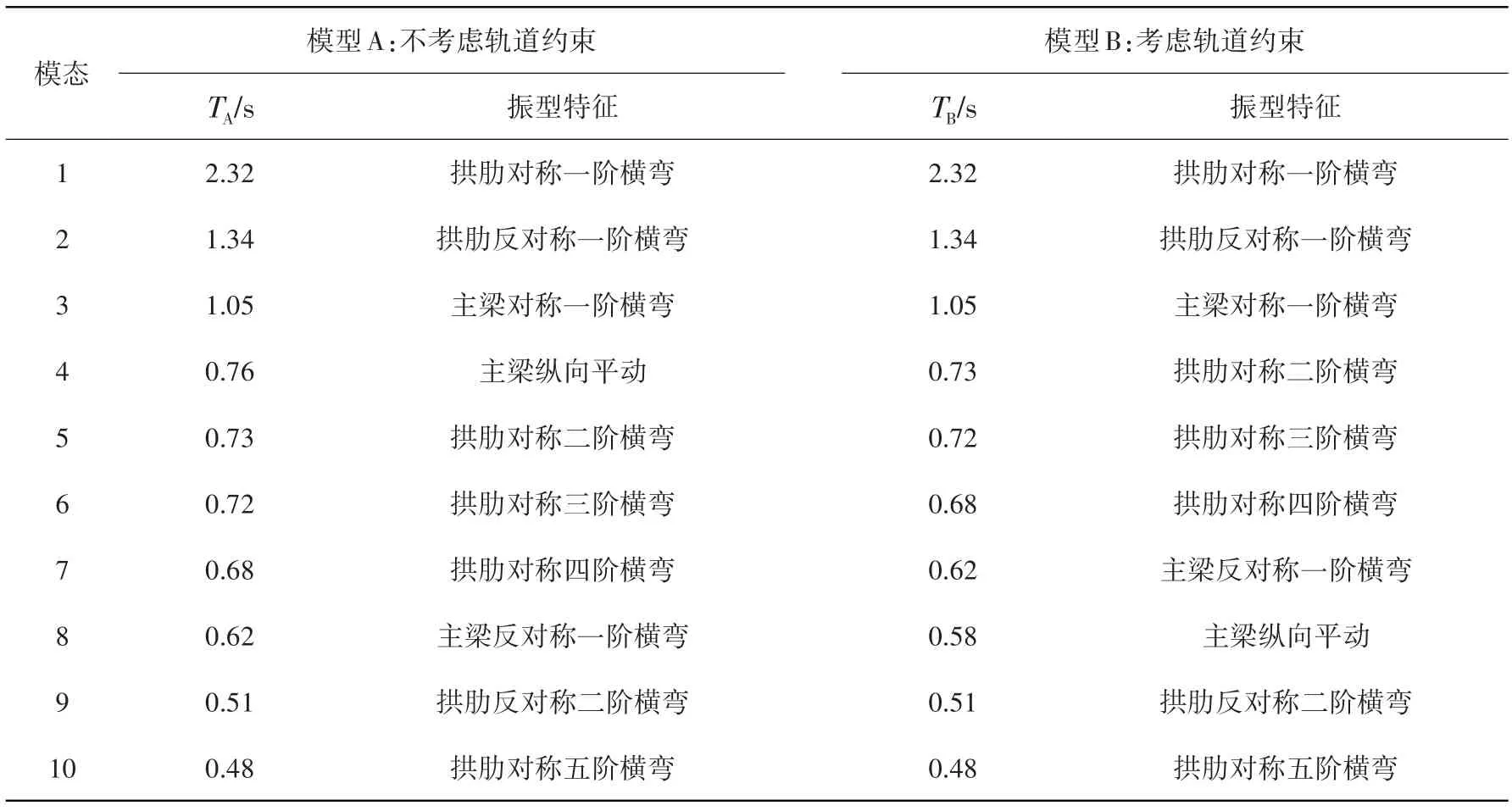
表3 轨道约束对自振特性的影响Table 3 Effect of track constraints on self-vibration characteristics

3 拱肋对横向地震反应的影响

连续梁拱结构是连续梁的中跨上架设拱肋的结构体系，拱肋对其竖向刚度和承载力提升较大，纵桥向与主梁整体性较好，但拱肋沿横桥向的刚度相对较小，容易发生横向变形，如表3 中的前两阶振型皆为拱肋的横向变形。梁拱组合结构作为一种复杂受力体系，拱肋与主梁的连接从施工到维护都增加了结构的安全风险［20］。汶川地震中黄江大桥和安州大桥在拱脚和主梁连接处均表现出较为严重的破坏，可见在横向地震作用下拱肋的存在对主梁地震反应可能存在不利影响。

为进一步探索拱肋对横向地震反应的影响，在考虑轨道约束（模型B）的情况下，假定桥台和桥墩处都设置滑动支座且没有侧向挡块，使得主梁能够自由运动；将拱肋质量分配给主梁，建立只考虑拱肋刚度贡献的连续梁拱桥模型（模型C）；模型D 为直接删除拱肋的连续梁桥，不考虑拱肋刚度，仅将拱肋的质量分配给主梁，使得3 种模型的上部结构总质量相等。表4 对比了模型C 和模型D 的前五阶周期和振型，二者的主要差异在于是否考虑拱肋的刚度，从两种模型的第一阶振型都为主梁的横向振动，周期相差不大，与模型B 的第三阶振型对应，说明两种模型的动力特性基本相同，拱肋对整个结构的横向刚度贡献较小，而拱肋自身的动力特性对该类结构的影响较大。

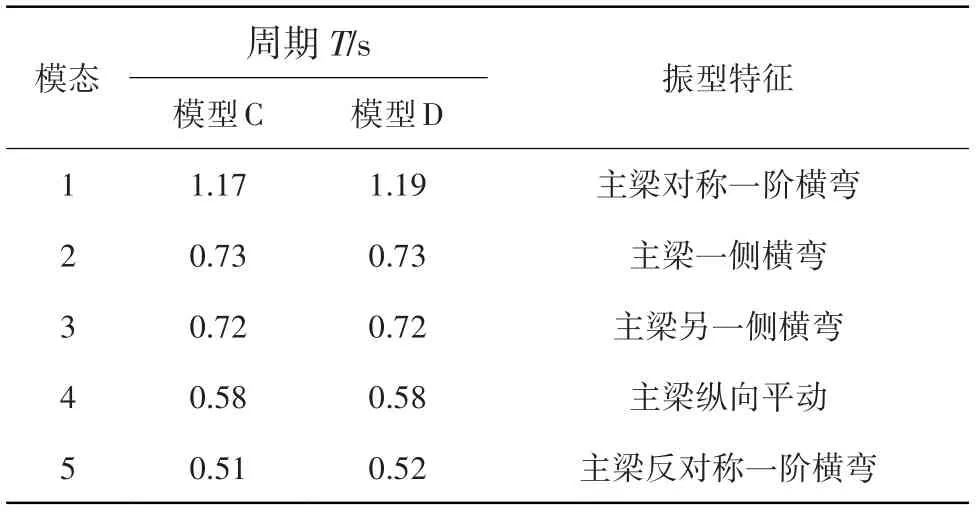
表4 拱肋对自振特性的影响Table 4 Effect of arch ribs on self-vibration characteristics

为了解拱肋对该桥横向地震反应的影响，在模型B、模型C和模型D基础上进行时程分析，图5给出了主梁关键部位的横向峰值位移，图6为模型B中主梁和拱肋的位移时程曲线，表5给出了可判定主梁和拱肋的横向位移模式的“横向位移变异系数”［21］，可以看出：

表5 主梁和拱肋横向位移变化系数（单位：%）Table 5 Coefficient of displacement variation of girder and arch ribs（unit：%）

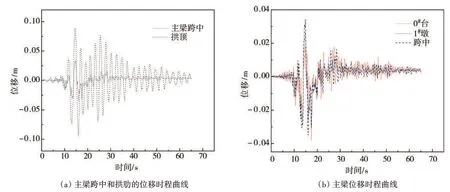
图5 位移时程曲线Fig.5 Displacement time-history curve of girder and arch ribs

图6 主梁关键部位的峰值位移Fig.6 Peak displacement of key position of girder

（1）连续梁拱桥（模型B）的主梁横向位移大于相等质量的连续梁桥（模型D），说明拱肋的存在放大了主梁的位移响应，主要是由于主梁与拱肋在地震作用下为同相运动，如图5（a）所示。

（2）图5（b）中主梁各关键位置的位移时程曲线基本相近，当主梁的位移较大时，关键部位的位移呈横桥向同相运动；主梁的横向位移变异系数远小于5%（表5），说明主梁的振动形式为横桥向的刚体运动；而拱肋的横向刚度较小，横向变异系数大于10%，发生弯曲变形的可能性较大，与表3中振型特征的分析结果一致。需要说明的是：图5（b）中位移很小时，可能存在异相运动，由于位移和结构响应很小，可以忽略。

（3）图6 中连续梁桥（模型D）与不考虑拱肋质量的连续梁拱桥（模型C）主梁横向位移基本一致，说明拱肋刚度对主梁变形的影响很小。

4 减震控制系统及其性能优化

为了控制连续梁拱桥的地震反应，基于功能分离的设计理念，发展“支座加耗能装置”的减震控制系统，通过滑动支座来控制主梁的竖向荷载，通过减震装置来控制主梁的水平向位移，甚至于实现自复位；组合减隔震控制系统包括：（1）减震榫和拉索限位器组合［23］。（2）SCEDB 和BRB 组合［12］。前者可以起到水平向耗能和限位的作用，后者可同时发挥两种支撑的优点，通过控制定义的无量纲参数自恢复力比ζ，可使整个体系达到最佳的减震和自复位效果。在无速度脉冲效应地震动作用下，SCEDB和BRB的组合形式按自恢复力比ζ=0.05来选定［12］，最终确定4根SCEDB和8根BRB组合的方式。减震榫采用和文献［22］相同的构件和参数，拉索限位器依据等强度原则，由相应的支撑总强度，推算出其力学参数。表2给出了4种减震装置的力学特性参数，经计算共需要12根减震榫和12根拉索限位器，沿纵桥向在桥墩两侧和桥台背墙内侧布置耗能支撑和拉索限位器。地震反应分析时，皆以40组地震动作用下反应峰值的平均值为讨论指标。

4.1 减震效果对比

在考虑轨道约束的情况下，模型E（减震榫-拉索限位器）的拉索沿纵桥向布置，模型F（SCEDB-BRB）的耗能支撑延45°方向布置。文中的连续梁拱桥其下部结构为重力式桥墩，桥墩的变形能力很小，水平变形主要集中于减震装置即主梁关键部位处，桥梁的震后功能可恢复性主要由减震控制系统的性能来体现。图7给出了布置两种组合减震系统后主梁关键部位的峰值位移和残余位移。

图7 主梁关键部位的峰值位移和残余位移Fig.7 Peak displacement of key positions of girder

从图7可以看出：减震榫和拉索限位器组合使用时的减震系统位移大于耗能支撑的组合系统，尤其是减震榫在横桥向的位移更大，接近于其极限位移（72 mm）［23］，这主要是由于该组合减震系统中拉索限位器仅对纵桥向起作用，而耗能支撑组合系统斜向布置时，沿纵桥向和横桥向皆可发挥作用。同样，对于铁路桥梁而言，减震榫横桥向的残余位移较大，是难以接受的，而耗能支撑组合系统几乎没有残余位移，即可实现自复位。

4.2 支撑布置角度分析

为了进一步了解支撑布置角度对减震效果的影响，故在模型F 的基础上，对支撑的布置角度（支撑轴线与主梁轴线夹角）在区间30°～60°之间划分了7种布置方式。由于主梁各位置处位移变化规律基本相同，故以0#桥台处主梁的位移响应为例进行说明。图8 给出了0#桥台处主梁沿横桥向和纵桥向的位移和残余位移，可以看出：

当布置角度在40°～45°时，主梁沿横桥向和纵桥向的位移都能控制在较小范围内，同时残余位移也较小。另外，考虑轨道约束对主梁沿纵桥向的峰值位移有明显的约束作用，而对横桥向的约束作用较小，图8（a）中考虑轨道约束后横桥向峰值位移减小的原因可能是钢轨的纵向连接对横桥向地震反应的耦合作用所致。

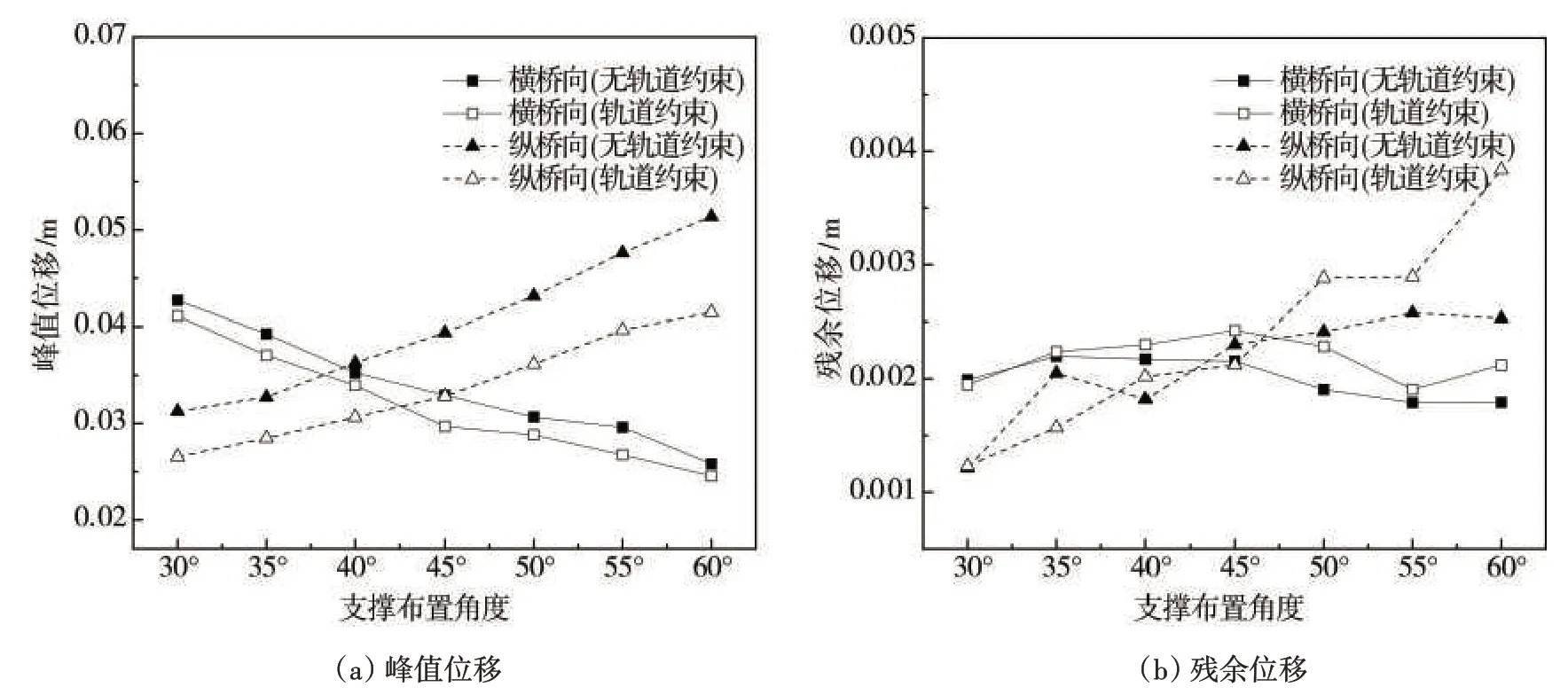
图8 0#桥台处主梁的位移响应Fig.8 Displacement response of girder at 0#abutment

在实际工程中，支撑布置角度应综合考虑两个方向的地震位移需求差异，以及结构或构件的变形能力与允许的变形范围。考虑到行车安全性等要求，铁路桥梁的横向地震峰值位移和震后残余位移限制较为严格。因此，该连续梁拱桥的耗能支撑布置角度宜在40°～45°。

5 结论

本文探讨了轨道约束和拱肋对铁路连续梁拱桥地震反应的影响；对比了两种减震系统的减震效果；分析了组合耗能支撑布置角度对减震效果的影响。由于拱肋对主梁位移反应的影响在实际工程中尚不明确，故文中数值模拟结果仅作为理论层次的讨论。主要得到以下结论：

（1）轨道约束对桥梁上部结构纵向动力特性的影响较大，一定程度上降低了纵桥向的地震反应。

（2）SCEDB-BRB组合减震效果在纵桥向和横桥向均表现出比减震榫-拉索组合更优异的减震效果。

（3）采用SCEDB-BRB 组合减震系统，当支撑布置角度在40°～45°时，主梁沿横桥向和纵桥向的位移都能控制在较小范围内；当SCEDB-BRB 的组合形式按自恢复力比ζ=0.05 分配时，残余位移可得到有效控制。建议综合考虑桥梁纵横向的地震位移需求及结构或构件允许的变形范围选择合适的布置角度。

附录A：地震动选取记录Table A1 Selected earthquake records