大学生体育健康测试综合评价研究

付文婧

目前很多高校会利用体育健康测试成绩得出学生体质健康及格率，并且该成绩会直接纳入学生全面素质教育发展体系。但是传统大学生体育健康标准测试所得成绩仍存在一定的人为因素的影响。如何改善人为因素影响，并通过利用统计方法和模型更新大学生体育健康标准测试是本研究需要解决的问题。

1 具体分析过程

1.1 研究对象及指标

以中北大学材料科学与工程学院380名女生为总样本量，评价指标为体育测试的6项指标：肺活量X1，立定跳远X2，坐位体前屈X3，50mX4，800mX5，1min仰卧起坐X6。

1.2 数据预处理及描述性分析

将380个总体单元编码，进行简单随机抽样（总体N中任意抽取n个个体为样本，各样本被抽中的概率相等），最后抽取样本量为30个（Excel随机生成编号），重新编号后即为本次的研究对象。由于X5，X6为逆向指标，令X5=100/S800，X4=1/S50（S为800m和50m用时，单位：秒），便于分析。

通过描述性统计分析得出，肺活量（X1）方差最大（为2142），说明该指标在各样本之间差距最大;而50m的方差（0.098）小于1，说明样本50m成绩之间相差不大。肺活量X1和立定跳远X2（130.0）方差排在第一第二，是学生体测成绩之间较好的区分指标。

1.3 因子分析的适用性

因子分析是指研究从变量群中提取共性因子的统计技术。利用KMO系数检验和Bartlett的球形度检（KMO系数需大于0.5，球形检验显著性需小于0.05）可判定是否适合使用因子分析模型。进行因子旋转，利用旋转后的因子载荷按照所含信息的百分比提取公因子（所含信息量称为信息贡献率一般需要大于70%，否则不适合用此方法进行因子提取），选取旋转载荷碎石图特征值大于1的公因子即为样本最后分类数。

利用SPSS进行数据分析，结果显示KMO（0.732）>0.7，球形检验显著性（<0.000）<0.05，通过相关系数矩阵检验。因子间相关系数基本都>0.3，说明30个样本间存在较强的相关关系，适合做因子分析。通过因子分析旋转提取出的两个因子F1和F2（碎石图特征值分别为2.683和1.167，图一所示）用来代替原来6个指标解释学生体育测试水平，提取的信息总量（累计贡献率）为77.168%，含有较大的信息量。

通过旋转后的成分矩阵，得出因子对初始6项指标的解释程度，F1对指标立定跳远X2、50mX4、800mX5和1min仰卧起坐X6解释程度较大，F2对指标肺活量X1和坐位体前屈X3的解释程度较大。命名第一因子为运动型因子（F1），第二因子为素质型因子（F2）。利用得分方程函数公式：

（i为提取公因子个数，j为原有因子个数，a为旋转矩阵系数），利用旋转后成分矩阵得到系数，最终得分方程如下：

F1=0.228X1+0.606X2+03606X3+0.855X4+0.832X5+0.864X6

F2=0.789X1-0.1X2-0.688X3+0.221X4-0.1X5-0.029X6

根据共因子得分，以特征值所占比例为权数（权重分别为0.697，0.303），计算综合因子得分。计算公式为：

将原始数据进行标准化后，因子得分的平均值为0，故离0越远因子得分越突出。综合得分后得到优、良、中、差四个等级，得分由差到优分别为：（-∞，-1），（-1，0），（0，1）和（1，∞）。对比初始测试标准的成绩，得出5个差异较大的异常值如表二所示。主要原因为，25号样本由于在运动型因子方面得分较低，所以在新的标准中该因子得分较低;而10号、12号、18号由于在运动型因子上得分较高，故综合得分较高。可以看出，运动型因子是第一因子，因子贡献率为54.723%，远高于素质型因子，所以在统计标准测试中占主导地位。

1.4 结果验证

1.4.1 K均值聚类法检验

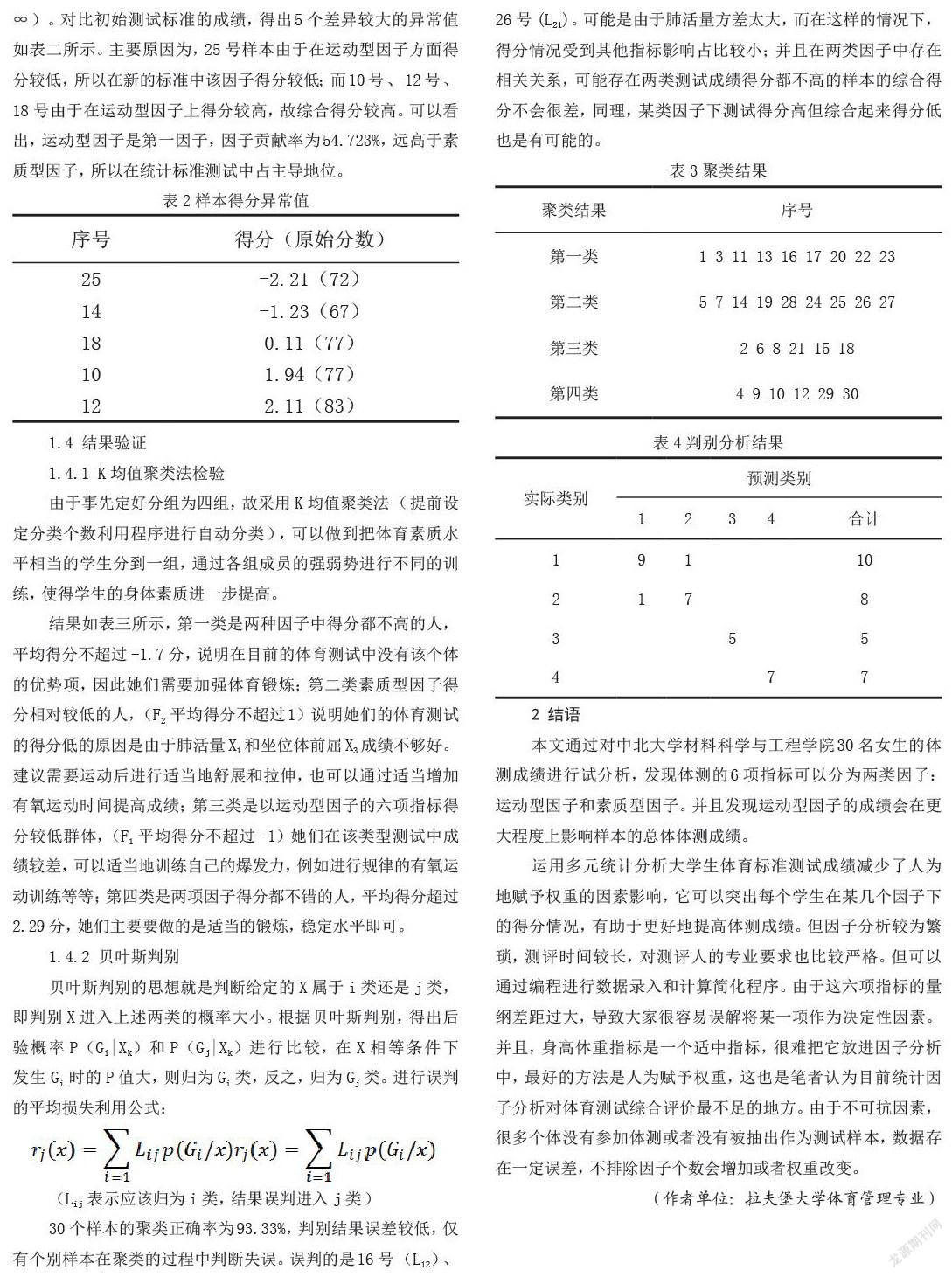
由于事先定好分组为四组，故采用K均值聚类法（提前设定分类个数利用程序进行自动分类），可以做到把体育素质水平相当的学生分到一组，通过各组成员的强弱势进行不同的训练，使得学生的身体素质进一步提高。

结果如表三所示，第一类是两种因子中得分都不高的人，平均得分不超过-1.7分，说明在目前的体育测试中没有该个体的优势项，因此她们需要加强体育锻炼;第二类素质型因子得分相对较低的人，（F2平均得分不超过1）说明她们的体育测试的得分低的原因是由于肺活量X1和坐位体前屈X3成绩不够好。建议需要运动后进行适当地舒展和拉伸，也可以通过适当增加有氧运动时间提高成绩;第三类是以运动型因子的六项指标得分较低群体，（F1平均得分不超过-1）她们在该类型测试中成绩较差，可以适当地训练自己的爆发力，例如进行规律的有氧运动训练等等;第四类是两项因子得分都不错的人，平均得分超过2.29分，她们主要要做的是适当的锻炼，稳定水平即可。

1.4.2 贝叶斯判别

贝叶斯判别的思想就是判断给定的X属于i类还是j类，即判别X进入上述两类的概率大小。根据贝叶斯判别，得出后验概率P（Gi|Xk）和P（Gj|Xk）进行比较，在X相等条件下发生Gi时的P值大，则归为Gi类，反之，归为Gj类。进行误判的平均损失利用公式：

30个样本的聚类正确率为93.33%，判别结果误差较低，仅有个别样本在聚类的过程中判断失误。误判的是16号（L12）、26号（L21）。可能是由于肺活量方差太大，而在这样的情况下，得分情况受到其他指标影响占比较小;并且在两类因子中存在相关关系，可能存在两类测试成绩得分都不高的样本的综合得分不会很差，同理，某类因子下测试得分高但综合起来得分低也是有可能的。

2 结语

本文通过对中北大学材料科学与工程学院30名女生的体测成绩进行试分析，发现体测的6项指标可以分为两类因子：运动型因子和素质型因子。并且发现运动型因子的成绩会在更大程度上影响样本的总体体测成绩。

运用多元统计分析大学生体育标准测试成绩减少了人为地赋予权重的因素影响，它可以突出每个学生在某几个因子下的得分情况，有助于更好地提高体测成绩。但因子分析较为繁琐，测评时间较长，对测评人的专业要求也比较严格。但可以通过编程进行数据录入和计算简化程序。由于这六项指标的量纲差距过大，导致大家很容易误解将某一项作为决定性因素。并且，身高体重指標是一个适中指标，很难把它放进因子分析中，最好的方法是人为赋予权重，这也是笔者认为目前统计因子分析对体育测试综合评价最不足的地方。由于不可抗因素，很多个体没有参加体测或者没有被抽出作为测试样本，数据存在一定误差，不排除因子个数会增加或者权重改变。

（作者单位：拉夫堡大学体育管理专业）