全概率公式和贝叶斯公式的教学研究

贺 莎

（北京第二外国语学院基础科学部，北京 100024）

全概率公式和贝叶斯公式是《概率论与数理统计》课程中非常重要的两个公式，它们被安排在条件概率和乘法公式后进行学习，它们形式上非常抽象复杂，通常用来计算复杂的随机事件的概率。学生在第一次接触这两个公式时，会感到难以理解，十分难记，搞不清公式中各种符号的含义。所以，笔者在课堂讲授这两个公式时，为了使学生易于理解，会先通过一道与学生生活密切相关的引例引入这两个公式，对公式进行深入分析后，再将它们应用于解决著名的历史典故问题。让学生不仅深刻理解这两个公式的含义并会灵活运用，还发现数学是来源于生活，又应用于生活的，是对生活中事物的统一规律的抽象总结，拔高了整堂课的育人目标高度。

1 引入问题

引例小明的钥匙丢了，可能的丢失地点为食堂、宿舍和教学楼，概率分别为0.4，0.1，0.5，而掉在上述三个地方钥匙被找到的概率分别为0.4，0.9，0.3，求找到钥匙的概率。又若钥匙被找到，求它最可能在上述三个地方的哪一个被找到？

课堂一开始以一道与学生生活密切相关的问题作为引例，增加学生强烈的好奇心，他们迫切地想知道找到钥匙的概率以及最有可能在什么地方找到，激发学生的研究探索兴趣，从而引出本节课的课程内容——全概率公式与贝叶斯公式，这样学生便会有目的地听课。

2 剖析问题

在介绍全概率公式前，先带学生回顾之前学的完备事件组的概念。设是样本空间，完备事件组就是指同时满足(1)两两互斥；(2)这两个条件的事件组随机事件组。例如，下图中的就是一个完备事件组。

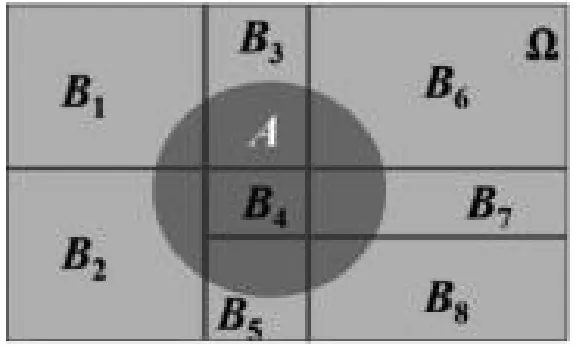
全概率公式通常用来计算复杂事件的概率，想法是把复杂事件拆分成两两互斥的简单事件的和，再用乘法公式计算每一个简单事件的概率，最后再把这些简单事件的概率相加，就得到复杂事件的概率。特别地，若完备事件组只由两个随机事件和它的对立事件组成，则对任一随机事件，这是全概率公式的最简单的形式，也板书写在黑板上。

下面我们来解决引例的第一问，即求找到钥匙的概率。由题意可知钥匙掉在食堂、钥匙掉在宿舍和钥匙掉在教学楼这三个随机事件构成了一个完备事件组，要计算找到钥匙的概率，根据全概率公式，我们只需知道钥匙掉在以上三个地方的概率以及如果掉在这三个地方钥匙分别被找到的概率，而这些信息均由题意可得，从而把它们对应相乘再相加起来，即为钥匙被找到的概率，第一问得解。

接着我们来考虑第二问，假如钥匙被找到，它最可能在上述三个地方的哪一个被找到？由此引入本节课的另一个内容——贝叶斯公式。

如果把钥匙被找到看成已知结果，把钥匙掉在食堂、钥匙掉在宿舍和钥匙掉在教学楼看成原因，那么在已知结果的条件下，要寻求最可能发生的原因，只需将各个原因发生的概率进行对比即可。下面我们先来推导计算这些概率的贝叶斯公式。和全概率公式的假设一样，设是一个完备事件组，是任意一个随机事件，现在在已知事件发生的条件下，求导致它发生的原因的概率，即求条件概率由条件概率公式可得，对分子用概率的乘法公式，对分母用全概率公式，于是得到

上式由英国数学家托马斯贝叶斯（Thomas Bayes，1702-1761）最早发现的，现在，它已在信用问题、疾病早期诊断的解释等方面发挥着重要的作用，人们将它称为贝叶斯公式[1-3]。此时，在黑板上板书写上该公式，这是本堂课的重难点内容之二。

要解决第二问，我们只需根据贝叶斯公式算出若钥匙被找到，它在食堂、宿舍和教学楼这三个地方找到的概率，而在该公式中，分子分母中的每一项均可由题意得到。注意到，贝叶斯公式的分母其实是全概率公式的应用，已在第一问算出；而它的分子是分母求和当中的某一项，也已知。从而将各项代入公式算出概率后，再比较这三个概率的大小，得出结论，至此第二问得解。

3 解决问题

学习了全概率公式和贝叶斯公式后，根据上面的分析，现在我们利用它首先来解决找到钥匙的概率问题。设事件A={找到钥匙}，事件={钥匙掉在食堂}，事件={钥匙掉在宿舍}，事件={钥匙掉在教学楼}，则是一个完备事件组，且由题意于是将它们代入全概率公式可得

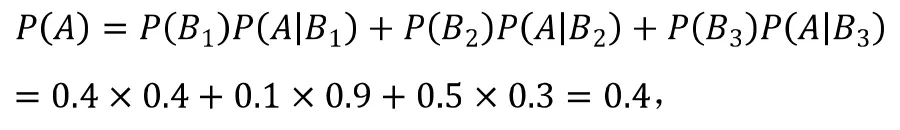
即钥匙被找到的概率为0.4。

再来解决若钥匙被找到，它最有可能在哪里被找到的问题。根据贝叶斯公式，我们可求得若钥匙被找到，则它在食堂、宿舍和教学楼找到的概率分别为

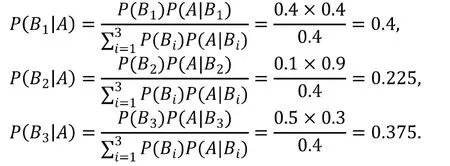
4 总结问题

全概率公式可看成“由原因推结果”，已知各个原因发生的概率，计算这些原因产生的结果的概率；而贝叶斯公式的作用是“由结果倒推原因”，在已知一个结果发生的条件下，在众多可能的原因中，推算出该结果最有可能是哪个原因造成的，故贝叶斯公式也称为“逆概公式”。

5 应用公式

例（历史典故“烽火戏诸侯”）西周末年，周幽王为博得妃子褒姒一笑，听信了佞臣的谗言，点燃了烽火台，诸侯们以为有敌寇侵入，纷纷带领大军从各地赶来都城镐京帮忙，结果发现周幽王一众人在饮酒作乐，诸侯知道被戏弄，带着怨恨返回，褒姒见浩浩荡荡的千军万马招之即来，挥之即去，觉得十分好玩，禁不住微微一笑。周幽王见状非常高兴，为了让褒姒多笑，后来他又多次点燃烽火，导致诸侯们都不相信烽火，也就渐渐不来了。后来敌寇犬戎真的攻破镐京，杀死了周幽王，自此西周灭亡。

试用贝叶斯公式分析该典故中诸侯受骗两次后对周幽王的可信度是如何下降的。

诸侯第一次受骗后，他们对周幽王的可信度变为

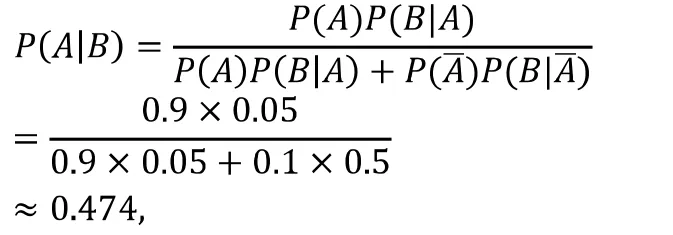
即在诸侯被骗了一次这件事情发生后，诸侯对周幽王的可信度降为

诸侯第二次受骗后,他们对周幽王的可信度变为

所以经过两次受骗后，诸侯对周幽王的可信度由最初的0.9下降至0.083，当真有犬戎进攻镐京，周幽王点燃烽火台时，诸侯们再也不来帮他了。

所以本题从概率论的角度解释了与诚信紧密相关的历史典故，让学生有豁然开朗的感觉，不禁连连感叹原来数学还能这么用！类似的例子还有伊索寓言的“狼来了”，“银行贷款未还影响个人信用度”等，通过这些实例，对学生进行了一次深刻的诚信教育。在讲授完这个例子后，相信学生已经深刻理解了贝叶斯公式及其应用，也对他们的思想进行了一次洗礼。[4-5]

6 结语

从整体上来看，在本堂课的课程教学中，采用“案例教学法”，通过与学生生活密切相关的问题作为例子引入，吸引学生注意力，激发学生强烈的学习兴趣，使他们带着问题来学，更加具有目的性。课程设计以问题为导向，以分析为重点，以应用为巩固拓展，引导学生思考、解决问题。在分析问题时很自然地推导出了全概率公式和贝叶斯公式，非常清楚地解释了这两个公式的来龙去脉，加深了学生对全概率公式和贝叶斯公式的理解，然后应用这两个公式解决了引例的问题。再用所学公式从概率论角度分析解释烽火戏诸侯这个我国著名的历史典故，在讲授新内容的同时并对学生进行一次深刻地诚信教育，既教他们用贝叶斯公式来分析解决实际问题，深刻体会了数学的重要性，增加了课堂的趣味性，又将课程思政很自然地融入课堂教学中，真正做到了教师寓教于乐，学生寓学于乐，提高了课堂教学的效率。