数学分析教学中关于三角函数定义的探讨

雷 力

（重庆师范大学数学科学学院，重庆 401331）

三角函数是数学分析课程中重要的基本初等函数之一。在很多数学分析、高等数学教材中，三角函数的定义都是沿用中学数学的定义[1-2]。

在初中数学课程中，我们是用直角三角形的各边长之比来定义三角函数的，直角三角形的一个锐角的对边与斜边之比称为这个角的正弦，它的邻边与斜边之比称为这个角的余弦。在高中数学课程中，我们又将三角函数的定义域从锐角推广到了任意角。建立平面直角坐标系xOy，将射线Ox绕原点O旋转 角，角的正负由旋转方向所决定，逆时针旋转为正，顺时针旋转为负，设所得射线与圆心在O点的单位圆相交于点A。我们定义角 的正弦为点A的纵坐标，角 的余弦为点A的横坐标。我们知道，平面上任意一点绕原点O旋转180°所到的位置与原来的位置关于O点对称，任意一点绕原点O旋转360°就回到原来的位置。所以正弦函数与余弦函数都是周期函数，并且自变量每增加半个周期函数值就改变一次符号。

在数学研究中，我们通常使用弧度制来衡量角的大小，所谓弧度制是用弧长与半径之比作为对应圆心角的角度。这样，任意一个角就可以用一个实数来表示它的大小，而正弦函数与余弦函数则是定义在整个实数集上的实值周期函数。

然而前面所述的三角函数定义是高度依赖几何直观的，其中角的构成我们用到了“旋转”这样的平面变换，角的大小我们用了圆弧的长度来度量。这些是我们还未曾定义的概念。数学分析这门课程，是以实数理论为基础的对古典微积分的严格化。因此，在数学分析课程中采用中学数学的三角函数定义是不严密的.本文将通过定积分给出三角函数一个分析上严格的定义。

接下来我们考虑如何严格定义余弦函数与反余弦函数.如图1所示，设上半平面，坐标为。则弧的方程为

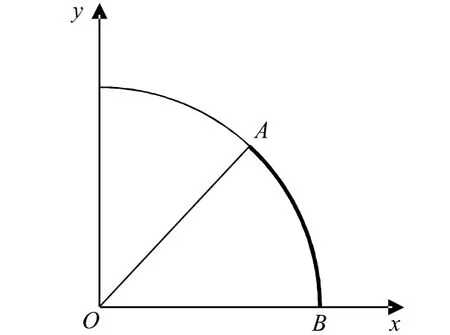
图1

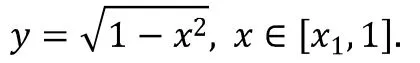
这是一个无界函数的反常积分，由比较判别法可知它是收敛的。

一些数学分析教材采用幂级数展开式(11)与(12)作为正弦函数与余弦函数的定义[3][4]。前面的推导过程表明这种使用幂级数展开式给出的定义与我们通过定积分给出的定义是一致的。但正弦函数与余弦函数的幂级数定义体现不出它们的几何意义，本文所采用的定义不仅具备严格性，也保留了三角函数的几何直观。