基于对数极坐标和频域率的互信息图像配准∗

徐永会 杨德智 刘芳名

（陆军炮兵防空兵学院 合肥 230031）

1 引言

基于傅立叶变换的相位相关算法因运算速度快且准确，广泛应用于图像配准。由Chen和Reddy等提出的基于Fourier-Mellin变换的算法［1］，对产生位移、尺度变异的图像配准效果较好，但在处理旋转、缩放图像时，与匹配参数对应正确度差。后由Stone等提出“旋转引起混叠影响对配准精度”的观点［2］，有效解决了360°范围内的旋转参数求解问题。本文将Fourier-Mellin变换与互信息相结合，提出在对数极坐标和频率域中寻求最大互信息进行图像配准。

2 傅立叶变换及相位相关法

基于傅立叶变换的相位相关法是通过傅立叶变换，实现图像的空域变换到频域，数据运算随之转为频率域乘法运算［4］。根据在空域上图像平移在频率域中表现为相位差的特性，计算两幅图像的互功率谱，从而得到图像的位移量。

假设两幅图像 f1(x,y)和 f2(x,y)，f2(x,y)是f1(x,y)由经过简单的平移(x0,y0)得到，即：

根据傅立叶变换的性质可得：

式中 F1(μ,ν)和 F2(μ,ν)分别为 f1(x,y)和 f2(x,y)的傅立叶变换。它们的互功率谱为

通过对互能量谱进行傅立叶反变换，得到的单位脉冲函数δ(x-x0,y-y0)，根据该函数出现的尖锐峰值，求得图像的相对平移量x0和 y0。函数式经过傅立叶反变换，生成脉冲峰值群，而最大峰值对应的位置，就是要求得的相对平移量，这种方法称为Fourier相位相关法［5］。

3 对数极坐标变换

在进行图像配准采用对数极坐标变换时，将图像点完成由直角坐标系向对数极坐标系映射后，图像的尺度与旋转保持不变，由此分析解决问题［5］，如图1所示。以直角坐标系中图像的中心点为原点，以到中心点的极距ρ和极角θ为坐标轴，对极距ρ取对数，得到图像的对数极坐标。从图像的直角坐标(x,y)映射到对数极坐标(log(ρ),θ)。图像的任意一点(x,y)都可表示为

极坐标变换，如图1（a）为图像的直角坐标表示，图像的极坐标表示如图1（b）。图1（a）中区域A、B、C表示相同的极角所对应的图像区域，图1（b）对应相同的纵坐标 θ 值；图1（a）中区域D、E、F表示相同的极距所对应的图像区域，在图1（b）对应相同的横坐标ρ值。

图1 直角坐标到极坐标的映射表示

将上述图像的极坐标系转换到对数极坐标系，纵轴极角θ不变，横坐标极距ρ取对数得到γ，即γ=log(ρ)。在图1（a）中将图像放大 λ倍，对应的图（b）中沿横轴方向放大λ倍；在对数极坐标中，由γ=log(ρ)得，有 γ=log(λρ)=log(λ)+log(ρ)，即图像沿横轴γ移动了log(λ)。综上所述，经对数极坐标变换后，图像在对数极坐标系中具有保持尺度与旋转不变的特性。

据此总结，图像由直角坐标系变换为对数极坐标系，是均匀性向非均匀的转换，需要离散化处理距离轴，即首先将像素点从直角坐标系变换到极坐标系，再映射为横轴γ；角度轴映射是将一组径向直线均匀映射为 θ 轴［6］。

4 基于对数极坐标变换的相位相关法

当两幅图像只存在缩放尺度和旋转变换时，可以将图像对数极坐标系下进行傅立叶变换和相位相关计算［7］，得到图像的缩放尺度和旋转角度。

设两图 f1(x,y)和 f2(x,y)在直角坐标系中尺度变换参数为λ、旋转变换角度为φ：

经对数极坐标变换：

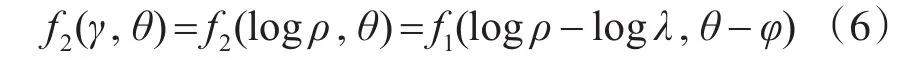
从上式中可以看出，经过对数极坐标变换后f2(logρ,θ)相对于 f1(logρ,θ)只存在平移关系，因此，可以利用相位相关法［7］获得logλ和旋转角度φ，进一步获得缩放尺度λ和旋转角度φ。

5 基于Fourier-Mellin变换的图像配准

设两图 f1(x,y)和 f2(x,y)在直角坐标系中平移变换(x0,y0)、尺度变换λ、旋转变换角度φ：

对 f1(x,y)和 f2(x,y)进行图像配准的步骤［8～10］如下：

1）根据傅立叶平移、旋转和缩放定理：进行傅立叶变换，得到 F1(μ,ν)和 F2(μ,ν)。

2）对 F1(μ,ν)和 F2(μ,ν)进行高通滤波处理，得到F′1(μ,ν)和 F′2(μ,ν)。

3）对 F′1(μ,ν)和 F′2(μ,ν)求模计算，得到幅度谱 M1(μ,ν)和 M2(μ,ν)。

4）对幅度谱 M1(μ,ν)和 M2(μ,ν)进行对数极坐标变换，得到 LPM1(ξ,θ)和 LPM2(ξ,θ)。

因此采用相位相关算法［7］可求得d和φ，再通过变换即可得到尺度因子λ和旋转角度φ。

5）计算 LPM1(ξ,θ)和 LPM2(ξ,θ)的互功率谱，得到缩放尺度λ和旋转角度φ。

根据傅立叶变换的平移特性，计算LPM1(ξ,θ)和LPM2(ξ,θ)的互功率谱。先进行傅立叶变换，得到 FLPM1(μ,ν)和 FLPM2(μ,ν)，再由 LPM2(ξ,θ)=LPM1(ξ-d,θ-φ)可得：

互功率谱为：

FLPM*2(μ,ν) 为 FLPM2(μ,ν) 的 复 共 轭 ；e-j(μd+νϕ)的 傅 立 叶 反 变 换 为 二 维 脉 冲 函 数δ(x-d,y-ϕ)，该函数偏移位置有明显的尖锐峰值，据此特性相对平移量d和φ，得到缩放尺度λ=ed，旋转角度φ。

6）根据缩放尺度 λ和旋转角度φ，对图像f2(x,y)进行缩放、旋转变换，得到 f′2(x,y)

7）计算 f1(x,y)和 f′2(x,y)的互功率谱，得到平移参数(x0,y0)。

根据傅立叶变换的性质［5］可得：

互功率谱为

8）对 f2(x,y)以平移(x0,y0)、缩放 λ、旋转 φ进行变换，得到配准后的图像 f″2(x,y)。

6 引入互信息Fourier-Mellin变换的图像配准

上述的Fourier-Mellin变换在图像变换参数较小时，具有良好的配准效果。当图像缩放尺度变大时，导致Fourier-Mellin系数失真。为此，对Fouri⁃er-Mellin变换进行改进，引入互信息计算［11～12］，通过寻求最大互信息，得到平移参数，继而计算出缩放和旋转参数，计算过程如图2所示。

图2 基于对数极坐标和频率域的互信息图像配准流程图

1）在参考图像 f1(x,y)中心片截取一个小的区域I1(x,y)；

2）计算 I1(x,y)的对数极坐标变换 T1(γ,θ)及其对应的傅立叶变换 F1(μ,υ)；

3）在待配准图像 f2(x,y)中任意位置，以(x,y)为中心截取大小相同的小区域I2(x,y)；

4）计算 I2(x,y)的对数极坐标变换 T2(γ,θ)及其对应的傅立叶变换 F2(μ,υ)；

5）计 算 F1(μ,υ) 和 F2(μ,υ) 的 互 功 率 谱P(μ,ν)，再对互功率谱作傅氏反变换 A(γ,θ)；

6）在 A(γ,θ)中找出数值最大的位置 (λ,φ)及其数值σ，以 A(γ,θ)为大小构建一个脉冲位置在(λ,φ) ，大 小 为 σ 的 理 想 二 维 脉 冲 信 号B(γ-λ,θ-φ)。

7）计算 A(γ,θ)和 B(γ-λ,θ-φ)的互信息，得到互信息量H。

8）取互信息量H最大值所对应的I2(x,y)的中心位置(x0,y0)和二维脉冲位置(λ0,φ0)，则得到待配准图像的平移参数为(x0,y0)，缩放尺度为，旋转角度为φ0。

9）根据得到的图像平移、缩放、旋转参数，对图像 f2(x,y)进行相似变换，求得 f′2(x,y)。

7 实验结果与分析

为检验改进后的图像配准算法的有效性，对引入互信息Fourier-Mellin变换的图像配准（简称改进算法）与标准的基于Fourier-Mellin变换图像配准（简称标准算法）进行比较，设计如下实验。在Intel® Core™2 Quad CPU Q8400@2.66GHZ、2.00GB内存的个人计算机，操作系统为Windows XP，用Matlab编程语言。对同时存在旋转、缩放和平移变换关系的Bomb图像进行图像配准测试。如图3（a）为大小为 352×288Bomb的灰度图像，图3（b）、图 3（c）、图3（d）为3幅待配准 Bomb图像，分别称为Bomb1、Bomb2、Bomb3。它们均是在原 Bomb图像基础上进行缩放、旋转和平移变换得到的，变换参数如表1所示。分别采用上述改进算法和标准算法，得到结果如表2所示。

图3 用于实验的Bomb图像

表1 三幅待配准图像相对原始图像的变换参数

表2 不同变换参数下标准算法与改进算法的图像配准结果比较

从表1和表2可得如下几点：

1）两种算法的图像配准精度都随着图像变换系数的变化而变化，随着缩放比例、旋转角度和平移量的增大，配准后的误差逐渐增加，图像配准精度逐渐减小。

2）当图像变换系数相同时，不论图像缩放比例、旋转角度和平移量是多少，引入互信息的算法都比标准Fourier-Mellin变换的图像配准算法精度高。

8 结语

图像配准是战场图像处理的基本问题，基于傅立叶变换的相位相关方法是图像配准研究的重要方法。本文主要从提高图像配准算法精度的角度，对标准Fourier-Mellin变换的图像配准进行了分析，提出了将互信息引入其中，形成了一种新的基于对数极坐标和频率域的互信息图像配准算法，提高了图像配准精度。