基于压缩感知的OFDM系统信道估计方法

李贵勇，吕京昭，陈 博，秦 红，方泽圣

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)作为一种多载波调制技术，已成为宽带无线通信的核心技术。在OFDM系统中，接收端需要获取信道状态信息(Channel State Information，CSI)用来恢复发送的信号，因此对信道估计技术的研究十分重要。

传统的信道估计方法，如最小二乘(Least Squares，LS)[1]和最小均方误差(Minimum Mean Square Error，MMSE)[2]算法虽然复杂度较低，但由于巨大的导频开销导致频带利用效率降低。2006年，Donoho等人提出了压缩感知(Compressed Sensing，CS)理论[3-5]，该理论表明，当信号是稀疏的或可压缩的时，可以从有限的样本值中重建信号；正交匹配追踪(Orthogonal Matching Pursuit，OMP)[6]算法是一种经典的贪婪算法，其可以通过较少的计算量可靠地重建信号；正则化正交匹配追踪(Regularized Orthogonal Matching Pursuit，ROMP)[7]算法一次可以选择多列原子，再通过正则标准筛选，可实现原子快速和有效地选择；压缩采样匹配追踪(Compressive Sampling Matching Pursuit，CoSaMP)[8]算法每次迭代选择的原子可能会在下一次迭代中被丢弃。但以上算法的弊端是需要已知信道稀疏度，稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit, SAMP)[9]算法不需要将稀疏度作为已知条件，但该算法通过固定步长估计稀疏度，会出现欠估计和过估计问题。

针对实际信道稀疏度未知的情况，本文提出了一种基于Dice系数的稀疏度自适应正交匹配追踪(Sparsity Adaptive Dice Orthogonal Matching Pursuit，SADOMP)算法，该算法不需要已知信道稀疏度，且性能要优于经典信道估计算法。

1 OFDM系统模型

OFDM系统通过在发送端插入已知的导频信号辅助信道估计，发送端添加循环前缀(Cyclic Prefix，CP)的过程是将每个OFDM符号末端的一段信号复制到此符号的头部，这样可以保证系统子载波的正交性，从而消除了信道多径效应引起的符号间干扰(Inter Symbol Interference，ISI)和载波间干扰(Inter-Carrier Interference，ICI)，CP长度一般要大于信道冲激响应长度。OFDM系统接收端是对发送端的一个逆过程处理。OFDM系统模型如图1所示。

一个无线信道离散时间信道模型可表示为

式中：h(n)为信道脉冲响应；L为信道长度；αi为第i个多径信号的复数比例因子；δ()为冲激函数；n为采样点数；τi为第i个多径信号的到达时间。通过此信道模型发送信号会导致接收端收到L个多径信号的叠加，从而导致信号衰落和信号失真。在实际的无线信道中，h(n)是由少量的非零抽头系数组成，即信道具有稀疏性。

假设OFDM系统有P个导频信号，放置在k1、k2、k3、…、kP子载波上，一般导频信号是均匀地放置在数据信号中，即已知导频信号的位置信息，则接收端通过导频信号的位置信息可以提取导频信号：

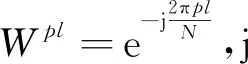
2 CS和重建算法

2.1 CS理论

实际环境中的信号一般不是绝对稀疏的，只要选择用适当的稀疏基表示高维信号，就可以通过有效的算法从高度不完整的线性测量中恢复高维信号。信号x可以通过引入稀疏基矩阵表示为x=Ψθ，Ψ为N×N维的稀疏基矩阵，θ为N×1的列向量，表示稀疏基Ψ下的稀疏信号，当θ中的非零元素个数K满足K≪N时，则称信号x是相对于稀疏基Ψ的K-稀疏信号。

当信号满足稀疏性时，通过构建观测矩阵，能够以远远小于信号维度的数据无失真或较低失真的方式重建原始信号。用公式表达如下：

式中：y为M×1维的测量信号；Φ为M×N维的观测矩阵(满足M≪N)；w∈RN为噪声向量；A为M×N维的传感矩阵。

由于M≪N，所以式(3)是一个欠定方程，有无穷多个解，但当信号x满足稀疏条件时，上述欠定方程可以转化成最小l0范数问题来求解。当N很大时，最小l0范数问题计算复杂度很大，是一个非确定多项式(Non-deterministic Polynomial，NP)问题。文献[10]指出可将这个问题转化成容易求解的最小l1范数问题，即min||x||1，s.t.y=Φx。文献[11]指出，当传感矩阵A满足等距约束性(Restricted Isometry Property，RIP)条件时，可以准确地恢复原始信号，满足RIP准则的条件为(1-δk)‖x‖2≤‖Φx‖2≤(1+δk)‖x‖2，式中，δk为常数，且δk∈(0,1)。

2.2 基于SADOMP的信道估计方法

2.2.1 DFT信道估计

DFT信道估计算法的具体做法是将LS算法估计得到的信道频率响应转换到时域，保留CP内的信号，将CP外部的信号清零。然后再将信道响应值转换到频域。考虑到CP内部也存在噪声的影响，算法通过设置阈值来区分CP中的有效点和噪声点，进一步提高DFT算法消除噪声的性能。算法流程图如图2所示。

图2 DFT信道估计算法流程

首先，通过LS算法获得信道频域响应HLS，再通过N点离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)获得时域的信道冲激响应hLS：

式中，w(n)为噪声。将CP长度之外的信道脉冲响应置为零，对于CP内部，通过以下方式设置阈值区分噪声信号和有效信号：

式中：LCP为CP的长度；σ1为循环长度内信道冲激响应幅度的平均值；σ2为循环长度外信道冲激响应幅度的平均值；σ为最终的阈值，是σ1与σ2之和。于是，信道的冲激响应可表示为

再将hLS(n)做DFT得到信道频域响应HDFT。

2.2.2 Dice系数匹配准则

经典的贪婪追踪算法中常用内积准则来度量残差向量与传感矩阵原子的相似度，内积值越大，说明相似度越高。假设两个N维向量a和b，内积准则的定义如下：

内积准则实质上是通过计算残差向量和传感矩阵挑选出来的原子的夹角余弦值来度量两个向量的相似度，但内积准则的问题在于，匹配过程中会丢失原始信号的部分信息导致匹配不准确。针对这个问题，引入Dice系数准则：

对比式(7)和(8)可知，内积准则的分母是对向量分量的平方和求几何平均值，Dice系数准则的分母是对向量分量的平方和求算数平均值。由于算术平均可以有效解决几何平均在匹配过程中丢失原始信号部分信息的问题，更好地保留信号的原始信息，因此基于Dice系数准则挑选出的原子是更优的，可以提高算法的恢复精度。

2.2.3 算法流程

输入：观测向量y，传感矩阵A，DFT估计的信道频域响应HDFT。

(1) 初始化：迭代次数t=1，初始残差r0=y，初始索引集Λ0=∅，初始原子支撑集A0=∅，初始残差与HDFT之差β0=0；

(2) 利用Dice系数匹配准则计算传感矩阵A的每一列向量与当前残差rt-1之间的相关系数：gt=abs[D(rt-1,AT)]，abs()为取绝对值，D()为Dice系数匹配函数，选择最大的一个并找到该系数对应A的列序号λt，即λt=arg max|D(rt-1,AT)|；

(3) 更新索引集和原子集：Λt=Λt-1∪{λt}，AΛt=AΛt-1∪{aλt}，其中，aλt为矩阵A的第λt列；

3 仿真结果及分析

为了验证SADOMP算法的有效性和可靠性，本文采用Matlab软件进行仿真实验，首先进行Dice系数准则可行性验证，然后对比本文算法与传统LS算法和CS OMP算法的误码率(Bit Error Rate，BER)和归一化均方误差(Normalized Mean Square Error，NMSE)性能。所有结果都是经过5 000次仿真后求得的平均值。仿真参数设置如表1所示，调制方式为正交相移键控(Quadrature Phase Shift Keying，QPSK)，OMP算法在信道稀疏度未知时，将其迭代次数设置为导频数的一半[12]。

表1 仿真系统参数设置

3.1 Dice系数准则可行性验证

可行性验证实验分别使用内积准则和Dice系数准则对传感矩阵原子和残差向量进行匹配，随机生成稀疏度K=8、长度N=1 024的一维信号，用32×1 024维FFT矩阵作为观测矩阵，对比在不同迭代次数下，残差向量模的变化。结果如图3所示。

图3 Dice系数准则和内积准则在迭代中残差向量模对比

由图可知，随着迭代次数的增加，残差向量的模逐渐减小。同时，使用Dice系数准则匹配得到的残差值比同等条件下内积准则的更小，证明使用Dice系数准则挑选出来的原子更优，能够加速迭代，提高重构效率。

3.2 NMSE性能分析

图4对比了本文所提SADOMP算法和LS算法、OMP算法在导频数为32时不同信噪比(Signal to Noise Ratio, SNR)下的NMSE性能。由图可知，随着SNR的增加，各种算法的NMSE均呈下降趋势，在低SNR情况下，3种算法的重构性能都较差。随着SNR的升高，SADOMP算法的NMSE性能明显优于其他两种算法，与LS和OMP算法相比，本文所提SADOMP算法分别约有10和5 dB的SNR峰值增益。充分验证了基于Dice系数准则的SADOMP算法信道估计的NMSE性能。

图4 不同算法NMSE曲线对比图

图5对比了SNR为15 dB时，3种算法在不同导频数下的NMSE性能。由图可知，随着导频数量的增加，3种算法的NMSE性能均得到提高，这是由于，导频数量越多，传感矩阵中包含的原始信息就越多，重构信号的效果就更好。在导频数量相同的条件下，SADOMP算法的NMSE性能明显优于LS和OMP算法；当NMSE相同时，本文所提算法需要的导频数量明显小于另外两种算法，可以说明在相同的重构精度下，本文所提算法能够减少导频的开销。

图5 不同导频数下各算法NMSE曲线对比图

3.3 BER性能分析

图6对比了在不同SNR情况下，3种算法的BER性能。由图可知，随着SNR的增加，3种算法的BER均呈下降趋势，在导频数相同的条件下，本文所提算法比OMP和LS算法有更低的BER。

图6 不同SNR下各算法BER曲线对比图

表2 不同SNR下和K的对比

图7 不同SNR下和K对比图

3.4 复杂度分析

表3 OMP和SADOMP算法运行时间对比

4 结束语

本文研究了OFDM系统信道估计问题，提出了一种基于CS的SADOMP算法。该算法利用DFT估计算法进行降噪处理，并将估计得到的信道频域响应用于CS算法残差的判断条件，使用Dice系数准则来度量残差向量与传感矩阵原子的相似度，实现了稀疏信号的快速准确重建。仿真结果表明，本文所提算法比传统的CS估计算法频谱利用率更高，并且有更好的NMSE和BER性能。同时，算法能够在稀疏度未知的情况下对稀疏度做出较为准确的估计。