高增益耦合电感有源钳位二次型DC-DC变换器

荣德生，刘谨瑞，孙瑄瑨，田东豪

(辽宁工程技术大学电气与控制工程学院，辽宁 葫芦岛 125105)

1 引言

随着新能源发电技术的推广，作为新能源发电系统的核心部件DC-DC变换器得到迅速发展[1-3]。为获取较低的电压应力、较高的电压增益和效率，学者们研究出了级联型变换器[4]、开关电容或开关电感型变换器[5,6]、交错并联型变换器等[7]，这些变换器都在某些方面有效地实现了上述目标。如文献[8]提出了耦合电感Boost变换器，电压应力有所降低，缓解了输出二极管的反向恢复问题，但不适用于大功率场合。文献[9,10]通过Boost变换器和电感倍压单元相结合，有效提高了电压增益，但因漏感的存在未能将电压增益最大化。文献[11]提出了带扩展倍压单元的钳位电路变换器，但输出二极管电压应力等于输出电压。文献[12]通过钳位电容吸收漏感能量，开关管的电压尖峰得到有效抑制，但输出二极管的电压应力仍有降低空间。文献[13]在传统有源钳位电路上进行改进，降低了二极管的电压应力，并且抑制了占空比丢失的现象，提升了变换器的性能。文献[14]使用有源钳位零电压导通(Zero Voltage Switch，ZVS)软开关技术，可以在电流连续的情况下实现软开关，并且易于控制，但并未明显提高电压增益。文献[15]将钳位支路分别钳位于输入端、输出端与地，经分析与实验证明钳位于地的电流纹波最小，提升了变换器的效率。文献[16]提出了一种二次型变换器，使电压增益与占空比成二次方关系，实现了高增益，但是电压应力也成倍增加，减少了适用场合。文献[17]在文献[16]的基础上，引入耦合电感单元，在输出端采用叠加电容的形式，进一步提高电压增益，而且采用无源支路吸收漏感能量，使得变换器效率有所提高，但所用元器件较多，电路较复杂。

本文受文献[10-13,16]的启发，提出具有有源钳位电路的耦合电感二次型DC-DC变换器。将耦合电感引入现有二次型Boost变换器中，总结出一类基于耦合电感的有源钳位Boost变换器。该类变换器通过耦合电感和钳位支路的有机结合，不仅提高了电压增益、有效地降低开关管的电压应力，而且利用有源钳位支路回收漏感能量，缓解了漏感与寄生电容谐振的现象，有效地抑制了开关导通时的尖峰电压，实现软开关工作状态。

2 组合式耦合电感二次型Boost变换器的提出

本文在二次型Boost变换器的基础上，增加自举电容，在自举电容支路中增加耦合电感，如图1右侧虚线所示，形成了LCVD支路。

图1 二次型变换器增加耦合电感电容支路

由于二次型Boost变换器结构的特殊性，当开关管S开通，电容C1可充当电压源，而LCVD支路在开关管S开通模态下进行储能，故二极管VD3中的阳极节点③便可连接至节点①和节点②。而对于耦合电感副边来说，可以与电感L1、L2进行耦合，故可组合成为四种具有耦合电感电容支路的二次型变换器，如图2所示，属于这一类的四种变换器均可以引入有源钳位电路实现高增益。

图2 四种耦合电感二次型变换器

根据二次型变换器的工作原理，当开关管S导通，电感L1由电源Vi储能，电感L2由电容C1储能。由于

(1)

故变换器4具有最大的电压增益。

3 工作原理分析

为进一步论证理论的正确性，本文采用图2中的变换器4进行拓扑分析，电路模型如图3所示。

图3 具有有源钳位的耦合电感二次型变换器

L1作为输入电感，钳位管Sc、反并联二极管VDc和电容Cc构成钳位支路，VD3和C2串联为副边充电构成回路。在分析之前假设：①所有元器件均是理想元器件，不考虑寄生参数影响；②电容足够大，其电压纹波可忽略；③励磁电感Lm足够大，励磁电流iLm连续，耦合电感的匝比为N。

在一个开关周期内，变换器存在8种工作模态，工作波形如图4所示，等效电路如图5所示。

图4 变换器的主要工作波形

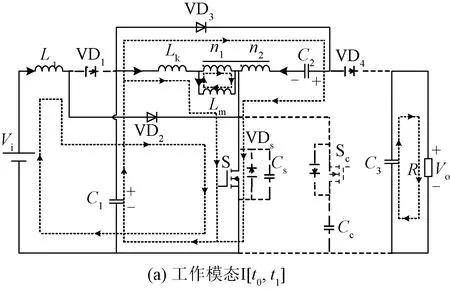
图5 各工作模态的等效电路

(1)工作模态I[t0，t1]：此模态下，开关管S、二极管VD2、VD3导通，VD1、VD4因承受反向电压而关断。电感L1由电源经二极管VD2和开关管S储能，其电流线性上升；漏感电流iLk和励磁电感电流在电容C1的作用下线性上升，由于漏感Lk远小于励磁电感，iLk的增速快于iLm。此时，处于正激状态的耦合电感与电容C1一起将能量传递到倍压电容C2上。此时，励磁电感和漏感电流的表达式为：

(2)

(3)

式中，k为耦合电感的耦合系数；ILm(t0)和ILk(t0)分别为iLm和iLk在t0时刻的值。

(2)工作模态II[t1，t2]：此模态下，开关管S，二极管VD1、VD4关断。由于寄生电容Cs的存在，开关管S在零电压状态下关断，电容Cs经由电感L1和二极管VD2开始充电。电容C1继续向耦合电感提供能量，负载由C3提供能量。因为Cs较小，所以此模态持续时间很短，故认为漏感电流和励磁电感电流近似不变。

(4)

式中，us(t)为t1～t2时刻开关管S的电压。

(3)工作模态III[t2，t3]：此模态下，二极管VD1、VD3以及钳位管Sc的体二极管VDc导通，二极管VD2、VD4因承受反向电压而关断。VDc两端电压被钳位到零，使得Sc可以零电压开通。电容Cc通过VDc吸收漏感能量，缓解了漏感与寄生电容谐振的现象，漏感电流开始下降，负载继续由电容C3提供能量。

(5)

(6)

(4)工作模态IV[t3，t4]：此模态下，二极管VD1、VD4导通。电源给电容C1充电，当电容C2和Cc的电压之和大于输出电压时，二极管VD4导通。存储在耦合电感和电容C2的能量经由二极管VD4开始向负载传输，VD3因承受反向电压而关断。漏感的存在使VDc继续导通，但流过VDc的电流会在电容Cc的作用下逐渐变小。当VDc为零时，Sc零电压开通。

(7)

(8)

(5)工作模态V[t4，t5]：此模态下，钳位管Sc导通，电源和电感L1给电容C1充电，电容Cc中存储的漏感能量经由二极管VD4向负载传输。漏感和励磁电感电流均线性下降，t5时刻，钳位管Sc关断。

(9)

(10)

(11)

(6)工作模态VI[t5，t6]：此模态下，钳位管Sc关断，VD1、VD4导通。Sc因电容Cc而零电压关断。电容Cs经由VD4放电，由于Cs较小，此模态持续时间很短，当Cs电压下降为零时，开关管S的体二极管导通，此模态结束。

(7)工作模态VII[t6，t7]：此模态下，电容C1继续由电源充电，开关管S的体二极管VDs导通，其电压被钳位到零，为开关管的零电压开通创造条件。此时电感L1、耦合电感与电容C2继续经由VD4向负载供能。在t7时刻，主开关零电压开通。

(12)

(13)

(8)工作模态VIII[t7，t8]：此模态下，开关管S导通。电容C1充电完毕，开始为耦合电感提供能量，所以二极管VD1因承受反向电压而关断；电感L1开始储能，二极管VD2自然导通。t8时刻，电容C2放电完毕，二极管VD3导通，输出二极管VD4关断，变换器进入下一周期工作。

(14)

(15)

4 变换器性能分析

4.1 电压增益

假设耦合电感的匝数比相同且为N，则N可以表示为：

(16)

假设耦合电感的耦合系数为k，耦合系数k可以表示为：

(17)

当变换器工作在模态I时，根据图5(a)，有：

VL1=Vi

(18)

VLm=kVC1

(19)

VC2=(1+Nk)VC1

(20)

当变换器工作在模态V时，根据图5(e)，有：

VL1=VC1-Vi

(21)

VLm=k(VCc-VC1)

(22)

VC2+NkVC1+VCc=Vo

(23)

根据输入电感L1的伏秒平衡原理，有：

(24)

根据式(21)，结合式(16)、式(19)得到电容C1电压的表达式为：

(25)

根据励磁电感的伏秒平衡，有：

(26)

根据式(23)，结合式(17)、式(20)得到电容Cc电压的表达式为：

(27)

结合式(18)、式(22)、式(24)、式(25)可以得到变换器的电压增益为：

(28)

根据式(28)可知，变换器的实际增益与上述变量有关。在实际应用中，耦合电感参数对变换器性能有一定的影响。

变换器电压增益与各参数的关系曲线如图6所示。当占空比一定时，耦合电感匝比N与电压增益成正比，与漏感成反比。故在实际应用设计中，耦合电感应尽量紧密耦合。

图6 不同变量下电压增益之间的关系曲线

4.2 元器件电压电流分析

为简化分析，将所有元器件均看做理想元器件，取耦合系数k=1，忽略漏感，此时变换器的电压增益为：

(29)

开关管S和Sc的电压应力为：

(30)

二极管VD1和VD2的电压应力为：

(31)

(32)

二极管VD3和VD4的电压应力为：

(33)

(34)

根据变换器工作原理，输入电感L1和励磁电感Lm的电流纹波表示如下：

(35)

(36)

式中，TS为开关管S一个周期的导通时间。

根据安秒平衡原理，得到各元器件电流如下：

(37)

(38)

(39)

(40)

4.3 软开关条件

电容Cs的存在降低了开关管和钳位管的关断损耗。当钳位管的反并联二极管导通，并且向钳位管施加关断信号来实现钳位管的ZVS导通。当钳位管断开时，漏感向开关管提供一个反向电流，Cs开始释放电荷。若漏感中的能量大于Cs中的能量，则开关管的电压在开通之前可降为零，从而实现ZVS导通，即：

LkILk(t6)2≥CsVs(t6)2

(41)

式中，ILk(t6)为t6时刻的漏感电流；Vs(t6)为t6时刻电容Cs的电压。

4.4 变换器性能对比

将本文所提变换器与文献[8,12,17]所提出的变换器的各项性能进行对比，结果见表1，其中，Vs-stress为开关管S所承受的电压。在匝比N固定的情况下，假设耦合电感的匝比N=1，变换器的增益对比曲线如图7所示，可以看出，本文所提变换器在不同占空比下均能获得良好的电压增益。

表1 变换器性能对比

图7 变换器增益对比曲线

5 实验结果与分析

本文制作了一台额定功率为150 W的样机，为验证上述分析的正确性，元器件参数见表2。

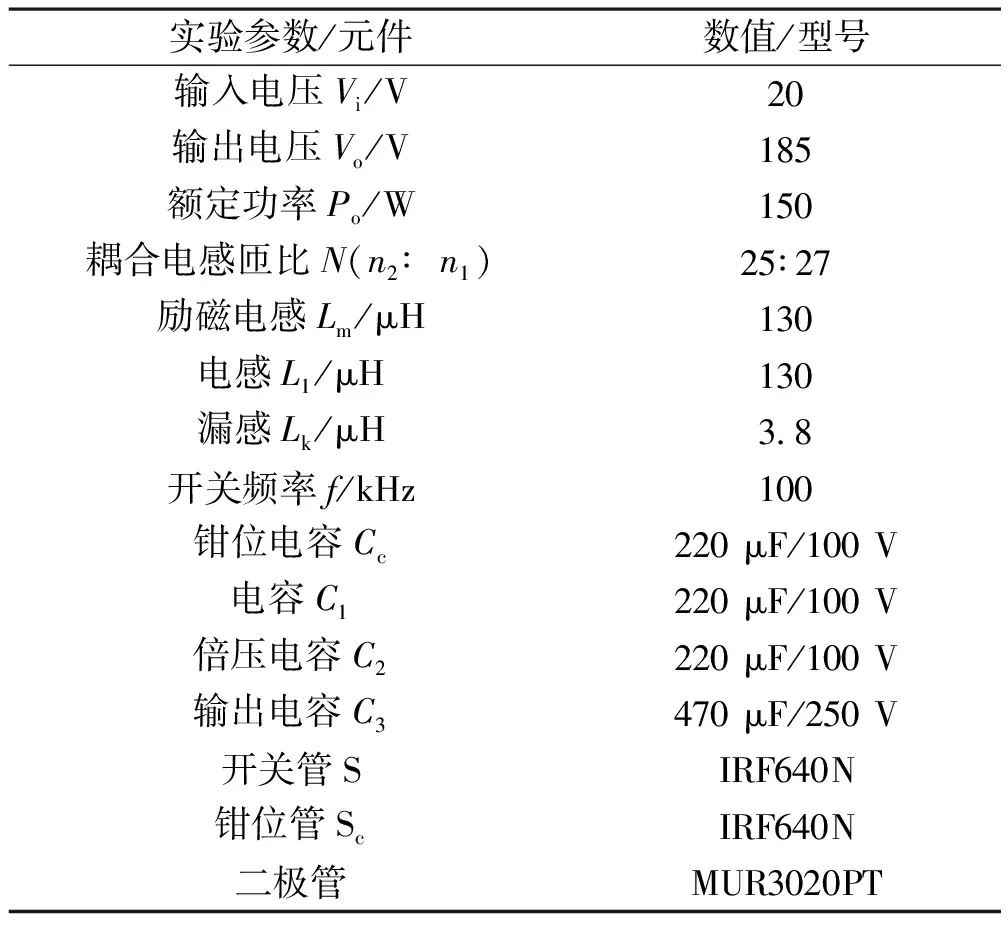
表2 元器件参数表

Vi、Vo波形如图8所示，可以看出，当占空比D为0.5、输入电压20 V时，变换器实际输出电压达到了185 V，由式(28)可知，受漏感和耦合电感匝比的影响，变换器的实际增益稍低于理论值。

图8 Vi、Vo波形

开关管S、Sc电压波形如图9所示，在输出电压为185 V的情况下，开关管的电压约为75 V，具有较低的电压应力，并且开关管可以实现零电压开通和关断，减小了开关管的损耗，提升了变换器的效率。

图9 开关管S、Sc电压波形

图10为电感L1和漏感的电流波形。可以看出，漏感电流在一个周期内下降到零，抑制了电压尖峰的产生，说明漏感能量得到了有效吸收，钳位支路的引入取得了良好的效果。

图10 电感L1与漏感Lk的电流波形

图11～图14为二极管VD1、VD2、VD3、VD4的电压、电流波形图。可以看出，二极管VD1、VD2、VD3可实现零电流关断，同时二极管的反向恢复电流几乎为零，抑制了二极管的反向恢复，并且二极管的电压均低于输出电压。图15为变换器效率随输出功率变化的曲线，最大效率达92.7%，当变换器在额定功率下(150 W)时效率达到92.1%。

图11 二极管VD1的电流、电压波形

图12 二极管VD2的电流、电压波形

图13 二极管VD3的电流、电压波形

图14 二极管VD4的电流、电压波形

图15 变换器效率曲线

6 结论

本文将耦合电感二次型高增益DC-DC变换器与有源钳位支路相结合，给出了变换器的各项性能，通过实验证明了理论分析的正确性。本文所提变换器具有如下特点：

(1)变换器可以通过调节占空比和耦合电感匝数比灵活调节输出电压，开关管的电压仅为输出电压的40%，可以选取耐压值低的开关管。

(2)有源钳位支路有效地回收了漏感中的能量并将其充分利用，抑制了电压尖峰，开关管可以工作在软开关状态，减小了变换器损耗。

(3)各二极管的电压应力为输出电压的20%～75%，可以选取低耐压值的二极管，缓解了二极管反向恢复的问题。通过理论分析和实验表明所提变换器适用于新能源光伏发电等领域。