基于振动时频信号灰度共生矩阵的有载分接开关触头状态检测方法研究

高树国，王丽丽，田 源，何瑞东，赵海涛，伊晓宇，李小玉，左浩明，张 凡

(1.国网河北省电力有限公司电力科学研究院，河北 石家庄 050000；2.国网河北省电力有限公司，河北 石家庄 050000；3.河北西柏坡发电有限责任公司，河北 石家庄 050000；4.西安交通大学电气工程学院，陕西 西安 710049)

1 引言

变压器有载分接开关(On-Load Tap Changer，OLTC)与调压线圈相连，在变压器处于负载状态下动态切换线圈匝数，实现了变压器电压的动态调节[1]。作为电力变压器中唯一的运动部件，分接开关在工作过程中承受显著的机、电、热应力，具有较高的故障率。国际大电网会议统计结果显示：30%的变压器故障来自于分接开关[2]。我国2005年变压器事故统计结果显示：分接开关引起的变压器故障比例约为27.8%[3]。因此对有载分接开关状态进行状态检测具有重要意义。

有载分接开关的故障类型主要有：零部件的变形或过度磨损、紧固件的松脱、运动的卡滞、超越终端位置、驱动机构和二次回路故障。研究人员相应地提出了转动力矩、电机电流、触头动作顺序监测等。由于有载分接开关在切换时，电机、连杆、齿轮箱、快速机构、触头等零部件会进行一系列的机械运动并引起振动。而这些振动与声音信号中包含上述部件的机械和运动状态，因而被广泛用于分接开关状态监测[4-6]。P.Kang采用连续小波变换计算奇异指数的方法，确定有载分接开关的振动信号跃变点[7]；他还利用所提取的小波特征量和自我迭代的方法计算连续小波变换的系数[8]；E.Rivas建立了母小波与分接开关振动信号的匹配机制，利用量化出的参数确定契合度最高的母小波，从而提高了利用小波变换处理有载分接开关振动信号的精准度[9,10]。不同于小波变换，希尔伯特变换能够绘制信号的包络线，对数据进行降维。汲胜昌等人利用了希尔伯特变换提取有载分接开关振动信号的包络，并利用奇异指数提取包络峰值[11]。段若晨等人提出在算法中添加掩模系数、利用窄带噪声对希尔伯特-黄变换进行了改进，克服了模态混叠的缺点[12,13]。此外，樊家昊等人提出了利用递归法分析分接开关切换过程中的振动信号[14]；潘志城等人提出了时频域振动特征的真空有载分接开关状态检测方法[15]；马宏忠等人提出一种基于改进排列熵和K-means的分接开关机械故障诊断方法，并对触头松动、弹簧性能下降等缺陷进行了研究[16]；宋东东提出了燃弧损耗模型及在线监测方法[17]；赵寿生利用经验模态分解(Empirical Mode Decomposition,EMD)算法对有载分接开关的振动信号进行去噪[18]；张杰等人采用独立成分分析(Independent Component Analysis,ICA)对混合信号进行了分离，并以分接开关各机械状态下的相空间分布系数为基础，建立正态型隶属度函数，对触头松动、掉落、磨损等机械状态进行识别[19]；杨森等人利用变分模态分解对有载分接开关振动信号进行去噪分析[20]。

从上述研究现状可知，目前对紧固件松动的故障机理和识别方法已经较为成熟，但还缺少对触头缺陷故障的模拟实验和诊断。在长期使用中，分接开关触头长期承受电弧和碰撞容易出现磨损和烧蚀，因而对上述两种故障类型的诊断具有非常重要的意义和应用价值。本文搭建了M型分接开关的实验平台，对切换过程中的振动信号进行了小波时频分析，构建时频信号的灰度共生矩阵，计算灰度共生矩阵的能量标准差；最后对有载分接开关静触头磨损、烧蚀进行实验模拟，获得不同缺陷程度下能量标准差的变化规律。本文的研究内容可为基于振动信号的分接开关机械状态检测技术提供基础。

2 分接开关工作原理及油室桶固有振动特性

2.1 M型分接工作原理

M型有载分接开关，因其切换芯子一个扇区内的动静触头在圆周方向呈现M型而得名，普遍应用于电压等级220 kV以下、容量150 MV·A以下的主变压器。它由切换开关、切换开关油室和分接选择器(带极性转换开关)组成，如图1所示。分接选择器选择变压器调压绕组抽头，切换开关完成对分接位置的切换。分接选择器以及切换开关通过机械连轴配合进行切换。切换开关内部各个触头结构如图2所示。

图1 M型有载分接开关结构

图2 切换开关内部的触头结构

其中MCa和MCb为主触头，MSCa和MSCb为主通断触头，TCa1和TCb1为过渡触头。正常工作时，MC和MSC触头均接入回路，由于MSC回路电阻大于MC，此时电流主要流经主触头MC。快速机构过死点释放后，主触头、主通断触头和过渡触头依次断开与闭合。触头间碰撞产生一系列振动冲击信号，经固体连接和变压器油传递至油箱表面。因此，可以利用振动信号对分接开关的状态进行诊断。

2.2 实验平台

利用贵州长征公司1987年生产的一台M型分接开关搭建实验平台，分接开关参数见表1。将开关及其电动机构安装在支撑架上简易模拟有载分接开关在变压器中的安装状态，如图3所示。

表1 分接开关参数

图3 M型有载分接开关实验平台

选用压电式振动加速度传感器PCB 603C01、24位同步数据采集卡组建分接开关振动信号采集装置，传感器参数见表2。振动加速度传感器安装在环氧树脂筒表面，距触头较近的位置处。

表2 振动加速度传感器参数

2.3 分接开关固有振动特性

切换开关内部动静触头闭合时产生的碰撞可视为对分接开关整体的一系列冲击激励，因而触头表面状态的变化会改变系统的固有振动特性，最终引起振动信号的改变。采用力锤激励、加速度传感器拾振的方式同步采集激励和响应信号，从而获得分接开关的冲击振动响应信号。实验获得切换开关内部充油和不充油条件下分接开关整体的振动幅频响应特性如图4所示。

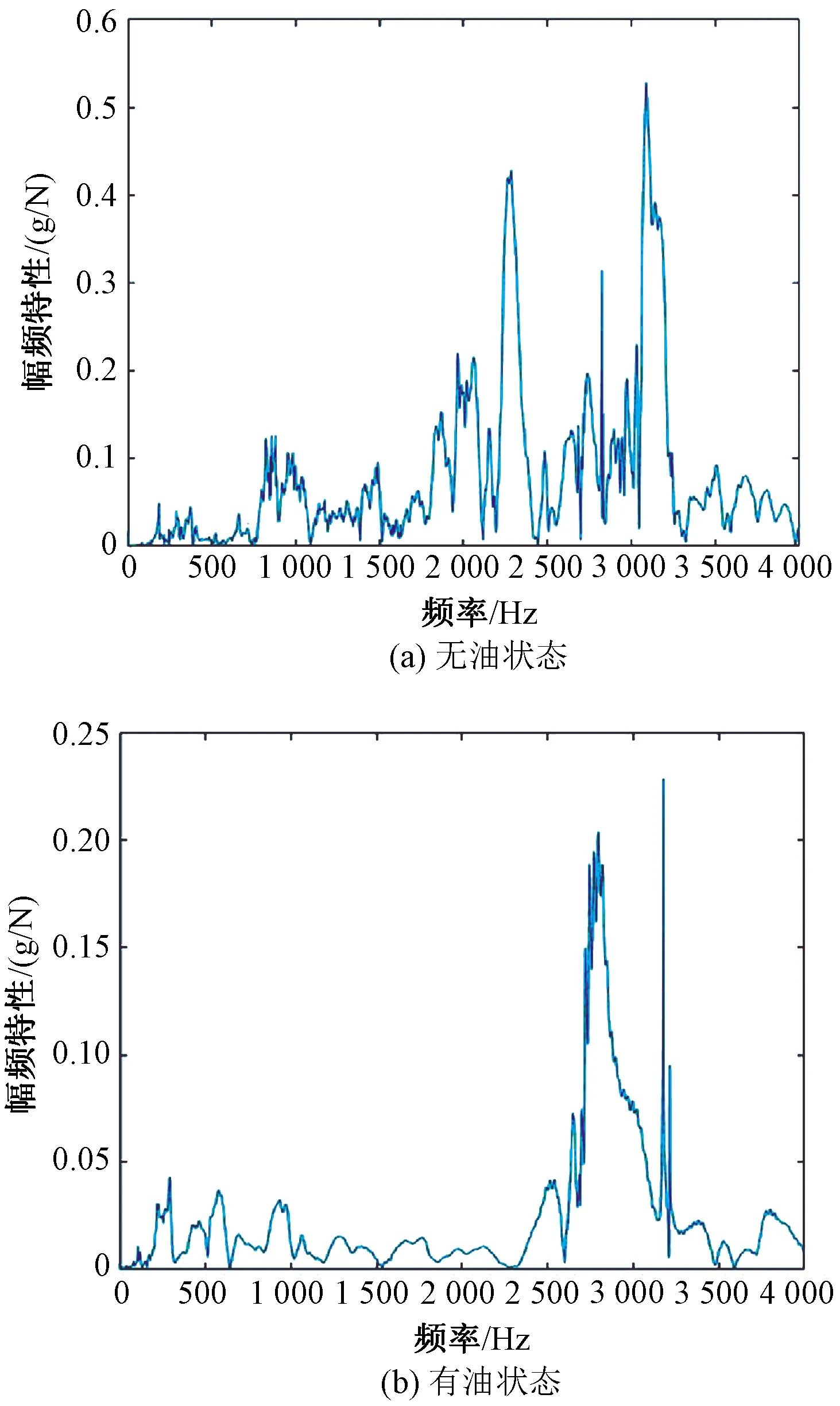
图4 切换开关油室充油前后的振动响应

由实验结果可知，油室充油后，振动响应的幅值降低，谐振峰的数量减少，曲线低频部分变得更为光滑。上述现象可以解释为：油室浸油后，变压器油的质量阻尼效应加载在切换开关筒壁上，使得系统的固有频率降低，阻尼比增大，因而曲线谐振峰向低频移动，曲线变得光滑。此外，充油后的分接开关在2 500～3 500 Hz的振动响应具有较高幅值，说明该频段内的信号具有较高的信噪比，适宜利用该频段内振动特征的变化提取特征值。

3 基于时频信号灰度共生矩阵的故障诊断方法

3.1 传动装置和开关振动信号分离方法

有载调压开关切换时，异步电机转动并通过轴和齿传动，因此采集到的振动信号同时包含了开关本身以及传动装置的振动。齿轮磨损的驱动机构信号中存在高频振动信号，容易与分接选择器和切换开关的振动信号混叠，因此需要从混合振动信号中分离获得分接开关的振动。

假设混合信号满足线性叠加条件，且电动机构振动信号具有一定的时序特点，可以表示为：

X(t)=AS(t)

(1)

Y(t)=WX(t)

(2)

式中，S(t)为混合前的原始信号；X(t)为测得的混合信号；Y(t)为由分离算法获得的原始信号；A、W分别为信号混合矩阵与分离矩阵。

利用二阶盲辨识算法(Second Order Blind Identification, SOBI)对混合信号进行分离。该算法的具体步骤如下：

(1)针对采集到的混合信号利用白化矩阵V进行白化的预处理，使Z(t)的协方差矩阵为单位阵，获得白化后的矩阵为：

Z(t)=VX(t)

(3)

(2)计算混合后信号协方差矩阵为：

RX(0)=E[X(t)XT(t)]=ARS(0)AT

(4)

(3)计算混合信号的延时相关矩阵为：

RX(τ)=E[X(t)XT(t+τ)]

(5)

令一系列互不相等的值τ1,τ2,τ3,…,τp为延时值，代入式(5)中可分别计算出一组延时相关矩阵RS(τi)。将其白化后进一步计算获得：

RZ(τi)=URS(τi)UT

(6)

式中，U=VA。

由于Z(t)能够保证各个向量元素是正交归一的，由此推论出矩阵U也必定能够满足正交归一条件，即能够将式(6)改写成：

RZ(τi)=UTRS(τi)U

(7)

(4)获得信号的解混矩阵W为：

W=UTV

(8)

分接开关正常工作时传动装置和开关本体的混合振动加速度信号如图5(a)所示。由图5(a)可知，从驱动电机起动至切换完成共持续约5 s。电机起动后，传动机构的振动幅值小于0.5g(g为重力加速度，1g=9.8 m/s2)，约1.5 s后出现第一个较大幅值的振动脉冲信号，对应分接选择器的分合，3～4 s之间存在若干个高幅值的脉冲信号，最大幅值约20g，来自快速机构的释放和切换开关中各个动静触头之间的碰撞。

利用上述SOBI分离算法针对有载分接开关中不同位置加速度传感器采集到的振动信号进行分离，分离的传动系统的振动信号如图5(b)所示。由图5(b)可知，混合信号分离后传动系统的幅值与分离前传动系统的电机振动幅值相近，在0.5g以内。原始信号中分接选择器和切换开关动作时产生的冲击振动信号的峰值显著减低。从分离前后的信号来看，该算法能够成功实现有载分接开关本体以及电动机构振动信号的分离。

图5 混合振动信号与分离后传动机构的振动信号

3.2 灰度共生矩阵能量值的时频特征提取方法

分接开关切换时的振动信号属于典型的时变非平稳信号，因此适宜采用信号的小波时频分析方法。小波变换利用小波作为基底，通过伸缩以及平移的累积来实现对信号的时频分析。设小波母函数为ψ(t)，则其在函数空间L2(R*)中满足式：

(9)

(10)

(11)

式中，函数ψ(a,b)(x)为由小波母函数ψ(t)生成的依赖于参数对(a,b)的连续小波函数；a为伸缩的比例；b为位移参数。

选择Harr小波对分接选择器闭合至切换开关结束切换时共3 s内的振动信号进行时频分析，结果如图6所示。由图6可知，切换开关引起的振动信号最为强烈，能量集中在0～4 000 Hz。

图6 分接开关振动信号的时频分析

灰度共生矩阵(Gray Level Co-occurrence Matrix, GLCM)能够反映时频信号的纹理特征，结合特征值可以用于分接开关状态的判断。按照以下步骤计算共生矩阵及特征值：

(1)将时频分析的幅值灰度化(即幅值变换到0～252范围内)。

(2)计算时频矩阵的灰度共生矩阵，该矩阵主要表示某一个点Δm和Δn位置灰度值为i和j的概率分布：

(12)

m2=m1+Δm

(13)

n2=n1+Δn

(14)

式中，i,j=1,2,…,L；〈〉代表矩阵中某个元素对(i,j)元素处产生的共生值；Δm和Δn分别为该元素到元素(i,j)需要左右以及上下移动的位移；f(x,y)为一幅二维数字图像的灰度，其大小为Lm×Ln，Lm以及Ln为像素空间位置，Lm=1,2,…,Nm,Ln=1,2,…,Nn；(m1,n1)为图像中一点的坐标；(m2,n2)为另一点坐标。

共生矩阵实际上是两个像素点的联合直方图，对于图像中细而规则的纹理，成对像素点的二维直方图倾向于均匀分布；对于粗而规则的纹理，则倾向于最对角分布。

(3)在计算I(i,j)的共生矩阵之后，还需要对其进行归一化处理。将共生矩阵的各个数值除以矩阵中的最大元素。

(4)计算不同档位切换过程中振动信号的时频域矩阵的GLCM，再根据频带计算获得对应的能量值。能量值的定义为：

(15)

能量变换反映了图像灰度分布均匀程度和纹理粗细度。若灰度共生矩阵的元素值相近，则能量较小，表示纹理细致；若其中一些元素值大，而其他值小，则能量值较大。能量值大表明一种较均匀的纹理模式。

(5)求得不同档位对应的能量值后，再计算切换过程不同档位对应的各个频带能量标准差平均值。

分接开关触头磨损和烧蚀故障后，触头质量和碰撞时的接触刚度发生变化，引起振动信号和GLCM能量值的改变，因此可以根据能量变化对分接开关故障进行诊断。

4 触头磨损和烧蚀缺陷对分接开关振动特性的影响

原切换开关的静触头及安装面板如图7所示，静触头表面进行了凹凸处理，从而减少动、静触头的接触电阻。为了获得触头磨损与烧蚀缺陷对应的振动信号，制作了多个表面平整、无凹凸的静触头。

图7 切换开关静触头

更换分接开关的触头后，进行1～19档和19～1档连续切换，采集各个档位切换过程中的振动信号。然后利用第3节中的SOBI算法从分接开关混叠振动信号分离获得分接选择器和切换开关的振动信号，再进行小波时频变换，提取切换过程的不同档位对应的各GLCM能量标准差的平均值。

4.1 触头磨损

原触头的厚度为8 mm，磨损故障为触头厚度的减少，因此分别加工了厚度为6 mm和4 mm的静触头。该分接开关为双断口结构，因此每套触头包括2对主通断触头，2对过渡触头，共计8个触头。不同厚度的静触头如图8所示，从左至右厚度分别为8 mm(原触头)，6 mm以及4 mm。

图8 不同厚度的静触头

实验获得触头不同磨损程度振动信号时频分析结果及GLCM能量标准差如图9所示。由图9可知，不同触头厚度对应的时频信号整体分布相似，但最大幅值存在明显差异。随着触头厚度的减小，时频图中的最大幅值逐渐减小。从GLCM能量标准差来看，低频段1～2 000 Hz能量没有明显的区别，但是2 000 Hz以上高频能量随厚度减小而增大。该现象可以解释为：静触头厚度减小，质量降低，触头碰撞系统的固有频率升高，因而2 000 Hz以上振动响应的能量明显增大。8 mm、6 mm和4 mm触头对应的能量标准差分别为0.037、0.04和0.042。

图9 触头不同厚度的时频振动信号及GLCM能量标准差

4.2 触头烧蚀

采用高温电弧的电焊工具，对触头表面进行烧蚀，从而获得不同烧蚀程度的静触头，如图10所示。由图10可知，烧蚀后的触头表面呈现黑褐色，出现多个电弧高温烧蚀的黑斑点，且能够观察到一部分表面出现了绿色的物质，即在电弧的作用下铜金属表面产生了一定的氧化物质。利用砂纸对除了与动触头接触的表面进行打磨，再将触头安装到固定板上。

图10 不同烧蚀程度的静触头

实验获得触头不同烧蚀程度振动信号时频分析结果及GLCM能量标准差如图11所示。由图11可知，不同触头厚度对应的时频信号整体分布相似，但最大幅值存在一定差异。由于电弧在触头表面产生多个凹凸不平的烧蚀坑，减小了静触头的刚度，动静触头碰撞过程中产生的高频信号能量降低。结合磨损和烧蚀对触头的影响可知，磨损引起触头质量降低，使得触头系统的固有频率升高，因而高频振动信号的能量标准差增大，而烧蚀引起触头接触刚度的降低使得固有频率降低，最终高频振动信号的能量标准差减小。两种缺陷具有相反的影响规律，但从实验结果来看，触头烧蚀对高频能量标准差的影响大于触头磨损。8 mm、6 mm和4 mm触头烧蚀条件下振动信号能量标准差分别为0.031、0.034和0.036。

图11 触头不同烧蚀程度对应的振动时频信号及GLCM能量标准差

5 结论

本文搭建了M型有载分接开关实验平台，在切换开关静触头上模拟了磨损和烧蚀两种故障，提取了振动时频信号灰度共生矩阵，并计算了不同触头状态对应的能量标准差。获得的主要结论有：

(1)分接开关切换过程中的振动信号包含了传动装置、分接选择器和切换开关的信号，采用二阶盲辨识算法可以有效地从混叠振动信号中分离出分接选择器和切换开关的振动信号。

(2)触头磨损后质量减小，接触碰撞时产生的高频能量标准差增大。厚度降低4 mm时对应的高频能量标准差增大约20%。

(3)触头烧蚀后表面出现多个不平整的烧蚀坑，使得触头表面的接触刚度降低。动静触头碰撞过程中产生的高频信号能量下降，4 mm、6 mm和8 mm触头烧蚀条件下振动信号能量标准差分别为0.036、0.034和0.031。

本文的研究内容揭示了触头磨损和烧蚀对切换过程振动信号的影响规律，振动信号时频分析结果GLCM标准差的变化，可为基于振动信号的有载分接开关状态评估提供基础。