捷联制导旋转弹制导信息提取研究

侯思林，杨 军，丁禹鑫

(西北工业大学航天学院，西安 710000)

0 引言

捷联式导引头与常规框架式导引头相比，具有体积小、可靠性高、视线角速率不受限制及成本低等优点，因此具有很大的应用前景，捷联制导技术也成为了国内外的研究热点。旋转弹与非旋转弹相比，具有系统结构简单、成本低、可靠性高等特点，其弹体的自旋运动能够克服诸如推力偏心、起控点散布、弹体质量分布不均匀等问题。因此，随着导弹小型化和精准化的发展，将捷联式导引头应用在旋转弹上有着广阔的发展前景。

在不同的应用背景下，国内外学者对导弹制导信息的提取技术做了大量的研究：H.Rotstein和J.Refiner等基于卡尔曼滤波器，对惯性导引头融合系统的可观测性进行了研究；J.Waldmann针对框架式图像模式导引头，利用线性反馈控制实现了与弹体姿态信息的解耦，采用扩展卡尔曼滤波(Extended Kalman Filter, EKF)实现了对导引信息即视线角速率的提取，并采用蒙特卡罗方法完成了仿真验证；S.A.Elgamel和J.Soraghan使用卡尔曼滤波器，设计了一种在干扰背景下的目标增强跟踪方法；J.Yun等基于无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)实现了对捷联导引头系统制导信息的估计；李憬憬等基于粒子滤波器完成了捷联导引头视线角速率的提取，并进行了仿真分析；庞威和谢晓方等基于滑翔制导炸弹的应用背景，利用一种改进粒子滤波完成了捷联导引头制导信息估计和半实物仿真验证，并与UKF和粒子滤波的估计结果进行了对比分析；李相平和陆志毅等基于自适应性卡尔曼滤波，对捷联相控阵雷达导引头的角速率解耦和估计进行了研究。

本文以捷联式半主动激光导引头为研究对象，并将其应用于旋转弹上研究制导信息的提取方法。捷联式半主动激光导引头测量弹目角度信息的工作原理是通过外部的激光发射器照射目标，导引头上的激光寻的器接收回波信号，从而得到弹目失调角信息。由于捷联式半主动激光导引头固连在弹体上，测得的弹目失调角信息耦合了弹体的姿态角信息，不能直接应用于旋转弹制导控制系统，因此需要解耦得到惯性坐标系下的视线角信息。基于解耦模型的非线性，本文采用EKF方法进行制导信息的估计，并与-滤波结果进行对比。EKF是一种比较常用的处理非线性问题的滤波算法，其主要思想是对非线性函数进行泰勒展开，仅保留一阶线性项,从而得到一个线性化近似模型，这种方法虽然会产生一定误差，但是因其计算量很小，在工程上应用十分广泛。

1 制导信息估计模型的建立

1.1 坐标系定义

为建立制导信息估计模型，首先定义以下坐标系：

(1)地面坐标系

地面坐标系与地球固联，原点取导弹质心在水平面上的投影点;轴在水平面内，指向目标为正；轴与地面垂直，向上为正；轴按右手定则确定。

(2)弹体坐标系

弹体坐标系与弹体固联，原点取在导弹的质心上；轴与弹体纵轴重合，指向头部为正；轴在弹体纵向对称平面内，垂直于轴，向上为正；轴垂直于平面，方向按右手定则确定。

(3)视线坐标系

视线坐标系定义为，原点取在导弹的质心上；轴与弹目视线重合，指向目标为正；轴在铅垂平面内，垂直于轴，向上为正；轴按右手定则确定。

(4)体视线坐标系

体视线坐标系定义为111，原点取在导弹的质心上；1轴与弹目视线重合，指向目标为正；1轴和轴根据2-3顺序的坐标旋转规则由弹体系来确定。

各坐标系之间的关系如图1所示。

图1 各坐标系之间的关系Fig.1 Relationship between coordinate systems

1.2 状态方程的建立

本文选用目标的位置和运动速度作为状态变量，建立系统的状态方程，具体如下：

假定目标做匀速直线运动，运动速度为，在时刻，设目标的位置为()，经过采样时间之后，目标的位置为(+1)=()+。显然，在地面坐标系中，目标在、、方向都有相应的分量，所以在目标运动过程中可表示为

(1)

将系统的状态量表示如下

(2)

则系统的状态方程表示为

+1=(+1,)+(+1,)()

(3)

式中，为时刻状态向量；(+1,)为状态转移矩阵；(+1,)为噪声矩阵；()为系统噪声向量，此处表示为对速度的扰动量。

其中

(4)

(5)

1.3 观测方程的建立

根据地面坐标系和视线坐标系的定义，目标在地面坐标系的位置关系可由弹目视线角表示为

(6)

根据弹体坐标系和体视线坐标系的定义，目标在弹体坐标系的位置关系可由捷连导引头输出的两通道失调角表示为

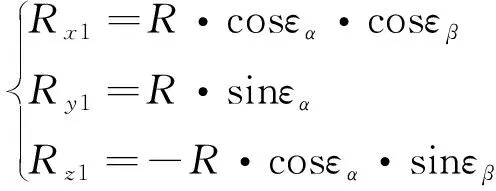
(7)

又因为牵连地面坐标系到弹体坐标系的变换矩阵为

(,ϑ,)=

(8)

所以可得

(9)

即

(10)

令

(11)

并将其代入式(10)可得

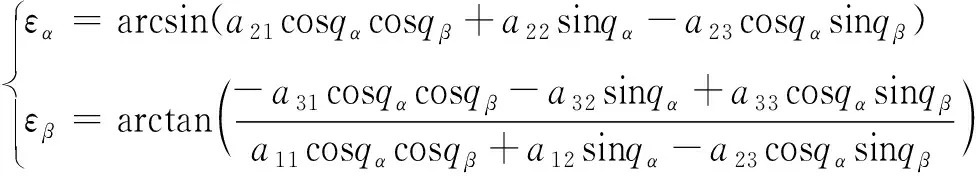
(12)

式中，和可用状态变量()、()、()表示为

(13)

式中，、、为导引头在地面坐标系的坐标分量。因此，可以得到离散的观测方程为

(14)

2 扩展卡尔曼滤波器设计

由于建立的制导信息提取模型中状态方程是线性的，观测方程是非线性的，所以只需要对观测方程进行线性化处理得到观测雅可比矩阵。

因此，根据建立的制导信息估计模型，设计扩展卡尔曼滤波器如下：

1)设定初始状态，初始协方差矩阵；

2)状态和观测的一步预测

(15)

3)求解观测方程的雅可比矩阵

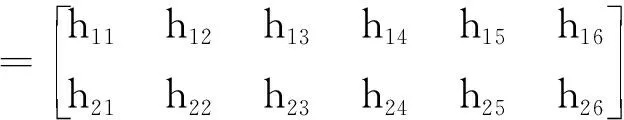
(16)

其中

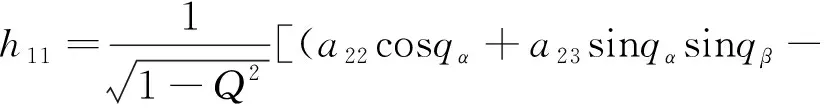
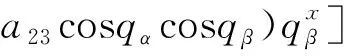
(17)

(18)

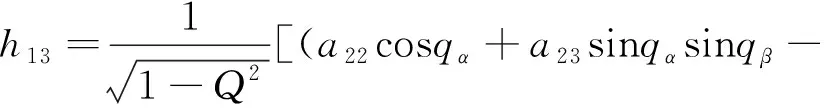
(19)

===0

(20)

(21)

(22)

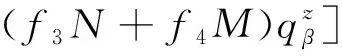
(23)

===0

(24)

式中

=coscos+sin-cossin

=-coscos-sin+cossin

=coscos+sin-cossin

=sincos-cos-sinsin

=sincos-cos-sinsin

=cossin+coscos

=cossin+coscos

(25)

(26)

(27)

(28)

(29)

式中

4)求一步误差方差矩阵预测

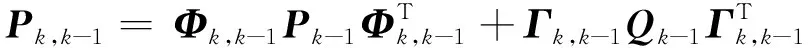
(30)

5)求卡尔曼增益

(31)

6)状态和方差更新

(32)

=(-),-1

(33)

通过以上扩展卡尔曼滤波器的设计，可以估计出惯性系下目标的位置(,,)，再根据导引头的空间位置便可以得到惯性系下的弹目视线角如下

(34)

最后对惯性系下的视线角进行微分处理，并加入一阶低通滤波器，可以得到视线角速度，如此便完成了制导信息的提取。

3 仿真验证

根据第2节设计的扩展卡尔曼滤波器，采用MATLAB进行捷联制导旋转弹制导信息提取的仿真验证。本次仿真考虑捷联式半主动激光导引头的测量噪声特性、目标位置初始测量误差以及旋转弹速率陀螺仪的测量特性。具体仿真条件如下：

捷联式半主动激光导引头的输出频率为50Hz，给定导引头的测量误差为均值为0、均方差为0.1°的离散白噪声；目标在地面坐标系的实际位置为(5000,0,0)m，目标位置初始测量误差为(50,50,50)m，因此导弹发射前装定的目标位置为(5050,50,50)m；假定旋转弹的初始位置为(0,1000,0)m，沿水平方向飞行，速度为600m/s，目标静止；旋转弹的俯仰角和偏航角的扰动量为幅值2°、频率3Hz的正弦变化，滚转角速度为10rad/s，考虑速率陀螺仪的测量零位为0.05(°)/s，测量噪声为均值为0、均方差为0.3°的离散白噪声，速率陀螺的采样频率为200Hz。

采用EKF方法和-滤波方法的仿真结果如图2～图5所示。

图2 视线高低角变化图Fig.2 LOS pitch angle variation diagram

仿真结果给出了采用EKF和-滤波时视线角和视线角速率的滤波值，表1给出了收敛后滤波值与真实值的均方根误差。从仿真结果可以看出，本文设计的EKF的滤波误差小于-滤波，旋转弹制导信息的估计精度更高，且EKF的收敛速度更快。

图3 视线方位角变化图Fig.3 LOS azimuth angle variation diagram

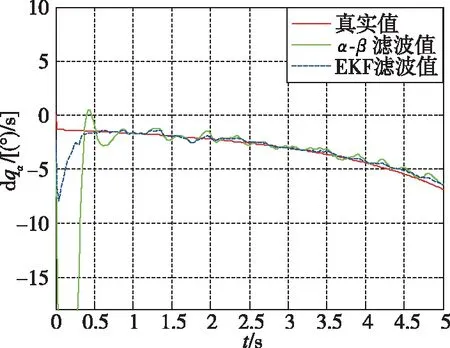
图4 视线高低角速率变化图Fig.4 Diagram of LOS pitch angular rate

图5 视线方位角速率变化图Fig.5 LOS azimuth angular rate variation diagram

表1 EKF和α-β滤波值与真实值的均方根误差

4 结论

本文以捷联式半主动激光导引头为研究对象，设计了捷联制导旋转弹制导信息的提取方法。首先，以目标的位置和速度为状态变量建立了状态方程，以导引头的测量值为观测量建立了观测方程，得到了制导信息的解耦模型。然后，针对观测方程的非线性问题设计了扩展卡尔曼滤波器，对目标的位置信息进行估计，根据弹目位置关系估计出视线角和视线角速率。最后，针对导引头和速率陀螺仪的测量特性进行了EKF方法的仿真验证，并与-滤波结果进行了对比，最后得出了本文设计的EKF算法对旋转弹制导信息的估计精度更高，收敛更快。本文的研究结果为捷联式半主动激光导引头在旋转弹上的应用提供了参考。