水下复杂环境下基于SINS/USBL/DVL 多源信息融合的组合导航算法

王 健，鲁金瑞，郑 栋，李 璇，张 涛

(1. 北京控制与电子技术研究所，北京 100038；2.火箭军装备部驻北京地区第七军事代表室，北京 100039；3. 东南大学仪器科学与工程学院，南京 210096)

0 引言

目前已有的水下定位技术包括捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)、声学导航、地球物理场导航及其水下组合导航等。地球物理场导航利用地球的物理场信息进行定位，主要包括地形匹配、地磁匹配和重力匹配等，但需要事先获得活动区域的海图作为匹配的数据库，测绘工作量较大，测试设备昂贵且随维数增加匹配计算的复杂度增大。声学导航包括水声定位系统和多普勒测速仪(Doppler Velocity Log，DVL)两类。DVL是基于多普勒效应的测速设备，能测得载体相对于海底和水流的速度且误差不随时间累积。由于声波在水下传输距离远、衰减损失小，因而水声定位技术得到了充分发展，超短基线(Ultra Short Baseline，USBL)成为水声定位设备发展的热点。目前，常用的水下组合导航方式有SINS/DVL组合和SINS/USBL组合导航。但是，SINS/DVL组合导航虽然能够获得高精度的速度信息，但位置误差随时间是发散的；SINS/USBL组合导航虽然能够抑制位置误差的发散，但受换能器作用距离的限制，常用于区域内的高精度定位，无法满足水下航行器长航时、广区域内导航与定位的需求。其中，北京自动化控制设备研究所张亚文提出了一种基于集中滤波的SINS/DVL/USBL水下组合导航方法，建立了杆臂在线估计的SINS/DVL速度观测模型和SINS/USBL相对量测信息的观测模型；哈尔滨工程大学徐博和赵琳等推导了SINS/USBL组合的子滤波器，结合SINS/DVL子滤波器，提出了SINS/USBL/DVL组合的分布式联邦滤波，具有较高的容错性和稳定性。但是，目前公开的研究大多数还处于仿真和半物理验证阶段，还需要经过实际长江或海试试验来充分验证，在试验中发现问题并解决问题的工作还未全面展开。同时，海洋空间物理特性复杂导致水声传播信道表现为时变、空变和频变等不确定，海洋环境噪声，特别是浅海环境噪声具有噪声源复杂、统计分布多样、声源多变等特征。因此，水下复杂声场环境所导致的声学量测信息的不确定性也会影响导航的性能。

因此，为了实现水下航行器在复杂水下声场环境下高精度、长航时的导航与定位，本文对基于SINS/USBL/DVL多源信息融合的组合导航算法展开研究，旨在提高水下组合导航的精度、鲁棒性和可靠性。

1 SINS/USBL/DVL多源融合的滤波模型

1.1 SINS/USBL相对量测信息组合的滤波模型

区别于传统位置匹配的SINS/USBL组合定位技术，本节提出了基于相对量测信息的SINS/USBL组合导航策略。SINS/USBL组合导航系统的状态变量，在SINS的15维状态量的基础上加入了USBL状态误差量，相应SINS状态变量选择为

=[δδδδδ

(1)

SINS的状态方程为

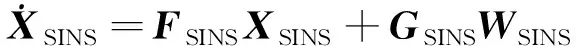
(2)

将SINS/USBL一体化安装误差角δ=[δδδ]和测角误差δ、δ、USBL测距精度误差δ设置为状态变量，则USBL的状态变量选择为

=[δδδδδδ]

(3)

定义δ=[δδδ]，由于安装误差角、测角误差和 USBL 测距精度误差等均为小量，可以视为常数，USBL的状态方程为

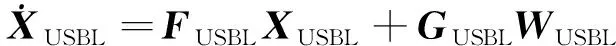
(4)

其中，=，则SINS/USBL一体化组合导航系统误差状态变量为

=[]

(5)

SINS/USBL组合系统的状态误差方程为

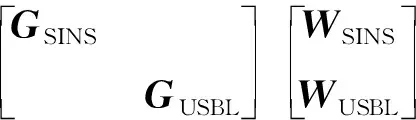
(6)

定义USBL直接输出的量测信息为[

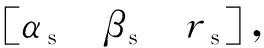
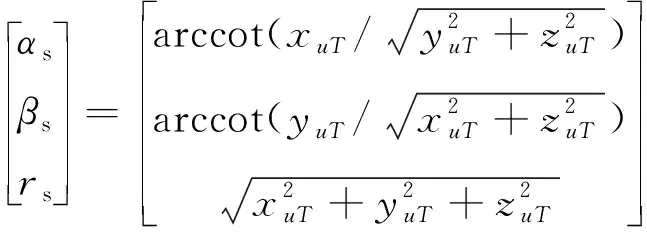
(7)

对式(7)求偏微分可得

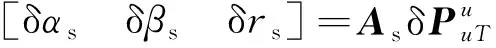
(8)

其中

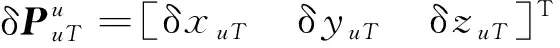
(9)

(10)

(11)

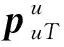
(12)

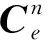
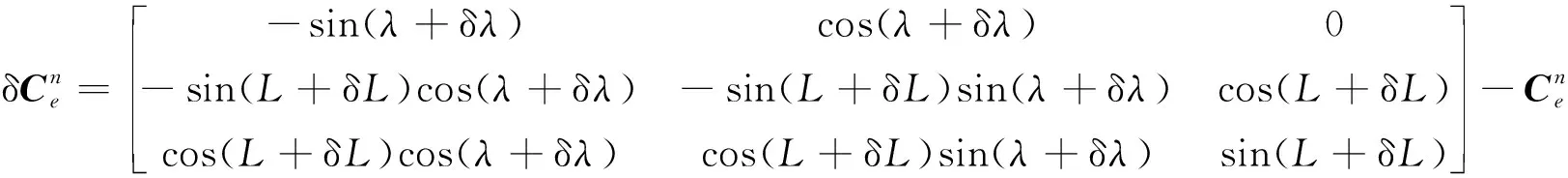
(13)

(14)

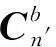
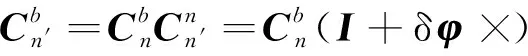
(15)

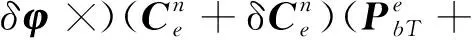
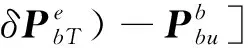
(16)

忽略式(16)的高阶误差小量，则

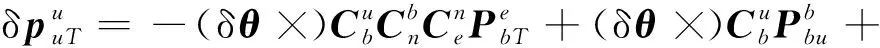
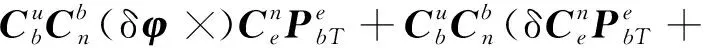
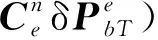
(17)

其中，根据反对称矩阵具有交换性，则

(18)

根据式(16)，则

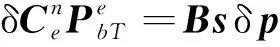
(19)

(20)

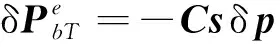
(21)

=

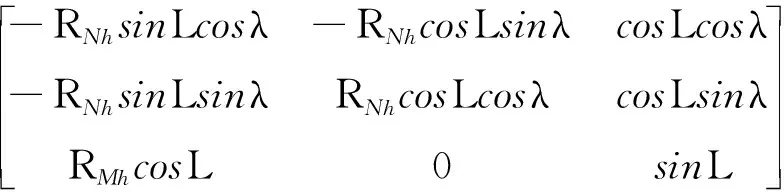
(22)

将式(18)～式(22)代入式(17)，进一步整理为

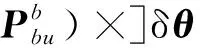
(23)

将式(23)代入式(8)，解算出应答器相对SINS投影于-系的方位角和斜距为

(24)

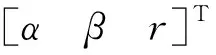
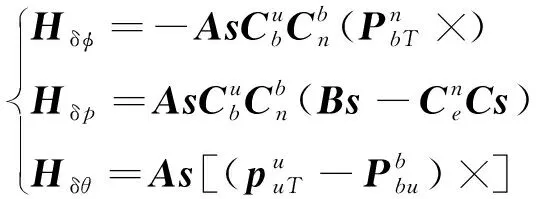
(25)

USBL观测到的方位角和斜距可表示为

(26)

将式(24)与式(26)相减得

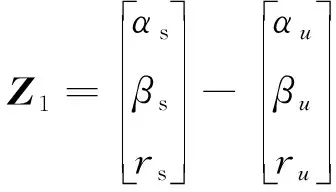
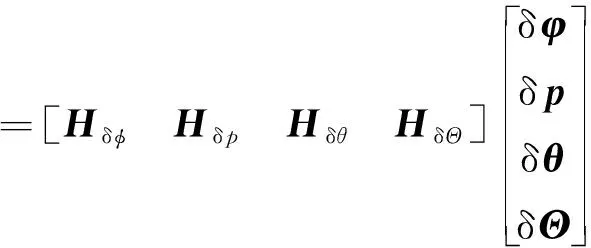
(27)

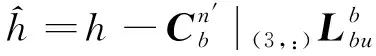
(28)

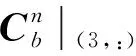
=0+Δ

(29)

其中，Δ为观测噪声，式(28)和式(29)相减得到深度误差观测量

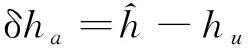
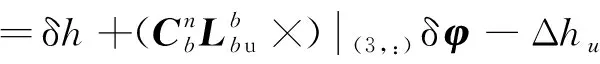
(30)

则观测方程表示为

=δ+δδ-Δ

(31)

SINS/USBL一体化组合系统滤波的量测方程可表示为

(32)

观测矩阵为

(33)

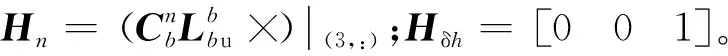
观测噪声阵为

(34)

1.2 SINS/DVL基于载体坐标系下速度组合的滤波模型

根据文献[5]的推导，本节给出了SINS/DVL基于载体坐标系下速度组合的滤波模型。SINS/DVL组合导航系统误差状态变量为

=[]

(35)

其中，=[δ]，δ是DVL的刻度因子误差，量测方程可表示为

=+

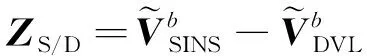
(36)

观测矩阵为

(37)

1.3 SINS/USBL/DVL多源信息融合的集中滤波模型

综上所述，进一步结合集中滤波的特点，SINS/USBL/DVL组合导航集中滤波的状态方程为

(38)

其中，状态变量为

(39)

系统矩阵可以表示为

(40)

其中，和为滤波器相关噪声矩阵项，SINS/USBL/DVL组合导航集中滤波的观测方程为

=+

(41)

2 量测不确定下SINS/USBL/DVL多源融合的鲁棒自适应滤波算法

在实际复杂海洋环境中，水声量测信息呈现出未知或时变的统计特性。同时，由于受外部环境的干扰和多路径效应等因素的影响，基于宽带扩频的相干信号会发生干扰，估计的相关峰会产生错乱，导致水声定位系统测量信息出现没有规律性的野值。针对复杂水下环境中未知或时变的量测噪声特性，采用变分贝叶斯的方法对未知参数进行自适应估计。针对复杂水下环境中量测野值引起的量测噪声的厚尾特性，采用基于学生t分布的新型鲁棒处理的方法，下文将给出推导过程。

2.1 基于学生t分布的分层状态空间模型

对于一个厚尾量测噪声的线性状态空间模型，学生t后验概率密度函数(Probability Density Func-tion, PDF)可以视为无穷多个高斯PDF的混合，则似然PDF(|)可以表示为

(|)=St(;,,)

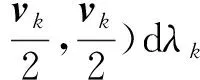
(42)

似然PDF(|)可以表示分层高斯的形式为

(43)

在贝叶斯推断中，尺度矩阵及其辅助的随机变量选择为共轭先验分布

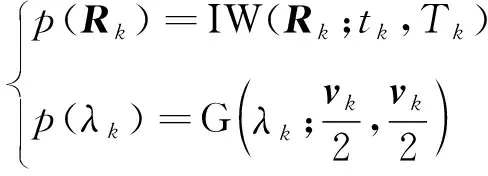
(44)

其中，为自由度参数，可以更新为伽马分布

()=G(;-1,-1)

(45)

(-1|1∶-1)更新为逆Wishart PDF，即

(46)

由于量测噪声的协方差特性是缓慢变化的，可通过来传递上一时刻的后验PDF，则先验参数和可分别表示为

(47)

(48)

2.2 基于学生t分布的新型鲁棒自适应滤波器

本节的目的是计算联合后验PDF(,,,|1∶)。然而，基于构建的分层高斯状态空间模型，无法获取后验PDF的一个封闭形式的解析解。因此，为了得到其近似解，本文利用变分贝叶斯(Variational Bayes，VB)方法来联合推断状态向量、尺度矩阵、辅助随机变量和自由度参数，即≜{,,,}。将(|1∶)表示为一个具有自由分解形式的近似后验PDF形式为

(|1∶)≈()()()()

(49)

其中，(·)表示近似的后验PDF。上述表达式的最优解可以通过最小化真实后验(,,|1∶)和近似后验()()()PDF的KL散度(Kullback-Leibler Divergence，KLD)来实现，则最优解满足以下的方程

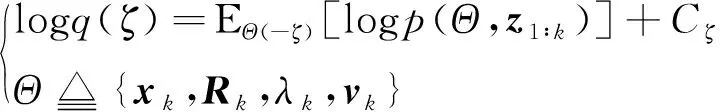
(50)

基于构建的分层高斯状态空间模型的条件独立性，状态向量、量测噪声的协方差阵、辅助随机变量和自由度参数分别更新为高斯分布、逆Wishart分布、伽马分布及其伽马分布，可以得到

G(;-1,-1)

(51)

根据方程(50)，log(,1∶)可以计算为

log(,1∶)=

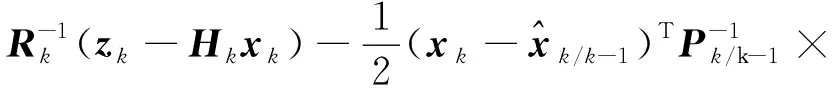
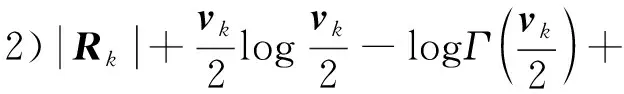
(52)

令分别等于、、、，将方程(50)代入方程(52)，其具体的推导过程类似于文献[12]和文献[13], 基于学生t分布的鲁棒自适应滤波算法，其执行的伪代码可以总结如表1所示。

表1 基于学生t分布的鲁棒自适应滤波算法

3 试验验证

为验证本文提出的基于SINS/USBL/DVL多源组合导航系统在实际水下环境中的导航性能，在广西省北海市周边的水域做了海试试验。试验开始前，将应答器预先布放在水底，其位置可由长基线的方法精确标定。试验系统设备的连接和原理图如图1所示。整个试验系统包含GPS、IMU、USBL、DVL这4个传感器及其他外围设备。其中，RTK-GPS和SINS组合的结果可作为位置信息的参考基准。

图1 试验系统设备的连接图Fig.1 Connection diagram of the test system equipments

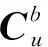
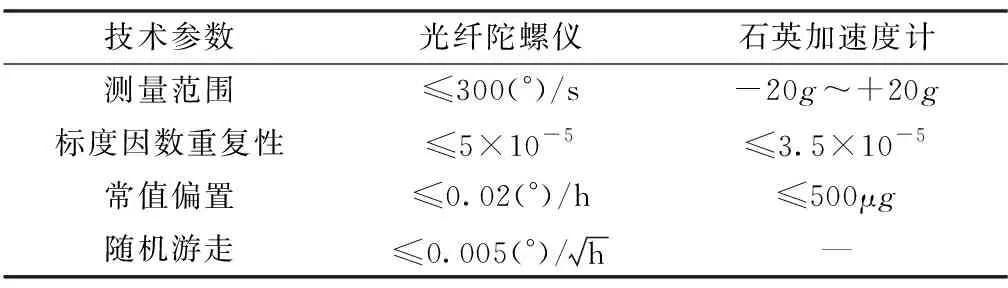
表2 IMU参数

表3 试验设备的主要参数表

在实际海试试验中，由于水下复杂环境的干扰和多路径效应等因素的影响，USBL和DVL实测的测量信息在很多时候都会有野值的干扰，有些是明显的野值，有些不明显。图2和图4所示为这次海试试验在一段时间内实测的水声数据。图3和图5所示为USBL和DVL有无野值时的概率密度对比图。

由图2和图4可以看出，USBL和DVL水声数据中有大量明显的野值存在，而且也有很多相对小的野值。一方面，假如通过简单识别并剔除的话会严重破坏数据的完整性，且为事后处理。USBL水声的数据更新频率本身就不是很高，大约2s才更新一个数据，简单剔除的话，量测更新的频率会更低；组合定位的曲线也比较曲折，不但会降低定位的精度，而且会导致对应GPS的时序也得做相应调整。另一方面，野值的存在会导致外部观测信息概率分布近似为厚尾分布而不服从高斯分布，如图3和图5所示。此时，传统的卡尔曼滤波已不是最优估计。

图2 USBL实测数据Fig.2 Data measured by USBL in real time

图3 概率密度对比Fig.3 Probability density comparison

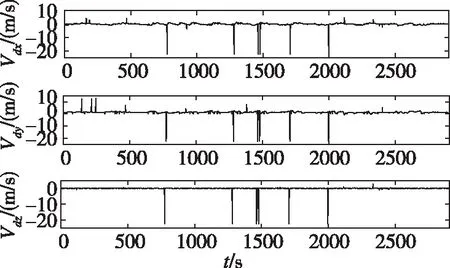
图4 DVL实测数据Fig.4 Data measured by DVL in real time

图5 概率密度对比Fig.5 Probability density comparison

因此，本文提出了基于学生t分布的SINS/USBL/DVL多源组合导航算法(Rst-SINS/USBL/DVL)，将其与基于学生t分布的SINS/USBL组合导航算法(Rst-SINS/USBL)、基于学生t分布的SINS/DVL组合导航算法(Rst-SINS/DVL)、SINS/USBL/DVL、SINS/USBL和SINS/DVL组合导航算法做比较，不同算法的定位误差曲线如图6和图7所示。表4给出了不同算法下定位误差统计的结果(RMSE)。

图6 东向定位误差Fig.6 East orientation errors

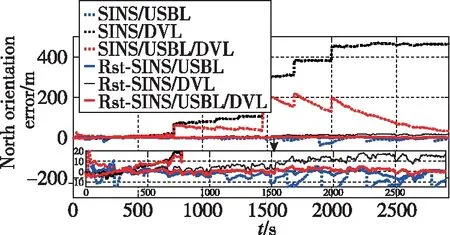
图7 北向定位误差Fig.7 North orientation error

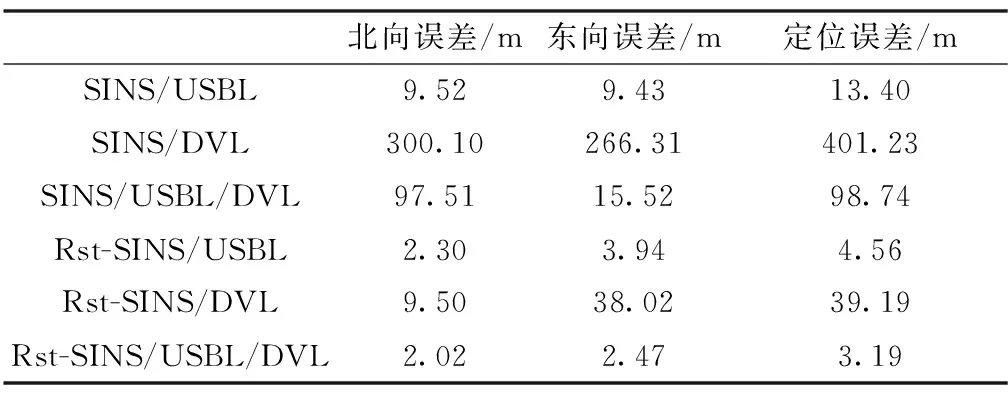
表4 定位统计的结果

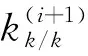
图8 滤波器参数分析Fig.8 Filter parameter analysis

结合图6、图7和表4统计结果，将提出的Rst-SINS/USBL/DVL与Rst-SINS/USBL、Rst-SINS/DVL做比较可以看出，Rst-SINS/USBL/DVL具有更好的定位精度。这是因为虽然USBL能够对SINS累积的位置误差起调制和校正作用，但是仍受限于USBL定位精度；同时，Rst-SINS/USBL组合的速度误差仍然很大，且Rst-SINS/USBL组合为区域内导航。因此，可以通过融合SINS/USBL/DVL的多源信息，利用DVL进一步抑制速度误差进而提高组合定位精度，实现长航时和广区域内导航。Rst-SINS/DVL组合导航虽然可以抑制速度误差，但是其位置误差随时间是发散的，且与初始的位置误差有关。因此，通过海试试验证明了本文提出的基于学生t分布的SINS/USBL/DVL多源组合导航算法的有效性和优越性，提高了组合定位的精度、鲁棒性和可靠性。

4 结论

针对复杂水下声场环境下水声量测信息的不确定性所引起的厚尾特性，本文推导了基于学生t分布的新型鲁棒自适应滤波器，通过提出的SINS/USBL/DVL多源信息融合的组合导航策略，提高了水下航行器导航与定位的精度和可靠性。

1)针对复杂水下环境下量测噪声未知和量测野值等不确定量测对定位精度的影响，将状态向量、量测噪声的协方差阵、辅助随机变量和自由度参数分别更新为高斯分布、逆Wishart分布、伽马分布及其伽马分布，基于学生t分布推导了新型的鲁棒自适应滤波算法，实现了对未知量测噪声方差的自适应估计和对量测野值的鲁棒处理。

2)推导了SINS/USBL/DVL多源信息融合的滤波模型，基于设计的集中卡尔曼滤波器，提高了组合定位的精度，能够满足水下航行器在复杂水下声场环境下高精度、长航时导航与定位的需求。