三重螺旋筋约束混凝土柱承载力影响参数分析

覃龙寿, 陈健伟, 莫琳琳,3, 周济, 陈宗平,4*

( 1.广西华蓝工程管理有限公司, 广西 南宁 530012;2.广西大学 土木建筑工程学院, 广西 南宁 530004;3.南宁学院 土木与建筑工程学院, 广西 南宁 530200;4.工程防灾与结构安全教育部重点实验室, 南宁 530004)

0 引言

螺旋箍筋约束混凝土柱因承载能力强、抗震性能好和便于施工安装等特点被广泛应用于工程实践中[1-4]。螺旋箍筋约束混凝土柱按截面形状不同可分为方柱和圆柱。由于螺旋箍筋无法有效约束混凝土方柱的4个角部[5],且拱效应使矩形箍筋对核心混凝土的约束作用分布不均匀,极易发生中部鼓曲,从而丧失对核心混凝土的约束作用,故螺旋箍筋约束混凝土圆柱的力学性能更为优越。然而,在柱截面尺寸的限制下,仅单层螺旋筋的约束能力难以满足设计规范对钢筋混凝土柱的延性要求[6]。

为此,有学者提出了多重螺旋箍筋约束钢筋混凝土的概念并开展了相关研究。宋力等[7]通过有限元分析研究了双层螺旋箍筋约束混凝土的横向约束力分布,结果表明,双层螺旋箍筋能有效约束混凝土的横向变形,对提高钢筋混凝土圆柱的极限承载力和延性有明显效果。Yang等[8]针对双层螺旋箍筋约束高强混凝土进行了试验研究,并提出了相应的高强约束混凝土应力-应变本构模型。Sun等[9]对比分析了混凝土强度等级、螺旋箍筋体积配箍率对双层螺旋箍筋约束混凝土圆柱受力性能的影响,试验结果表明,随着混凝土强度的提高,设置双层螺旋箍筋可以有效提高承载能力和延性。熊海明等[10]提出了一种三重螺旋箍筋复合约束混凝土圆柱,如图1所示,并对其进行了轴心受压试验,研究结果表明,三重螺旋箍筋约束混凝土圆柱的破坏过程及形态与双层螺旋箍筋约束混凝土圆柱相似,但具有更大的初始刚度、更好的变形能力和耗能能力。现有研究针对多重螺旋箍筋约束混凝土圆柱的研究中,涉及的变化参数较少,且主要集中在双层螺旋箍筋,尚未见有学者对三重螺旋箍筋约束混凝土圆柱开展系统性的参数分析。

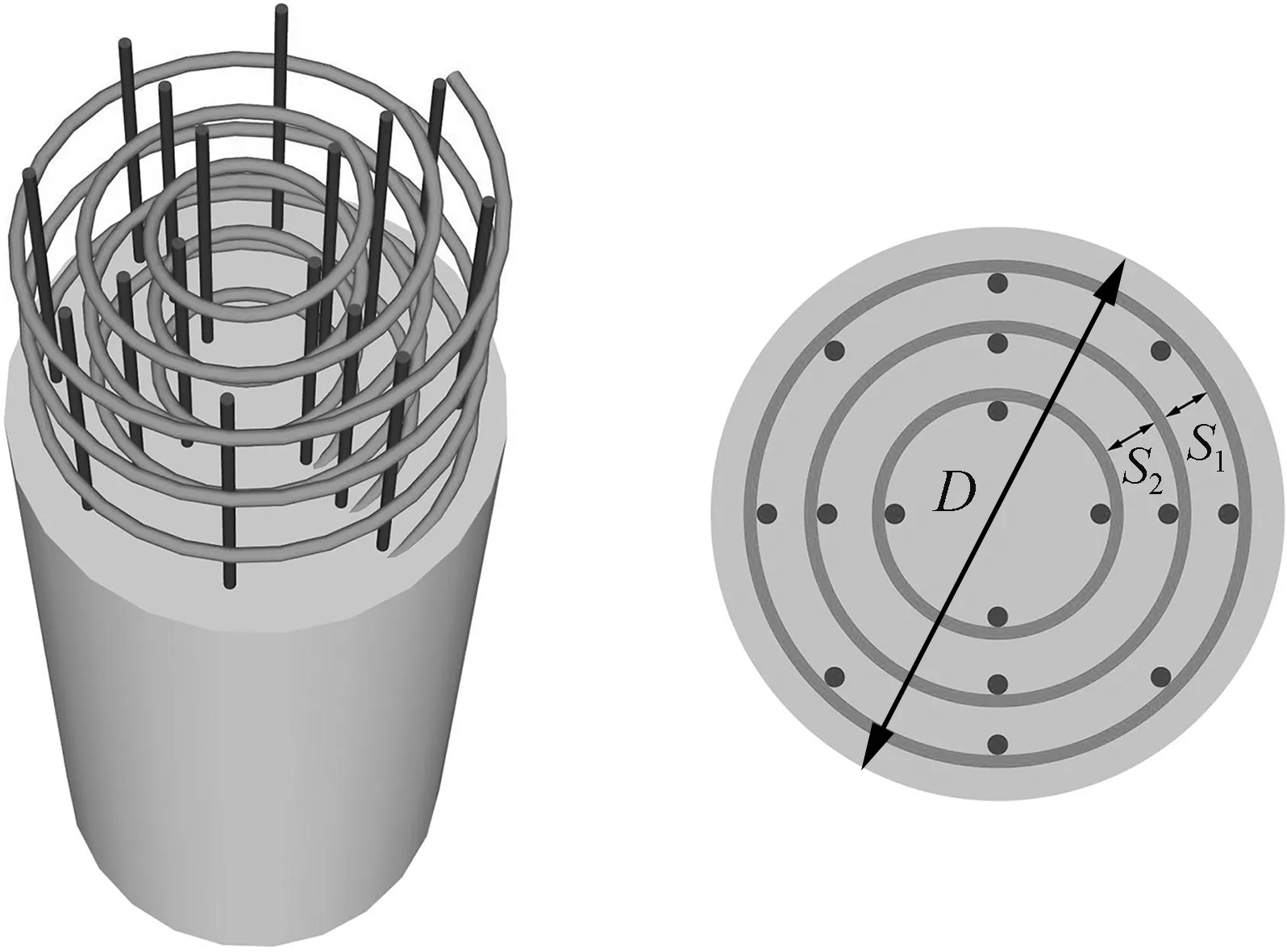
(a) 三维示意 (b) 二维示意

1 有限元模型

1.1 单元选取及网格划分

三重螺旋箍筋约束混凝土柱采用钢筋、混凝土分离式建模,如图2所示。保护层混凝土和核心区混凝土均采用C3D8R实体单元模拟,钢筋则全部采用T3D2桁架单元模拟。本文中忽略钢筋与混凝土间的粘结滑移,钢筋与混凝土单元通过Embedded Region的方式耦合。钢筋和混凝土的网格大小分别设置为20 mm和30 mm。

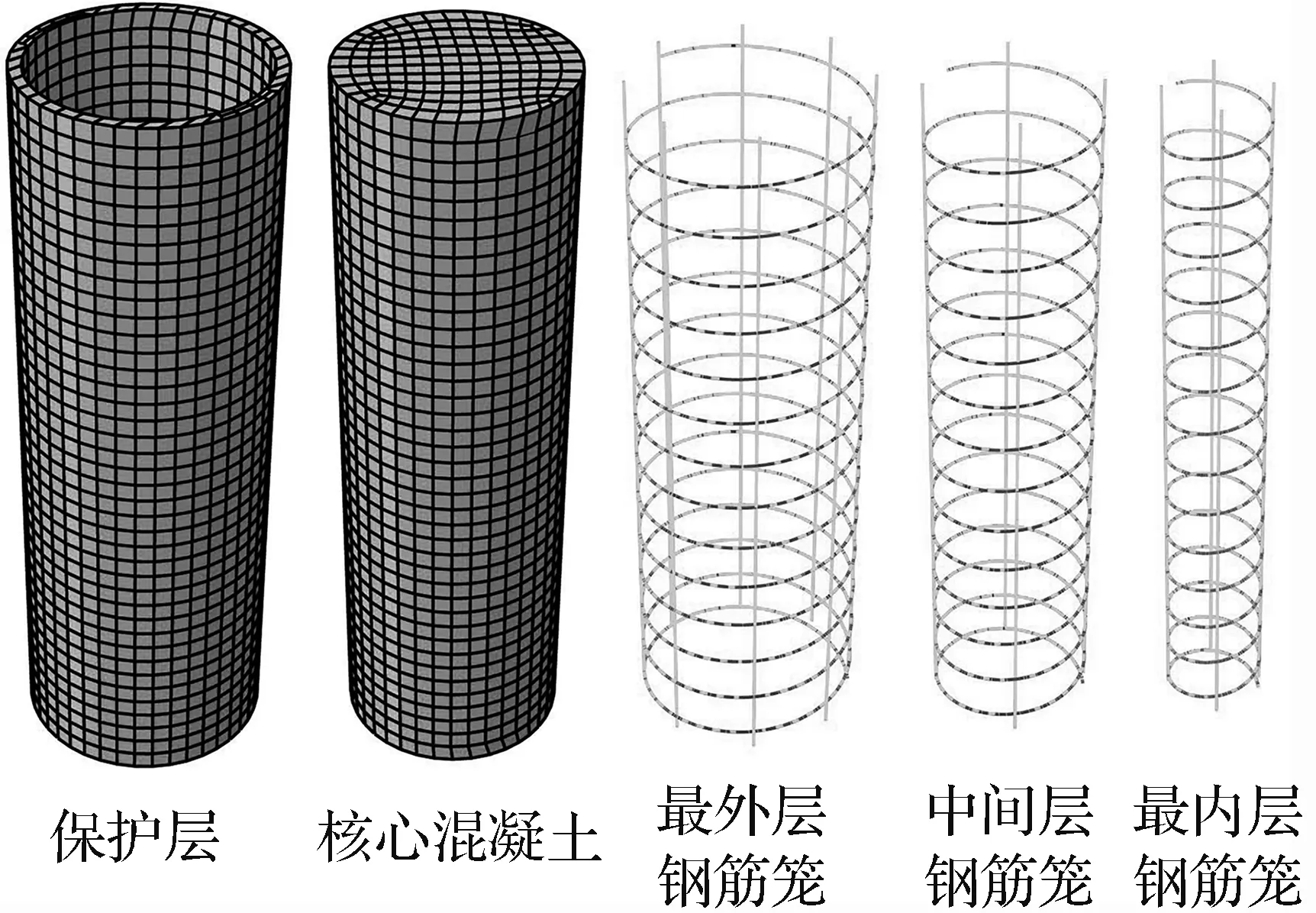
图2 有限元模型Fig.2 Finite element model

1.2 材料本构关系

混凝土材料模型选用塑性损伤模型,保护层混凝土的拉、压本构关系采用《混凝土结构设计规范》(GB 50010—2010)[11]中提出的混凝土单轴应力-应变关系,核心区混凝土本构关系采用Mander模型[12],为综合考虑各层螺旋箍筋约束作用对极限承载力的提高作用,参考文献[8],基于各层螺旋箍筋的约束区域面积对侧向约束应力进行加权处理,从而得到有效侧向应力fle,并代入Mander模型中进行计算,具体表达式为

(1)

式中：Ac为受约束区域总面积;A3、A2、A1分别为仅受最外层螺旋箍筋约束区域面积、同时受最外层及中间层螺旋箍筋约束面积和受三重螺旋箍筋约束区域面积;fl3、fl2、fl1分别为最外层螺旋箍筋提供的侧向应力、中间层螺旋箍筋提供的侧向应力、最内层螺旋箍筋提供的侧向应力。

钢筋均选用理想弹塑性模型,模型具体表达形式为

(2)

式中Es和Fy分别为钢筋弹性模量和屈服强度。

1.3 相互作用与边界条件

为了符合三重螺旋箍筋约束混凝土圆柱的实际受力情况,柱体的上下两端采用铰接方式连接,加载工况为柱顶位移加载。为了模拟混凝土保护层的开裂和剥落,当纵筋临近屈服时,采用生死单元的方法删除保护层混凝土单元以获得曲线下降段并加快计算速度[13]。

1.4 有限元模型验证

为验证本文中有限元模型的准确性,对文献[10]中的三重螺旋箍筋约束混凝土圆柱试件进行有限元分析,并与其试验结果进行对比。模型中,混凝土轴心抗压强度、钢筋屈服强度等参数均取试验实测值。有限元与试验结果对比见表1,可以看出有限元模拟得出的计算结果和试验值吻合良好,计算得出的三重螺旋箍筋约束混凝土圆柱极限承载力最小误差为2.30%,最大误差仅为6.79%,说明采用本文建立的有限元模型模拟三重螺旋箍筋约束混凝土圆柱的轴心受压力学行为具有可行性。

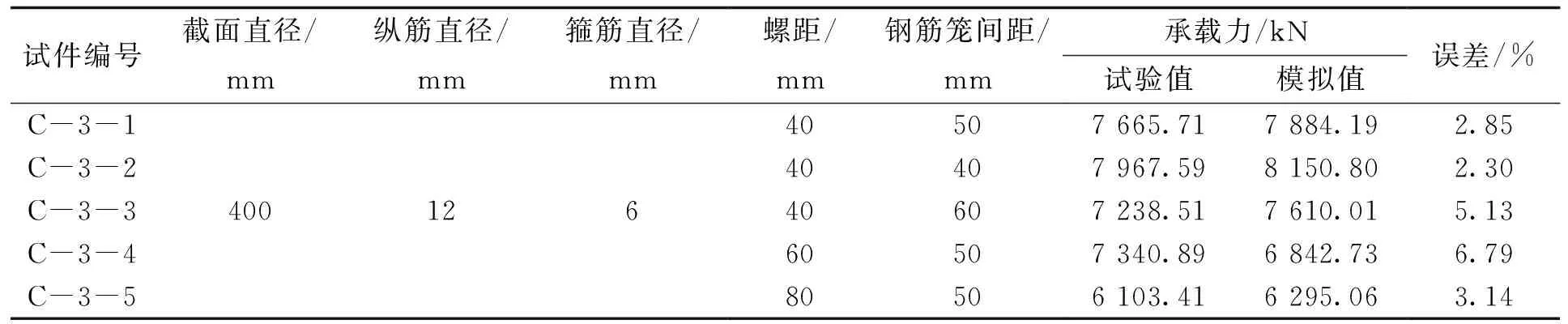
表1 试件极限承载力实测值与有限元结算结果对比Tab.1 Comparison of experiment and finite element calculation results

2 参数设置

本文中考虑的参数包括：①截面直径;②中间层钢筋笼至最外层钢筋笼间距;③最内层钢筋笼至中间层钢筋笼间距;④混凝土强度;⑤螺旋箍筋间距。将各因素间进行组合,得到1 024个试件的非线性有限元分析结果。表2总结了分析中所考虑的参数以及各参数对应的4个水平。模型中钢筋的弹性模量为2.07×105MPa,屈服强度为365 MPa,钢筋的泊松比取0.3。

表2 有限元分析主要设计参数Tab.2 Design parameters considered in the numerical study

3 有限元结果与分析

3.1 破坏模式

图3所示为模型在最终加载状态时的应力云图。从图中可以看出,三重螺旋箍筋约束混凝土圆柱中部发生横向膨胀变形,且钢筋均已屈服,材料性能得到充分发挥。在柱体截面中部,由于受到多层螺旋箍筋的复合约束,核心混凝土仍能保持较高的压应力。

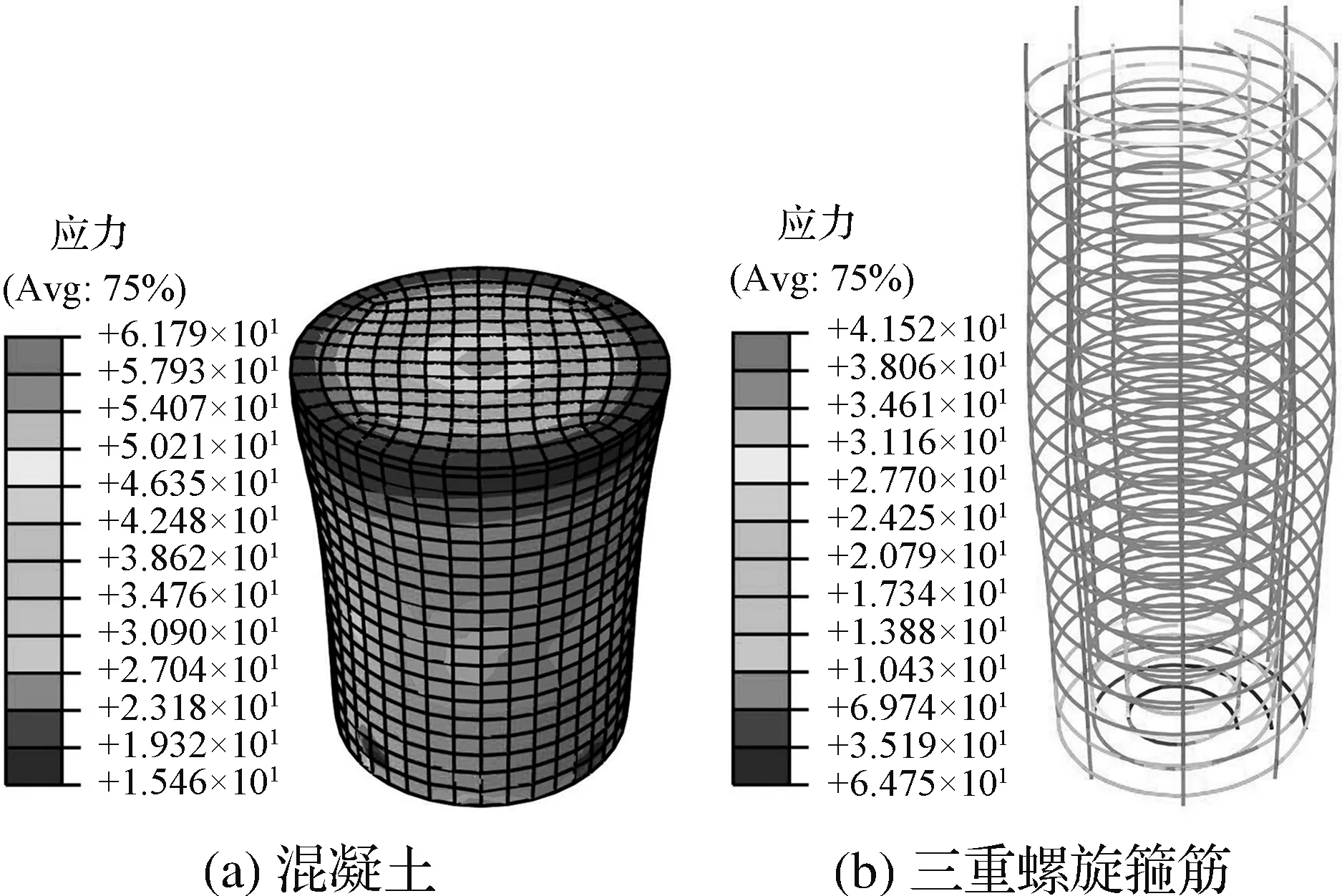
图3 试件破坏时应力云图Fig.3 Stress nephogram at failure

3.2 参数分析

为了直观反映各分析参数对试件极限承载力的影响,现定义归一化无量纲的极限承载力提高系数(Pmax-P0)/P0,其中,Pmax为三重螺旋箍筋约束混凝土圆柱在各因素协同作用下的极限承载力,P0为相同试件仅配置最外层螺旋箍筋的极限承载力(即中间层和最内层的螺旋箍筋体积配箍率ρst1、ρst2均为0)。各因素影响下的(Pmax-P0)/P0箱线图如图4所示，图中总结了截面直径、混凝土强度、各层箍筋间距离以及螺旋箍筋间距在内部两层螺旋箍筋复合约束作用下对三重螺旋箍筋约束混凝土圆柱极限承载力的影响。计算结果以箱线图(box-and-whisker plots)的形式进行展现,它主要用于反映原始数据分布的特征[14],还可以进行多组数据分布特征的比较,其中,箱子的中线代表中位数,箱子的下界线及上界线分别代表数据的下四分位数和上四分位数,

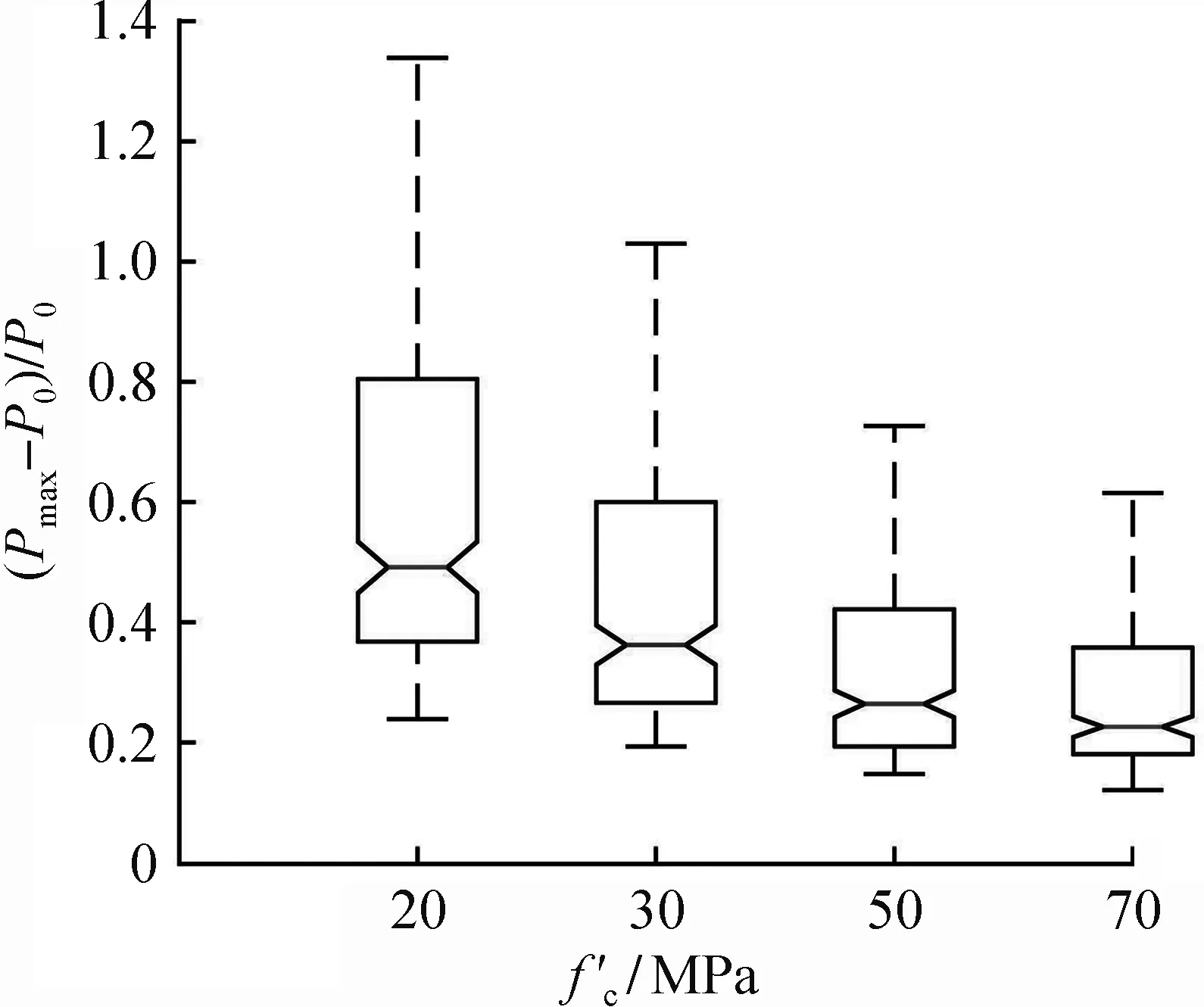
(a) 混凝土强度

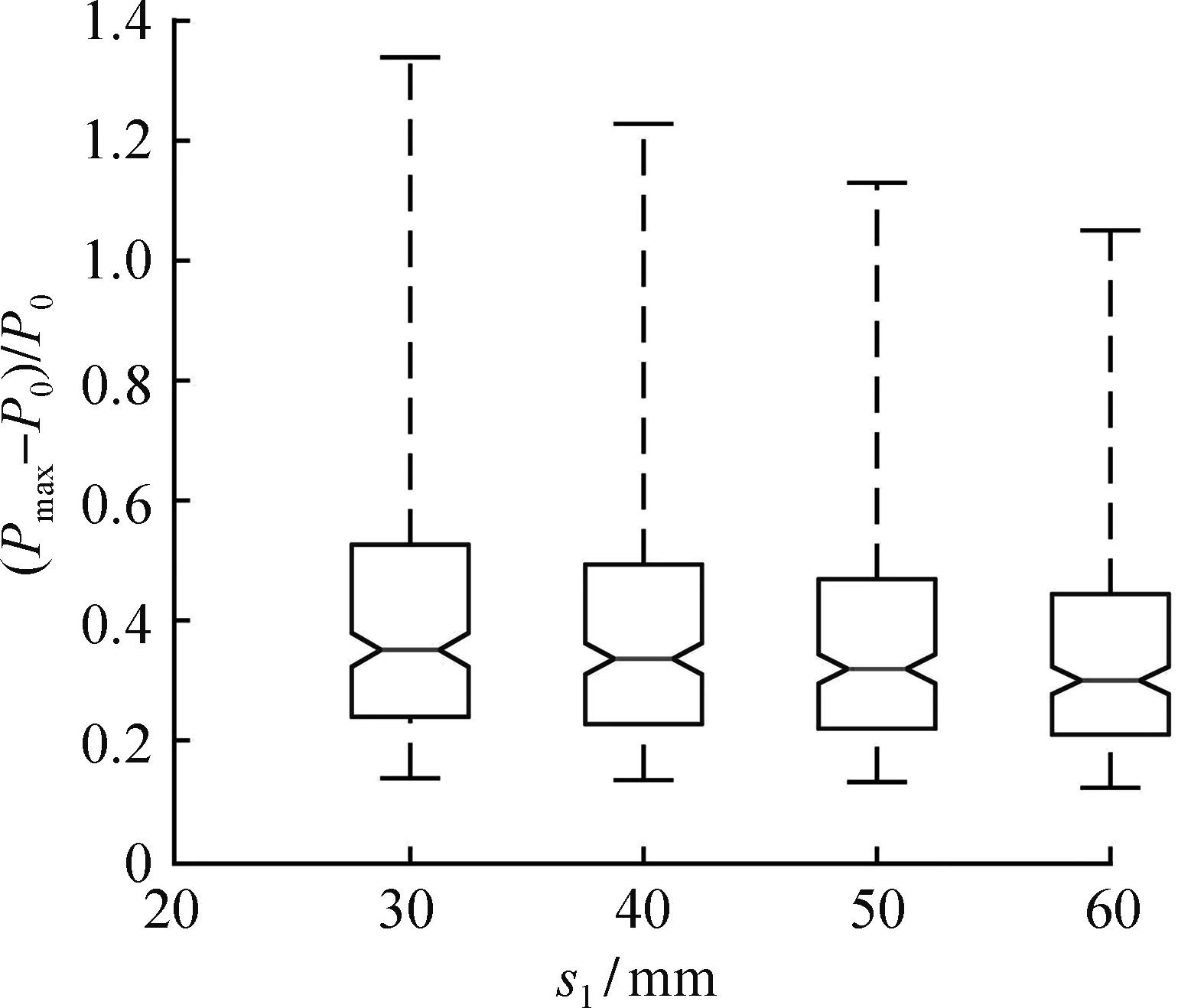
(b) 中间层钢筋笼与最外层钢筋笼间距

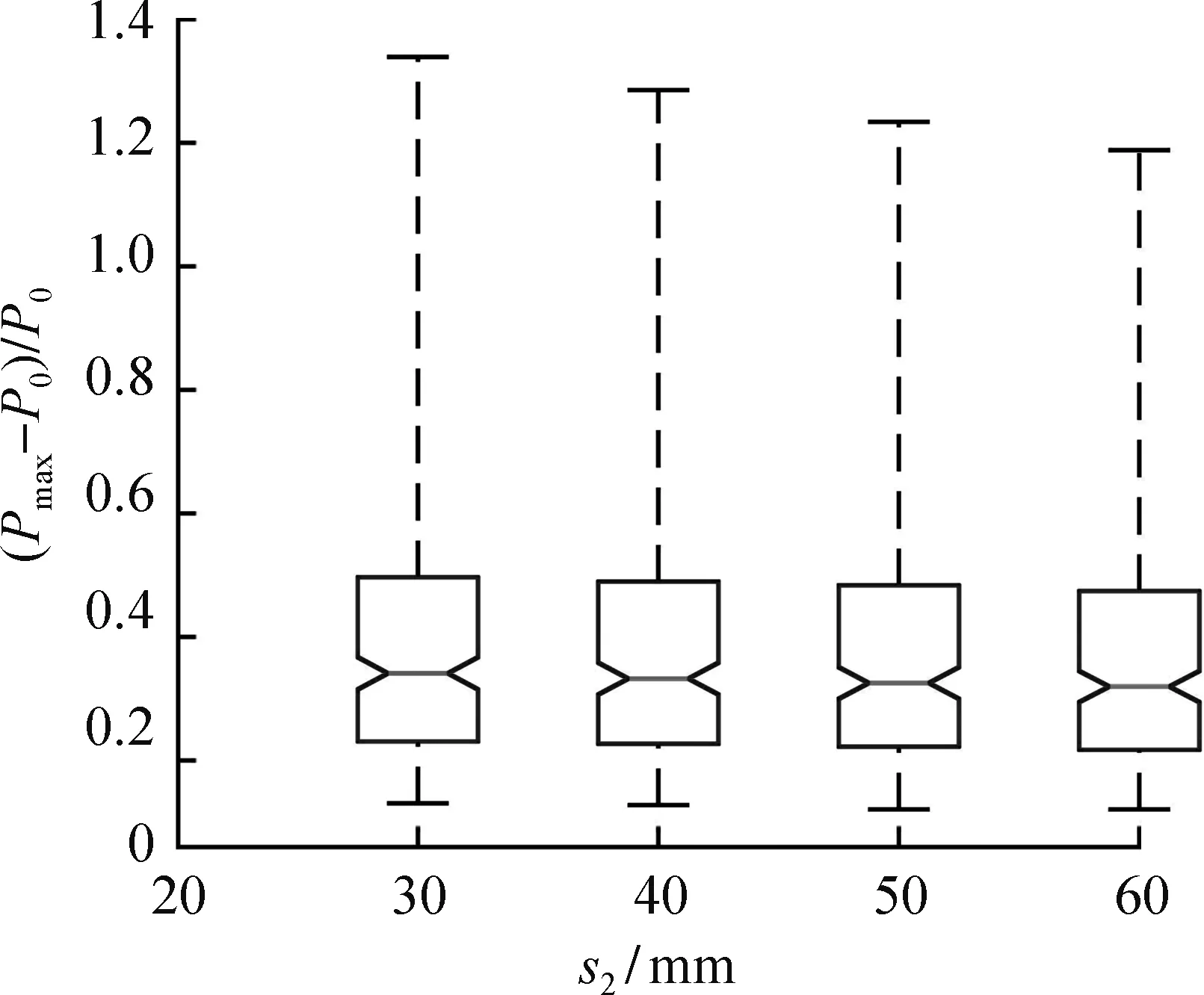
(c) 最内层钢筋笼与中间层钢筋笼间距

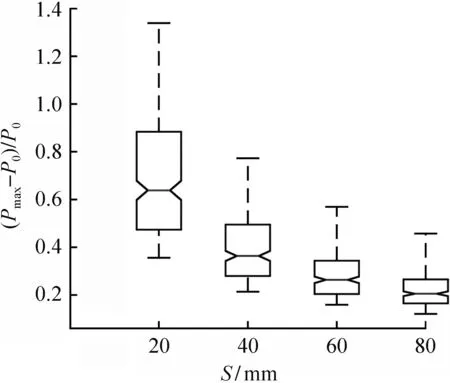
(d) 螺旋箍筋间距

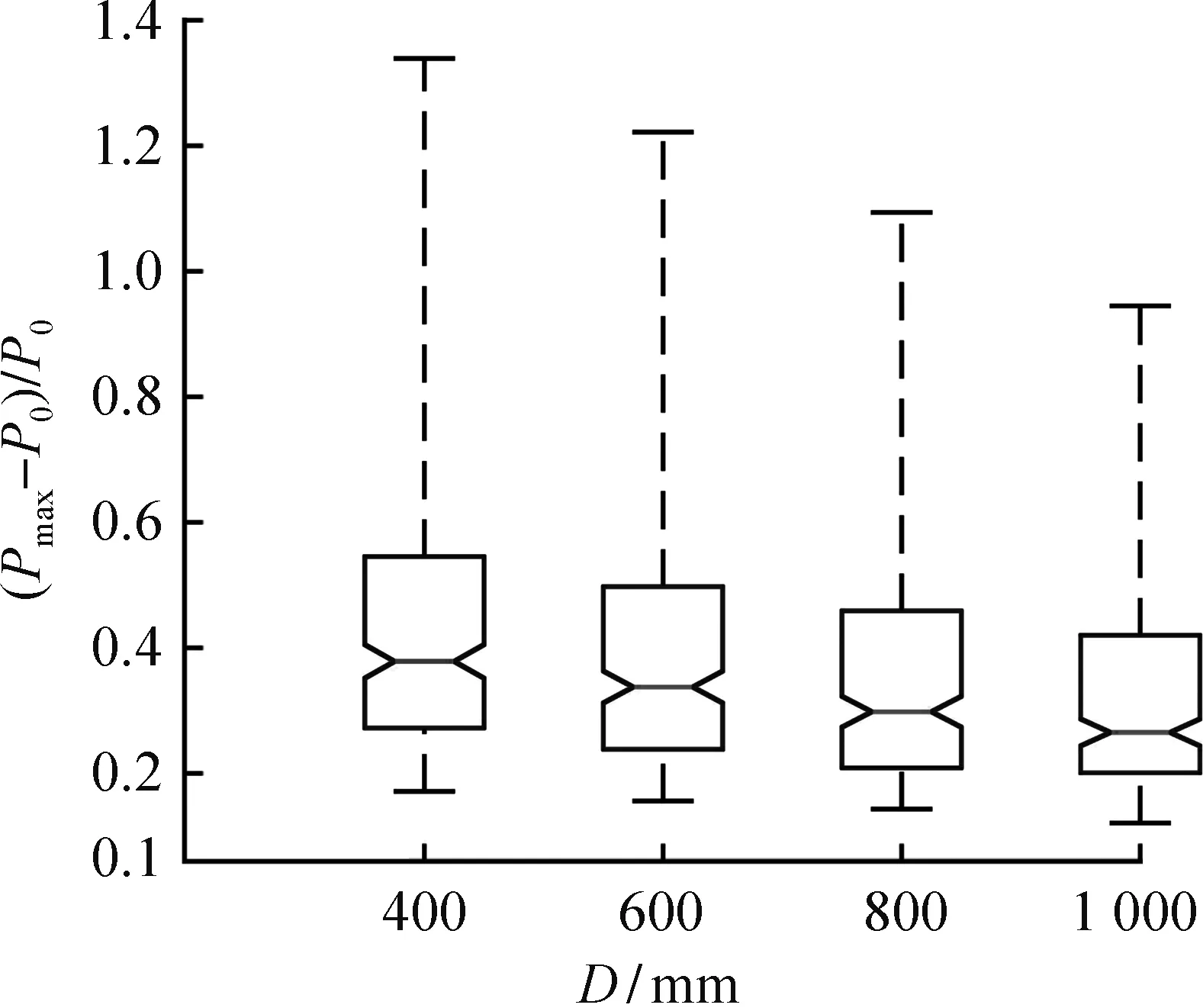
(e) 截面直径

上下界线之间的距离表示四分位差,箱子中部的缺口代表中位数的置信区间,箱子两端各向外延伸出一条线段,表示数据完整的分布区间。

3.2.1 混凝土强度

图4(a)为混凝土强度fc′对三重螺旋箍筋约束混凝土圆柱极限承载力提高系数的影响。从图中可以看出,(Pmax-P0)/P0随着混凝土强度的提高而减小,当混凝土强度从20 MPa增加到70 MPa时,其箱线图的中位数由0.49下降到0.22,极限承载力提高系数降低了55.1%,说明高强混凝土脆性的加强会减小侧向膨胀,从而极大地削弱横向钢筋对核心混凝土的被动约束作用,该现象与文献[15]提出的约束混凝土本构模型一致。从图中也可以看出,在本文所研究的参数范围内,混凝土强度影响下的极限承载力提高系数箱线图存在一定的偏度,表现为数据分布整体偏向中位数下方。另外,对比各混凝土强度对应箱子的四分位差可知,当混凝土强度较低时,极限承载力提高系数的离散性较大,分布区间为0.25～1.36,随着混凝土强度的提高,离散性逐渐减小,(Pmax-P0)/P0的分布区间变为0.15～0.62,说明在本文所考虑参数范围内,混凝土强度对于试件承载力的提升逐渐起主导作用。

3.2.2 钢筋笼间距

图4(b)为中间层钢筋笼与最外层钢筋笼间距s1对三重螺旋箍筋约束混凝土圆柱极限承载力提高系数的影响。由图可知,随着s1的增加,极限承载力提高系数呈线性降低,但影响并不显著,s1由30 mm增加到60 mm时,其箱线图的中位数由0.35下降到0.29,极限承载力提高系数降低了15.3%。当s1大于30 mm时,各箱子的四分位差几乎保持不变,说明s1的变化对三重螺旋箍筋约束混凝土圆柱极限承载力提高系数的影响较小,但极限承载力提高系数的最大值下降相对明显,由1.34下降至1.05,降幅为21.6%。

图4(c)为最内层钢筋笼与中间层钢筋笼间距s2对三重螺旋箍筋约束混凝土圆柱极限承载力提高系数的影响。由图可知,随着s2的增加,各箱子的四分位差始终保持不变,且其中位数维持在0.32左右。说明在本文所考虑的参数范围内,s2对试件极限承载力提高系数的影响较为稳定。与s1相比,s2影响下的极限承载力提高系数最大值降幅进一步减小,仅为10.5%。造成上述现象的原因是中间层螺旋箍筋与最内层螺旋箍筋相比,对核心混凝土形成的有效约束面积更大,故s1的减小对试件承载力的提升效果更为明显。

3.2.3 螺旋箍筋间距

图4(d)为螺旋箍筋间距对三重螺旋箍筋约束混凝土圆柱极限承载力提高系数的影响。由图可知,在螺旋箍筋间距较小时,箱子的四分位差较大,横向箍筋对试件承载能力的提升效果(Pmax-P0)/P0最大可达1.36,这是由于螺旋箍筋间距的减小会减小竖直方向上的拱效应,使侧向约束力分布更为均匀,从而增强核心混凝土的竖向承载性能。当螺旋箍筋间距S从20 mm增加至80 mm,(Pmax-P0)/P0中位数下降了62.1%。而随着螺旋箍筋间距的增加,极限承载力提高系数的变动范围逐渐缩小,当螺旋箍筋间距S从20 mm增加至80 mm,四分位差由0.52降至0.15,说明此时(Pmax-P0)/P0主要受螺旋箍筋间距控制,且在这一过程中,箱子的中位数不断减小,但下降幅度逐渐减缓,这主要是由螺旋箍筋间距的增加使得三重螺旋箍筋约束混凝土圆柱的体积配箍率减小所导致的。

3.2.4 截面直径

图4(e)为三重螺旋箍筋约束混凝土圆柱的截面尺寸对极限承载力提高系数的影响。从图中可以看出,随着柱体截面直径的增大,螺旋箍筋对试件极限承载力的提高作用逐渐降低,当截面直径从400 mm增加至1 000 mm时,(Pmax-P0)/P0的中位数降低了21.1%,而且柱体截面尺寸影响下的极限承载力提高系数箱线图的四分位差基本保持不变。柱体截面尺寸对极限承载力提高系数产生上述影响的原因,主要是由于本文参数研究中,各钢筋笼间距固定为4个水平,随着柱体截面尺寸的变化,各层螺旋箍筋的约束半径也随之增大,从而导致三重螺旋箍筋约束混凝土圆柱的体积配箍率减小,使得横向钢筋对核心混凝土的侧向约束作用降低。

3.2.5 不同参数间相互作用

为进一步分析螺旋箍筋体积配箍率及其与其他因素共同作用下三重螺旋箍筋约束混凝土圆柱的极限承载力变化规律,额外添加中间层螺旋箍筋体积配箍率ρst1和最内层螺旋箍筋体积配箍率ρst22组研究参数,各包含6个水平:0.25%、0.50%、1.00%、1.50%、2.00%、2.50%,研究其与试件截面D和混凝土强度的协同作用对三重螺旋箍筋约束混凝土圆柱的极限承载力。

图5展示了混凝土强度为20 MPa时,试件极限承载力提高系数(Pmax-P0)/P0随截面尺寸和螺旋箍筋体积配箍率的变化规律。从图中可以看出,(Pmax-P0)/P0随中间层螺旋箍筋的体积配箍率增加而增大,且由于核心区约束作用的增强,最内层螺旋箍筋体积配箍率的增加亦会使(Pmax-P0)/P0进一步线性增大,但当试件截面尺寸D增至1 000 mm且中间层螺旋箍筋体积配箍率处于1.0%～2.5%时,最内层螺旋箍筋体积配箍率对(Pmax-P0)/P0的增幅逐渐减小,表现出非线性。

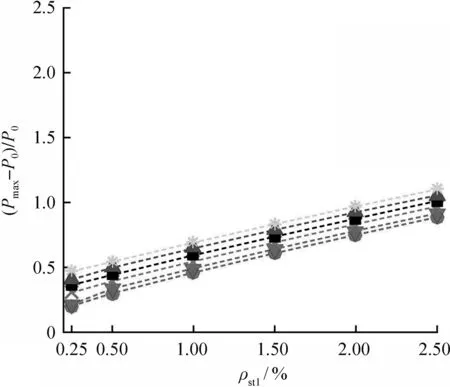
(a) D=400 mm时ρst1和ρst2的影响

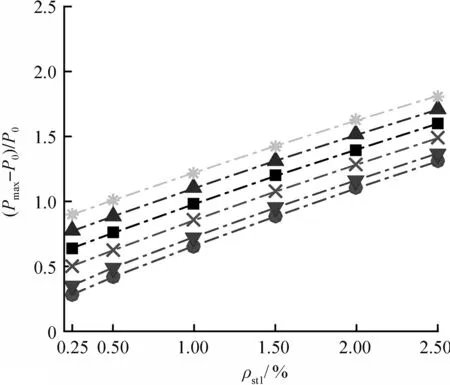
(b) D=600 mm时ρst1和ρst2的影响

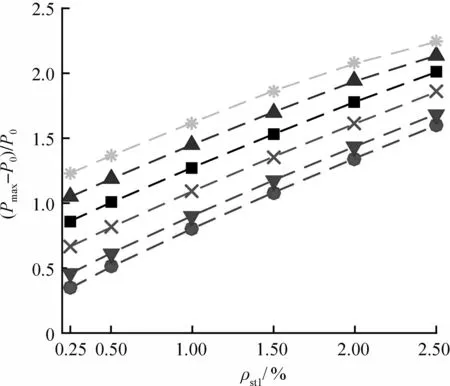
(c) D=800 mm时ρst1和ρst2的影响

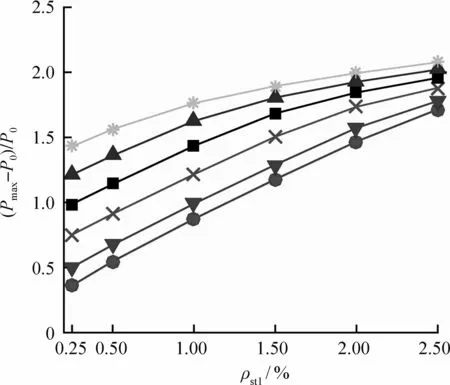
(d) D=1 000 mm时ρst1和ρst2的影响

图5 螺旋箍筋体积配箍率对(Pmax-P0)/P0的影响Fig.5 Effect of volumetric ratio of transverse steel on(Pmax-P0)/P0

图6所示为不同最内层螺旋箍筋体积配箍率ρst2作用下,试件截面尺寸D和中间层螺旋箍筋体积配箍率ρst1对(Pmax-P0)/P0的影响。从图中可以看出,当最内层螺旋箍筋体积配箍率处于0.25%～1.00%范围时,(Pmax-P0)/P0随着试件截面尺寸的增大而增大,但增大的趋势逐渐减缓,另外,当中间层螺旋箍筋体积配箍率较小时,(Pmax-P0)/P0受试件截面尺寸D影响的程度较小。当最内层螺旋箍筋体积配箍率ρst2处于1.00%～2.5%范围内且中间层螺旋箍筋体积配箍率处于1.5%～2.5%时,试件截面直径从400 mm增至600 mm,(Pmax-P0)/P0最多可从1.1增至1.8,然而截面直径继续从800 mm增加至1 000 mm时,(Pmax-P0)/P0却从2.3降至2.0。在本文所考虑的参数范围内,当混凝土强度提高时,同样能得到与前述相似的情况。上述结果说明,各层螺旋箍筋的约束效应对三重螺旋箍筋约束混凝土圆柱极限承载力的影响显著,表现出较强的非线性,且很大程度上依赖于柱体直径和钢筋体积配筋率。造成图5及图6所描述的现象,主要是由于随着试件截面的增大,由于外部箍筋的有效约束面积更大,其所提供的被动约束在核心混凝土侧向膨胀作用下更易发挥,而由于更靠近截面中心,所受混凝土侧向膨胀作用较少,故此时最内层螺旋箍筋对试件承载力的影响逐渐减小。

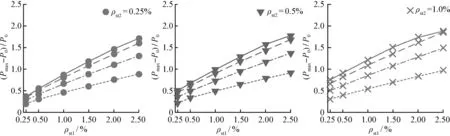
(a) ρst2=0.25%时ρst1与截面直径的影响 (b) ρst2=0.5%时ρst1与截面直径的影响 (c) ρst2=1%时ρst1与截面直径的影响

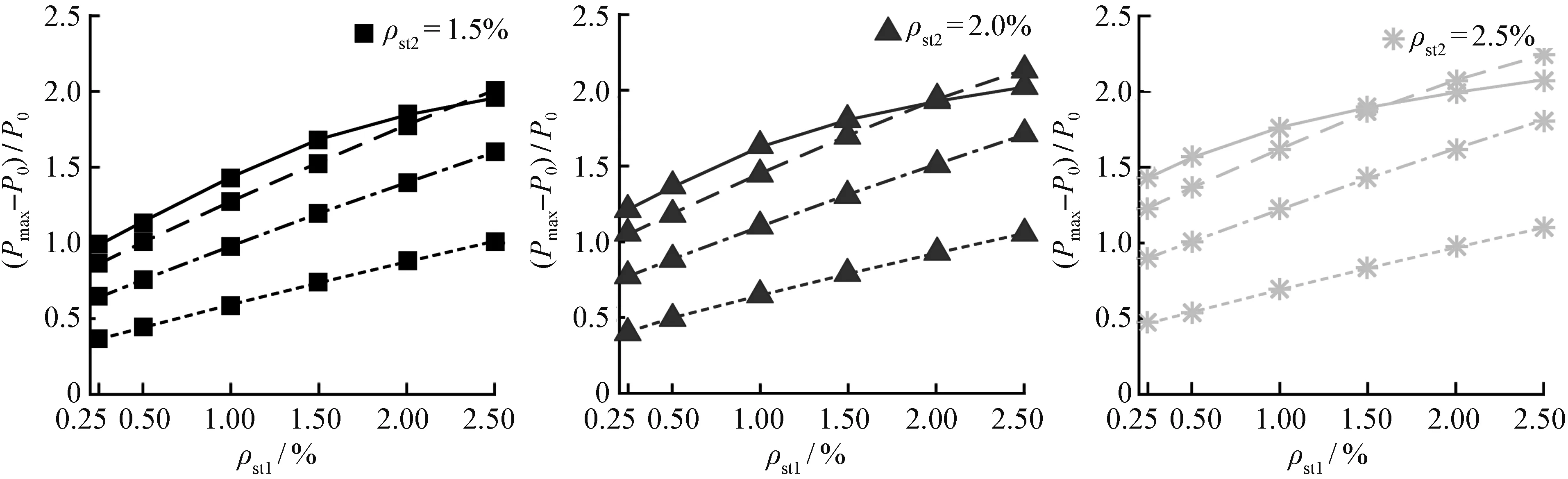
(d) ρst2=1.5%时ρst1与截面直径的影响 (e) ρst2=2%时ρst1与截面直径的影响 (f) ρst2=2.5%时ρst1与截面直径的影响

图6 截面直径对(Pmax-P0)/P0的影响Fig.6 Effect of section diameter on(Pmax-P0)/P0

图7为在不同混凝土强度条件下,(Pmax-P0)/P0随中间层及最内层螺旋箍筋体积配箍率的变化情况。由图可见,(Pmax-P0)/P0始终随着螺旋箍筋体积配箍率的增大而增大,且在混凝土强度较低时,螺旋箍筋体积配箍率对(Pmax-P0)/P0的提升更为明显。当固定中间层螺旋箍筋体积配箍率或最内层螺旋筋体积配箍率为一定值1.5%时,(Pmax-P0)/P0随最内层螺旋筋体积配箍率的变化情况与随最内层螺旋筋体积配箍率的变化情况有所不同,但两者的差别随着混凝土强度的增加而逐渐减小,说明此时混凝土强度对试件承载力的提升起主导作用,与前文所得出的结论一致。从图中还可以发现,在试件截面尺寸不变的情况下,当中间层螺旋箍筋体积配箍率大于最内层螺旋箍筋体积配箍率时,试件的极限承载力提高系数(Pmax-P0)/P0较大,即此时的用钢量分配对三重螺旋箍筋约束混凝土圆柱极限承载力的提升效果更为明显,横向钢筋的约束效率更高。

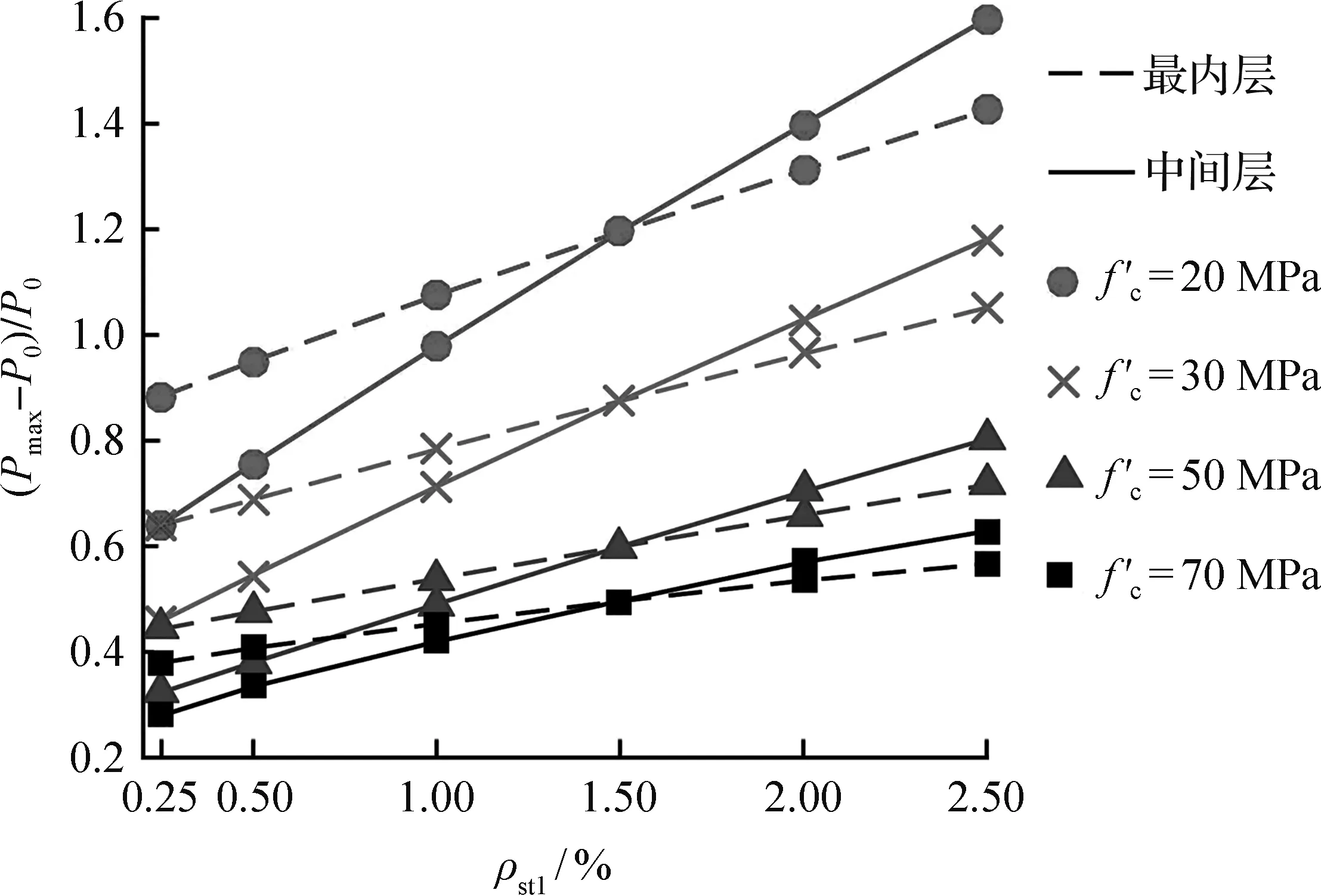
图7 混凝土强度对(Pmax-P0)/P0的影响Fig.7 Effect of concrete strength on (Pmax-P0)/P0

3.2.6 相对侧向应力

图8所示为有限元分析结果中,各试件的中间层螺旋箍筋相对侧向应力fl1/fc′和最内层螺旋箍筋相对侧向应力fl2/fc′与其相对应(Pmax-P0)/P0,图中实线为拟合得出的相对侧向应力与极限承载力提高系数之间的趋势线,拟合函数形式为分子和分母分别为二阶和一阶多项式的有理函数[16]。从图中可以看出,当相对侧向应力较低,即fl1/fc′、fl2/fc′<0.05时,(Pmax-P0)/P0基本上随着相对侧向应力的增加线性增长,说明对于螺旋箍筋体积配箍率较小的试件,(Pmax-P0)/P0主要受相对侧向应力控制。随着相对侧向应力的增加,(Pmax-P0)/P0增长的趋势逐渐减弱,且由于对核心混凝土的有效约束面积较小,所受核心混凝土侧向膨胀作用较弱,最内层螺旋箍筋相较于中间层螺旋箍筋的增长削弱趋势更为明显。当fl2/fc′>0.1时,随着最内层螺旋箍筋相对侧向应力的增加,(Pmax-P0)/P0的增长幅度放缓。另外,图中还给出了拟合趋势线的决定系数R2,对比中间层与最内层螺旋箍筋的决定系数R2可发现,中间层螺旋箍筋的决定系数(R2=0.728)大于最内层螺旋箍筋的R2=0.489),说明最内层螺旋箍筋相对侧向应力fl2/fc′与(Pmax-P0)/P0间的关系较为离散,而中间层螺旋箍筋的相对侧向应力fl1/fc′与(Pmax-P0)/P0的相关性更强,即fl1/fc′能更好地描述多重螺旋箍筋约束效应对试件极限承载力的提高作用。

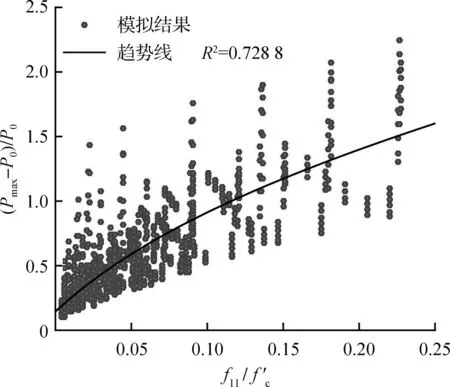
(a) 中间层螺旋箍筋

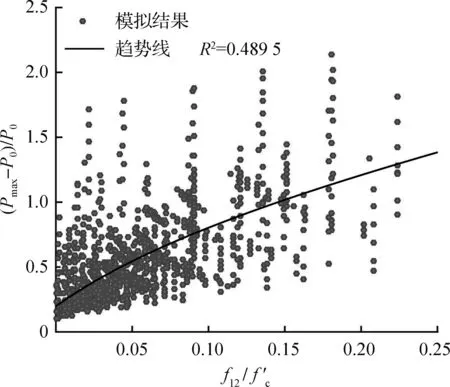
(b) 最内层螺旋箍筋

4 结论

本文基于1 024个三重螺旋箍筋约束混凝土圆柱的精细化弹塑性有限元模拟结果,研究了内部多重横向钢筋约束对三重螺旋箍筋约束混凝土圆柱轴向极限承载力的影响。为直观反映出各因素对三重螺旋箍筋约束混凝土圆柱极限承载力的影响,定义了极限承载力提高系数(Pmax-P0)/P0。分析考虑的关键设计参数包括试件截面直径、混凝土强度、中间层和最内层螺旋箍筋间距及其体积配箍率、各层钢筋笼间距,得到如下主要结论:

① 降低混凝土强度和螺旋箍筋间距均能使重螺旋箍筋约束混凝土圆柱的极限承载力提高系数(Pmax-P0)/P0明显增大,而截面直径D、中间层螺旋箍筋到最外层螺旋箍筋间距s1和最内层螺旋箍筋到中间层螺旋箍筋间距s2对(Pmax-P0)/P0的影响较小,其中,与s2相比,s1对(Pmax-P0)/P0的影响更为明显。

② 中间层螺旋箍筋体积配箍率ρst1、最内层螺旋箍筋体积配箍率ρst2和截面直径D之间的相互作用对(Pmax-P0)/P0的影响存在较强非线性。当最内层螺旋箍筋体积配箍率ρst2∈[1.0%, 2.5%]、中间层螺旋箍筋体积配箍率ρst1∈[1.5%, 2.5%]且试件截面直径D∈[400, 800]时,(Pmax-P0)/P0随截面直径的增大而增大；然而由于最内层螺旋箍筋受到的核心混凝土侧向膨胀相对外部箍筋进一步减小,其提供的被动约束力下降,故截面直径继续从800 mm增加至1 000 mm时,(Pmax-P0)/P0却随之降低了13%。

③ 中间层螺旋箍筋体积配箍率ρst1大于最内层螺旋箍筋体积配箍率ρst2时,内部横向钢筋对三重螺旋箍筋约束混凝土圆柱极限承载力的提高效果更为显著。

④ 当相对侧向应力小于0.05时,相比于最内层螺旋箍筋相对侧向应力fl2/fc′,中间层螺旋箍筋相对侧向应力fl1/fc′对(Pmax-P0)/P0的提高更为显著,且该参数与(Pmax-P0)/P0的相关性更强,能更好地描述内部横向钢筋对三重螺旋箍筋约束混凝土圆柱极限承载力的影响。