基于块坐标下降算法的优化哈希数据流频率估计

钟章生, 袁智勇

(南昌理工学院 计算机信息工程学院, 江西 南昌 330013)

0 引言

流媒体模型在搜索查询监控、网络流量监控等应用中发挥了极其重要的作用,在这些应用中最基本的问题之一是频率估计,即在输入流中,估计每个元素的发生次数[1-2]。数据流通常具有大容量的特征,因此,如何实现大型流媒体数据的频率估计成为了研究的热点问题。

Sketches是处理流媒体数据的最强大工具之一,它是一种数据结构,可以表示为输入的线性变换。Lu等[3]提出一种基于Rhombus Sketch的可动态调整的Sketch算法:DARS Sketch。该算法根据对流数据规模的估计,调整多层Sketch层级结构的内存分配,保证数据的存储位置在内存调整前后是一致的。Guo等[4]基于二项式分布和中心极限定理,结合Count-min Sketch处理大数据流的事件频率表。Yang等[5]提出了一种基于桶sketch的用于覆盖聚类和多样性最大化问题的空间高效滑动窗口算法,有效实现了流计算中的频率估计。虽然上述方法取得了一定效果,但是上述频率估计任务的估计精度极大地依赖于随机哈希,导致估计精度稳定性较低,可行性较差。

为了进一步提升估计精度,有大量文献将深度学习算法引入到流媒体数据频率估计中。Pinckaers等[6]提出了一种基于深度卷积神经网络的流媒体频率估计算法,通过卷积神经网络(convolutional neural networks, CNN)处理元素的列集,从而提升算法的适用性。甘元艺[7]提出了一个面向流的大数据应用的延迟和资源感知调度框架(Lr-Stream),旨在优化延迟和吞吐量,并且利用深度Q网络对系统指标进行了全面评估。Zhang等[8]提出了一种基于强化学习和神经网络学习的调度算法流式数据排序,用于在单处理器上处理受有限存储大小和排序顺序正确性约束的流式数据。赵鹏等[9]使用可解释的机器学习方法学习连续和混合整数凸优化问题最优解背后的策略,作为其关键参数的函数,对大型视频流数据实现频率估计。虽然上述方法利用深度学习的强非线性映射能力极大地提升了频率估计的准确性;但是由于流媒体数据规模较大,加上深度学习的训练要求较高,因此导致计算成本较高,很难实现实时估计功能。

为了解决上述2个问题,本文提出了一种基于块坐标下降算法的优化哈希数据流频率估计，并且通过实验结果证明了所提出方法的有效性。

1 相关理论

1.1 随机Sketches方法

用索引u表示变量,索引i和k表示变量标号,索引j表示存储桶。为便于标记,根据上下文使用符号u或i表示元素;以此类推,使用这2种方法中的任何一种对频率进行索引。

，

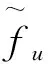
(1)

即该元素在S中出现的次数;本文中,1A表示事件A的指示函数。假设S和U都是较大的,因此希望在比min{|S|,|U|}小得多的空间中实现准确估计。在额外的假设下,即已经观察到的输入流的前缀S0=(u1,u2,…,u|S0|),其中|S0|≪|S|。

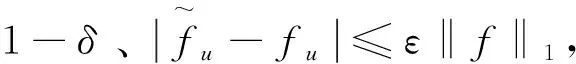
1.2 基于学习的方法

另外,分配给Heavy-hitter的每一个bheavy唯一桶都应保持相关元素的频率和元素名称ID。如上文所述,这可以通过使用具有开放寻址的哈希来实现,由此它足以将哈希的ID存储为logbheavy+t位,以确保不会与概率1-2-t发生冲突。logbheavy+t与每个计数器的位数相当,唯一存储桶的空间是普通存储桶的2倍。从理论和经验上看,学习增强算法都优于传统的完全随机算法，然而,该方法仍然是启发式的,不能保证获得最佳性能。

2 基于块坐标下降算法的优化哈希数据流频率估计

本文两阶段方法的工作原理如下。在第一阶段,流前缀中出现的元素根据其观察到的频率以最佳方式分配给桶,从而使频率估计误差最小化,同时,将相似的元素映射到相同的桶。与基于CMS的方法相反,在所提出的方法中,元素频率的估计是映射到同一桶的所有元素的频率的平均值,因此,本文目标是将“相似”元素分配给同一个桶。在第二阶段,一旦对前缀中出现的元素进行了优化分配,将根据元素的特征训练一个分类器,将元素映射到桶。通过这种方法,能够提供前缀中未出现的不可见元素的估计值,因此不会记录它们的频率。

提出的哈希方案包括一个哈希表,将前缀中出现的元素ID映射到桶和学习的分类器。此外,对于每个桶,需要保持其中映射的所有元素的频率之和。在流处理期间,一旦估计器准备就绪,每当前缀中出现的元素重新出现时,增加元素映射到的桶的计数器,即聚合频率。最后,为了实现任何给定元素的计数查询,只需通过哈希表或分类器输出映射元素的桶的当前平均频率。

2.1 学习最佳哈希方案

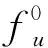
(2)

参数λ∈[0,1]控制哈希方案之间的权衡,这些哈希方案映射到相同的桶元素,桶元素在前缀(λ→1)中观察到的频率相似,以及对元素的特征相似性(λ→0)施加更大权重的哈希方案，因此,将目标中的第一项称为估计误差,将第二项称为相似性误差。

式(1)是一个非线性二元优化问题,很难解决，因此,下一步将提出不同的方法,用于在不同制度下求解最优解或接近最优的解。

2.2 混合整数线性格式

式(2)等价于下面的混合整数线性优化问题:

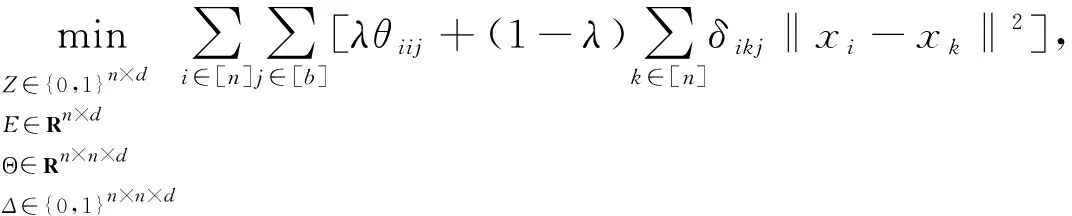
(3)

证明过程与文献[11]中定理1证明过程类似。

问题(3)由O(n2b)个变量和约束项组成。在本文所考虑的应用中,求解混合整数线性优化问题的计算量仍然是巨大的。为了解决该问题,本文提出了一种块坐标下降算法。

2.3 高效块坐标下降算法

通过利用问题(1)结构,提出了高效块坐标下降算法,该算法既可以启发式地解决问题(2),也可以用于计算问题(3)。

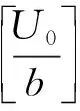
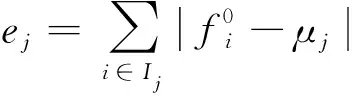
在每次迭代中,高效块坐标下降算法按顺序和随机顺序检查b个变量zi,i∈[n]的所有n个块,每个块包含特定元素到任何桶的所有可能的映射。对于每个元素i,选择较多映射值,使总体估计误差最小化。为此,将元素i从当前存储桶中移除,并计算与每个存储桶j相关的估计误差,将元素i分配到存储桶j,然后将元素i从存储桶j移除,将元素i分配到存储桶j*,使所有误差项的总和最小化。

当改进后的估计误差可以忽略时,算法终止;如果希望更快地获得中间解决方案,可以将终止标准设置为用户指定的最大迭代次数。经验表明,高效块坐标下降算法经过几十次迭代后收敛到局部最优,并得到性能较优的解。由于该算法不能保证收敛到全局最优解,因此该过程可以设置多组初始值,重复多次实验。

可以有效地实现高效块坐标下降算法,使每次迭代的复杂度为O(n2b)。这是意料之中的,因为对于每个桶,需要计算映射到其中的所有元素对之间的相似性错误,该过程的计算复杂度为O(n2b)。

2.4 动态规划算法

当λ=1的特殊情况下,即在计算最优哈希方案时,不考虑特征,可以得到以下公式:

(4)

式(4)是一个一维k中值聚类问题,根据文献[12],提出了一个复杂度为O(n2b)的动态规划算法解决问题(4)的最优性。在最优量化背景下,对问题(4)提出了一种更有效的求解方法;使用动态规划结合矩阵搜索技术,问题(4)的最优性的计算复杂度为O(nb)。

3 频率估计

3.1 前缀中元素的频率估计

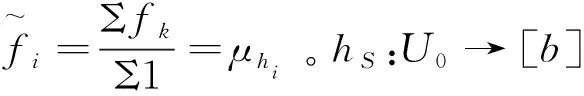
3.2 基于相似性的不可见元素频率估计

3.3 自适应计数扩展

上文描述了一种静态方法。学习流前缀中出现的元素的最佳哈希方案,然后只跟踪它们的频率,所有参数的估计频率仅基于U0中元素的频率。下文将描述一种动态方法,它跟踪U0中元素频率以外的元素频率。在较高的层次上,自适应方法基于对每个桶中不同元素的近似计数。工作步骤如下:

① 学习基于观察到的流前缀的最佳哈希方案,并训练将元素映射到桶的分类器,如上所述。对于每个桶,只记录其中映射的元素数量,而不是存储映射到此桶的元素的ID。使用分类器来确定任何元素映射到哪个桶。

② 在给定元素U和集合U′⊆U的情况下,针对所有元素u∈U或者u∈U′,进行概率测试,U′对应于流数据中出现的元素。如果u∈U′,那么Bloom过滤器BF(u)=1；如果u∉U′,那么就不需要BF(u)=0。

③ 根据元素u∈U0初始化Bloom过滤器。一方面,将所有元素u∈U0初始化为BF(u)=1；另一方面,可能将元素u∉U0初始化为BF(u)=0或BF(u)=1。

④ 对于在处理流前缀S0之后出现在流中的每个后续元素u,将其映射到桶j∈[b]使用经过训练的分类器。然后,使用Bloom过滤器测试是否已经找到u。如果BF(u)=0,则增加频率φj和桶j中的元素数cj,并令BF(u)=1；如果BF(u)=1,只增加频率φj。

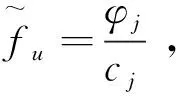
Bloom过滤器误报的影响是,本文方法将标记流中未出现的可见元素。当该元素出现在流中时,不会增加计数器cj,该计数器跟踪该元素映射的桶j中的元素数量，因此,j中元素cj的估计数量将小于实际数量，故而,自适应计数扩展通常会高估元素的频率。

4 有关合成数据的实验

4.1 数据合成

在合成实验中使用的数据是根据以下方法生成的:

元素:用一个正整数G∈Z>0参数化元素U的集合,通过下述方式控制问题大小。按指数递增2G0+1,2G0+2,…,2G0+G生成G组元素G1,G2,…,GG。将每组关联为Gg,g∈[G],具有p维正态分布,从[-10,10]p和等于恒等式的协方差矩阵中选择μg均值。绘制与每个元素u∈Gg相关联的特征,实现对应于元素组的p维正态分布N(μg,I)。

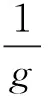
通过设置G=10和g0=0.5,得到了8 192个元素,其中只允许4 096个元素出现在前缀中,而前缀的大小为10 240，因此,目标是学习一种哈希方案。该方案最多将4 096个元素映射到10个桶，这种哈希方案的内存要求是约等于20 000 B。

4.2 实验软件配置

所有算法都采用Python 3编译器,运行所有实验的硬件配置为CentOS 7版的标准Intel(R)Xeon(R)CPU E5-2690@2.90 GHz。独立重复每个实验10次,并计算平均误差及其标准偏差。

优化算法如下:

MILP:使用商业MIO解算器Gurobi解决混合整数线性优化问题。

BCD:块坐标下降算法。

DP:通过动态编程在线性时间内解决问题。

本文研究的机器学习算法包括线性分类器,即多项式逻辑回归(Logreg)[13],基于树的分类器(Cart)[14],以及集成分类器,即随机森林(Rf)[15]。所有方法均使用10倍交叉验证进行调整;调整的超参数是Logreg正则化项的权重、Cart的最小杂质减少量和最大深度、每个分割中的最大特征数和rf的最大深度。在实验中使用Cart作为底层分类器,使用Scikit机器学习包实现上述所有算法。

将标准分钟示意图(CMS)称为计数分钟,将学习分钟示意图(LCMS)称为Heavy-hitter,使用Python实现了上述估计器。

4.3 结果分析

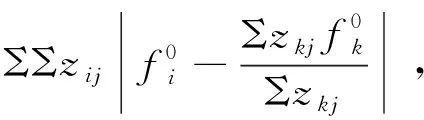
实验1超参数λ的影响。在本实验中,研究了超参数λ对学习哈希方案的影响。通过令G=6,并根据不同的λ,运行3个不同版本的哈希优化算法。记录前缀上的估计、相似性和总体误差,以及每个算法的运行时间。为了检验BCD的次优度,给出了构成目标函数误差项的实际值,也就是说,不以每元素或者每对元素的尺度进行转换。结果如图1所示。

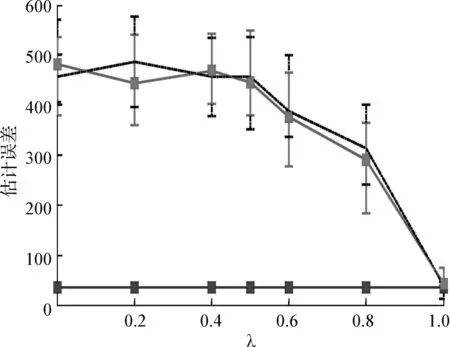
(a) 估计误差

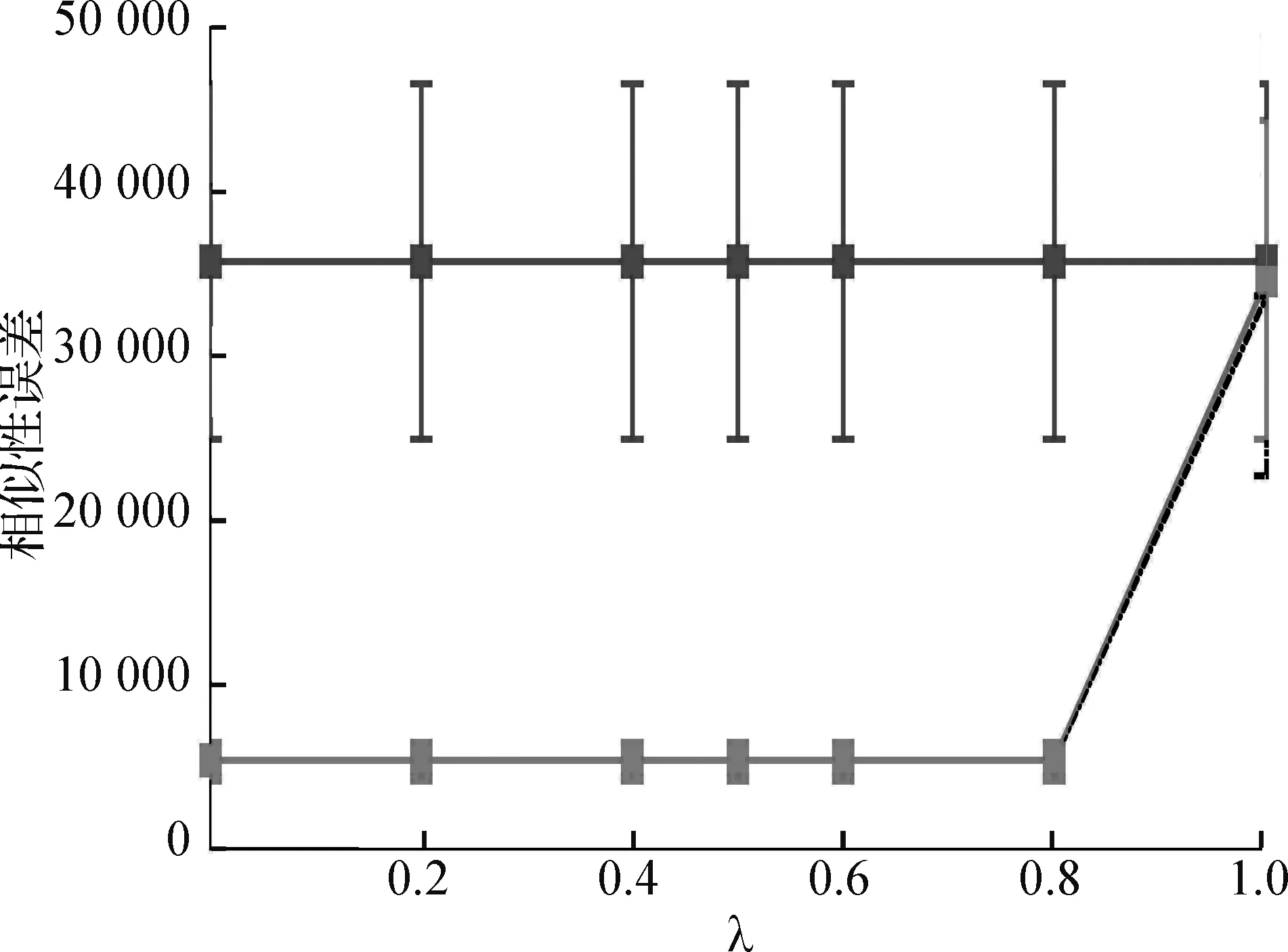
(b) 相似性误差

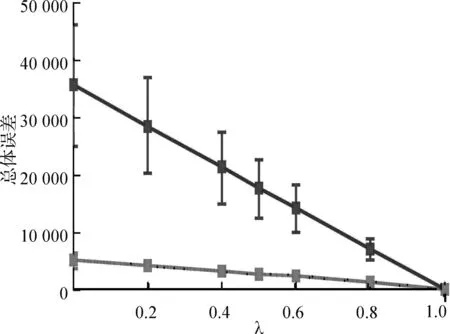
(c) 总体误差

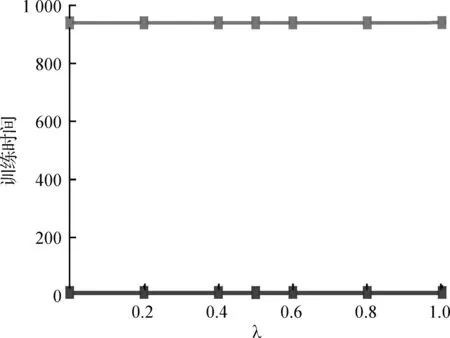
(d) 训练时间

图1 超参数的影响Fig.1 Effect of super parameters

从实验1结果可知:

MILP以增加运行时间为代价获得最小的总体误差。该方法相较于BCD方法更加优越,因为该方法得到的解几乎总比BCD获得的解更好。

BCD获得的解的时间性能较高;对于小规模的问题,BCD的运行时间1 s。

正如预期的那样,DP的估计误差最小,因为它仅针对与λ值无关的估计误差进行优化。但是就相似性和总体而言,DP的性能明显较差。

在λ=1的情况下,所有3种方法都能够找到可比较的近似最优解。

实验2λ=1时,BCD和DP之间的比较。在本实验中,将重点研究λ=1的情况,并比较G、BCD和DP的增加值。在这种情况下,后者可以保证找到最优的哈希方案。再次记录前缀上的估计、相似性和总体误差,以及每个算法的运行时间。在本实验和随后的实验中,以每元素与每对元素的比例转换误差,结果如图2所示。从图中可以观察到,对于G≤10的问题,BCD可以快速计算近似最优解;然而,随着G值的进一步增加,BCD的性能恶化。

(a) 估计误差

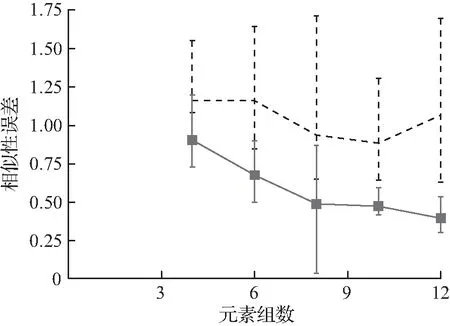
(b) 相似性误差

(c) 总体误差

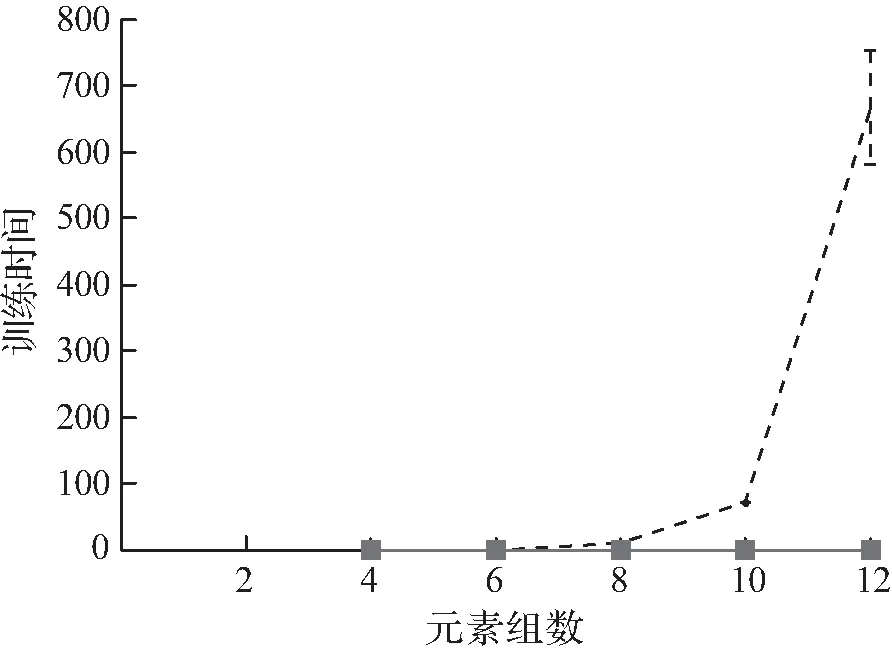
(d) 训练时间

图2 元素组数的影响Fig.2 Influence of element group number

实验3前缀中元素分数的影响如图3所示。在这个实验中,设G=10并改变g0的值,g0控制前缀中出现的元素的分数。探索了2种学习哈希方案的方法:首先,设置λ=0.5并运行BCD;然后,运行DP(λ=1)。记录前缀S0、元素上的估计和相似性错误,这些元素没有出现在S0中,但出现在S0之后的|S|=10|S0|。图3表明,在前缀中观察更多的元素会减少可见和不可见元素的估计误差,但会增加相似性误差。

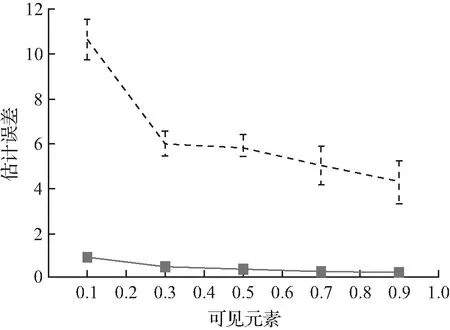
(a) S0估计误差

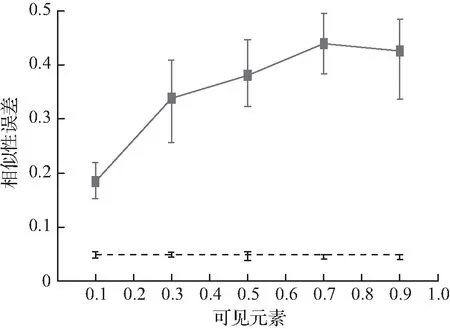
(b) S0相似性误差

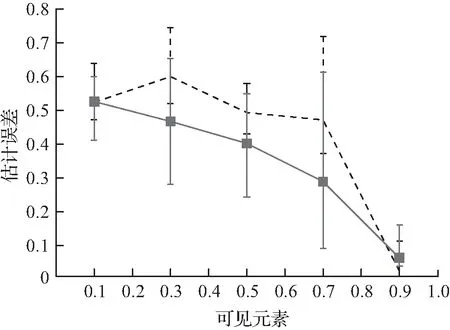
(c) |S|=10|S0|估计误差

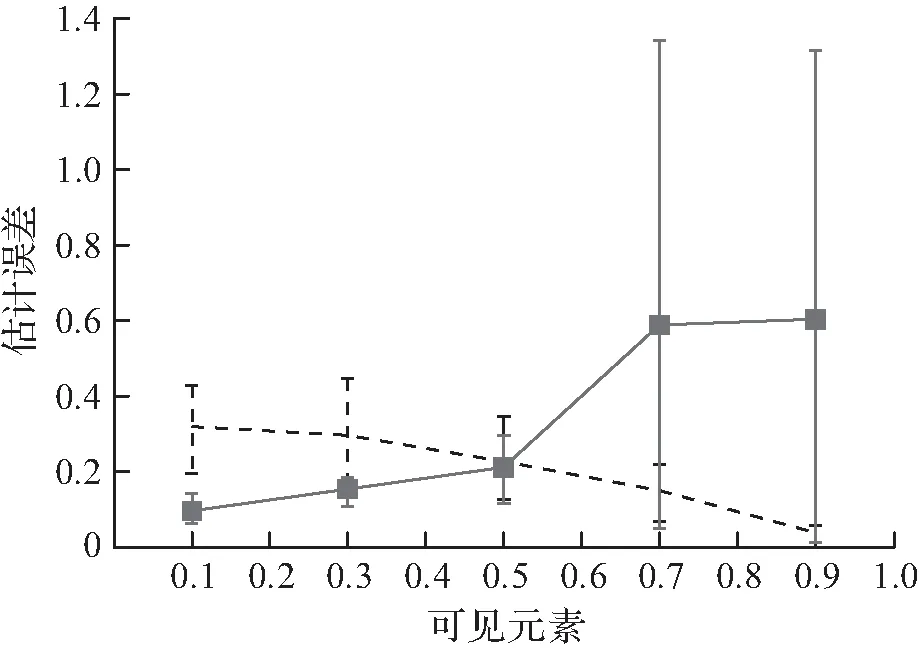
(d) |S|=10|S0|相似性误差

图3 可见元素的影响Fig.3 Influence of visible elements

实验4不同分类器的对比结果如图4所示。在这个实验中,设g0=0.33和λ=0.5,改变G的值,并探索使用不同类型的分类器(Logreg,Cart,Rf)作为哈希优化的一部分的影响。记录了S0中未出现但在S0后|S|=10|S0|到达范围内出现的元素的估计、相似性和总体误差,统计了每种方法的训练时间。在图中,可以看到使用非线性分类器的优点，然而,实验结果很大程度上取决于数据生成过程。

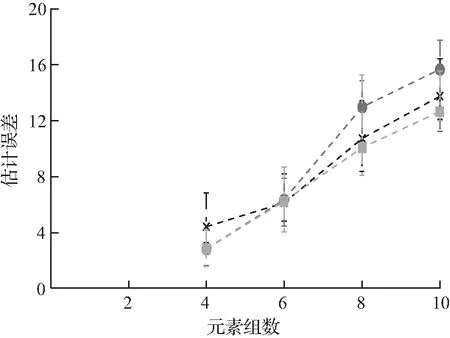
(a) 估计误差

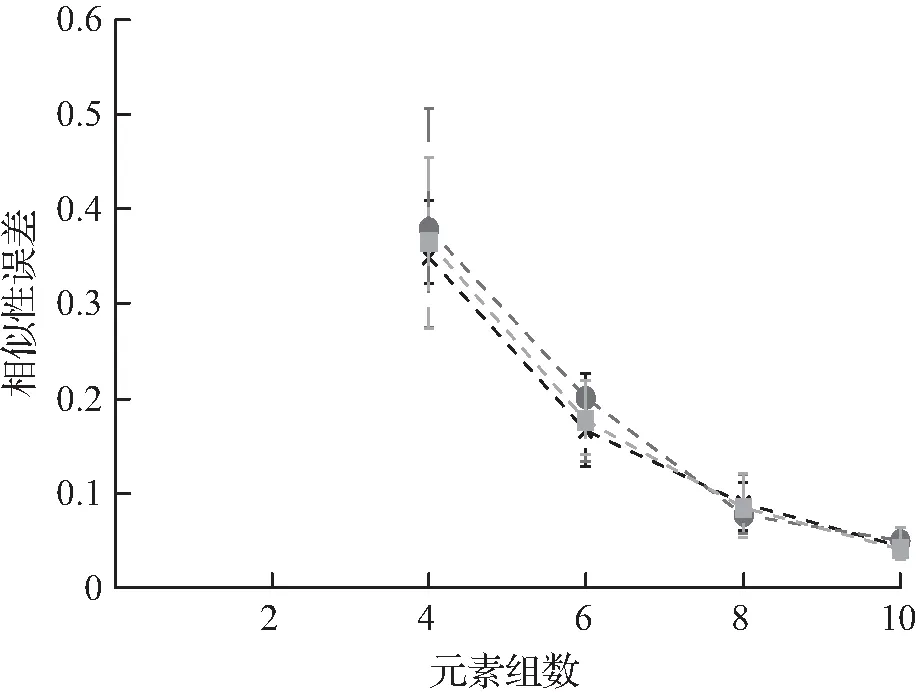
(b) 相似性误差

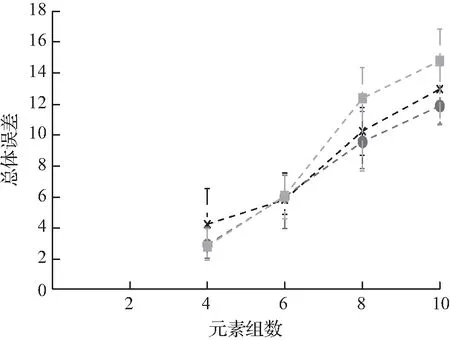
(c) 总体误差

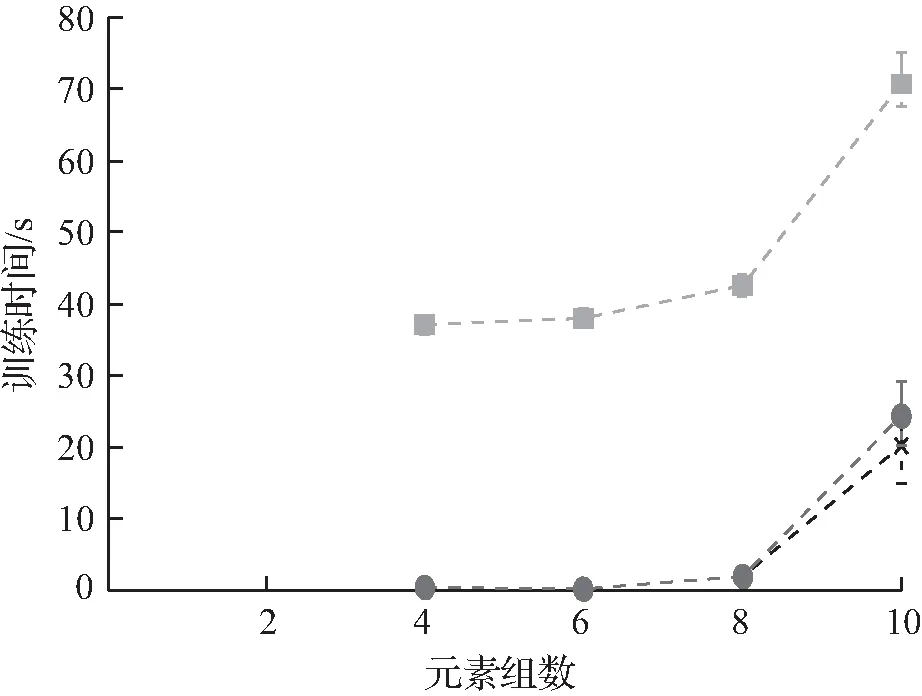
(d) 训练时间

图4 不同分类器的对比结果Fig.4 Comparison results of different classifiers

5 搜索查询估计

5.1 数据集

使用AOL查询日志数据集,该数据集包含2006年90 d内从65万匿名用户收集的2 100万个搜索查询,其中有380万个唯一查询。每个查询都是自由文本中的搜索短语,例如,第一个最常见的查询是“google”,在整个90 d内出现251 463次,第10个是“www.yahoo.com”,出现频率为37 436次,第100个是“mys”,出现频率为5 237次,第1 000个是“sharon stone”,出现频率为926次,第10 000个是“online casino”,出现频率为146次等。搜索查询频率的分布遵循Zipfian定律,因此该设置非常适合提出的算法(LCMS)。

5.2 基线方法

本文使用Count-min和Heavy-hitter作为基线方法。对于固定参数尺寸,即桶的总数b,统计了深度取d∈{1, 2, 4, 6}时的Count-min最佳性能,桶数量取bheavy∈{10,102,103,104}时的Heavy-hitter的最佳性能。此外,假设测试集中Heavy-hitter的ID是已知的，因此,将提出的方法与文献[10]中提出方法进行了比较。

5.3 提出方法

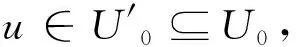
第一天包括超过20万个唯一的查询,仅存储它们的ID就需要20万个存储桶，因此,随机抽样观察到的查询子集,概率与观察到的频率成正比。使用查询的抽样子集作为本算法的输入。

对于固定数量的桶总数btotal,需要确定学习的哈希方案包含的桶数量b与将存储其ID的查询数量n之间的比率c，因此,对于用户指定的btotal和c,根据n=btotal/(1+c)和b=btotal-n选择b和n。在本文实验中,检验了c∈{0.03,0.3}时的模型性能。

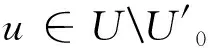
为了为分类器g创建输入特征,在训练查询中只保留500个最常见的词。还包括查询文本中ASCII字符的数量、标点符号的数量、点的数量和空格的数量。

5.4 结果分析

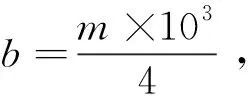
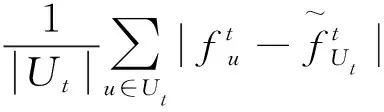
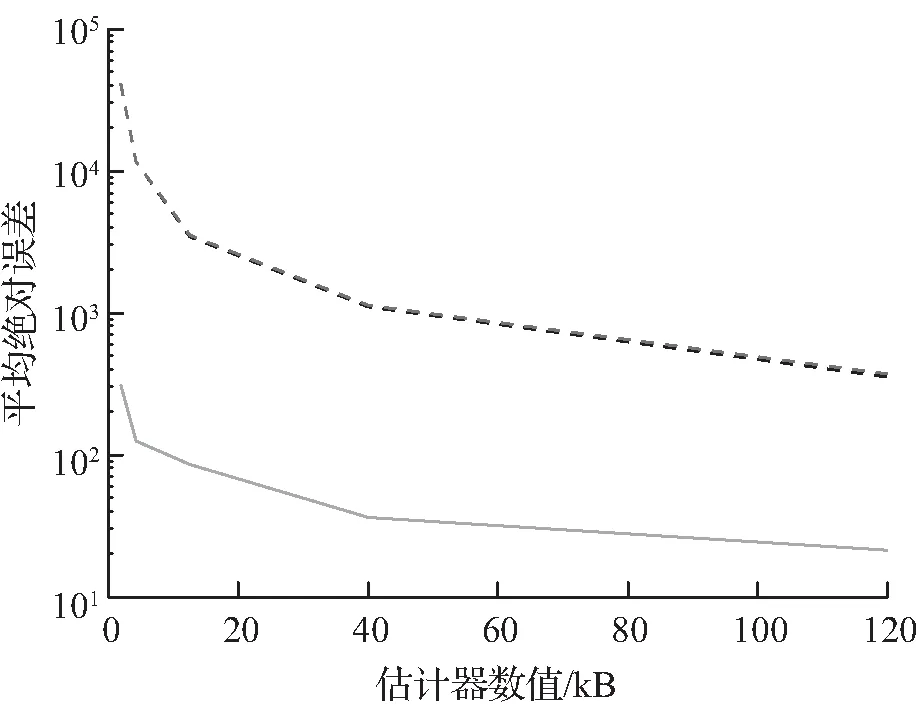
(a) 第30天平均绝对误差

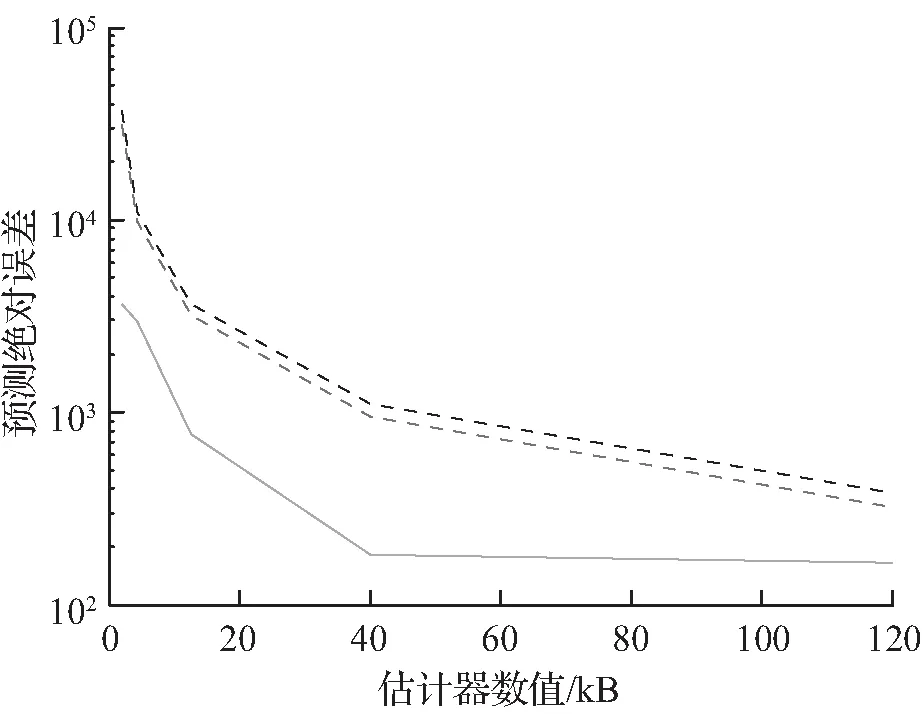
(b) 第30天预测绝对误差

(c) 第70天平均绝对误差

(d) 第70天预测绝对误差

实验中观察到,在第30、70天之后,估计误差的趋势非常相似。变化的是估计误差的绝对值,正如预期的那样,估计误差随时间而恶化,对所有方法都是一致的。所提出的方法在这2个指标上都优于其他比较方法,随着所有估计量的增加,它们的误差也会下降。

在平均误差方面提出方法性能表现最佳，原因是提出方法较适合估计很少出现的查询的频率。特别是,出现次数很少的查询被放在同一个桶中,因此它们的估计误差很小。相比之下,Heavy-hitter和Count-min通常将此类查询与中等或甚至高频率的查询放在同一个桶中,这会产生较大的估计误差。

当估计器的大小变得足够大时,Heavy-hitter和Count-min的估计误差的预期值似乎缓慢地收敛到提出方法估计误差，表明提出方法特别适合于低空间区域,并且可以实现更有效的频率向量压缩。

就Heavy-hitter和Count-min而言,前者确实产生了更好的估计,与文献[10]中的结果一致。就估计误差的预期值而言,改进更为显著。鉴于Heavy-hitter在出现频率最高的元素上没有错误,该观察结果也是可以预期的,这些元素在该度量中权重很大。

2种不同内存配置的估计误差随时间的变化如图6所示。从这2个指标来看,提出方法的优势随着时间的推移而保持。此外,观察到提出方法的估计误差达到最小的标准差，原因是元素到桶的映射比Heavy-hitter和Count-min的映射更稳定,因为它们是通过优化得到的,而不是通过随机化获得的,提出方法随机性的主要来源是分类器。

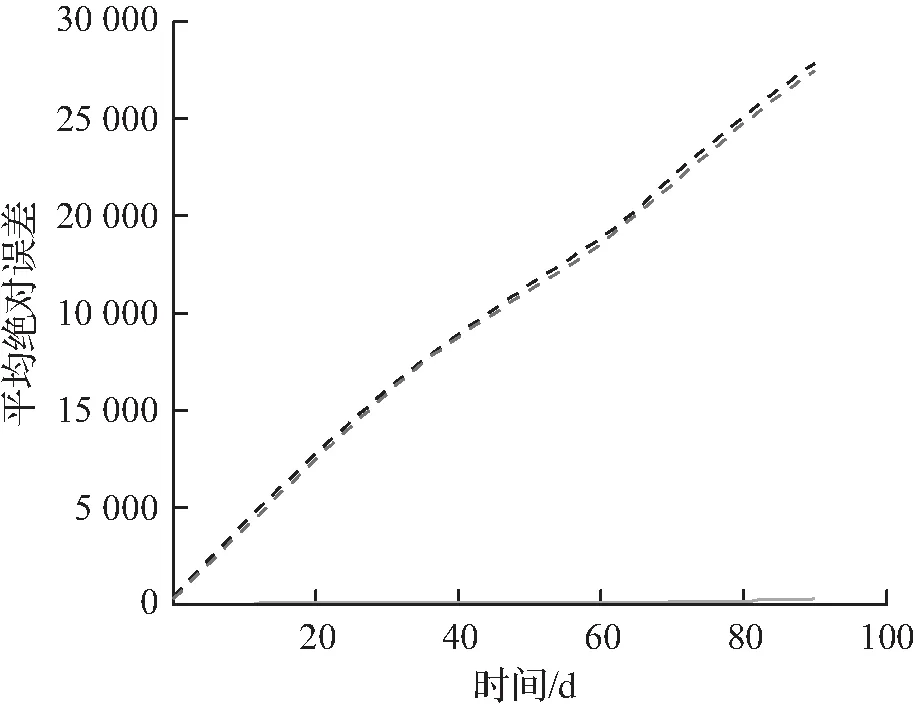
(a) 4 kB平均绝对误差

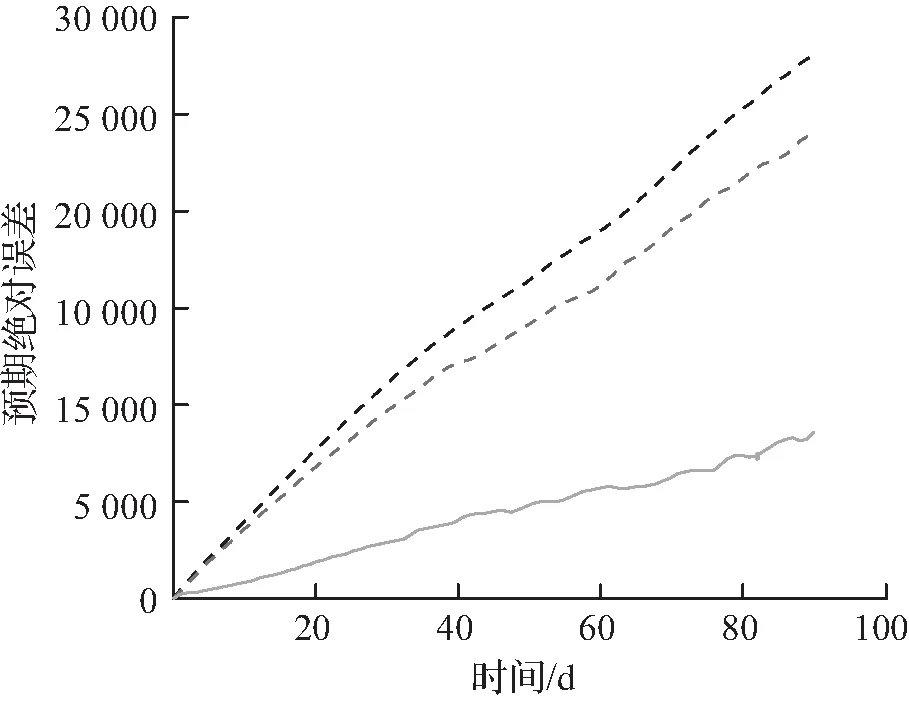
(b) 4 kB预测绝对误差

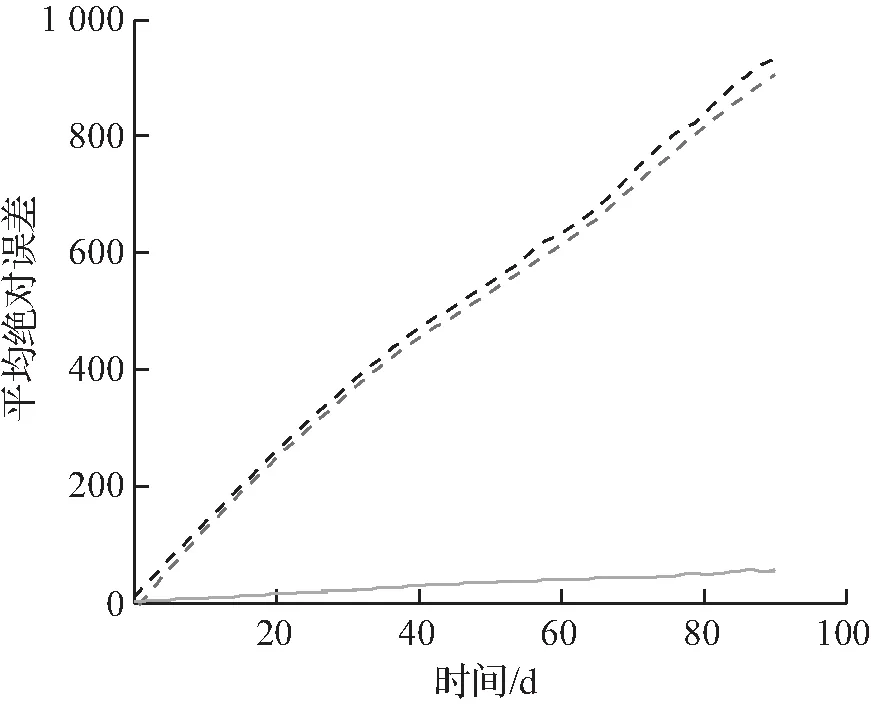
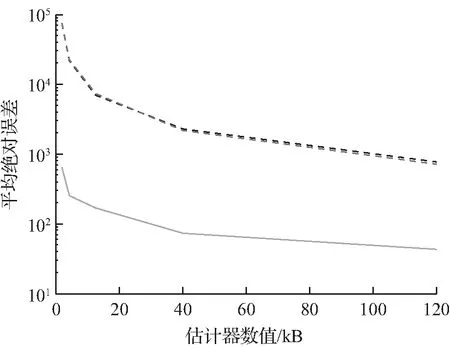
(c) 120 kB平均绝对误差

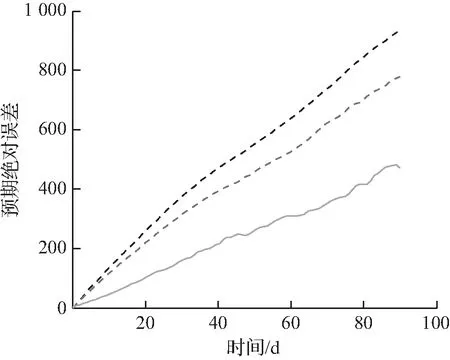
(d) 120 kB预测绝对误差

然后对1.2～120 kB的内存配置进行实验,并将提出方法与Count-min和Heavy-hitter进行比较。对于120 kB的内存,提出方法估计每个查询的频率的平均绝对估计误差大约为29,而Heavy-hitter的误差大约是479,如图6(a)所示。内存为4 kB时,提出方法和Heavy-hitter的误差大约分别为167和14 661,如图6(c)所示。表1统计了90 d内,1、10、100、1 000、10 000个最常见查询的平均误差占每个查询频率的比例。

提出方法的另一个特性是在机器学习元素中的可解释性,它可以深入了解潜在的频率估计问题。始终被标记为最重要的特征是4个变量,即查询文本中ASCII字符的数量、标点符号的数量、点的数量和空格的数量,以及单词“com”、“www”、“google”和“yahoo”,这一结果是合理的。

表1 平均误差百分比

6 结语

为了不依赖于随机哈希,并且降低计算复杂度,本文提出了一种基于块坐标下降算法的优化哈希数据流频率估计方法。所提出的算法使用混合整数线性优化动态规划方法,计算具有数千个元素的问题的最优哈希方案,以及使用块坐标描述算法计算具有数万个元素的频率估计问题。在合成数据集和搜索查询数据集上对所提出的方法进行了实验评估,实验结果证明:

① 提出方法能够不依赖于随机哈希实现频率向量的更新压缩,并跟踪所有元素的频率,与现有的流频估计算法相比,所提出的基于学习的流频估计算法具有更好的性能。

② 提出方法特别适合于低空间区域,并且可以实现更有效的频率向量压缩,另外提出方法较适合估计很少出现的查询的频率,其估计优势也会随着时间的推移而保持。

③ 提出方法在机器学习元素中具有较强的可解释性,它可以深入了解潜在的频率估计问题。