光晶格中多体极化子在Mott绝缘体区域的量子相

方家瑞， 殷 涛， 贺 亮*

(1. 华南师范大学物理与电信工程学院， 广州 510006； 2. 深圳市云韬量子科技有限公司， 深圳 518000)

光晶格中的冷原子体系一直是凝聚态物理的研究热点。它为研究量子多体系统提供了一个具有良好操控性的实验平台，是量子模拟[1]的最佳实验体系之一。近年来，超冷量子气体系统常被用于研究各种准粒子的物理性质[2,3]，极化子即为其中的一个研究对象。在固体物理中，极化子的最初定义是能带电子与光学格波声子相互作用形成的准粒子。在实际的研究工作中，原子与声子耦合之后形成的准粒子也被称为极化子。人们可以利用非平衡的玻色子-费米子混合体系[4]和费米子-费米子混合体系[5]研究原子类的极化子。在合适的参数条件下，很多实验体系[6-8]均可观测极化现象，比如原子之间通过原子-声子耦合诱导而来的长程相互作用。此外，通过偶极分子晶体[9]，纳米粒子[10]和混合原子-离子耦合体系[11]同样能实现原子-声子的耦合，观测到极化效应。研究极化子体系，有助于人们了解离子晶体和极性半导体的物理性质，同时在新一代量子器件的开发方面，这些研究工作也具有良好的应用前景。

随着实验技术的发展，极化子体系的粒子组份并不仅限于一种[12]。然而在相关的研究工作中[4-8]，极化子的种类一般只有1种，少有关于多组份极化子体系的讨论。本文研究光晶格中的多体极化子在 Mott绝缘体区域的系统性质，包括单组份和双组份的极化子体系。首先通过严格求解得到了二维光晶格中的单组份极化子在深Mott绝缘体区域下的量子相，包括极化子的填充数为1/2和1/4的2种情况。进一步地，利用Hartree-Fock平均场近似计算得到深Mott绝缘体区域下的双组份极化子在填充数分别为1/2和1/4时体系的量子相。

1 模型与方法

考虑有2种组份的玻色子分布在由第三种玻色子形成的玻色-爱因斯坦凝聚(BEC)的背景下，对应的粒子质量分别为m1、m2和mB，2种玻色子被激光束缚在二维光晶格中。

晶格中的玻色子本身具备动能，同时存在相互作用，这一部分的系统性质可以用2组份的玻色-哈伯德模型来描述，对应的哈密顿量HI为：

(1)

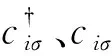
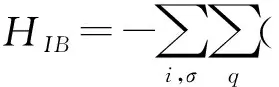
h.c.，

(2)

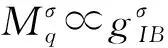
(3)

(4)

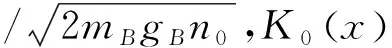
在深Mott体区域，哈密顿量式(3)中极化子的跃迁能一项可以忽略不计。对于极化子在空间分布的所有结构，系统的能量都可以通过式(3)严格求解。因此，可以通过数值求解所有分布状态对应的系统能量，其中最小的能量对应的情况就是系统基态下的粒子分布。在粒子填充数较小的情况下，利用上述方法可以简便有效地得到系统的量子相。当粒子填充数变大时，体系对应的希尔伯特空间维度随填充数指数增长，遍历所有构型求解体系基态的方法费时费力，可采用Hartree-Fock平均场近似式[17]

niσ1njσ2≈〈niσ1〉njσ2+niσ1〈njσ2〉-〈niσ1〉〈njσ2〉

(5)

处理极化子之间的长程相互作用项。在研究单组份极化子体系时，本文利用哈密顿量式(3)遍历所有构型直接求解体系基态；对于含有双组份极化子的体系，则利用Hartree-Fock平均场近似简化模型之后，再求解体系的量子相。

2 结果与讨论

2.1 平均场近似下的有效哈密顿量

利用式(5)将不同格点极化子相互作用按距离从最近邻、次近邻、次次近邻等依次展开：

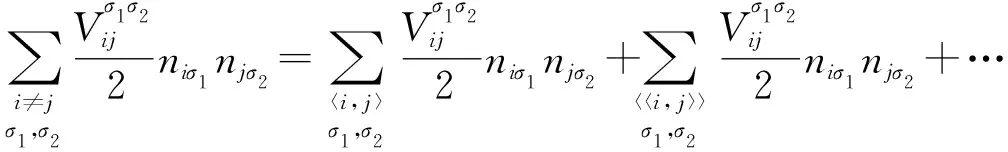
(6)

其中，常数项C的定义为:

(7)

(8)

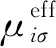
(9)

2.2 非平庸参数区域的讨论

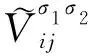
即总粒子数与总格点数的比值，其中符号〈ni〉表示对应算符的期望值，L是系统线性尺寸，本文取L=12，L2=144对应二维情况。不同组份的极化子数量保持一致，即ρb=ρd。在Mott绝缘体区域，系统更容易形成稳定的周期性结构，因此本文选择研究这一区域体系的量子相，包括只含有b组分和同时含有b、d这2种组份的极化子体系。

对于仅有b组份一种极化子的情况，能量

在系统的基态取最小值。体系基态可以通过遍历所有系统构型得到。对于含有b、d这2种极化子的系统，可以在满足E1最小的结构基础上，进一步求解使能量

取最小值的d组份极化子的分布结构。

2.3 极化子的系统结构

对于单、双组份的极化子体系，不同组份的极化子在晶格中的分布如图1和图2所示。

对于存在偶极排斥相互作用的单组份极化子体系，对应2种不同的填充数，系统都可以在整个空间上形成稳定的密度波结构。当填充数变小时，极化子之间的平均距离变大。因为偶极排斥作用使不同极化子趋于互相远离，但有限的系统尺寸使粒子之间不能无限远离，最终极化子形成图1所示的结构。

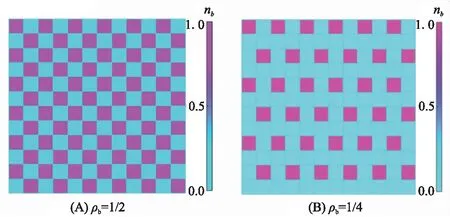
图1 不同填充数时b组份粒子随空间坐标的分布Figure 1 The particle distribution of b species in real space corresponding to different filling factors注：系统处于Mott绝缘体区域，系统线性尺寸L=12。

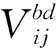
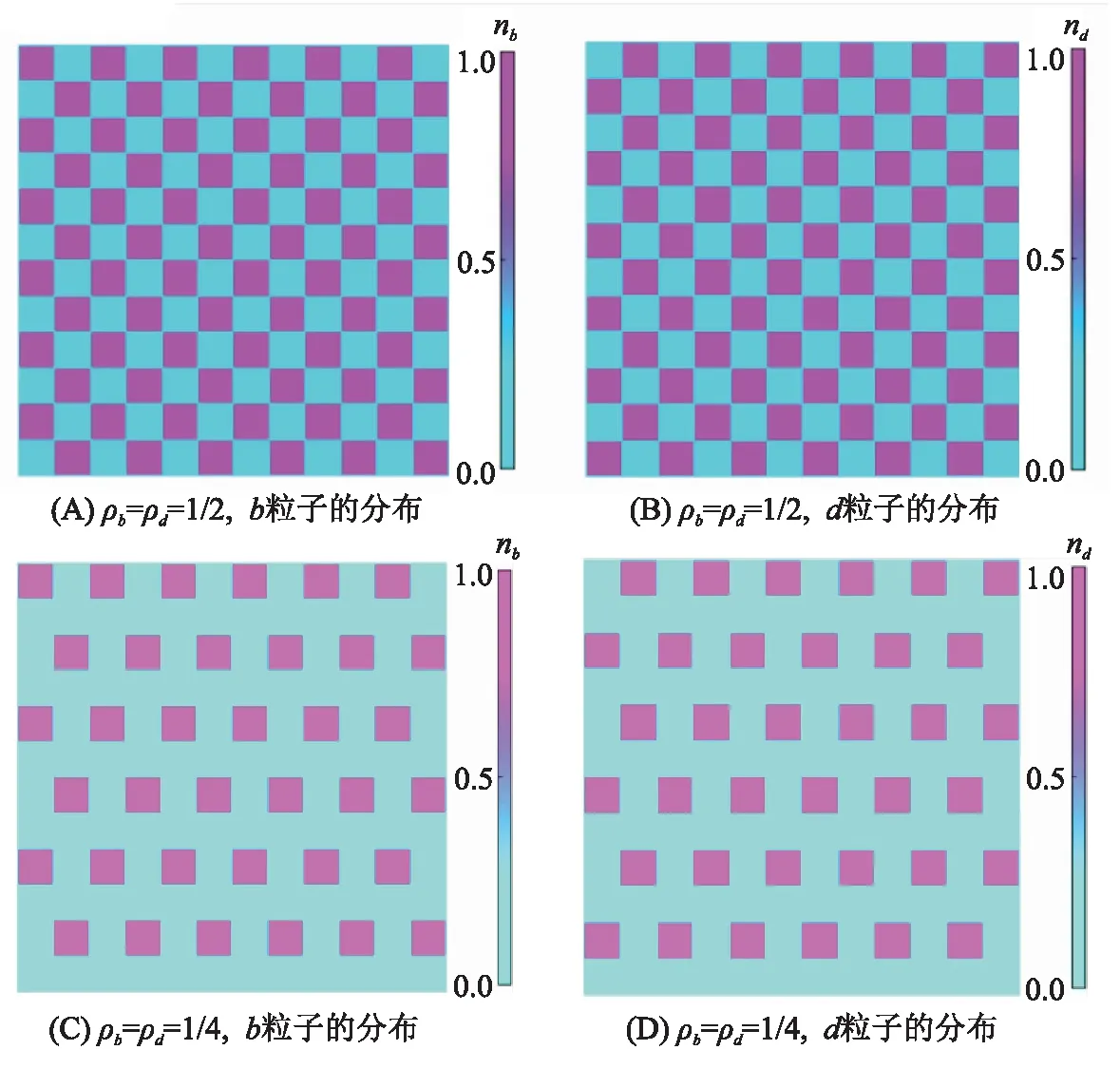
图2 不同填充数2组份极化子体系的量子相Figure 2 The quantum phases of the system with two-component polaron for different filling factors注：系统处于Mott绝缘体区域，系统线性尺寸L=12。

3 结论

研究了二维光晶格中的单组份和双组份极化子在Mott绝缘体区域的量子相。在BEC背景下，光晶格中的玻色子与BEC声子库存在耦合，形成准粒子(极化子)。极化子-极化子之间的相互作用可以通过Lang-Firsov变换得到，体系的有效哈密顿量形式为拓展的玻色-哈伯德模型。在考虑其中一种极化子本身存在偶极排斥相互作用的情况下，分别通过严格求解体系的有效哈密顿量和平均场近似的方法得到了单组份和双组份极化子在填充数分别为1/2和1/4时体系的量子相。结果表明：当系统处于Mott绝缘体相时，不同组份和填充数的极化子体系都能够在晶格中形成密度波。极化子之间的平均距离随填充数减少而增加；密度波的结构取决于极化子的填充数、组份以及玻色子与BEC声子之间的散射长度。

在后续的工作中，可以进一步研究体系随跃迁强度增大后从Mott绝缘体相到超流相的相变边界以及有限温情况下的系统性质。