玻色子体系的Bogoliubov变换*
白伊秀,胡 洁
(首都师范大学物理系,北京 100048)
0 引 言
在量子力学中[1],算符在不同表象中有不同的表现形式.当用矩阵表示算符时,如果取本征矢为基矢时,此算符矩阵为对角矩阵,当算符处于自身表象时,很多问题处理起来比较方便,如分析准粒子能谱、计算单分量玻色超流体系中的衰变率等[2-3].因此,需要将研究体系中的算符对角化到本征态下,对角化算符的过程称为幺正变换.在冷原子体系中,当研究低能物理中的玻色-爱因斯坦凝聚[4-6]、超流[4]和巴丁-库柏-徐瑞弗(Bardeen-Cooper-Schrieffer,BCS)超导态[7-9]时,需要做 Bogoliubov变换[10-12],使其从粒子数表象变成准粒子表象,而Bogoliubov变换的本质就是对角化平均场近似下的体系哈密顿量.进行Bogoliubov变换时需要考虑体系中的粒子是玻色子还是费米子,如果体系中的粒子为费米子,则哈密顿量的对角化按正常的幺正变换进行操作,但是若为玻色子,则不能做哈密顿量的幺正变换,即量子力学中的幺正变换只适用于费米子体系,而不适用于玻色子体系,其根本原因在于幺正变换是一个三角变换(sin2θ+cos2θ=1),满足反对易关系,而玻色子对角化是双曲变换(cosh2θsinh2θ=1),需满足对易关系,因此,不能直接用幺正变换,通常可以选择代数方法,在满足玻色子对易关系的条件下对角化哈密顿量,但是由于计算的复杂性,代数方法不利于推广到高维哈密顿量体系,因此,本文研究如何在玻色子体系中通过矩阵变换实现Bogoliubov变换.
1 费米子体系Bogoliubov变换
在研究玻色子体系之前,首先考虑一个自旋1/2、相互作用为接触势能的费米子体系,其二次量子化之后的哈密顿量为[13-15]

在Nambu表象中用矩阵表示此哈密顿量为


2 玻色子体系Bogoliubov变换
为了研究玻色子体系如何做Bogoliubov变换从而得到超流,考虑自旋为0、相互作用为接触势能的玻色子体系,其二次量子化之后的哈密顿量为[14]

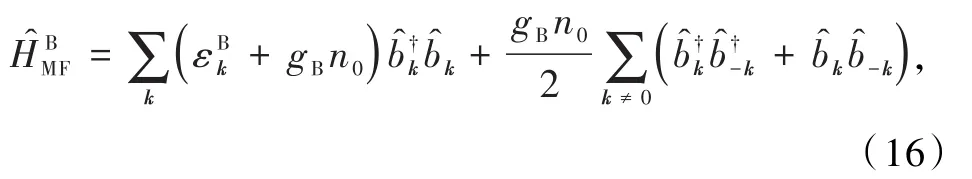
在Nambu表象下得
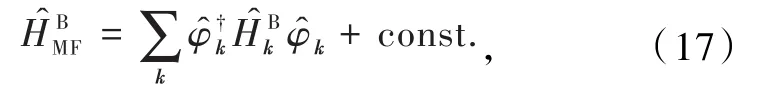
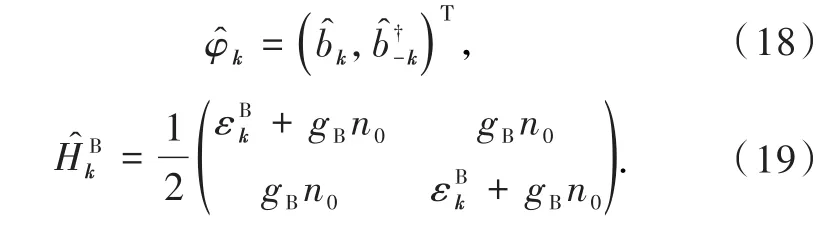
需要通过做Bogoliubov变换寻找本征表象,并且在本征表象下,哈密顿量矩阵是对角的.首先,按照费米子对角化的方式,尝试玻色子体系是否可以实现Bogoliubov变换,从而对角化玻色子哈密顿量.假设玻色子准粒子算符为k,变换矩阵为,则准粒子表象下的算符及哈密顿量与粒子数表象下的算符及哈密顿量的关系为准粒子算符需满足玻色子对易关系,即.但通过计 算式(26)可 知,,即用幺正变换来对角化无法满足玻色子对易关系.因此,通过幺正变换对玻色子体系做Bogoliubov变换的方法是不正确的.

通常可以用代数的方法,假设变换矩阵是普适的,在满足玻色子准粒子对易关系的情况下计算出每个矩阵元,但是当考虑高维玻色子体系时,如讨论自旋为1的玻色子时,需要对角化的是6×6的矩阵,若用代数方法对角化哈密顿量存在计算的复杂性.因此,需要找到可行的哈密顿量矩阵对角化方法,来实现Bogoliubov变换.本文构造如何对玻色子体系做矩阵变换来实现Bogoliubov变换.

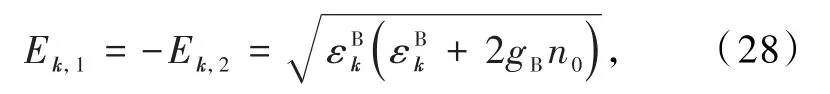
Ek,α对应的本征态为2,代表2个不同的本征态,而本征态的归一化关系为:
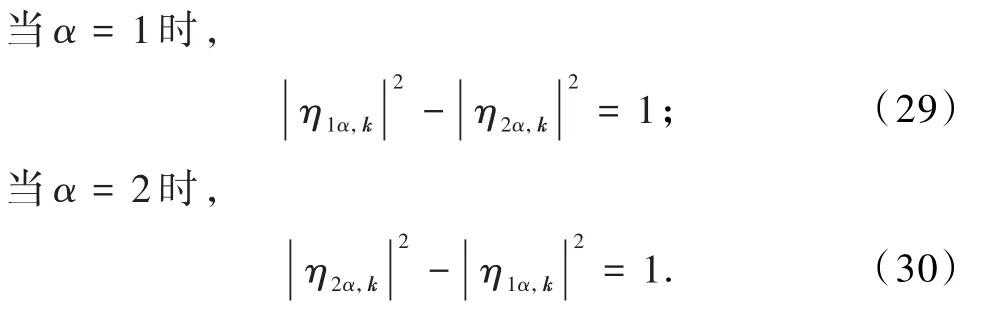
按照此归一化条件计算出本征态为

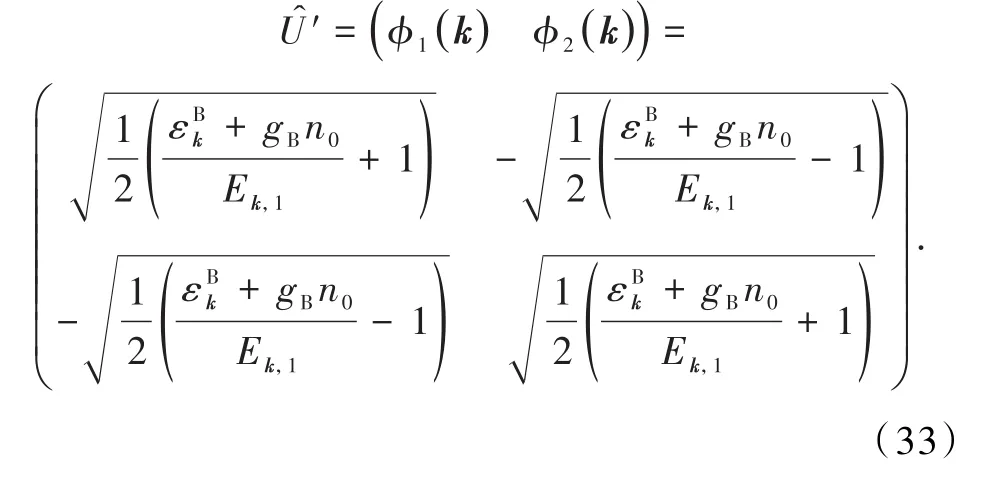

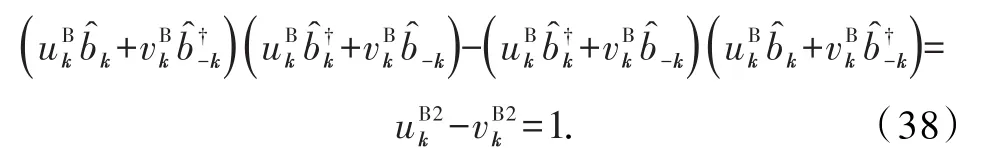
通过此变换矩阵不仅得到正确的超流能谱,还满足玻色子对易关系,并且对角化体系的哈密顿量.此方法还可以推广到高维体系,只需在Bk的偶数行乘以-1,得到新的哈密顿量′,再解′的久期方程,计算本征态时,本征值为正的本征态满足式(29)的归一化关系,本征值为负的本征态满足式(30)的归一化关系.
3 结 论
量子力学中幺正变换对角化哈密顿量得到的变换矩阵满足反对易关系,因此,适用于费米子体系.然而玻色子满足对易关系,幺正变换已不再适用.因此,本文研究了玻色子体系哈密顿量的对角化问题,为了满足对易关系,需要将哈密顿量的偶数行乘以-1,再计算久期方程,本征态的归一化条件也因本征值的正负不同而不同,最后将得到的本征态组成变换矩阵,而这个变换矩阵即可完成玻色子体系的Bogoliubov变换.需要说明的是,得到此变换矩阵的方法可以推广到高维体系,从而解决代数方法计算的复杂性.

