带有分数阶导数边值条件的分数阶微分方程正解的存在性
赵 微, 高 扬
(大庆师范学院数学科学学院, 大庆 163712)
近几十年来,分数阶微分方程及其边值问题受到了许多学者的关注,在很多科学领域中都有着广泛的应用。目前,关于分数阶微分方程边值问题的研究已经有很多成果[1-13],但是关于边值条件中带不同分数阶导数的研究相对较少。
薛益民等[1]运用Guo-Krasnosel’skii’s不动点定理,得到如下分数阶微分方程正解的存在性:
其中,Dα(2<α≤3)为Rimann-Liouvile分数阶导数。
张凯斌和陈鹏玉[3]运用非紧性测度的估计技巧与凝聚映射的不动点指数理论,得到如下分数阶微分方程正解的存在性:
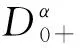
受文献[1]、[3]的启发,本文考虑如下带有分数阶导数边值条件的分数阶微分方程
(1)
其中,ηi(0,1),0<η1<η2<…<ηm-2<1,βi[0,∞)。需要指出的是,这里的边值条件中带有不同阶数的分数阶导数。
文中首先构建其格林函数,得到相应的相关性质;其次,运用凸泛函上的不动点指数定理来计算不动点指数,从而得到了方程(1)至少存在一个正解的结论;最后,通过一个例子来说明定理的具体应用。
1 预备知识
首先,给出一些必要的定义和引理,推导出相应的带有分数阶导数边值条件的分数阶微分方程的格林函数,并给出格林函数的一些性质;然后,将方程(1)转化为一个等价的积分方程。
定义1[6]函数y:(0,+∞)→的v>0阶Riemann-Liouville积分定义如下
其中,等式右边是在(0,+∞)上逐点定义的。
定义2[6]函数y:(0,+∞)→的v>0阶Riemann-Liouville微分定义如下
其中,等式右边是在(0,+∞)上逐点定义的,n=[α]+1。
引理1[6]假设uC(0,1)∩L[0,1],有v>0阶导数C(0,1)∩L[0,1],则
其中,Ci(i=1,2,…,N),N是大于或等于v的最小整数。
为下文叙述方便,现给出如下假设条件:
(H2)h:(0,1)→[0,∞)连续,h(t)不恒等于0。允许h(t)在t=0,1处奇异,且
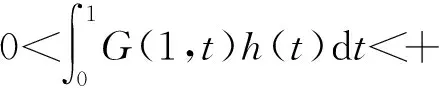
(2)
(H3)f:[0,1]×[0,+∞)→[0,+∞)连续。
引理2给定yC[0,1],边值问题
(3)
有唯一解
这里ηi(0,1),0<η1<η2<…<ηm-2<1,βi[0,∞),其中
证明应用引理1,将微分方程(3)转化为等价的积分方程
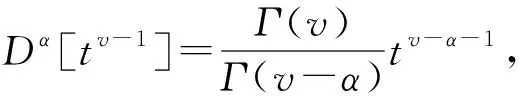
整理得
于是
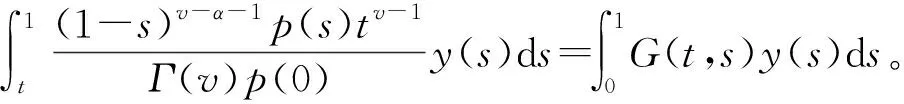
证毕。
引理3函数p(s)在[0,1]上单调不减且恒正。
证明因为
(1-s)αi-v(1-s)α-αi((v-αi-1)(1-s)+
((v-αi-1)(1-s)-(v-αi-1)(ηi-s)+
故p(s)单调不减。
又根据假设(H1)知,
从而知p(s)≥p(0)>0。证毕。
引理4函数G(t,s)具有如下性质:
(1)∀t,s[0,1],有G(t,s)≥0;
(2)∀t[0,1],有G(t,s)≤G(1,s);

证明(1)当0 当0 综上可知,∀t,s[0,1],有G(t,s)≥0。 (2)因为 所以,当0 综上可知,∀t[0,1],有所以G(t,s)关于t单调不减。因此,∀t[0,1],有G(t,s)≤G(1,s)。 (3)当1/4≤t≤3/4且0≤s≤t时,有 当1/4≤t≤3/4且0 证毕。 定义如下算子: (4) 接下来证明算子A的全连续性。 引理5设条件(H1)~(H3)满足,则算子A:P1→P1全连续。 证明由引理4可知 且 从而A:P1→P1,且A(P1)⊂P1。由Azela-Ascoli定理知, 算子A:P1→P1全连续。证毕。 下面介绍凸泛函的2个不动点指数引理。 定义3[14]对于锥P上的泛函ρ:P→,如果∀x,yP,t[0,1],满足 ρ(tx+(1-t)y)≤tρ(x)+(1-t)ρ(y), 则称ρ是锥P上的凸泛函。 引理6[14]设P是E中的锥,Ω是E中的有界开集,且θΩ。假设算子A:P∩→P全连续,ρ:P→[0,+∞)是凸泛函,且满足ρ(θ)=0,并对∀x≠θ,ρ(x)>0。 如果ρ(Ax)≤ρ(x),且当xP∩∂Ω时,Ax≠x,则不动点指数i(A,P∩Ω,P)=1。 (ii)ρ(Ax)≥ρ(x)且对∀xP∩∂Ω,Ax≠x, 则不动点指数i(A,P∩Ω,P)=0。 令 显然有h0≥hτ>0。 定理1假设条件(H1)~(H3)成立,s[0,1], 如果存在常数a和b, 使得当a,b>0时,有 (i)b 则带有分数阶导数边值条件的分数阶微分方程(1)至少存在一个正解。 证明令 则ρ1:P1→[0,+∞)是一致连续的凸泛函,且ρ1(θ)=0。 ∀uP1{θ},有 设Ω1={uC[0,1]|ρ1(u) 如果uP1∩1, 则 如果uP1∩∂Ω1,则ρ1(u)=b且因此 假设A在P1∩∂Ω1上没有不动点,则由引理6知 i(A,P1∩Ω1,P1)=1。 令 则ρ2:P1→[0,+∞)是一致连续的凸泛函,且ρ2(θ)=0,ρ2(u)>0(uP1θ)。 设Ω2={uC[0,1]|ρ2(u) 如果uP1∩2,则 如果uP1∩∂Ω2,则ρ2(u)=a且由于 所以 假设A在P1∩∂Ω2上没有不动点,由引理7知 i(A,P1∩Ω2,P1)=0。 ∀uP1∩1,有 定理2假设条件(H1)~(H3)成立,s[0,1],如果存在常数a和b,使得当0 则带有分数阶导数边值条件的分数阶微分方程(1)至少存在一个正解。 证明根据(i)有 设 显然有ρi:P1→[0,+∞)是一致连续凸泛函,且ρi(θ)=0(i=1,2)。 ∀uP1{θ},有 令Ω1={uC[0,1]|ρ2(u) 如果uP1∩1,则 如果uP1∩2,则 a≥ρ1(u)≥l‖u‖, 于是‖u‖≤al-1,这意味着P1∩Ω2是有界的。 假设A在P1∩∂Ω1和P1∩∂Ω2上没有不动点。如果uP1∩∂Ω1,则b=ρ2(u)≤‖u‖hτ,且 则 所以,由引理7知 i(A,P1∩Ω1,P1)=0。 如果uP1∩∂Ω2,则 由引理6知, i(A,P1∩Ω2,P1)=1。 综上可得 为了说明定理的应用性,下面给出一个具体的实例。 例1考虑如下的分数阶微分方程 (5) 且 取 有 0.001 6≤h0≤0.006 6,0.000 8≤hτ≤0.003 2。 综上可知,微分方程(5)满足定理1的3个条件,则该方程至少存在一个正解。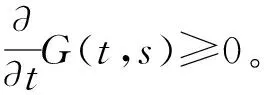
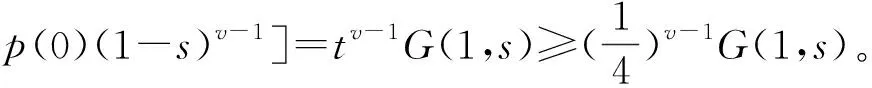
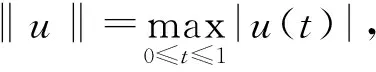
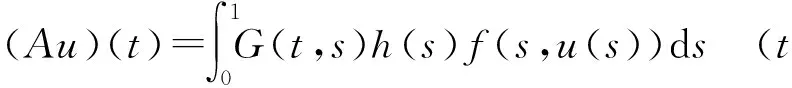


2 主要结论
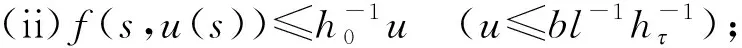
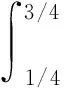
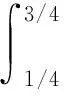

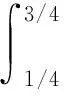
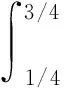
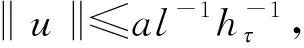
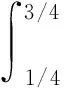
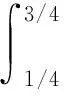
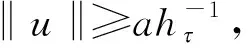


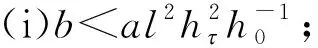
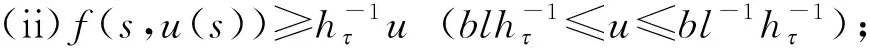
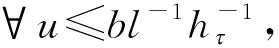
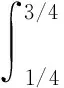
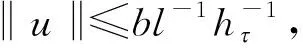

3 数值例子