完整内部安全的混合签密方案设计与分析

廖钰城， 王立斌， 黄杰彬

(华南师范大学计算机学院， 广州 510631)

签密方案(Signcryption Scheme,SC)[1]是一个逻辑步骤内同时实现数字签名和公钥加密功能的非对称密码协议，其在有效提高签名和加密效率的同时，还能够提供保密性、认证性和完整性等安全性保障，是公钥密码体制下确保网络环境中多方通信安全的重要密码技术。

混合签密方案(Hybrid Signcryption Scheme,HSC)是在传统签密方案的基础上，通过引入对称加密体制的协议构件来进一步提升了协议的计算效率，从而解决了传统签密方案在长明文通信时效率不佳的问题[2]。得益于此优势，近年所提出的签密方案[3-8]实质均为混合签密方案。为了方便实例化混合签密方案，BJØRSTAD和DENT[9]提出了带标签的签密密钥封装机制(Signcrytion tag Key Encapsulation Mechanism,SC-tag-KEM)，可通过“带标签的签密密钥封装机制+被动安全对称加密机制”(SC-tag-KEM+DEM)的构造来实例化混合签密方案。

混合签密方案的完整内部安全[10]是指在多方内部安全模型下，混合签密方案同时达到适应性选择密文不可区分性(IND-CCA2)安全和选择报文攻击强存在性不可伪造(SUF-CMA)安全。当前，许多研究致力于实现完整内部安全的混合签密方案[3-4,11]。2013年，LI等[11]基于签名后加密提出了一种签密方案，并声称其达到了完整内部安全，但实质上由于其未完整重用随机数，可通过解密后选取新鲜随机数重新加密的方式攻击其SUF-CMA安全，因此该方案并不具备完整内部安全。2014年，LU等[12]基于文献[11]实现了混合签密方案，但认证性上仅达到了存在性不可伪造(EUF-CMA)安全，未达到完整内部安全。2018年，GÉRARD和MERCKX[8]提出了基于格密码的后量子安全混合签密方案(SETLA)，但在加密算法设计上，误差分布的定义参数及误差参数均远超出既定限制范围，因此该协议不具备正确性。为解决上述正确性问题，刘镇等[13]放弃了随机数重用方式，提出了一种签名后加密的签密方案，但该方案仅能达到EUF-CMA安全，同样不具备完整内部安全。2019年，YANG等[14]提出了标准模型下的高效混合签密方案，但该方案的安全性仅达到了多方内部的IND-CCA2和EUF-CMA安全，无法达到完整内部安全。

为解决上述问题，本文主要基于SC-tag-KEM的通用构造，展开对完整内部安全的混合签密方案的相关研究。首先，提出了一种带标签的签密密钥封装机制(SC-tag-KEM)的通用构造方案(SCtKstd)，该方案通过数字签名构件绑定标签与密钥封装报文，进一步将得到的签名和临时密钥通过消息认证码进行外部信息绑定，从而在标准模型下可证明达到完整内部安全。然后，将SCtKstd方案应用在“SC-tag-KEM+DEM”的通用构造中，提出了可达完整内部安全的混合签密的通用构造方案(HSCstd)，并对其进行了安全性分析。

1 预备知识

下面对本文的符号进行说明，并列举方案构造以及分析中使用到的密码学原语。

1.1 符号说明

对于函数negl(n)，如果对于任意的正多项式p(·)，皆存在正整数N，使得对于任意的λ>N,皆有negl(n)<1/p(λ),则称negl(n)是可忽略函数。

1.2 密钥封装机制

密钥封装机制(Key Encapsulation Mechanism,KEM)由以下4个算法构成：

(1)KEMSetup(1λ)→prm：该算法以安全参数λ为输入，输出公共参数prm。

(2)KEMKeyGen(prm)→(pk,sk)：该算法以公共参数prm为输入，输出用户的公私密钥(pk,sk)。

(3)KEMEncap(prm,pk)→(K,C)：该算法输入公共参数prm和用户公钥pk，输出临时随机密钥K和对应该密钥的密钥封装报文C。

(4)KEMDecap(prm,sk,C)→Kor ⊥：该算法输入公共参数prm、用户私钥sk和密钥封装报文C，输出密钥K或错误信息⊥。

称密钥封装机制KEM有正确性，当且仅当对prm←KEMSetup(1λ)和任意(pk,sk)←KEMKeyGen(prm)、(K,C)←KEMEncap(prm,pk)，K=KEMDecap(prm,sk,C)以(1-negl(λ))的概率成立。

定义1[15](KEM的 IND-CCA2安全)称密钥封装机制KEM具备IND-CCA2安全，当且仅当对任意的概率性多项式时间攻击者，在KEM的协议环境下执行KEM的IND-CCA2安全游戏，获得游戏胜利的优势概率为：

且该优势概率关于安全参数λ可忽略。

1.3 数字签名

数字签名方案(SignatureScheme,SIG)由以下4个算法构成：

(1)SIGSetup(1λ)→prm：该算法以安全参数λ为输入，输出公共参数prm。

(2)SIGKeyGen(prm)→(pk,sk)：该算法以公共参数prm为输入，输出用户的公私密钥(pk,sk)。

(3)SIGSign(prm,sk,m)→σ：该算法输入公共参数prm、用户私钥sk和明文信息m，输出对应的数字签名信息σ。

(4)SIGVer(prm,pk,m,σ)→or ⊥：该算法输入公共参数prm、用户公钥pk、明文m和数字签名信息σ，输出接受信息或错误信息⊥。

称数字签名方案SIG具有正确性，当且仅当对prm←SIGSetup(1λ)和任意的(pk,sk)←SIGKeyGen(prm)及明文m，SIGVer(prm,pk,m,SIGSign(prm,sk,m))=成立的概率为(1-negl(λ))。

定义2[16](SIG的SUF-CMA安全)：称数字签名方案SIG具备SUF-CMA安全，当且仅当对任意的概率性多项式时间攻击者，在SIG的协议环境下执行数字签名的SUF-CMA安全游戏，获得游戏胜利的优势概率为：

∧(m′,σ′)]≤negl(λ)，

且该优势概率关于安全参数λ可忽略。

1.4 消息认证码

对称加密的消息认证码(Message Authentication Code,MAC)主要包含MACSign算法和MACVer算法。使用M表示消息认证码的对称密钥空间，该空间通常取决于安全参数λ。对任意的对称密钥mkM，明文消息τ{0,1}*，有MACVer(mk,σ=MACSign(mk,τ),τ)=以(1-negl(λ))的概率成立，称σ为明文消息τ关于对称密钥mk的消息认证码。

消息认证码的One-to-One属性：称消息认证码MAC是One-to-One的，当且仅当对任意的mkM，任意的明文消息τ{0,1}*，有且仅有唯一的消息认证码σ=MACSign(mk,τ)，满足MACVer(mk,σ,τ)=。

1.5 对称加密算法

(1)SYMENC(dk,m)→C：算法以对称密钥dkD和明文m为输入，输出密文C。

(2)SYMDEC(dk,C)→m：该算法以对称密钥dkD和密文C为输入,输出明文m。

称对称加密方案SYM具有正确性，当且仅当对任意的密钥dkD、明文m,m=SYMDEC(dk,SYMENC(dk,m))以(1-negl(λ))的概率成立。

定义3[17](对称加密算法的IND- PA安全)称对称加密方案SYM具备IND- PA安全，当且仅当对任意的概率性多项式时间攻击者，在SYM的协议环境下执行SYM的IND-PA安全游戏，获得游戏胜利的优势概率为：

且该优势概率关于安全参数λ可忽略。

1.6 密钥推导函数

D0={(dk,mk)|(dk,mk)←D×M},

D1={(dk,mk)K←K,(dk,mk)←KDF2(K)},

|Pr[b←{0,1},(dk,mk)←Db,b′←(KDF2,(dk,

mk)),b′]-1/2|≤negl(λ)

成立。

2 SCtKstd方案

本节将提出一种带标签的签密密钥封装机制的通用构造方案(SCtKstd)，并进行安全性分析。

2.1 带标签的签密密钥封装机制

带标签的签密密钥封装机制的协议概念[4]和安全模型[17]的具体表述如下。

定义4[4]带标签的签密密钥封装机制(SCtK)由以下6个算法构成：

(1)SCtKSetup(1λ)→prm：该算法以安全参数λ为输入，输出公共参数prm。

(2)SCtKKeyGenS(prm)→(pkS,skS)：该算法以公共参数prm为输入，输出用户的发送方公私密钥(pkS,skS)。

(3)SCtKKeyGenR(prm)→(pkR,skR)：该算法以公共参数prm为输入，输出用户的接收方公私密钥(pkR,skR)。

(4)SCtKSym(prm,skS,pkR)→(K,ω)：该算法输入公共参数prm、发送方私钥skS和接收方公钥pkR，输出临时随机密钥K和中间状态信息ω。

(5)SCtKEncap(prm,skS,pkR,ω,τ)→C：算法输入公共参数prm、发送方私钥skS、接收方公钥pkR、中间状态信息ω和标签信息τ，输出带标签的签密密钥封装报文C。

(6)SCtKDecap(prm,skR,pkS,C,τ)→Kor⊥：该算法输入公共参数prm、接收方私钥skR、发送方公钥pkS、签密密钥封装报文C和标签信息τ，输出密钥K或错误信息⊥。

称带标签的签密密钥封装机制SCtK具有正确性，当且仅当对任意的prm←SCtKSetup(1λ)、(pkS,skS)←SCtKKeyGenS(prm)、(pkR,skR)←SCtKKey-GenR(prm)、(K,ω)←SCtKSym(prm,skS,pkR)及C←SCtKEncap(prm,skS,pkR,ω,τ)，SCtKDecap(prm,skR,pkS,C,τ)=K以(1-negl(λ))的概率成立。

定义5[17](带标签的签密密钥封装机制的DM-IND-iCCA安全游戏)挑战者与攻击者按以下步骤进行安全游戏：

定义6[17](带标签的签密密钥封装机制的DM-IND-iCCA安全)称签密密钥封装机制SCtK具备DM-IND-iCCA安全，当且仅当对任意概率性多项式时间攻击者，在SCtK的协议环境下执行SC-tag-KEM的DM-IND-iCCA安全游戏，获得游戏胜利的优势概率为：

且该优势概率关于安全参数λ可忽略。

定义7[17](带标签的签密密钥封装机制的DM-SUF-iCMA安全游戏)挑战者与攻击者按以下步骤进行安全游戏：

定义8[17](带标签的签密密钥封装机制的DM-SUF-iCMA安全)称带标签的签密密钥封装机制SCtK具备DM-SUF-iCMA安全，当且仅当对任意的概率性多项式时间攻击者，在SCtK的协议环境下执行DM-SUF-iCMA安全游戏，获得游戏胜利的优势概率为：

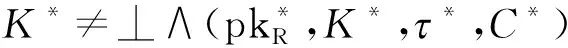
且该优势概率关于安全参数λ可忽略。

2.2 方案构造

定义密钥封装机制KEM=(KEMSetup,KEMKeyGen,KEMEncap,KEMDecap)，数字签名方案SIG=(SIGSetup,SIGSign,SIGVer)，信息认证码MAC=(MACSign,MACVer)，密钥推导函数KDF2:K→D×M，其中，K、D、M分别为KEM、DEM、MAC密钥空间。标准模型下，带标签的签密密钥封装机制的通用构造方案(SCtKstd)如图1所示。

图1 带标签的签密密钥封装机制的通用构造方案(SCtKstd)Figure1 The generic construction scheme (SCtKstd) of signcryption tag key encapsulation mechanism

2.3 安全性证明

定理1密钥封装机制KEM具备IND-CCA2安全，数字签名方案SIG具备SUF-CMA安全，密钥推导函数KDF2安全，信息认证码MAC满足一次选择信息攻击安全并具备One-to-One属性，则SCtKstd方案在标准模型下达到完整内部安全。

证明完整内部安全包含DM-IND-iCCA安全和DM-SUF-iCMA安全，以下从这2个方面给出SCtKstd方案的具体安全性证明，其中省略了协议内部的公共环境参数prm。

(1)SCtKstd方案的DM-IND-iCCA安全证明。假设存在攻击者以不可忽略的优势概率成功攻击SCtKstd方案的DM-IND-iCCA安全，考虑以下的一系列安全游戏：

除K的选取方式不同外，Game 0和Game 1完全一致。此时若存在攻击者，其在Game 0和Game 1中进行SC-tag-KEM的DM-IND-iCCA安全游戏的获胜优势分别为ε0和ε1，且获胜优势的差距是不可忽略的:|ε0-ε1|>negl()，则以攻击者为子算法,可构造区分器用于攻击KEM的IND-CCA2安全。

③进入DM-IND-iCCA安全游戏的阶段1。此时，攻击者将发起适应性查询(pkS,(C,σ1,σ2),τ)，要求返回SCtKDecap(skR,pkS,(C,σ1,σ2),τ)。

⑤进入DM-IND-iCCA安全游戏的挑战阶段。此时，攻击者发送给攻击者KEM。攻击者KEM根据其本身的挑战报文(pk,Kb,C*)，计算(dk0,mk*)=KDF2(Kb)，dk1←D，并随机抛币c{0,1}，将dkc返回给攻击者。在攻击者返回标签信息τ*后，攻击者KEM调用返回给攻击者。

因此，若密钥推导函数安全，则攻击者视角的Game 1和Game 2完全一致；否则,可构造区分器来区分该密钥推导函数的输出分布，从而得到：

最终可得到：

(2)SCtKstd方案的DM-SUF-iCMA安全证明。SCtKstd方案本质仍为加密后签名的结构，对于接收方内部敌手获取到的任意的签密报文((C,σ1,σ2),τ)，可通过对C解签密来获取对应σ2的MAC密钥mk。但在MAC的One-to-One属性情况下，若其成功构造出新鲜的合法签密报文来攻击DM-SUF-iCMA安全，则必然生成了新鲜的合法签名以此可攻击数字签名方案SIG的SUF-CMA安全。从而以攻击者为子算法，可构造对签名方案SIG的多项式时间攻击者SIG。

(3)进入DM-SUF-iCMA安全游戏的查询阶段。对攻击者适应性选取的接收方公钥pkR，攻击者SIG调用KMEncap(pkR)→(K,C)，生成(dk,mk)=KDF2(K)，设置中间状态信息ω=(mk,C)，返回dk给攻击者，并等待其后续查询。在接收到攻击者适应性选择的标签信息τ后，攻击者SIG根据标签信息τ、中间信息ω=(mk,C)和接收方公钥pkR，向挑战者SIG查询的签名信息σ1，并生成信息σ2=MACSign(mk,(σ1,pkS))，返回(C,σ1,σ2)给攻击者。

(4)进入DM-SUF-iCMA安全游戏的输出阶段。此时，攻击者输出针对SCtKstd方案的DM-SUF-iCMA安全的伪装报文攻击者SIG直接令将返回给挑战者SIG。

因此，在数字签名方案SIG本身具备SUF-CMA安全的情况下，SCtKstd方案是具备DM-SUF-iCMA安全的。

综上，SCtKstd方案在标准模型下可证明满足DM-IND-iCCA安全和DM-SUF-iCMA安全，进而达到完整内部安全。证毕。

3 HSCstd方案

本节将SCtKstd方案应用在“SC-tag-KEM+DEM”的通用构造当中，提出了一种可达完整内部安全的混合签密的通用构造方案(HSCstd)，并进行安全性分析。

定义9[9](签密方案，SC)完整的SC方案由以下5个算法构成：

(1)SCSetup(1λ)→prm：该算法以安全参数λ为输入，输出公共参数prm。

(2)SCKeyGenS(prm)→(pkS,skS)：该算法以公共参数prm为输入，输出用户的发送方公私密钥(pkS,skS)。

(3)SCKeyGenR(prm)→(pkR,skR)：该算法以公共参数prm为输入，输出用户的接收方公私密钥(pkR,skR)。

(4)SCSC(prm,skS,pkR,m)→C：该算法实现签密功能，输入公共参数prm、发送方私钥skS、接收方公钥pkR和明文m，输出签密密文C。

(5)SCUSC(prm,skR,pkS,C)→mor⊥：该算法实现解签密功能，输入公共参数prm、接收方私钥skR、发送方公钥pkS和签密密文C，输出明文m或错误信息⊥。

称签密方案SC具有正确性，当且仅当对prm←SCSetup(1λ)和任意的(pkS,skS)←SCKeyGenS(prm)，(pkR,skR)←SCKeyGenR(prm)，明文m和签密密文C←SCSC(prm,skS,pkR,m)，SCUSC(skR,pkS,prm,C)=m以(1-negl(λ))的概率成立。

3.1 通用构造方案

定义密钥封装机制KEM=(KEMSetup,KEMKey-Gen,KEMEncap,KEMDecap)，数字签名方案SIG=(SIGSetup,SIGKeyGen,SIGSign,SIGVer)，信息认证码MAC=(MACSign,MACVer)，对称加密算法SYM=(SYMENC,SYMDEC)，密钥推导函数KDF2:K→D×M，其中，D为临时密钥空间，M为MAC密钥空间。标准模型下，可达完整内部安全的混合签密的通用构造方案HSCstd如图2所示。

图2 可达完整内部安全的混合签密的通用构造方案(HSCstd)Figure 2 The generic construction scheme (HSCstd) of hybrid signatures with full insider security

3.2 安全性分析

HSCstd方案是基于文献[14]提出的混合签密通用构造方案，该方案的安全性基于定理1和以下引理。

引理1[9]若混合签密方案SC基于带标签的签密密钥封装机制SC-tag-KEM和数据封装机制DEM进行构造，并且SC-tag-KEM达到IND-CCA2安全，DEM达到IND-PA安全，则混合签密方案SC达到IND-CCA2安全。

引理2[9]若混合签密方案SC基于带标签的签密密钥封装机制SC-tag-KEM和数据封装机制DEM进行构造，且SC-tag-KEM达到SUF-CMA安全,则混合签密方案SC达到SUF-CMA安全。

因此，只需选取达到IND-CCA2安全和SUF-CMA安全的SC-tag-KEM以及满足IND-PA安全的DEM作为混合签密方案HSCstd的底层协议构件，根据定理1、引理1和引理2，即可证明HSCstd方案达到了完整内部安全。

4 结论

本文在不重用随机数的情况下提出了一种带标签的签密密钥封装机制的通用构造方案(SCtKstd)，该方案通过使用SIG构件绑定了标签和密钥的外部信息，在标准模型下达到完整内部安全。然后，结合SCtKstd方案与“SC-tag-KEM+ DEM”通用构造[9]，提出了可达完整内部安全的混合签密通用构造方案(HSCstd)，并进行了安全性分析。结果表明：HSCstd方案具备了多方内部安全模型下的IND-CCA2安全和SUF-CMA安全，进而达到了完整内部安全。同时，由于模块化构造时所使用的构件具有多种成熟的实现方案，使得HSCstd方案具备较好的通用性和实用性。

然而，相对于经典计算攻击者，量子攻击者不仅具有更强的计算能力，还具有更强的问询能力。SCtKstd方案在安全性证明时所使用的安全模型为Chiba[17]的动态多方内部安全模型，该模型并未考虑量子攻击者的量子叠加态问询能力，因此，SCtKstd方案也未被证明能有效抵抗量子攻击。所以，在后量子安全模型下来分析混合签密方案的安全性是下一步研究工作的重点。